Rep:Mod:Juan sheet does plenty

Module 3 - The Transition State

The Cope Rearrangement

The Cope rearrangement is a [3,3] sigmatropic pericyclic reaction which has been studied extensively both experimentally and computationally. It is now widely accepted that the reaction proceeds in a concerted manner whereby a single σ bond is broken and another is formed, the transition state is believed to take the form of either the "chair" (usually slightly more energetically favourable) or "boat" conformation.

[3,3] sigmatropic rearrangement of 1,5-Hexadiene

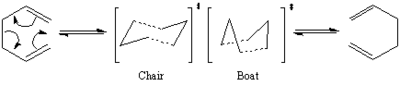
Previous modules have shown how molecular mechanics/force field methods can be used to accurately determine the energy and structure of the intended molecule. However this approach cannot be used when studying transition states since these methods do not take into account bond making and breaking processes, furthermore they are also unable to comprehend changes in electron distribution/bonding type. Consequently to accurately model the transition states a molecular-orbital based approach will be utilised whereby the Schrodinger equation will be solved numerically in order to locate transition structures based on the local shape of the potential energy surface. Knowledge of the structure (symmetry of the orbitals) and energy of the transition states is paramount when trying to understand a reaction mechanism since the mechanism depends on the correct overlap of orbitals with appropriate symmetry. Ultimately the intrinsic reaction coordinate (IRC) will be used to evaluate the structures of the reactant/product with that of the transition state.

Optimising the Reactants and Products

Optimisation with HF/3-21G

Several different conformers of 1,5-hexadiene were drawn in Gaussview. These structures were then optimised to the HF (Hartree-Fock approximation)/3-21G (basis set) level of theory, the total energy was found and given relative to the lowest energy conformation (found both from appendix 1 and by trial and error). The point group was also obtained using the symmetrise function. Originally 1,5-hexadiene was drawn with the four central carbon atoms in the anti linkage (approx a.p.p.) then optimised, different structures were tried including gauche arrangements. Each conformation was named according to their corresponding structures in appendix 1.

Conformers of 1,5-Hexadiene and their relative energies

Conformer		Energy (a.u.)	Relative Energy (kcal/mol)	Point Group
anti 1		-231.69260236	0.04	C2
anti 2		-231.69253528	0.08	Ci
gauche 1		-231.68771612	3.10	C2
gauche 3		-231.69266120	0.00	C1

Based on consideration of steric repulsions alone it would be expected that the anti conformations would be lowest in energy since the carbon atoms are as far apart as possible therefore reducing the steric repulsions. This is in fact the case on comparison of conformations anti 1/2 and gauche 1 since the overall energy is (more negative) than the corresponding gauche geometry. However this was not the case for the gauche 3 conformation which had the lowest overall energy. The reason this conformation is the most energetically favoured is because it benefits from a stabilising stereo electronic interaction of the C=C π electrons with the CH σ* orbital of the vinyl protons. This interaction is known as a CH-π overlap and partially accounts for the slightly lower energy of the gauche 3 conformation. Finally the gauche 3 conformer also may benefit from Van der Waals interactions between hydrogen atoms due to the close proximity in the gauche conformation compared to the anti forms of 1,5-hexadiene. The findings reported above are also in agreement with those found by Rocque et al.

Geometry Optimisation of Anti 2 conformer with DFT/B3LYP/6-31G(d)

The anti 2 conformation was re-optimised using the higher DFT/B3LYP/6-31G(d) level of theory. The resulting structure was compared to that obtained from the HF/3-21G method.DOI:10042/to-8035

Comparison of bond angles and lengths in optimised structures of the anti 2 conformer

Property	1st Opt (HF/3-21G)	2nd Opt (B3LYP/6-31G*)
Energy (a.u.)	-231.69253528	-234.61171951
Point Group	Ci	Ci
Dihedral Angle (o): C1-C4-C6-C9	114.7	118.5
Bond Angle (o): C1-C4-C6	124.8	125.3
Bond Angle (o): C4-C6-C9	111.3	112.7
Bond length (Å): C1=C4	1.32	1.33
Bond Length (Å): C4-C6	1.51	1.50
Bond Length (Å): C6-C9	1.55	1.55

As it can be seen from the table above the geometries of the conformers changes very little between the two optimisation methods. Although in the B3LYP/6-31G(d) method the overall energy was lower than that calculated in the HF/3-21G method. However the two energies should not really be compared since two different levels of theory were used in the calculations. The point group remained the same in both calculations and the only major difference between the two geometries lies in the bond angles. The largest difference between the two methods was in the calculation of the dihedral bond angle which was calculated to be 4^o larger in the DFT/B3LYP/6-31(d) level of theory method. In general all the bond angles calculated in the DFT method were larger than in the HF method, this could account for the slightly lower energy obtained from the DFT method due to minimisation of steric repulsions. However since both methods give very similar results it is difficult to say which method is the most accurate.

Vibrational Frequency Analysis

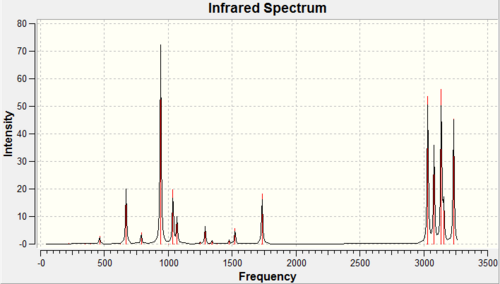
To confirm the optimised structure calculated from the DFT/B3LYP/6-31G(d) method was indeed a minimum on the potential energy surface a vibrational frequency analysis was performed. Since no negative (imaginary) frequencies were obtained this confirms that an energy minimum was found and not a transition state. DOI:10042/to-8010

Vibrations for Optimised Anti 2 Conformer

Frequency	Animation	Intensity	Description
1734		18	asymmetric C=C stretch
3031		54	symmetric C-H stretch
3081		36	asymmetric C-H stretch
3137		56	alkene C-H stretch
3156		15	alkene C-H stretch
3234		45	alkene C-H stretch

It should be noted that there is an error of around 10% associated with the calculation of the vibrational frequencies. This means in general the stretching frequencies are higher than expected, The reason for this large error is because the vibrations are treated as harmonic oscillations rather than using the more realistic anharmonic approximation.

Thermochemistry Analysis of Anti 2 Conformer

From the resulting output file of the vibrational frequency analysis of the anti 2 conformer the thermochemical data can be extracted. It should be noted that the vibrational energies, contributions and corrections are temperature dependant so can therefore be calculated at different temperatures.

Thermochemistry Analysis of Anti 2 Conformer

Energy	Value (298.15K) (a. u.)
Sum of electronic and zero-point Energies	-234.469196
Sum of electronic and thermal Energies	-234.461849
Sum of electronic and thermal Enthalpies	-234.460904
Sum of electronic and thermal Free Energies	-234.500779

The 'sum of electronic and zero point energies' is the potential energy at 0K which includes the zero-point energy (E = E_elec + ZPE). The 'sum of electronic and thermal energies' is the energy at 298.15 K and 1 atm of pressure which includes contributions from the translational, rotational, and vibrational energy modes (E = E + E_vib + E_rot + E_trans). The 'sum of electronic and thermal enthalpies' contains an additional correction for RT (H = E + RT), which is especially important when looking at dissociation reactions. The 'sum of electronic and thermal free energies' includes the entropic contribution to the free energy (G = H - TS).

Optimising the Chair and Boat Transition Structures

After optimising the reactants it was then time to optimise the transition state geometry, however the transition state exists in two different conformers (chair and boat). Initially using Gaussview a CH₂CHCH₂ fragment was drawn and optimised to the HF/3-21G level of theory. The resulting structure was then copied and pasted twice into a new window, arranging the fragments into a chair conformation so that the terminal carbon atoms were 2.2 Å apart. The structure obtained was then optimised in two different ways.

1. TS (Berny) method, which calculates the force constant matrix (Hessian) at the first step and then recalculates throughout the optimisation. However this method is very sensitive to the geometry of the input therefore it is essential that the structure used for the transition state is accurate in order to optimise the actual TS.

2. The frozen coordinate method, This method involves freezing the reaction coordinate and then minimising the rest of the molecule. Then the molecule is allowed to relax and the transition state is then re-optimised. Using this method has the additional bonus that the entire Hessian does not need to be calculated.

TS (Berny) Method

Using the drawn transition state (consisting of the two CH₂CHCH₂ fragments arranged in the chair conformation) an opt+freq calculation was performed. The options 'Optimise to a TS (Berny)' and 'calculate force constants once' were selected, also in the additional keywords section 'Opt=NoEigen' was added. The reason for this was to prevent the calculation from crashing if more than one imaginary (negative) frequency was calculated. From the resulting output file a single imaginary frequency was calculated, this was found to be at -818cm^-1 (which is in excellent agreement with the expected value) and hence proves a transition state was found. From the animation of this vibrational mode it can be seen that the vibration of the transition state at the imaginary frequency corresponds to the bond making/breaking process occurring in the Cope rearrangement. It can also be seen that this process occurs both simultaneously and asynchronously meaning as one bond breaks the other forms. Consequently this proves that the [3,3] sigmatropic Cope rearrangement is a concerted process. Other important structural information is shown below in the table and compared to the frozen coordinate method. Output file for TS Berny calculation DOI:10042/to-8017 .

Frozen Coordinate Method

In this method the drawn transition structure from the previous method was optimised in a different way. Using the frozen coordinate method the terminal carbon atom bond distances between fragments was set to and frozen at 2.2Å by using the 'redundant coordinate editor' to freeze these atoms in place. In the first optimisation the rest of the molecule was allowed to freely move. Using the resulting optimised structure a second optimisation was carried out this time relaxing the constraints on the terminal carbon atom bond distances. A second transition state optimisation was carried out (using the same keywords used in the TS Berny calculation) except this time the force constants were not calculated, instead a normal guess Hessian was used which had been modified to include the information about the two coordinates we are differentiating along. Once again a single imaginary vibrational frequency was calculated with a magnitude of -818cm^-1, this is identical to the TS Berny method and the expected value from the instructions. The presence of a single negative frequency proves the structure obtained was a transition state as opposed to an energy minimum. The structural information is reported along with the information from the TS Berny calculation in the table below. DOI:10042/to-8020

Comparison of Optimisation of Chair Transition States with Different Methods

	TS (Berny) method	Frozen Coordinate method
Structure
point group	C2h	C2h
Optimised Energy/a.u.	-231.61932	-231.61932
Bond forming length/Å	2.02	2.02
Bond breaking length/Å	2.02	2.02
Imaginary Vibrational Frequency/cm-1	-818	-818
Vibration

The table above shows the two transition state structures calculated using the different methods were almost identical (taking into account the error associated with the values obtained from Gaussian). The point group, total energy and bond breaking/forming distances were also calculated to be near identical. Similarly the imaginary vibrational frequency corresponding to the bond forming /breaking vibration were calculated to be the same in both methods showing that the same transition state was found. As a result this demonstrates that either method is equally capable of computing the structure of the transition state, although each method does have its drawbacks. The TS Berny method is faster since it only requires one optimisation however a detailed knowledge of the transition state geometry is required or the optimisation will ultimately fail. Therefore this method may be difficult to apply to transition structures of lesser known or studied reactions. On the other hand the frozen coordinate method requires more than one optimisation as well as a good approximation of the terminal bond distances between the allyl fragments. In conclusion both methods calculated the imaginary vibrational frequency corresponding to the bond breaking/forming modes demonstrating that the reaction occurs in a concerted manner with bond forming/breaking proceeding asynchronously as expected.

Optimising the Boat Transition State

To optimise the boat transition state a different method was employed (QST2). In the QST2 method both the reactants and products were specified and the optimisation will attempt to find the transition state. Therefore the anti 2 structure for the 1,5-hexadiene was drawn and then copied into the same 'MolGroup'. The reactants and products were arranged side by side (as shown in the picture below), however the atom labels on the product had to be edited to correctly match with the reactant. Unfortunately the calculation failed when submitted because in the calculation it linearly interpolated between the two structures, consequently it only translated the top allyl fragment and did not take into account the possibility of rotating around the central C-C bonds. This demonstrates how sensitive the QST2 method is to having the correct geometry for the reactants and products in order to accurately calculate the transition structure. As a result the QST2 method is never going to calculate the boat transition structure from the anti 2 structure of 1,5-hexadiene.

Therefore the structure of the anti 2 conformer was modified to more closely resemble the structure of the transition state. To do this the dihedral angle of the four central C atoms (4-14-6-9) was changed to 0^o and the inside C-C-C bond angle (4-14-6 and 9-6-14 for the reactant, 4-1-10 and 9-10-1 for the product) was changed to 100^o. This gave the geometries shown below. The QST2 calculation was re-run now with the new optimised structures, the resulting output file gave the following information.DOI:10042/to-8038

Modified Boat structures

Optimising boat transition state using QST2 method

	QST2
Structure
Point group	C2v
Energy/ a.u.	-231.60280
Bond Forming & Breaking Length/ Å	2.14
Imaginary Vibrational Frequency/ cm-1	-840
Vibration

The total energy of the boat transition state (eclipsed) is higher than the corresponding chair conformation (staggered), this is as expected as the chair transition state was known to be slightly lower in energy. The reason for this is because in the boat conformation the carbon and hydrogens are eclipsed and therefore give the overall transition state a higher torsional strain compared to that of the chair. Consequently this also would imply that the boat transition state has a higher activation energy compared to the chair conformation which can be shown later. Just like in the chair transition state there was a single imaginary frequency calculated (-840cm^-1) this transition state vibration corresponds to the concerted [3,3] sigmatropic Cope rearrangement and demonstrates that the bond breaking/forming process occurs asynchronously.

Intrinsic Reaction Coordinate (IRC) for the Chair Transition state

The intrinsic reaction coordinate was calculated for the chair transition state (using the optimised structure obtained from the TS Berny calculation). A method contained inside Gaussian allows you to follow the minimum energy path from a transition state down to its local minimum on a potential energy surface. This works by creating a series of points by slightly altering the geometry in the direction where the gradient of the energy surface is steepest. This gives information as to which conformers of 1,5-hexadiene the transition structures combine. Initially the IRC calculation was run to the HF/3-21G level of theory with 50 points along the IRC as well as only computing the force constant once at the start. The resulting geometry obtained after 26 points is shown below which had an energy of -231.689 a.u. Unfortunately the calculation had not reached a minimum therefore the resulting geometry obtained was not the minimum energy structure, although it was very similar in structure to the gauche 2 conformer.DOI:10042/to-8033

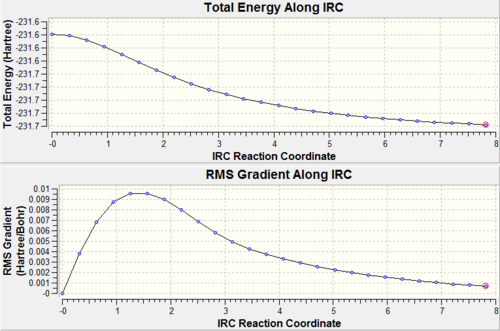
As a result the IRC calculation was re-run in the hope to find the true energy minimum. Therefore the calculation was carried out in the same way with the same level of theory and points along the IRC except this time the force constant was calculated at every step. Using this method gave more accurate results as demonstrated by the graphs from the calculations. It can be seen from the plot that the energy minimum was reached after 47 steps the resulting structure had a total energy of -231.692 a.u. and was remarkedly similar to the gauche 2 conformer.DOI:10042/to-8034

In this calculation the RMS gradient converged to zero therefore the minimum energy geometry was obtained. (since RMS gradient will be zero at the minimum energy).

Activation Energies for the Transition States

Using the chair, boat and anti 2 structures from the HF/3-21G level of theory calculations the activation energies for the reaction via the two transition states can be obtained from the vibrational analysis. However in order to do this each structure must be first optimised to a higher level of theory (B3LYP/6-31G*) and then run the frequency analysis. The thermochemical data was extracted from the resulting output files.

Summery of energies (in Hartree)

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.619322	-231.466705	-231.461340	-234.556984	-234.414928	-234.409008
Boat TS	-231.602802	-231.450932	-231.445303	-234.543093	-234.402335	-234.396001
Reactant (anti2)	-231.692535	-231.539539	-231.532565	-234.611707	-234.469203	-234.461849

DOI:10042/to-8037 : Chair activation energy DOI:10042/to-8041 : Boat activation energy

There is a clear difference in the energy calculated for each method used, although because two different levels of theory were used it is not possible to directly compare them. However the results do show that the more complex basis set gave lower energy values which is expected since they are more accurate. To calculate the activation energies (ΔE) for the transition states, you find the difference between the sum of electronic & zero-point energies for the anti2 conformer and the boat/chair transition states (at 0K). To find the activation energy at 298.15K the same procedure is used except the difference between the Sum of electronic and thermal energies is used in this case.

Activation energies for chair an boat transition states (kcal/mol)

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298 K	at 0 K	at 298 K	at 0 K
ΔE (Chair)	45.70	44.69	34.06	33.16	33.5 ± 0.5
ΔE (Boat)	55.60	54.78	41.96	41.32	44.7 ± 2.0

1 Hartree (a.u.) = 627.509 kcal/mol

As it can be seen from the above table the activation energies calculated from the B3LYP method gave energies in better agreement with the reported values given in The Results Table. The activation energies determined from the HF/3-21G level of theory were on average 10 kcal/mol higher than the reported values. However in both methods used the chair transition state was calculated to have a lower activation energy which is as expected due to minimisation of steric repulsions in the chair conformation compared to the boat. As a result it would be expected that the preferred conformation for transition state would be the chair structure in the [3,3] sigmatropic Cope rearrangement where the anti2 conformer is the starting material and the gauche 3 structure was the product .

Diels Alder Cycloaddition

The Diels-Alder reaction is [4π + 2π] pericyclic reaction involving a conjugated diene with an alkene (dienophile). During the reaction concerted formation of two or more σ-bonds occurs between the ends of two or more π conjugated systems. During this section two reactions are going to be investigated.

During the reaction the HOMO/LUMO of one of the reactants interacts with the HOMO/LUMO of the other reactant to form a pair of bonding and antibonding MO's. The reaction proceeds via a single transition state which is partially stabilised due to slight aromatic character involving 6π electrons.

The simplest Diels-Alder reaction is the reaction between cis-butadiene and ethylene, this reaction will be investigated initially. Then the regioselective Diels Alder between 1,3-cyclohexadiene and maleic anhydride will be investigated. All the optimisations were carried out with the semi-empirical/AM1 method followed by the DFT/B3LYP/6-31G* level of theory. These structures were then used to calculate the properties associated with the transition state with an aim to understand how the reaction proceeds.

Cis-Butadiene with Ethylene

Diels-Alder reaction of cis-butadiene and ethylene

Molecular Orbital Analysis

Cis-butadiene and ethylene were optimised using the semi-empirical/AM1 method. The frontier molecular orbitals (HOMO/LUMO's) were also calculated by adding the additional keywords "Opt=NoEigen". The total energy of the cis-butadiene was 0.04880142 a.u. and the total energy of the ethylene molecule was 0.02619723.

Reactant	Molecular Orbital		Symmetry
cis-Butadiene	LUMO		Symmetric
	HOMO		Anti-symmetric
Ethylene	LUMO		Anti-symmetric
	HOMO		Symmetric

https://wiki.ch.ic.ac.uk/wiki/images/9/96/CISBUTADIENEFINAL.LOG Cis-butadiene

https://wiki.ch.ic.ac.uk/wiki/images/e/ef/WRONG.LOG - Ethylene

As it can be clearly seen from the table above the symmetries of the HOMO and LUMO orbitals (with respect to the reflection plane) for ethylene are opposite compared to cis-butadiene. Therefore due to the preservation of orbital symmetry ( HOMO and LUMO must have same symmetry in order to overlap) the only reaction that can occur is between the HOMO of cis-butadiene and the LUMO of ethylene or the LUMO of cis-butadiene and the HOMO of ethylene. The result of these interactions would yield two new σ bonds in what is described as an allowed Diels-Alder reaction. Therefore from this simple calculation it demonstrates how important orbital symmetry is in determining whether a reaction will proceed and what the stereochemical outcome will be.

Transition State

In order to accurately compute the transition state for the reaction the frozen coordinate method was used. Therefore the calculation was as described before except this time the approximations and basis sets used were modified. Initially the ethylene fragment was placed ~2Å away from the cis-butadiene molecule then the imaginary C-C bond distances between the fragments was frozen to 2.1Å. The resulting geometry was optimised first using the semi-empirical/AM1 method. From this optimised geometry a second optimisation was carried out but this time the C-C bonds were "unfrozen" and the structure was optimised to a TS (Berny) again using the semi-empirical/AM1 method. Finally the calculation was re-run but this time the level of theory was changed to a more complex system again optimising to a transition state but using the DFT/B3LYP/6-31G(d) level of theory. It was important to remember the additional keywords "opt=NoEigen" when the Opt+freq calculations were run to prevent the optimisation from crashing if more than one imaginary frequency was detected.

DOI:10042/to-8051 : Semi-empirical transition state.

DOI:10042/to-8052 : DFT/B3LYP/6-31G(d) transition state.

Optimisation of transition state

	Semi-empirical/AM1 method	DFT/B3LYP/6-31G(d) method
Structure
Energy/ a.u.	0.11166	-234.54390
Bond forming Length/ Å	2.12	2.27
Imaginary frequency/ cm-1	-957	-525
Vibration

It is not really appropriate to compare the energies of the transition states since different approximations and basis sets are used in each method. However it is interesting to compare the different bond lengths calculated between the reacting fragments. For example the C-C bond forming distances were longer by 0.15Å when the DFT/B3LYP/6-31G(d) method was used, the reason for this can be rationalised simply from the fact the different methods were used. Since the TS calculated from the more accurate DFT/B3LYP/6-31G(d) method was lower in energy this implies that the activation energy to the transition state calculated in the DFT/B3LYP/6-31G(d) method is lower than in the semi-empirical method. In both optimisations a single imaginary vibrational frequency was calculated (although only one was shown) confirming that a TS had been found. Despite the fact that the vibration was calculated to occur at different wavenumbers they both corresponded to the same vibration which describes the synchronous formation of the two C-C bonds between the two reactants. The vibration also shows the reaction occurs in a concerted manner which is typical of the Diels-Alder reaction.

The calculated sp³-sp³ C-C bond was found to be 1.40Å, whereas the sp²-sp² C=C bond was found to be 1.38Å, these values match fairly well to the literature values of 1.54Å and 1.34Å respectively. Also the forming σ C-C bonds are both longer than the literature sp³-sp³ C-C bond (2.12Å and 2.27Å) but shorter than twice the van der waals radius of carbon (1.70Å) indicating the newly formed C-C bond is still in the process of forming. Furthermore the slight differences in the bond lengths compared to literature also suggests the π bonds are donating some electron density to the σ bonds, therefore the double bonds become single bonds and vice versa meaning the transition state shows signs of aromaticity, which is consistent with the Diels-Alder reaction mechanism.

Molecular Orbitals

The frontier molecular orbitals (HOMO/LUMO) involved in the transition state are visulaised in the table below.

HOMO and LUMO of transition state

	HOMO	LUMO
Molecular Orbital
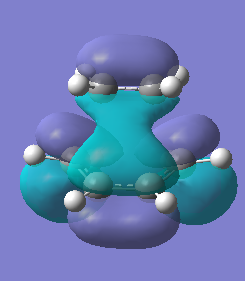
Energy / a.u.	-0.32394	0.02320
Symmetry	Antisymmetric	Symmetric

As it can be seen from the MO's generated above the HOMO of the transiton state is antisymmetric and comprised of the antisymmetric HOMO of the cis-butadiene and the antisymmetric LUMO of the ethylene thereofre the orbital sysmmetry has been preserved on forming the moleuclar orbitals (molecular orbitals formed from the overlap of reactant molecular orbitals must have the same symmetry). Conversely the LUMO is made up of the HOMO of the ethylene and the LUMO of the cis-butadiene again with the orbital symmetry conserved. From the visual analysis of the HOMO it can be seen there is a large amount of elelctron density located between the cis-butadiene and ethylene molecules as expected. Also since there are 6 electrons (4n+2) involved in the transition state according to the pericyclic selection rules (thermal conditions) the reaction should proceed via a Huckel aromatic transition state with the bond forming suprafacially (i.e. the bonds form on the same side of the molecule).

Activation Energy

By optimising both the reactants to the DFT/B2LYP/6-31G(d) level of theory and performing a frequency analysis to the same level. The activation energies could then be calculated by finding the difference between the sum of electronic and thermal energies of the reactants (when the two are combined) and the transition state at 298.15K.

DOI:10042/to-8073 : Ethylene (AM1) DOI:10042/to-8074 : Ethylene (DFT) DOI:10042/to-8075 : cis-butadiene (AM1) DOI:10042/to-8076 : cis-butadiene (DFT)

Summary of energies (Hartree)

	AM1	B3LYP/6-31G
	Sum of Electronic and Thermal Energies (a.u.)	Sum of Electronic and Thermal Energies (a.u.)
	at 298K	at 298K
Ethylene	0.080254	-78.533177
cis-Butadiene	0.138574	-155.896784
Reactant Total	0.218828	-234.429961
Transition State	0.259453	-234.396908

The difference was then found and reported in kcal/mol, 1 Hartree = 627.509 kcal/mol

Activation energies

	AM1	B3LYP/6-31G	Experimental.
	at 298K	at 298K	0K
Activation Energy / a.u.	0.040625	0.033053	-
Activation Energy / kJ/mol	106.70	86.78	115
Activation Energy / kcal/mol	25.50	20.74	-

The values calculated seem to give quite surprising results, since the less accurate method and basis set (AM1) gave more accurate estimates for the activation energy of the reaction. The values obatined from the semi-empirical method were in closer agreement with the literaturevalue obtained at 115 kJ /mol at 0K.

Cycloaddition of Cyclohexa-1,3-diene with Maleic Anhydride

Another example of the Diels-Alder reaction is the cycloadditon of cyclohexa-1,3-diene with maleic anhydride. However this reaction differs from the previous example as theoretically two diastereisomers are formed during the reaction, the endo and exo products. The different products exist due to the two different ways the diene (cyclohexa-1,3-diene) can approach the dienophile (maleic anhydride), depending on the approach two diatereoisomers are formed. However it is known from many experiments that the endo product is the major isomer, although the endo product in this reaction is also the kinetic product and therefore is formed fastest and this is due to a secondary orbital interaction (SOI). As a result it would be expected that the endo transition state will be lower in energy than the exo transition state. By using the methods already described in previous examples this will be proven computationally.

Cycloaddition of Cyclohexa-1,3-diene with Maleic Anhydride

Transistion State Optimisation (Endo/Exo) and Imaginary Frequency Analysis

The reactants were optimised using the exact same procedure as for the cis-butadiene and ethylene molecules, cyclohexa-1,3-diene and maleic anhydride were first optimised separately using the semi-empirical/AM1 method. The two fragments were then copied into the same window in Gaussview and rearranged to what the transition states might look like and re optimised using the frozen coordinate method. Initially the "new bonds" distance between the molecules was frozen to 2.2Å and the re-optimisation was performed using the same level of theory. Finally the bonds were "unfrozen" just like before and the resulting transition structures were optimised (plus the frequency calculation,Opt+freq) optimising this time to a TS (BERNY) first using the semi-empirical method and then again using the more complex DFT/B3LYP/6-31G(d) method. The resulting geometries, imaginary vibrational frequencies and average bond forming lengths are all reported below for the endo and exo products.

Comparison of optimisation of transition states

	Exo TS		Endo TS
	AM1	B3LYP/6-31G*	AM1	B3LYP/6-31G*
Structure
Energy/ a.u.	-0.05042	-612.67931	-0.05150	-612.68340
C-C bond forming length (Å)	2.17	2.29	2.16	2.27
Imaginary Frequency/ cm-1	-813	-449	-807	-447
Vibration

Exo TS AM1:DOI:10042/to-8062 Exo TS DFT:DOI:10042/to-8063

Endo TS AM1:DOI:10042/to-8060 Endo TS DFT:DOI:10042/to-8061

It was observed in all the calculations that a single imaginary vibrational frequency was calculated leading to the conclusion that a transition state had been found successfully. Also just like before the vibration corresponds to the synchronous formation of the two new C-C σ bonds which is consistent with the concerted reaction mechanism expected from a Diels-Alder reaction. Furthermore it was found that the endo transition state energy was lower then the corresponding exo transition state, this implies that the endo TS will have a lower activation energy barrier and is hence more thermodynamically stable. Since this Diels-Alder reaction is under kinetic control the transition state with the lowest energy (smallest activation energy) will lead to the dominant product i.e. the endo product. This was confirmed by Alder et al. The reason for the endo products increased stability originates from a secondary orbital overlap between the (O=C)-O-(C=O) fragment and the newly formed C=C double bond, it will be shown later but it is important to note that this interaction can only exist in the endo product rather than the exo . The bond distances in both transiton states were very similar, this is exemplified by the very similar bond forming distances observed in both methods used. On initial inspection of the structures it might be expected that the endo transition state would be the least favoured TS becasue it suffers from a steric repulsion or better described 1,3-diaxial compression between the sp³ hydrogens on the cyclohexadiene with the hydrogens at the back of the maleic anhydride. However this is not the case as previously mentioned the endo TS was lower in energy because of the secondary orbital interaction (SOI) present in the endo product. This might also explain why the bond distances between the two reactants in the transition state were smaller for the endo product as it benefits from this stabilisation. Finally another reason the endo product is lower in energy is due to the minimisation of steric strain, as in the transition state the C-C-C bond angle between the C=C bond and sp² carbon atom on the maleic anhydride (i.e. where the new bond between reactants forms) is 99^o which is much closer to an idealised sp³ carbon (109^o) compared to the exo product (95^o).

Molecular Orbital Analysis

The frontier molecular orbitals of the endo and exo transition states (HOMO/LUMO) were visualised in an attempt to try and understand the secondary orbital interaction. (Orbitals taken from the DFT/B3LYP?6-31G(d) level of theory).

Molecular Orbital	endo			exo
	Diagram	Energy (a.u.)	Symmetry	Diagram	Energy (a.u.)	Symmetry
LUMO		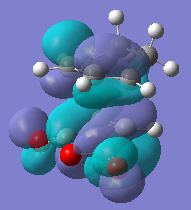-0.067	Anti-Symmetric		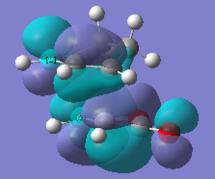-0.078	Anti-Symmetric
HOMO		-0.242	Anti-symmetric		-0.242	Anti-symmetric

As it can be seen from the table above the HOMO and LUMO's of the transition states are both antisymmetric. In both the endo and exo transition states the HOMO describes the newly forming σ bond between the two reactants. The bond is formed from the overlap of the HOMO of the cyclohexa-1,3-diene and the LUMO of the maleic anhydride. During the Diels-Alder reaction the electron density is donated in to the LUMO of the C=C bond on the maleic anhydride moiety and since this is the π* anti bonding orbital this weakens the C=C bond and forms a C-C single bond as seen in the products.

As previously mentioned the endo transition state is stabilised by a secondary orbital overlap (SOI), the primary orbital overlap is shown by the HOMO's in the above table and corresponds to a σ bond being formed whereas the secondary orbital interaction does not form a bond but is more of a stabilising interaction. The interaction occurs between the carbon atoms adjacent to the carbon atoms forming the new bond (the other two sp² carbons from the original cyclohexadiene) and the carbon atom of the π* C=O orbital on the maleic anhydride molecule. The interaction occurs between in phase orbitals of the carbon atoms in the π conjugated system and the carbon atoms of the π* orbitals of the C=O bond. This interaction stabilises the endo transition state and as a result lowers the energy and consequently the activation energy, and since the reaction is under kinetic control the fastest formed TS will lead to the major product therefore the endo isomer dominates. The secondary orbital interaction has a distance of 2.99Å compared to the exo product which does not benefit from the same secondary orbital overlap since the maleic anhydride points in the opposite direction so the SOI distance is much larger at 3.88Å (and hence there is no effective overlap).

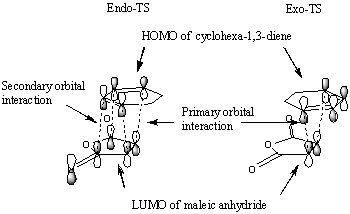
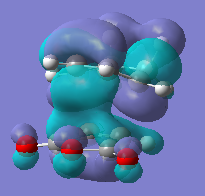
It would be expected that from consideration of the linear combination of atomic oritals (LCAO) the secondary orbital interaction would be observable in the HOMO of the endo transition state. However there is very little electron density observable between the newly formed C=C double bond and the carbon atoms of the (O=C)-O-(C=O) fragment instead a nodal plane is seen in this region. The reason for this may be due to the inaccuracies of the level of theory used to generate the molecular orbitals. For example when different approximations and basis sets are used the ordering of the molecular orbitals can change, for this reason other molecular orbitals around the HOMO/LUMO region were visualised in the hope of finding a molecular orbital which effectively demonstartes the secondary orbital interaction. The image on the left is the LUMO+2 molecular orbital of the endo transition structure and shows electron density between the forming C=C bond and the carbon atoms of the (O=C)-O-(C=O) fragment, (albeit the LUMO+2 by defintion is unoccupied) but due to the inaccuracies in the method used to generate the MO's could still represent the SOI.

Activation Energy

By optimising both the reactants to the DFT/B2LYP/6-31G(d) level of theory and performing a frequency analysis to the same level. The activation energies could then be calculated by finding the difference between the sum of electronic and thermal energies of the reactants (when the two are combined) and the transition state at 298.15K.

DOI:10042/to-8077 : Maleic anhydride (AM1) DOI:10042/to-8078 : Maleic anhydride (DFT) DOI:10042/to-8079 : cyclohexa-1,3-diene (AM1) DOI:10042/to-8080 : cyclohexa-1,3-diene (DFT)

Summary of energies (in Hartree)

	Semi-empirical/AM1		B3LYP/6-31G
	Sum of Electronic and Thermal Energies (a.u.)		Sum of Electronic and Thermal Energies (a.u.)
	at 298K		at 298K
Cyclohexa-1,3-diene	0.157031		-233.288616
Maleic anhydride	-0.058191		-379.228475
Reactant Total	0.09884		-612.517091
Transition State	endo (AM1)	exo (AM1)	endo (DFT))	exo (DFT)
	0.143686	0.144892	-612.491782	-612.487660

The difference was then found and reported.

Activation energies ((Hartree)

	Semi-empirical/AM1	B3LYP/6-31G
	at 298K	at 298K
endo Activation Energy / a.u.	0.044846	0.025309
exo Activation Energy / a.u.	0.046052	0.029431

As it can be seen in both methods used the activation energy for the endo transition state was always lower than the exo TS. Consequently whenever the reaction is under kinetic control the TS with the lowest energy will lead to the major product therefore the endo product will be the major isomer of the reaction. It is important to note that there is an error in Gaussian associated with the calculation of the energies of around 5kJ/mol therfore the difference in the activation energies may not in reality be as significant.

Conclusion

This exercise has demonstrated how the transition states for a series of reactions can be modelled as well as computing the imaginary vibrations (corresponding to the bond fomring processes), molecular orbitals and thermochemical data associated with them. By predicting the transition state geometries, MO's, activation energies etc the most likely outcome of a reaction can be effectively rationalised. As with all calculations using Gaussian there is often a trade off between accuracy and time, the calculations performed here have demonstrated that often a more complex basis set such as B3LYP/6-31G(d) can give more accurate results (as well as less accurate as seen in the Diels-Alder reaction of ethylene and cis-butadiene). If more time were allowed some of the reagents would have been optimised to a higher level of theory although this would require more computing power and thereofore increase costs. Consequently the B3LYP/6-31G(d) has proven to be an excellent compromise between accuracy and time. One of the major drawbacks of Gaussian calculations was highlighted in the Diels-ALder reaction of maleic anhydride with cyclohexa-1,3-diene, in that it cannot tell whether the reaction will procced via thermodynamic or kinetic control since at this moment in time it can only be determined experimetally.