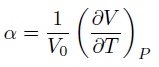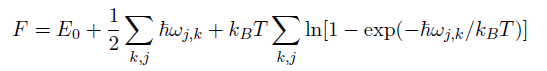Rep:Mod:Jotaro

Thermal Expansion of MgO (by Wern Ng)

Introduction

The system to be studied is a regular MgO crystal lattice, which has a cubic conventional cell. The aim is to calculate the thermal expansion coefficient denoted by:

Two methods will be used to calculate the coefficient:

• Quasi-harmonic approximation

The MgO crystal has many phonon modes, each corresponding to a certain frequency labelled by a k-value. The energy of a mode can be calculated from its frequency, and so the sum over all the phonon energies would be used to calculate the free energy of the crystal. Since the Helmholtz Free Energy is a function of temperature and volume (i.e. we have A(T, V)), the crystal would be simulated at a certain temperature, and the phonon energies summed. A diatomic molecule with an exactly harmonic potential (a pure harmonic approximation) would have the equilibrium bond distance remain the same no matter the energy given, which would result in the lattice parameter never changing with temperature. Therefore, after summing the energies of the phonon modes, the quasi-harmonic approximation varies the lattice parameters (which relate to the crystal volume) until a minimum in free energy for the crystal is reached (thus allowing a change in equilibrium bond distances which wouldn't be observed for a pure harmonic approximation)

The quasi-harmonic approximation assumes that all the phonon modes in the crystal can be represented by a simple harmonic oscillator, and that their energies can be determined using SHO equations.

• Molecular Dynamics

The molecules are simulated to vibrate purely through force interactions (such as through ionic Coulomb potentials and changing temperatures), and an average is taken over all the atomic motions to reach a free energy. It does not rely on a SHO approximation, and though it will be more accurate (since atomic potentials aren't fully SHO), the calculations take more time.

The computing tool used was DLVisualize within a Linux distribution.

Initial Lattice Energy and Volume

The initial internal energy and volume of the MgO crystal was calculated. The report section is given below (with the primitive cell lattice parameters listed)

  Cartesian lattice vectors (Angstroms) :

        0.000000    2.105970    2.105970
        2.105970    0.000000    2.105970
        2.105970    2.105970    0.000000

  Cell parameters (Angstroms/Degrees):

  a =   2.9783    alpha =  60.0000
  b =   2.9783    beta  =  60.0000
  c =   2.9783    gamma =  60.0000

  Initial cell volume =     18.680416 Angs**3

Total lattice energy = - 41.0753 eV

Initial cell volume = 18.6804 Angstrom³

  This calculation was carried out at 0 K. The lattice energy is the binding energy of a single primitive cell, and the initial cell volume is the V₀ value in the thermal expansion equation, to be used later.

Phonon Dispersion

Every type of vibration of an infinite crystal lattice can be described by a k-value (in 3D, k is a vector of 3 values), which will give the frequency ω of the vibration (hence 'describing' it). This is analogous to how k-values can describe electronic energy states (E(k)).

The x-axis corresponds to the symmetry points in k-space.

There are six frequency readings (branches) per k-point because there are two atoms per basis (with 1 AO each), in three dimensions (3 x 2 = 6).

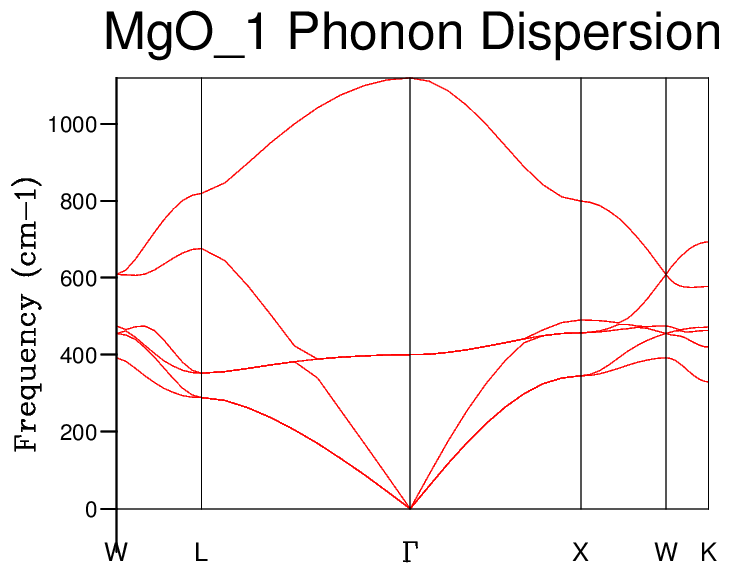
Phonon DOS

The DOS measures how many vibrational states are within a certain frequency interval. In relation to the dispersion curve, the DOS is usually inversely proportional to the slope of the dispersion curve (which plots frequency against k). A larger DOS for a certain frequency interval indicates that the dispersion curve slope for that frequency interval is quite flat (and that there are more states within that interval).

The DOS was calculated initially using a single k-point for the average (1 x 1 x 1 grid), which is definitely not very representative of the entire lattice.

Cross-checking the peak frequencies of the DOS curve and the frequencies listed in the dispersion curve show that the single k-point chosen for the 1 x 1 x 1 grid was the L-symmetry point (0.5, 0.5, 0.5):

DOS log

 Phonon Calculation : 

  Number of k points for this configuration =    1

--------------------------------------------------------------------------------
    K point   1 =   0.500000  0.500000  0.500000  Weight =    1.000
--------------------------------------------------------------------------------
  
    Frequencies (cm-1) :
  
    288.49  288.49  351.76  351.76  676.23  818.82

Phonon Dispersion log

--------------------------------------------------------------------------------
  K point  10 =   0.500000  0.500000  0.500000  Weight =    0.020
--------------------------------------------------------------------------------
  
   Frequencies (cm-1) : 
  
    288.49  288.49  351.76  351.76  676.23  818.82

It is the 10th point sampled in the phonon dispersion

The correspondence can be seen visually when comparing the DOS curve with the dispersion curve. They are shown side-by-side below with blue circles to highlight the correspondent frequencies.

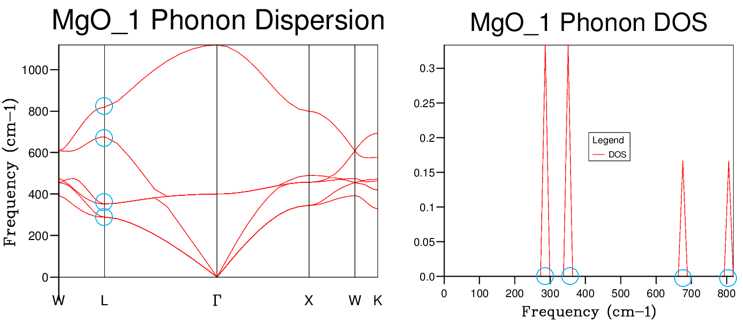
Grid size and DOS accuracy

As a larger number of k-points are sampled (using a larger grid), the resolution of the DOS curve increases and reveals more features. For a 100% accurate DOS, an infinite amount of k-points must be sampled, which will require sampling over a truly infinite lattice to characterize every single kind of vibration labelled by a k-value. This is practically impossible, so to balance the computation time with the accuracy, the DOS curve was plotted using increasing shrinking factor grid sizes.

After achieving a grid size of 10 x 10 x 10 the DOS begins to take on a more spectral (rather than discrete) form, and increasing grid sizes smooth out parts of the curve and begin revealing fine structure. A grid of 10 x 10 x 10 or smaller has the calculations finish instantly. For grids above 20 x 20 x 20 k-points, the calculations take about one minute.

As can be seen, the resolution increases up to about the 40 x 40 x 40 grid, after which increasing grid sizes make little difference. A 50³ grid gave a good resolution within a reasonable time scale (about 3 minutes), while a 60³ grid gave a similar resolution after a calculation time of 7 minutes. Calculating using a 70³ takes more than 20 minutes, so the 50³ grid was chosen as the minimum grid size for an optimal approximation of the DOS.

DOS grid sizes for alternate materials (speculation)

The optimal grid size chosen was 50³ for MgO.

When comparing against similar oxides, such as CaO, only the cation would have changed. The conventional cell used (cubic) and the ionic potentials would be identical, so the only difference would be the lattice distances due to differing ionic radii (affecting lattice parameters). This may affect orbital overlap distances and hence change the features of the DOS curve, but the accuracy of the calculation shouldn't be affected. The grid size used for MgO should still be optimal for CaO since nothing else has changed except possibly the lattice parameter, and the difference wouldn't be very significant.

For zeolites, the lattice parameter of a zeolite cell such as faujasite is about 24 angstroms. This is about eight times larger than the parameters calculated for MgO (about 3 angstroms in the initial energy calculation). Reciprocal space is related to real space (in one dimension) by:

a' = 2π / a

So the larger lattice of a zeolite will have a much smaller reciprocal space lattice, meaning that zeolites require less k-points than MgO to achieve a similar resolution of the DOS (i.e. zeolites can achieve a similar resolution with a smaller grid).

Finally, for a pure metal such as lithium, the atoms use metallic bonds featuring cations surrounded by a sea of delocalized electrons. For phonons, the electrons effectively shield all the cations from repelling each other away, so the vibrations are severely dampened. This leads to a flatter phonon dispersion curve, which corresponds to a relatively featureless DOS curve. Therefore a much smaller grid size can be chosen to express the DOS of lithium, rather than 50³.

Using free energy to confirm the suitability of the k-space grid

The previous DOS curves were calculated at 0 K. In this section, the DOS curves were calculated for the same k-space grids, but at 300 K. The resolution of the curves increases with grid size at 300 K similarly to the DOS curves at 0 K, so the graphs are not displayed.

The free energies of each crystal against k-space grid size is shown below:

Grid Size (n x n x n)	Free Energy (eV)	ΔE (eV)
1	-40.930301	N/A
2	-40.926609	0.003692
4	-40.926450	0.000159
10	-40.926480	-0.000030
20	-40.926483	-0.000003
30	-40.926483	0.000000
40	-40.926483	0.000000
50	-40.926483	0.000000
60	-40.926483	0.000000

(more significant figures are included for these values in order to detect the change of ΔE)

The free energy calculation relies on the equation below:

It utilizes averages of all the phonon frequencies of the crystal, so the larger the k-value grid the more accurate the average.

The ΔE value is the difference between the current grid size free energy and the preceding grid size free energy (e.g. ΔE for grid size 50 is E(grid size 50) - E(grid size 40)). As the DOS becomes more accurate by including more k-values, the free energy also converges to its most accurate value (as can be attained by simulation). This can be represented by ΔE approaching zero, so it can be seen that a grid size of 30 x 30 x 30 is enough to reach convergence for the free energy. This further assures that a grid size of 50, which was chosen after visually assessing the DOS curve resolution, is adequate enough for further calculations.

The ΔE values further indicate which grid sizes are appropriate for calculations up to a certain accuracy. A grid size of 4 x 4 x 4 is capable of an accuracy up to 1 meV, and a grid size of 10 x 10 x 10 is capable of an accuracy up to 0.5 meV and 0.1 meV.

Quasi-harmonic Approximation

Using the quasi-harmonic approximation, a k-space grid of 50 x 50 x 50 was used to calculate the lattice parameters of the MgO crystal that gave the minimum free energy at a specific temperature. The lattice parameters were then used to calculate the cell volume, which was plotted against temperature to find the thermal expansion coefficient.

When the lattice parameter and cell volume were plotted against temperature, they showed non-linear behavior for lower temperatures (from 0 K to 200 K), where curve flattens out. Higher temperatures showed a linear relation between the free energy/cell volume and the temperature. Therefore the linear fit was plotted excluding the cell volume attained at 200 K and below (the non-linear behavior will be further discussed in the MD section). The free energy was also plotted against temperature, and it decreases with temperature because of the relation A = U - TS. So with increasing temperature and entropy, the free energy will decrease since it is the negative part of the equation.

To calculate the thermal expansion coefficient, the gradient of a linear fit through the volume vs temperature graph was taken to be 0.0005 angstrom³/Kelvin (the fit has a good reliability with R²=0.997). If this is multiplied with the reciprocal of the initial cell volume (previously calculated as 18.6804 angstrom³), we have:

α = 1/(18.6804) x 0.0005 = 2.677 x 10^-5 K^-1

This is slightly larger than the experimental literature value which is 1.29 x 10^-5 K^-1 measured at 500 K (the midpoint temperature of our simulation), but this is quite a good result considering that it was calculated almost solely from assuming SHM potentials for all phonon vibrations. There could be many more interactions within a real MgO crystal which would not have been considered under a quasi-harmonic approximation. A better representation of atomic potentials is the Lennard-Jones potential, which is not considered by the quasi-harmonic approximation, which can lead to the discrepancies with the literature.

The main approximation of this method was that every phonon mode can be represented as an SHO, but such a potential will never allow bonds to break no matter the temperature. Such an approximation is valid at low temperatures, but at high temperatures a more accurate ionic potential must be considered (usually a Lennard-Jones potential). In fact, when approaching the melting point of MgO (about 3000 K), since the quasi harmonic approximation bases itself upon perfect harmonic oscillations the bonds will never weaken and break to allow a transition into the liquid state. The MgO crystal will simply be simulated to expand forever at increasing temperatures.

Thermal expansion physically comes from additional heat in a material being converted to more energetic vibrations of atoms in the material, causing them to occupy more space and increase the overall material volume.

For speculation on the change of bond distance for a diatomic molecule with an exactly harmonic potential, refer to the Introduction section

Molecular Dynamics Approximation

An MgO cell consisting of 32 MgO formula units was used for this calculation. The bond distance between Mg and O in this cell was 2.106 angstroms, which corresponds well to the lattice parameter calculated for the initial optimization exercise. Once again, the amount of formula units used is a compromise between having more formula units (allowing more k-values to be sampled) in the simulation to get a more accurate result and being limited in computation time. The following is a plot of the changing cell volume per formula unit versus temperature, compared with the quasi-harmonic simulation.

To calculate the thermal expansion coefficient, the gradient of a linear fit through the points was taken and recorded as 0.0006, with a good reliability (R²=0.999). This gradient value is very similar to that attained from the quasi-harmonic approximation. This is propagated through the same equation used previously in the QH case:

α_MD = 1/(18.6804) x 0.0006 = 3.2 x 10^-5 K^-1

The value computed is slightly higher than that of the QH method, and higher than the literature value. The reasoning is also similar to the QH approximation in that there could be other processes occurring beyond simple force interactions which MD is based on. Additionally, the cell used for MD calculations (32 formula units) is smaller than the lattice used for the QH calculations, since QH involves using a 50 x 50 x 50 grid of k-points, and some of those k-values will involve phonons that utilize a lattice much larger than 32 formula units. Hence it could be speculated that a larger cell size for the MD simulation could cause the calculated gradient to lower and converge to a value that would compute closer to the thermal expansion coefficient of the literature.

Comparing MD and QH (further speculation)

Previously there was non-linear behavior observed in the free energy and volume vs temperature curves for the QH method. This is due to the QH method taking into account the residual zero-point vibrational energy of the phonons, whereby if the atoms are in the vibrational ground state (which is the case at 0 K) they will still contain some vibrational kinetic energy despite the temperature being 0 K (quantum mechanically, the ground state energy can't be zero or else the ground state wavefunction vanishes). Therefore the vibrational energy of the lattice doesn't go straight to zero and this causes the non-linear behavior seen in the free energy and volume curves.

Therefore, QH would be more suitable to simulate behavior of the MgO lattice at lower temperatures than MD since it takes into account the zero-point energy. As can be seen, MD decreases linearly even down to 0 K since it only simulates forces between molecules, and the kinetic motions of the molecules would be predicted to stop completely at 0 K. MD does not take the quantum mechanical effects of vibrations into account (i.e. the zero point energy).

Conversely, MD is more suitable than QH for simulating behavior at higher temperatures. As previously remarked, QH would have the lattice expand indefinitely at higher temperatures, while MD takes into account inter-ionic forces and would allow bond breaking. So at higher temperatures the MD simulation may feature the lattice breaking apart near the melting point. Hence MD would be more appropriate for simulating temperatures near the melting point of MgO.

Finally, the previously computed free energies from changing the grid size of the DOS converged after using a grid size of 30 x 30 x 30. Therefore, a real space cell size corresponding to this k-space grid size would be adequate to reliably perform MD.

Conclusion

The lattice parameters and free energies of the MgO crystal against varying temperatures were calculated using the quasi-harmonic and molecular dynamics simulations.

Initially, free energy calculations were used to determine the appropriate k-point sample size (k-space grid) to use for the QH simulation which balanced accuracy with computation time. A grid size of 50 x 50 x 50 was chosen.

It was found that both simulations calculated the thermal expansion coefficient slightly higher than the literature value, but were in good agreement in terms of the magnitude. The discrepancy is due to assumptions made for the simulations (e.g. QH assumes that the phonons are represented by SHO) as well as the compromise between accuracy and computational efficiency (e.g. MD has a cell consisting of 32 formula units, and larger cells give more accurate results but take longer to compute).

QH uses assumes all phonon vibrations can be represented as simple harmonic motion, and calculates an optimal lattice parameter by varying it to minimize the free energy (calculated using the phonon energies). MD simulates the movement of all the ions based on force interactions. The results obtained through these two simulations slightly differed from each other at higher temperatures, due to MD utilizing a smaller sample space of the lattice than QH, which would sample a larger lattice based on the 50 x 50 x 50 k-space grid used for its simulation. They differed more drastically at the lowest temperatures (approaching 0 K), since QH took into account the quantum effect of zero-point energy allowing for residual vibrational energy in the lattice, while MD would have calculated the kinetic energy within the lattice to be zero at 0 K.