Rep:Mod:Johnny Bravo

=Module2:Inorganic. Woah! = NOTE Energies, when converted from atomic units (Hartree) to kJ/mol have used the value of 1 Hartree = 627.5094kJ/mol. ==Borane.Yah, pretty boring.
==
===Geometry optimisation. Oh Mama!
=
After the BH3 molecule is created, it is optimised using the B3LYP method and the low-level basis set 3-21G. This basis set is suitable as the Borane is a simple molecule with high symmetry. The calculation summary is listed below.
| Optimised Bond Distance | 1.19Å |
|---|---|
| Optimised Bond Angle | 120° |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| Total Energy | -26.462a.u. |
| RMS Gradient Norm | 0.00021a.u. |
| Dipole Moment | 0 |
| Point group | D3h |
The geometrical combination of the atoms in space give a potential surface in which Gaussian iteratively tries to find a point of zero gradient change. This can either be a minima or maxima but Gaussian will try and find a minimum.
===Acquiring the BH3 Vibrations. Wanna dance?.. No?
=
| Calculation Type | FREQ |
|---|---|
| Calculation Method | RB3LYP |
| Basis Set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| Total Energy | -26.462a.u. |
| RMS Gradient Norm | 0.00021a.u. |
| Dipole Moment | 0 |
| Point group | C3h |
The table below shows the six vibrational modes as calculated using Gaussian using the B3LYP method and the 3-21G basis set.
| Vibration Number | Description | Frequency (cm-1) | Intensity | Symmetry (D3h Point group) |
|---|---|---|---|---|
| All within σh plane. All three H atoms vibrate in phase perpendicular to the σh plane. | 1144.15 | 98.9 | A''2 | |
| Scissoring of 2 H atoms along σh plane centred on C21 axis. | 1203.64 | 12.3 | E' | |
| Rocking by two H atoms and an oscillation of last H atom about its C2 axis. | 1203.64 | 12.3 | E' | |
| Totally symmetric stretching by all three H atoms. This results in no net dipole change and so is not observed by I.R. spectroscopy. | 2598.42 | 0.0 | A'1 | |
| Assymetric stretching between two H atoms along σh plane whereas third H atom is stationary. | 2737.44 | 103.7 | E' | |
| Symmetric stretching between two H atoms along σh plane and third atom stretches with double the amplitude along the C21 axis. | 2737.44 | 103.7 | E' |
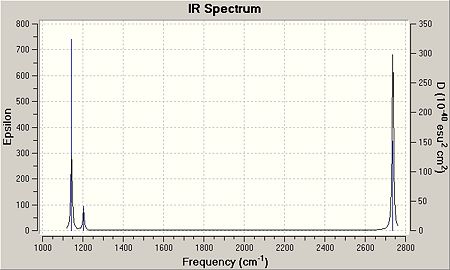
As can be seen above, there are six modes of vibration with D3h symmetry. The vibration at 2598cm-1 is totally symmetric; resulting in the absence of an I.R. peak due to no net dipole change of the molecule. This can be seen in the image below. As there are two pairs of degenerate stretches, namely at 1203cm-1 and 2737cm-1, these peaks merge into one peak of double intensity.
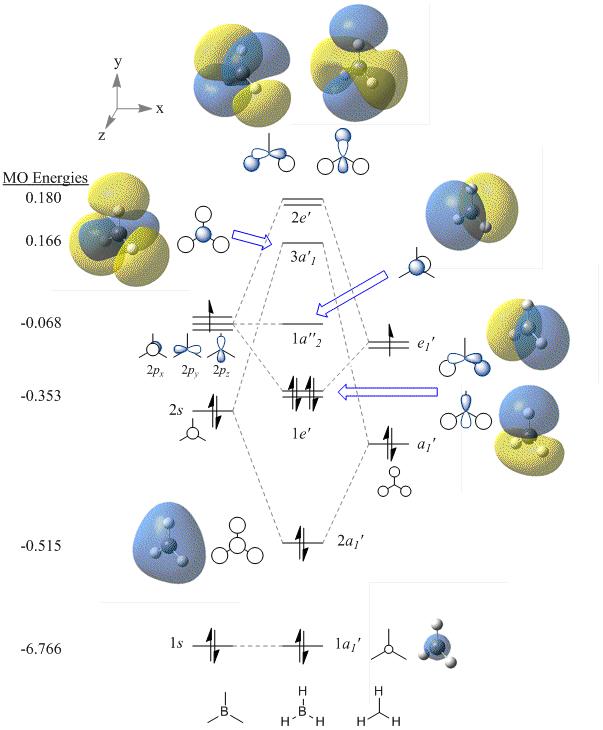
The Molecular Orbital diagram of BH3
The MO energies for BH as calculated using B3LYP/6-31G are listed on the left hand side of the MO diagram below. A 3D rendering is shown next to the qualitative representation of the orbitals.
==Trichloroborane. Want VIP tickets to the gun show? ==
Optimisation
The boron trichloride molecule was optimised using two basis sets; the one used to optimise borane (3-21G) and then the LANL2MB. The difference being that the latter uses a mixture of two basis sets, one applied to light elements (boron in this case) and one applied to heavier elements (Cl).
| Basis set | Set: 3-21G | Set: LANL2MB |
|---|---|---|
| Optimised Bond Distance | 1.78Å | 1.87Å |
| Optimised Bond Angle | 120° | 120° |
| Calculation Type | FOPT | FOPT |
| Calculation Method | RB3LYP | RB3LYP |
| Basis Set | 3-21G | LANL2MB |
| Charge | 0 | 0 |
| Spin | Singlet | Singlet |
| Total Energy | -1398.80a.u. | -69.44a.u. |
| RMS Gradient Norm | 0.000024a.u. | 0.0000093a.u. |
| Dipole Moment | 0 Debye | 0 Debye |
| Point group | D3h | D3h |
Surprisingly, using the 3-21G basis set gives a more accurate bond length within 0.04Å as given by the literature[1] value of 1.742Å. The length calculated using the LANL2MB basis set is 0.13Å off. The Cl-B-Cl angle calculated by both methods are 120° which agrees very well with the literature value of 120°±3°.
It is counter-intuitive that the 3-21G basis set will give a more accurate result than the LANL2MB mix. This can be attributed to the difficulty in setting good pseudopotentials for chlorine.
Why must you use the same method and basis set for both calculations?
The same basis set and method is used to calculate the properties of isomers. This is so that the relative energies of the isomers can be calculated which can give us values resembling empirical observations. The same principle applies when calculating the molecular vibrations after geometrical optimisation. Both calculations need to be performed using the same method and basis set to keep a uniformity in the calculations. The energies calculated from one set will differ wildly from another.
Why do you have to carry out a frequency analysis?
A frequency analysis calculates the second derivative of the energy against geometry curve. This way, we can make sure that the optimisation, which is the first derivative of said curve, has calculated a minima (second derivative is positive) and not a maxima (second derivative is negative).
In some structures gaussview does not draw in the bonds where we expect, does this mean there is no bond? Why?
Gaussview connects two atoms together when they are a specific distance apart determined by the program. If the internuclear distance is greater than the threshold, Gaussview will not recognise it as a bond. This, however does NOT mean that one doesn't exist.
What is a bond?
A bond exists when atoms interact to form an energy minima; that is the total energy is lower when they are at close proximity than if they were alone in free space. In observable terms, a bond can be a concentration of electron density between two atomic nuclei or a direct electrostatic interaction between atoms who have a charge imbalance
What symmetry do you expect for the ground state structure, and what symmetry does gaussview use? Comment briefly on this.
The symmetry used by Gaussview is D3h which is what one would expect of a trigonal planar molecule.
How long did your calculations take?
The LANL2MB calculation took 10.0s to optimise the molecule of BCl3 and 12.0s to calculate the vibrational modes. They were done interactively on the laptop because they are quick enough. More complex calculations will be submitted to SCAN (SuperComputer At Night) as performing them on the laptop would take a considerably longer time.
| Vibration Number | Description | Frequency (cm-1) | Intensity | Symmetry (D3h Point group) |
|---|---|---|---|---|
| Rocking by two Cl atoms and an oscillation of last Cl atom about its C2 axis at double amplitude. | 214.12 | 4 | E' | |
| Scissoring of 2 Cl atoms along σh plane centred on C21 axis. | 214.12 | 4 | E' | |
| All three Cl atoms vibrate in phase perpendicular to the σh plane. | 377.16 | 44 | A''2 | |
| Totally symmetric stretching by all three Cl atoms. This results in no net dipole change and so is not observed by I.R. spectroscopy. | 417.07 | 0 | A'1 | |
| Assymetric stretching between two Cl atoms along σh plane whereas third Cl atom is stationary. | 938.87 | 259 | E' | |
| Symmetric stretching between two Cl atoms along σh plane and third atom stretches with double the amplitude along the C21 axis. | 938.88 | 259 | E' |
Mo(CO)4Cl2 cis/trans geometries
Both the version of Mo(CO)4Cl2 and the version were constructed and optimised using an extra basis set (B3LYP/LANL2DZ+Extra).
The frequencies for both isomers were calculated to make sure the optimisation converged.
| Bond distances | B3LYP/LANL2MB | B3LYP/LANL2DZ+Extra | ||
|---|---|---|---|---|
| TRANS | CIS | TRANS | CIS | |
| P-Cl | 2.40 | 2.41 | 2.11 | 2.12 |
| Mo-P | 2.48 | 2.52 | 2.42 | 2.48 |
| CO | 1.19 | 1.19 | 1.17 | 1.18 |
| Mo-C | 2.11 | 2.11 | 2.06 | 2.05 |
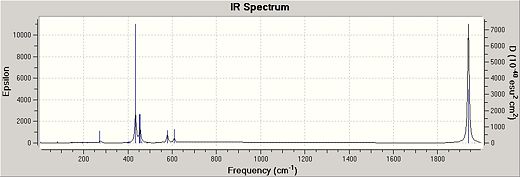
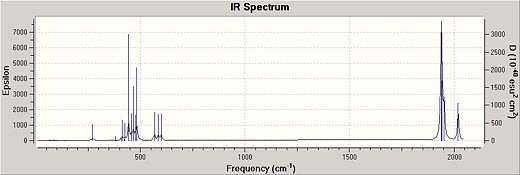
The IR spectrum is shown for both CIS and Trans geometries below:
| TRANS http://hdl.handle.net/10042/to-4490 | CIS http://hdl.handle.net/10042/to-4489 |
|---|---|
|
|
As can be seen, the trans form has fewer stretches. This is expected as the trans geormetry is more symmetrical and therefore contains more degenerate vibrational energy levels.
There is an extra carbonyl peak seen at 2000cm-1 in the cis geometry not noticed in the trans spectrum[2].
| MoCo Vibrations | |||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
Project: Using Borazane as a Hydrogen storage material
Introduction
With the prospect of oil running out in about four decades[3] at the current rate of consumption, scientists are eagerly turning to new technology to solve an increasing demand for energy. A promising source is Hydrogen fuel cells. However, the biggest challenge to this is its storage[4]. Candidates need to have a high hydrogen density and ease of use at standard temperature and pressure.
Borazane is formed from the donation of the lone pair on nitrogen into the empty p orbital of boron. The resulting structure is similar to that of ethane.

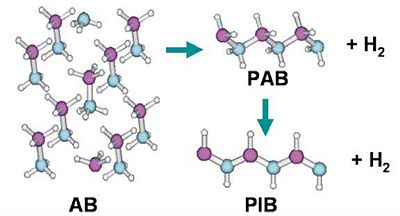
The release of hydrogen from borazane is through a polymerisation process where borazane is turned into polyaminoborane(PAB) and a hydrogen molecule. This can further polymerise to give polyiminoborane(PIB) and a second hydrogen molecule[5]. A diagram[6] illustrating this process is shown below:
Constructing the borazane molecule
Borazane can be constructed in a similar fashion to ethane. The major difference being the bond between nitrogen and boron having a greater ionic character than the carbon-carbon bond in ethane. The table below compares the bond lengths and internuclear angles with values found in the literature [7]
|
|
The values correlate well with the literature for this level of calculation. Increasing the complexity of the basis set would give a greater accuracy but would also take longer to compute. The .log file was examined to prove that the optimisation has converged.
The difference in energy between the staggered and eclipsed configuration of borazane is: 0.00326a.u. or 2.05kJmol-1 which compares to 0.00444a.u. or 2.78kJmol-1 for . So from this, we can see that the rotational barrier for borazane is less. If we compare this energy to that supplied by room temperature (RT=300*8.314=2.49kJmol-1) we can see that the barrier is lower than this energy.
The decrease in rotational barrier can be attributed to a decrease in sterics as the B-N bond distance is greater than the C-C bond distance in ethane (calculated at 1.54Å) and that the B-H and N-H bond distances are unequal so the H atoms are not perfectly aligned during the eclipsed state. The reasoning behind the increase in B-N bond length can be attributed to the ionic nature of the bond rather than the covalent nature seen in ethane's C-C.
A frequency calculation was run for both staggered and eclipsed. The staggered frequencies will be displayed in due course and the eclipsed output showed negative frequencies which is indicative of a transition state.
Due to time constraints, an NBO/charge distribution for the molecule could not be carried out but it can be predicted (and seen by the MO images further on) that most of the charge will be held by the electronegative Nitrogen.
The MO diagram of Borazane
An MO diagram of borazane was constructed using the MO for ammonia and a modified version for tetrahedral borane. The resultant molecule has the same point group as both tet-borane and ammonia: 'C3v
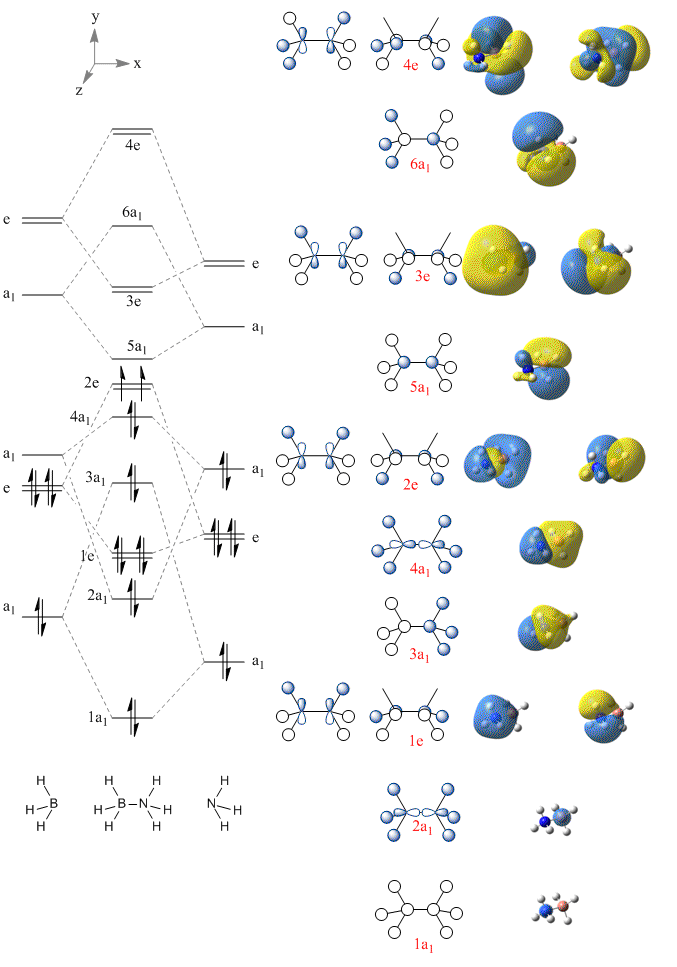
The qualitative orbitals (drawn in ChemDraw) show the different combinations of orbitals. The orbitals calculated with Gaussian however are erroneous, as they have been assigned incorrectly. The lowest energy MO is shown to have s character on the nitrogen and the next highest on the boron. However, the lowest should include the H s orbitals and have all the electron density being pulled in by the nitrogen. This image for the lowest orbital has actually been assigned 1e. Just to clarify, the above diagram is incorrect as the images of the core orbitals have shunted the images up by 2 orbitals.
Borazane Frequencies
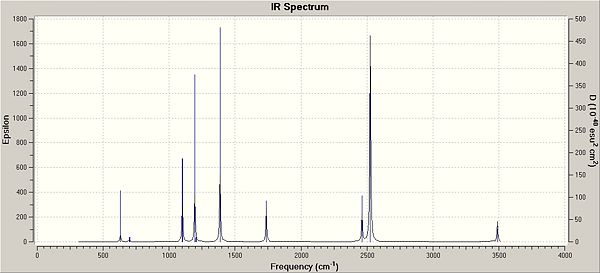
The I.R. peaks are compared to the literature values[8] below[9] and the N-H stretches are animated.
| Vibration Number | Frequency (cm-1) | Literature | Intensity |
|---|---|---|---|
| 631.39 | 727 | 18 | |
| 700.94 | 797 | 1.85 | |
| 701.72 | 797 | 1.854 | |
| 1100.55 | 1063 | 52 | |
| 1100.93 | 1063 | 52 | |
| 1194.52 | 1160 | 112 | |
| 1386.11 | 1369/1377 | 167 | |
| 1736.73 | 1599/1605 | 40 | |
| 2525.88 | 2276/2335 | 257 | |
| 3489.25 | 3195/3200 | 24 | |
| 3489.52 | 3308/3320 | 24 |
The stretches correlate well with those found in the literature.
Synthesis of Borazane
| Atoms | Energy/a.u. |
|---|---|
| Na+ | 162.08122881 |
| Cl- | -460.24873162 |
| NH4+ | -56.8860914 |
| BH4- | -27.24078368 |
| NaCl | -622.55076536 |
| Borazane | -83.19422687 |
Using the values obtained from the table above, the energy of the formation of borazane can be calculated. This comes from the equation:
NaBH4 + NH3Cl -> NH3BH3 + NaCl + H2.
Using E(Sum of product energies)-E(Sum of reactant energies) we find that the energy required to form borazane by the proposed method is -0.406a.u. which is -254.6kJmol-1, roughly the energy given off by the formation of a covalent bond.
A different method was tried in which all and all were put together in a 'one pot' optimisation. The energies of the products were found to be -706.96997695a.u. and those of the reactants -706.95006766a.u. which gives a difference of -0.01991a.u. or -12.4kJmol-1. The lower energy difference using this method comes from the overall energies of the atoms being lowered through geometrical optimisation. This way of modelling the reactions is chemically insignificant. Products energy:
Release the Hydrogen!
As borazane polymerises to form and , it releases hydrogen molecules by the following equation:
2Borazane -> PAB + H2 -> PIB + 3H2
The energy in going from 2 borazane molecules to releasing a hydrogen molecule can be worked out by finding the difference between the energies. This difference comes out to be -2.56kJmol-1. The energy difference going from PAB to PIB and giving off an extra two hydrogen molecules is -14.4kJmol-1. The overall energy difference, releasing three hydrogen molecules from two borazane molecules is -17.0kJmol-1. The negative value shows that it is a thermodynamically favourable process.
As the energy differences are not very large, they are easy to manipulate at around ambient temperature. This is critical and one of the biggest advantages of using borazane as a hydrogen storage material.
The one-pot optimisation as mentioned in the previous section gave an energy for as -166.39377058a.u. and as -166.41716939a.u. The energy difference between these two as two molecules of hydrogen would be recovered from the molecule is -14.7kJmol-1 which doesn't deviate too much from the previous value calculated at -14.4kJmol-1. The small decrease in energy can be attributed to a relatively insignificant geometrical optimisation by having the reactants and products in the same optimisation.
==References and project DOIs. Pheww, about time! == The DOI's have been dumped here and no effort (read lack of time) has been made to link them to the text.
| http://hdl.handle.net/10042/to-4657 |
| http://hdl.handle.net/10042/to-4658 |
| http://hdl.handle.net/10042/to-4659 |
| http://hdl.handle.net/10042/to-4660 |
| http://hdl.handle.net/10042/to-4661 |
And the .log files I calculated interactively can be found here File:Aaa207logfiles.zip
- ↑ S. Gierszal, J. Galica and E. Mis-Kuzminska; Physica Scripta.; 2003, 67, pp.525
- ↑ M.Y. Dorensbourg and D. J. Dorensbourg; J. Chem. Ed; 1970; 47; pp.33 DOI:10.1021/ed047p33
- ↑ http://www.bp.com/liveassets/bp_internet/globalbp/globalbp_uk_english/reports_and_publications/statistical_energy_review_2008/STAGING/local_assets/2009_downloads/statistical_review_of_world_energy_full_report_2009.pdf
- ↑ J. Wang on Petrovic & Mulliken, Sandia National Laboratories, 2003
- ↑ T. Autrey et al., Angew. Chem. Int. Ed.; 2005, 44, pp.3578
- ↑ http://www.aps.org/meetings/multimedia/upload/Overview_of_the_Hydrogen_Inititative_Dresselhaus.pdf
- ↑ C. R. Miranda and G. Ceder; J. Chem. Phys.; 2007; 126, pp.184703DOI:10.1063/1.2730785
- ↑ F. Cheng, H. Ma, Y. Li, and J. Chen; Inorg. Chem.; 2007; 46; pp.788 DOI:10.1021/ic061712e
- ↑ DOI:10.1002/anie.200801197
