Rep:Mod:Joelswiki

NH₃ molecule

NH₃ bond distance = 1.01798

NH₃ bond angle = 105.749°

Calculation Method: RB3LYP

Basis Set: 6-31G(d,p)

Final Energy = -56.55776873 a.u.

Point Group: C_3V

	Item	Value	Threshold	Converged?
Maximum	Force	0.000004	0.000450	YES
RMS	Force	0.000004	0.000300	YES
Maximum	Displacement	0.000072	0.001800	YES
RMS	Displacement	0.000035	0.001200	YES

NH3 molecule

The optimisation file is linked to here

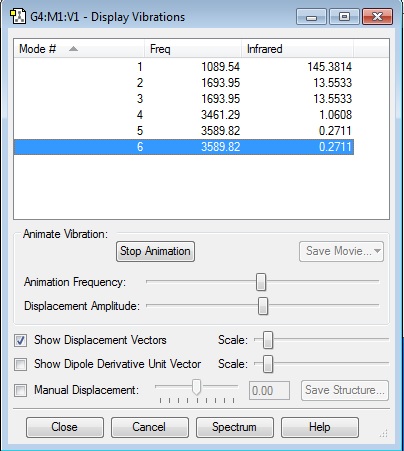
1. How many modes do you expect from the 3N-6 rule? Since N = 4, 3(4) - 6 = 6 modes expected

2. Which modes are degenerate (ie have the same energy)? Modes 2/3 and 5/6 are degenerate

3. Which modes are "bending" vibrations and which are "bond stretch" vibrations? Modes 1-3 are bends while 4-6 are stretches

4. Which mode is highly symmetric? Mode 4 (Symmetric bond stretch)

5. One mode is known as the "umbrella" mode, which one is this? Mode 1

6. How many bands would you expect to see in an experimental spectrum of gaseous ammonia? 2 bands. Mode 4,5,6 are weak signals and will not be clearly peaked in the spectrum. Of the remaining vibrational modes, one band will be from mode 1, while the other will be from the degenerate modes 2 and 3

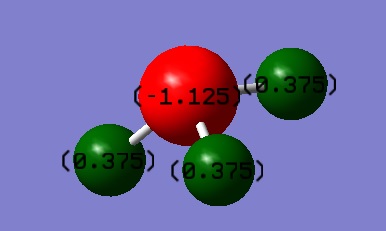
N: -1.125

H: 0.375

N is expected to have the negative charge as it is more electronegative than H, which is thus expected to have a positive charge

H₂ molecule

H₂ bond distance = 0.74289

H₂ bond angle = 180°

Calculation Method: RB3LYP

Basis Set: 6-31G(d,p)

Final Energy = -1.17853935 a.u.

Point Group: D_∞h

	Item	Value	Threshold	Converged?
Maximum	Force	0.000066	0.000450	YES
RMS	Force	0.000066	0.000300	YES
Maximum	Displacement	0.000087	0.001800	YES
RMS	Displacement	0.000123	0.001200	YES

H2 molecule

The optimisation file is linked to here

Vibrational mode: Bond stretch (4464.36 cm^-1). No bands will form on an IR spectrum (Infrared value of 0.000) as H₂ is a linear homodinuclear molecule with no net dippole moment.

N₂ molecule

N₂ bond distance = 1.10550

N₂ bond angle = 180°

Calculation Method: RB3LYP

Basis Set: 6-31G(d,p)

Final Energy = -109.52412868 a.u.

Point Group: D_∞h

	Item	Value	Threshold	Converged?
Maximum	Force	0.000001	0.000450	YES
RMS	Force	0.000001	0.000300	YES
Maximum	Displacement	0.000000	0.001800	YES
RMS	Displacement	0.000000	0.001200	YES

N2 molecule

The optimisation file is linked to here

Vibrational mode: Bond stretch (2457.33cm^-1). No bands will form on an IR spectrum (Infrared value of 0.000) as N₂ is a linear homodinuclear molecule with no net dippole moment.

Reaction energy of the Haber-Bosch process

N₂ + 3 H₂ --> 2 NH₃

E(NH₃)= -56.55776873 a.u.

2*E(NH₃)= -113.115537 a.u.

E(N₂)= -109.52412868 a.u.

E(H₂)= -1.17853935 a.u.

3*E(H₂)= -3.53561805 a.u.

ΔE= Energy of products - Energy of reactants =2*E(NH₃)-[E(N₂)+3*E(H₂)]= -0.05579095 a.u. = -146.48 kJ/mol (Literature value: -92.4 kJ/mol)

As the reaction is exothermic, the product(ammonia) is more stable than the reactants(nitrogen and hydrogen).

Choice of molecule: O₂

O₂ bond distance = 1.21461

Calculation Method: RB3LYP

Basis Set 6-31G(d,p)

Final Energy = -150.32004019 a.u.

Point Group: D_∞h

	Item	Value	Threshold	Converged?
Maximum	Force	0.000114	0.000450	YES
RMS	Force	0.000114	0.000300	YES
Maximum	Displacement	0.000069	0.001800	YES
RMS	Displacement	0.000097	0.001200	YES

O2 molecule

The optimisation file is linked to here

Vibrational mode: Bond stretch (1658.53 cm^-1). No bands will form on an IR spectrum (Infrared value of 0.000) as O₂ is a linear homodinuclear molecule with no net dippole moment.

Both O: 0.000 Net charge of 0 on both oxygen atoms is expected as O₂ is a linear, homodinuclear molecule and both atoms have the same electronegativity.

Molecular Orbitals

Spin: Triplet

3σ_g (bonding) orbital of oxygen formed by a head-on overlap between the 2p_x AOs from each oxygen atom. This orbital belongs to the valence shell (n=2), and thus is considerably lower in energy than the orbitals formed from the 1s orbitals, which are in an inner principal quantum shell

1π_u (bonding) orbital of oxygen formed by a side-on between the 2p_y AOs from each oxygen atom. For O₂, the π bonding orbitals should in principle be higher in energy (MO 5/6) than the σ bonding orbital (7) formed between p orbitals due to insufficient MO mixing, compared to N₂ where the σ bonding orbitals are higher in energy than the π bonding orbitals. However, this is not reflected in the MO calculation. This highlights that the calculations may not always be correct. (Refer to 'Extra Information')

1π_g* (antibonding) orbital of oxygen formed from the destructive interferance between the 2p_y AOs from each oxygen atom. This orbital is singly occupied, also known as the SOMO (Singly Occupied Molecular Orbital)

Another 1π_g* (antibonding) orbital of oxygen, but formed from the destructive interferance between the 2p_z AOs from each oxygen atom which are degenerate to the 2p_y one above, and is also a SOMO. As the two 1π_g* orbitals are degenerate and are singly filled, this makes oxygen a diradical that is paramagnetic, consequently, liquid oxygen is observed to be attracted under a magnetic field.

3σ_u* (antibonding) orbital of oxygen formed from the destructive interferance between the 2p_x AOs from each oxygen atom. This orbital is unfilled, and is also the (LUMO)Lowest Unoccupied Molecular Orbital

Extra Information

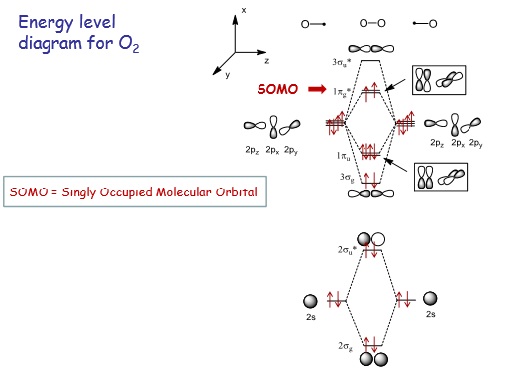
Credit: Prof. Ramon Vilar, Imperial College London
From the experimental MO diagram of O₂ the π bonding orbitals (1π_u) are higher in energy than the σ bonding orbital (3σ_g) as molecular orbital mixing is not significant enough to raise the energy of the 3σ_g orbital above the 1π_u orbital (as the 2σ_g and 3σ_g MOs are not close enough in energy). This is in contrast to the theoretically calculated MO from gaussian which puts the 3σ_g orbital at a higher energy level