Rep:Mod:Jazz0611-1

Computational project, Zain Khawaja

Introduction

Computational methods can be used to model aspects of organic chemistry. The information obtained can be used to rationalise the outcome of reactions as well as predict new type of reactions. In this case, the most likely product of the reaction is determined using molecular modelling, by obtaining the lowest energy conformation of a molecule (optimised geometry).

The Hydrogenation of the Cyclopentadiene dimer

Dimerisation of Cyclopentadiene

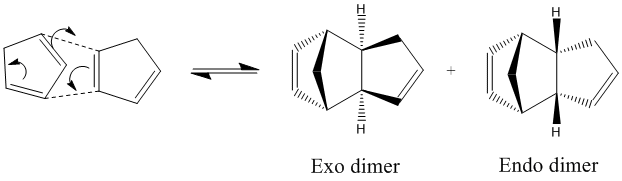
Cyclopentadiene spontaneously undergoes a Diels-Alder [4+2] cycloaddition to form the major endo dimer product and the minor exo dimer product depending on whether the reaction is under thermodynamic or kinetic control.

Fig 1: Dimerisation of Cyclopentadiene

Using an MM2 calculation run on ChemBio3D, the product geometries were optimised in order to determine which product is the lowest in energy and therefore the most thermodynamically stable. The results of the optimisation produces various energies for each product, including the total energy. The results are compiled in a table below:

Table 1

Energy / kcal/mol	Exo dimer	Endo dimer
Stretch:	1.2860	1.2558
Bend:	20.6031	20.8537
Stretch-Bend:	-0.8417	-0.8349
Torsion:	7.6544	9.5044
Non-1,4 VDW:	-1.4326	-1.5193
1,4 VDW:	4.2351	4.3029
Dipole/Dipole:	0.3773	0.4455
Total Energy:	31.8817 kcal/mol	34.0079 kcal/mol

The results show that the endo geometry has a higher energy than the exo geometry. In other words, if the reaction was under thermodynamic control, the exo dimer would be the major product since it is thermodynamically more stable product than the endo dimer. This can be explained by the unfavourable interactions between the two out of plane hydrogens and the bridged methyl group, which are only present in the geometry of the endo product. This unfavourable interaction experienced by the bridge head carbon also brings about the difference in torsional energy (1.85 kcal/mol) between the exo and endo dimer as seen in Table 1.

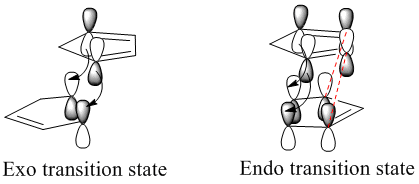
In actual fact, the endo dimer is the major observed product at room temperature. This indicates that the endo dimer is the kinetic product of the reaction. As stated earlier, the reaction proceeds by a Diels Alder style mechanism, so the two different products are brought about by two differing transition state orientations (differing approach of the reacting dienophile to the diene). By observing the secondary orbital interactions in the transition state of the endo dimer (interactions which are not present in the exo dimer transition state) we can observe how the endo transition state is stabilised relative to the exo transition state (endo rule):

Fig 2: Orbital interactions in the transition states

Hydrogenation of Cyclopentadiene dimer

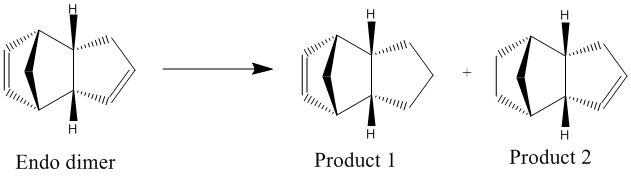
Partial hydrogenation of the endo cyclopentadiene dimer results in formation of two dihydro derivatives (Figure 3). Using an MM2 calculation run on ChemBio3D, the geometries of the two hydrogenation products were optimised to compute values for the total energy and other contributing energies. This allowed us to predict the preferred stereochemistry of the product. The values are given in Table 2:

Fig 3: Hydrogenation of the endo dimer

Table 2

Energy / kcal/mol	Product 1	Product 2
Stretch:	1.2659	1.1014
Bend:	19.8063	14.5486
Stretch-Bend:	-0.8276	-0.5458
Torsion:	10.8698	12.5055
Non-1,4 VDW:	-1.2207	-1.0836
1,4 VDW:	5.6394	4.4982
Dipole/Dipole:	0.1621	0.1407
Total Energy:	35.6953 kcal/mol	31.1651 kcal/mol

The results show that product 2 is lower in energy (thermodynamically more stable) than product 1 (by 4.53 kcal/mol), indicating that product 2 is the thermodynamic product and product 1 is the kinetic product. Moreover, this proves that hydrogenation of the double bond in the cyclohexane ring is easier than that of the double bond in the cyclopentadiene ring, provided there is enough energy to overcome the thermodynamic barrier.

The most significant difference in energy between the two molecules is the bending energy, where product 1 has a bending energy 5.26 kcal/mol higher than product 2 (i.e. more energy needed to distort product 1). Moreover, product 1 has greater torsional strain (smaller torsional energy as less energy needed to relieve the steric strain in the ring). These two energies are the highest contributors to the overall higher energy of product 1 and once again prove that hydrogenation of the double bond in the cyclohexane ring is easier as it results in the greatest release of steric strain and leads to the more stable thermodynamic product.

Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD⁺ analogue)

Reaction of Pyridinium Ring in N-methyl Pyridoxazepinone with a Grignard Reagent

Part 1

In this reaction, the optically active derivative of prolinol is reacting with methyl magnesium iodide, which has the effect of alkylating the pyridinium ring at the 4-position.

Table 3

	Energy (kcal/mol)	Dihedral Angle (o)
Conformer 1	44.25	24.67
Conformer 2	43.15	11.21
Conformer 3	43.11	10.45

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

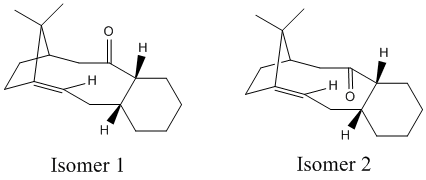
A key intermediate in the synthesis of Taxol contains stereochemistry where the carbonyl group can either point above or below the plane of the ring. This is an example of atropisomerism, where free rotation about a single bond is hindered due to steric demand, bringing about the possibility of multiple conformers. In this case, it is possible for the taxol intermediate to show this type of isomerism since free rotation is hindered by the rigidity imposed by the ring system and the carbonyl group. The two isomers are shown in Figure 4.

Fig 4: Atropisomerism shown by the two conformers of a taxol intermediate

The stereochemistry of carbonyl addition therefore is predominated by the lowest energy (and therefore most stable) isomer, thus the geometries of both isomers were minimised via an MM2 forcefield and MMFF94 forcefield using ChemBio3D and the most probable stereochemistry was investigated. The results are shown in Table 4.

Table 4

Energy / kcal/mol
Stretch:	2.6695	2.5601
Bend:	15.8480	10.7533
Stretch-Bend:	0.3878	0.3232
Torsion:	18.2861	19.6195
Non-1,4 VDW:	-1.1308	-1.3385
1,4 VDW:	12.6962	12.5472
Dipole/Dipole:	0.1438	-0.1835
Total Energy (MM2):	48.9006 kcal/mol	44.2813 kcal/mol
Final Energy (MMFF94):	70.538 kcal/mol	60.5648 kcal/mol

As can be seen from the results in table 4, both MM2 and MMFF94 minimisation energy calculations show that isomer 2 has the lower energy and is the more stable intermediate. This corresponds to when the carbonyl group is pointing down, below the plane of the ring. It was found that an initial MM2 optimisation gave a slightly higher energy conformer where the cyclohexane ring was arranged in a twist-boat conformation and thus to minimise the geometry further, the atoms were rearranged manually to product a chair conformation. This was minimised to give a lower energy intermediate and we know that the structures of both intermediates are the most stable in their own right since optimisation to the lowest energy brought about a chair conformation (present in both structures, which is the known minimum energy conformation. Although MMFF94 minimisation produces different energy values, it still reflects the same trend (isomer 2 is more stable) although the difference in energy values is higher for the MMFF94: 4.62 kcal/mol difference (MM2) compared with 9.97 kcal/mol (MMFF94).

We would assume, since a double bond positioned at a bridgehead carbon is relatively strained (as the double bond is positioned for isomer 1 and 2) that the alkene would be relatively reactive. However, this is not the case and hydrogenation of the alkene is quite a slow process. This decreased reactivity can be explained by the fact that the alkene functional group is positioned in a large ring and renders the alkene hyperstable. This hyperstability, brought about by the bridge head carbon, enforces increased strain in the parent saturated alkane compared with the alkene. Moreover, since formation of a strained tetrahedral structure from stable pyramidal geometry that is flat (twisting the alkene geometry) is energetically unfavourable, we predict a negative olefin strain energy.

Modelling Using Semi-empirical Molecular Orbital Theory: Regioselective Addition of Dichlorocarbene

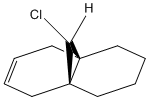
An improvement into our understanding of stereoselectivity may be obtained by illustrating the importance of electron influence on chemical bonds and spectroscopic properties. Previously, we obtained this understanding through a mechanical model but it is possible to also observe the electron distribution in molecular orbitals. The molecule that was studied for this exercise is 9-ChIoro-1,4,5,8-tetrahydro-4a,8a-methanonaphthalene and is shown in Figure 5. We consider the molecular orbitals to understand the regioselectivity of electrophilic addition to this dichlorocarbene.

Fig 5: 9-ChIoro-1,4,5,8-tetrahydro-4a,8a-methanonaphthalene

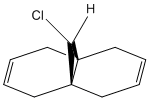
The molecule was minimised using an MM2 forcefield in ChemBio3D. This produced an energy of 17.9077 kcal/mol. The molecule can be visualised here:

A MOPAC/PM6 calculation was then run, which would provide an approximate representation of the valence-electron molecular wavefunction. This computed an energy of 19.7403 kcal/mol for the molecule. Moreover, the calculation allowed us to obtain a representation of the molecular orbitals. We expect that as this molecule contains a plane of symmetry that cuts through the chlorine atom, that the molecular orbitals should contain the same plane of symmetry, however for those defined by the PM6 MOPAC calculation, this was not the case. The calculations were repeated with a MOPAC/RM1 method and this produced much better results. These can be seen below:

HOMO-1

HOMO

LUMO

LUMO+1

LUMO+2

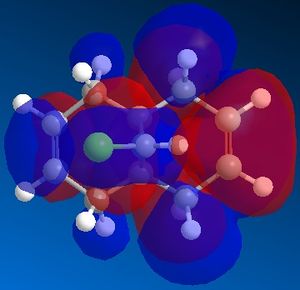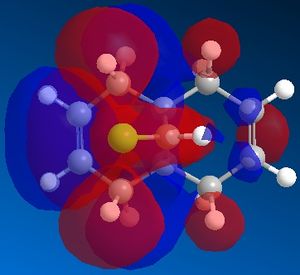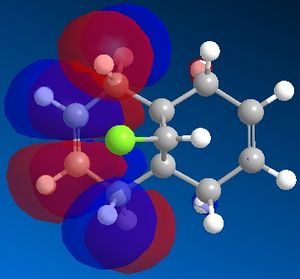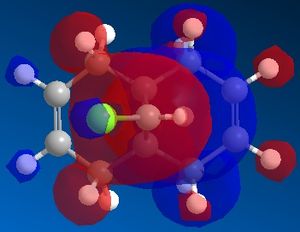We can explain the reaction of the dichlorocarbene molecule with electrophilic reagents by observing the orbitals above. By nature, we assume initially that electrophilic addition will take place at the most nucleophilic alkene. Examination of the HOMO shows that electron density is highest around the syn alkene relative to the chlorine and lower at the anti alkene relative to the chlorine. This indicates that the syn alkene relative to the chlorine is the more nucleophilic and thus more susceptible to attack by an electrophile.

In order to study the effect of the carbon-chlorine bond (C-Cl) on the vibrational frequencies of the syn diene, it was necessary to calculate the vibrational stretching frequencies of the diene and compare the values with those of the mono-hydrogenated derivative of the diene (hydrogenated at the alkene anti to the chlorine, Figure 6). This calculation required an optimisation and frequency method run on Gaussian.

Fig 6: Mono-hydrogenated derivative

Table 5 - Infra Red Stretching Frequencies

Molecule	C-Cl stretch /cm-1	syn C=C stretch /cm-1	anti C=C stretch /cm-1
	772.5	1760.9	1740.7
	780.0	1753.7	N/A

The results show that the C-Cl stretch appears at a different frequency depending on the molecule. We predict the C-Cl bond to be weaker for the diene since is has a lower frequency stretch. Moreover we can use the MOs we defined earlier to explain this theoretically. The anti double bond brings about a direct overlap between the C-Cl σ* orbital and the π orbitals, however this overlap has a destabilising effect due to the antibonding nature of the overlapping σ* orbitals. The destabilisation interaction causes a weakening of the bond strength and we see this as a decreased vibrational stretching frequency. Moreover, we see a higher stretching frequency for the hydrogenated product since this destabilising overlap is not present. The results also show that both molecules have a C=C stretch (for the syn alkene) at around 1760cm^-1. There is an absence of a C=C stretch for the hydrogenated product as it does not have an anti double bond. In the dichlorocarbene molecule, this anti C=C stretch appears at a lower frequency than the syn C=C stretch, confirming that it is a weaker bond (as we discussed earlier with respect to increased electron density at the syn alkene functional group).