Rep:Mod:Jas213TS

Transition Structures

The following computational experiment aims to characterise the transition structures present in the Cope rearrangement as well as the two transition structures of the Diels-Alder cycloaddition. All calculations and optimisations are based on the computed results using the Gauss View 5.0 programme. The key idea of what Gaussian does is to solve the Schrödinger equation to obtain the energy. GaussView proceeds assuming that no instantaneous pairwise interactions are included. Only single electron Schrödinger equations are used^[16].

The Cope Rearrangement Tutorial

Fig. 1 Cope Rearrangement

The Cope Rearrangement is a [3,3]-sigmatropic rearrangement (Fig. 1) of 1,5-hexadiene which was studied in the following tutorial.The free rotation along the $s{p}^3$-hybridised single bonds allows the existence of different conformers of the 1,5-hexadiene molecule which have been compared at the start. The Cope-Rearrangement is believed to proceed in a concerted fashion via either a chair or a boat transition.^[1] The chair TS lies slightly lower in Energy. However, it is still ambiguous which transition state is formed preferentially. The geometries and energy minimas of the different transition structures were analyzed to quantify this difference eg. activation energies.

Throughout this first Tutorial part, the method used to solve the Schrödinger equation was either Hartree Fock (HF) or the less approximate Density Functional Theory (DFT) method. The mathematical description of the wave function based on the atomic orbitals, hence the basis sets used were either 3-21 or 6-31*.

Hatree-Fock: Key breakthrough $\hat{F}(1)={\hat{H}}^{core}(1)+\sum _{j=1}^{n/2}[2\hat{J}(1)-\hat{K}(1)]$

$\hat{F}(1)$: one-electron Fock Operator

${\hat{H}}^{core}(1)$: one-electron Hamiltonian Operator (KE, nuclear attraction)

$\hat{J}(1)$: Coulomb Operator (PE)

$\hat{K}(1)$: Exchange Operator (antisymmetric wave function w.r.t. electron exchange)$2^{}$

$2^{}$

When two reactant molecules approach each other, the energies of the starting materials are known fairly well. However, it is sometimes hard to estimate the energy of the transition state. Coulson and Longuet-Higgins had the idea to estimate the energy of the transition state by treating the interaction between the two reactant molecules as a perturpation on each other. This is called perturbation theory. This approach leads to the same bonding/antibonding interactions as if we were simply forming a bond. The crucial difference is that our two reactant molecules now come from far apart to bonding distance. However, as the reactant molecules approach the perturbation only increases until at a certain point, other factors come into play and this theory fails to accommodate such a large change. This makes it difficult to have a clear picture of the transition state.^[11] The QST2 method and the IRC method are presented in the following. Especially, the IRC method uses this idea of infinitely apart reactant molecules.

Nf710 (talk) 12:19, 25 February 2016 (UTC) This is an interesting intro you have posed some interesting points in your intro. You have shown a good understanding of HF however that equation is just for the ground state. you could have perphaps gone into some more detail but it is still pretty good.

Optimising the Reactants and Products

Fig. 2 Newman projections

1,5-Hexadiene (Anti1 Conformation)

The reactant, 1,5-Hexadiene, has sp³-hybridised carbon atoms and can hence exist in various conformations. These are examined here. The antiperiplanar conformer (dihedral angle: 180°) of 1,5-hexadiene was built and the clean function was used, to generate a more chemically intuitive version of the molecule in question. Then, the molecule was optimized using Hartree-Fock method and the 3-21G basis set. The Energy of the molecule was measured and the log.file was checked to see whether all the forces had converged. The Energy and Pointgroup obtained can be found in the following table (File:ANTI1.log).

Table 1. Anti1 Conformation

Structure	Electronic Energy/Hartrees	Point Group
	-231.69260235 a. u.	C3

1,5-Hexadiene (Gauche1 and Gauche2 Conformation)

Now draw another molecule of 1,5-hexadiene with a "gauche" linkage for the central four C atoms. Would you expect this structure to have a lower or a higher energy than the anti structure you have just optimized? Optimize the structure at the HF/3-21G level of theory and compare your final energy with that obtained in (a). Again, check if the molecule has symmetry and make a note of the point group.

The two gauche conformers were built by choosing a dihedral angle of 60°. They are both higher in Energy than the previously analyses anti1 structure. This increase in energy was expected due to the steric clash of the two alkene substituents. Optimisation (HF/3-21G) followed by "Symmetrise" lead to the minimum energy of the gauche conformer 1 to be slightly lower than gauche conformer 2. This seems reasonable due to the decreased steric clash observed for gauche conformer 1, where the alkene ends point away from each other instead of towards each other (gauche conformer 2).

File:Gauche1 jas.log File:React Gauche2 jas.log

Table 2. Gauche1 and Gauche2 Conformation

Structure	Electronic Energy/Hartrees	Point Group
Gauche conformer 1	-231.69153032 a. u.	C2
Gauche conformer 2	-231.68771616 a. u.	C2

1,5-Hexadiene (Gauche3 Conformation)

File:Output 3.chk File:Gauche 3.log

The third gauche conformer has the lowest energy minimum, which is even lower than for the anti1 conformer. How is this possible? It can be explained by looking at the MO representation of the gauche3 molecule. The MOs show a stabilising interaction between the two double bonds (red), which cannot be seen in the antiperiplanar structure. Because of this extra secondary orbital stabilizing interaction (Fig. 3), this conformer is lowest in Energy. Thus, the two unsaturated alkene bonds do not result in a steric clash anymore, but in a lowering of the energy. However, this loss of steric clash causes a decrease in the level of symmetry. The point group is now C1. The output log file had a dihedral angle of 67.68 degrees.

Nf710 (talk) 12:27, 25 February 2016 (UTC) Good use of orbitals to show the ordering in energy.

Table 3. Gauche3 Conformation

Structure	Electronic Energy/Hartree	Point Group	MO analysis
Gauche conformer 3	-231.69266120 a.u.	C1	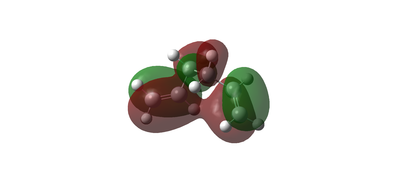Fig. 3 MO analysis

Comparison with Appendix 1 (Script)

The anti1 conformer optimised at the very beginning, is identical to the anti1 conformer in Appendix 1. This can be verified by their simliar energy minima. The gauche conformer 1 optimised (Table 2) is identical to gauche 2 in Appendix 1 and the gauche conformer 2 optimised in Table 2 is identical to gauche1 in Appendix 1. They show similar energetic minima and geometric structures.

1,5-Hexadiene (Anti2 Conformation)

The 1,5-Hexadiene anti2 conformation was optimised using the Hartree-Fock method and 3-21G basis set. The molecule was then symmetrised with relaxed tolerance. The energy minimum obtained via this optimisation was -231.69253528 au (or Hartrees) and hence in good agreement with the value shown in Appendix1. The point group is $C_i$, thus there is a centre of inversion. File:Anti2 3.log

Comparison between HF/3-21G and B3LYP/6-31G(d)

The Anti2 Conformer was subsequently re-optimised using a higher level of theory and a larger basis set (DFT, B3LYP/6-31G(d))File:ANTI2 DFT.log. The calculated energy was: -234.61171166 a. u. To make sure that the minimum was found, an additional frequency analysis was performed and positive/real vibrational modes were obtained. It is meaningless to compare this value with the previously obtained Energy value, because they were obtained via different basis sets and different levels of theory! Nonetheless, the geometries of the structures could be compared and can be found in the table below.

As can be seen from the table, DFT is generally more precise, because in this case a more expansive basis set (6-31G(d)) is used, giving a more precise picture of the MOs. Thus the overall energy is closer to the true energy of the system. Additionally, DFT takes correlation effects (spin and pairing energy) into account. The Hartree-Fock method, on the other hand, only uses a single slater determinant to solve the many electron Schrödinger equation_[3]. The slater determinant can become very hard to solve at larger basis sets. Another drawback of the HF is, that it overestimates the electronic repulsion term as a function of the mean field, because it does not consider is that an "electron will push away the other electrons as it moves around"^[4].

Concerning the cost of DFT calculation, the scaling is an important factor and refers to how time increases with size, but says nothing about the absolute amount of time for a given molecule. Gaussian is a programme which uses approximately the same algorithms and routines for DFT and HF calculations. Therefore, the cost of a DFT calculation on a typical, moderately sized molecule (~10 heavy atoms), is double that of the HF calculation with the same basis set. For larger systems this should improve due to more favorable scaling.^[5]

In addition, a frequency calculation was also carried out in order to confirm we have located an energy minimum by ensuring all vibrational frequencies in the molecule are positive and real numbers. A Transition state and a critical point can be distinguished by the fact that the Transition state has one negative frequency, whereas for the energetic minimum only shows positive vibrational modes.

Table 4. Anti2 Conformation

Structure	Electronic Energy/Hartree (HF/3-21G)	Electronic Energy/Hartree (B3LYP/6-31G*)	Point Group
Anti 2 conformer	-231.69253528 a.u.	-234.61171166 a.u.	$C_i$

The overall geometry change of the anti2 conformation, optimised via the two different methods,can best be analysed by measuring the bond distances and dihedral angle. The table shows that there is only a minimal discrepancy between the two geometries, which indicates that a more sophisticated method does not necessarily give much better results, but a higher computational cost. The point groups were identical too. Therefore, the difference in energy between the two optimised results is the key advantage of the more sophisticated method. We can imagine the difference between HF/3-21G and B3YLP/6-31G* as the depth on a PES. The locations of these molecules are the same, because less precise basis sets give similiar results.

Table 5. Anti2 Geometry Analysis

Method	Dihedral angle C2-C3-C4-C5	Bond length C1-C2	Bond length C2-C3	Bond length C3-C4	Bond length C4-C5	Bond length C5-C6
HF	-179.9996°	1.31614 Å	1.50893 Å	1.55280 Å	1.50893 Å	1.31614 Å
DFT	180.0000°	1.33350 Å	1.50420 Å	1.54816 Å	1.50420 Å	1.33350 Å

Frequency Calculations

The frequency calculation can be used to characterize whether the minimum has been found. It is a minimum if it possesses real and positive vibrational frequencies only. From the IR spectrum, it can be seen, that this is the case. There is no negative/imaginary frequency that could indicate, that we have not found the desired state. Additionally, it is worth noticing the C-H stretches at $3000-3250c{m}^{-1}$ indicating sp² and sp³ stretches. Furthermore, the strong peak at approximately $950c{m}^{-1}$ indicates a CH₂ wag.

By looking at the Thermochemistry section in the log file, the following information was obtained: The sum of electronic and zero-point-Energies is the lowest possible Energy state at 0K the given compound can adopt and accounts for remaining vibrational energy. Comparison between the sum of electronic and zero-point-Energies and the sum of electronic and thermal energies shows a marginal difference, even though the latter was calculated at 298.15 K and 1 atm. The slight increases results from the fact that at this temperature, translational, rotational and vibrational contributions have to be taken into account, increasing the overall energy of the system. Gaussian operates by using the partition functions based on statistical thermodynamics to calculate all these properties.

Sum of electronic and zero-point Energies $E_{OK}=E_{el}+ZPE$

Sum of electronic and thermal Energies $E_{298K}=E_{el}+E_{vib}+E_{rot}+E_{trans}$

Sum of electronic and thermal Enthalpies $H=E+RT$

H: Enthalpy E: electronic Energy RT: thermal Energy (R=Ideal Gas constant, T=Temperature in K) At O K, RT=0 Thus: H=E

Sum of electronic and thermal Free Energies $G=H-TS$

The use of the Gibbs Free Energy implies constant pressure.

all Energies in Hartree/Particle:

Table: Thermochemistry section

Zero-point correction	Thermal correction to Energy	Thermal correction to Enthalpy	Thermal correction to Gibbs Free Energy
0.142497	0.149845	0.150789	0.110912
Sum of electronic and zero-point Energies	Sum of electronic and thermal Energies	Sum of electronic and thermal Enthalpies	Sum of electronic and thermal Free Energies
-234.469215	-234.461866	-234.460922	-234.500800

Nf710 (talk) 12:55, 25 February 2016 (UTC) Good underdtanding of the thermochemistry data. and what they mean.

Optimising the "Chair" and "Boat" Transition Structures

In the following the two

In this tutorial section, the Chair and Boat transition structures were found and optimised via several methods:

• Calculating the force constants
• Frozen coordinate method
• QST2 method
• Intrinsic Reaction Coordinate (IRC) method

Finally, the activation energies were calculated.

Calculating the force constants

File:Chair TS optfreq.log

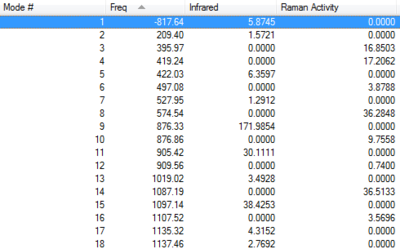
Initially, the guessed structure of the allyl fragment was drawn in Gauss view and optimised using the simple HF/3-21G method. The optimised fragment was pasted twice into a new file, the two fragments were arranged so that they would closely resemble the Chair TS with their terminal carbons being approximately 2.2 Å apart. Subsequently, the guessed Chair TS was optimised (TSBerny) and the frequencies were calculated. For the optimisation to be successufl, it is important that the TS guess represents the real TS as closely as possible. The frequencies obtained were all real and positive except for the one imaginary frequency, which indicated that the transition state had been found. The vibration which corresponds to the Cope rearrangement is the only negative vibration found at -817.64 cm^-1. (See table below).

Why does the imaginary frequency correspond to the transition state? A transition state possesses an imaginary frequency because the force constant is negative, resulting from the fact that displacement and force are opposing each other. This idea stems from the 1D harmonic oscillator where the angular frequency is determined by $\omega =\sqrt{\frac{k_f}{m}}$, if now $k_f$ is negative. The frequency becomes imaginary. To better illustrate what this imaginary frequency represents one has to know that on a potential energy surface(PES), a transition state corresponds to the first order saddle point. Meaning that in one direction in the nuclear configuration space the energy tends to a maximum while in all other orthogonal directions in the nuclear configuration space, the energy is a minimum.^[6] This downwards movement results in a negative second order derivative of the PES at this point.

Nf710 (talk) 13:00, 25 February 2016 (UTC) very good understanding

Frequencies	-817.64 cm-1	Energy/Hartrees
		-231.61932195 a.u.

Frozen Coordinate Method

File:CHAIR TS DERIVATIVE JAS.LOG

When the distance between the two fragments within the guessed Transition structure is too large, the optimisation will not be successful. This is the point when this method comes into play because you can fix the coordinates of the terminal carbon atoms to maintain a constant distance between the two fragments. Now during the optimsation, these terminal carbons are frozen whilst the remaining atoms are all minimised. When optimising the chair TS, the distance between the two fragments was held at 2.20 Å. The optimisation method used to minimise the energy was the simple HF/3-21G. Subsequently, the molecule was reoptimised by using the TS Berny optimisation. As previously, an imaginary frequency has been found, proving the successful termination of the optimisation to a transition structure. Comparing the resulting energy with the one above, suggest that the guessed structure was reasonable close to the TS, leading to a 0 % difference between the two energies.

Frequencies	-817.88 cm-1	Energy/Hartrees
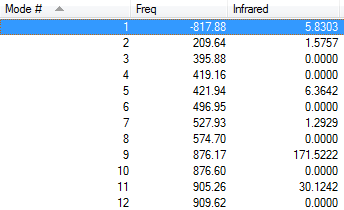		-231.61932232 a.u.

QST2 method

File:Boat TS QST2 JAS.log

"The Synchronous Transit-Guided Quasi-Newton (STQN) Method, developed by H. B. Schlegel and coworkers, uses a linear synchronous transit or quadratic synchronous transit approach to get close to the quadratic region around the transition state and then uses a quasi-Newton or eigenvector-following algorithm to complete the optimisation."^[7] This method converges efficiently to the actual transition state using an empirical estimate of the Hessian. Note that the difference in QST2 and QST3 is that the former requires two molecule specifications, whereas the latter requires three: reactant, product and TS in this order.

In this example the Boat Transition Structure was found by interpolating the structure of the reactant with the structure of the product. For this method to be successful, every atom (including hydrogens!) has to be numbered in the same way in the product and the reactant molecule. If these were inconsistent, GaussView was not able to track the movement of the atoms. The dihedral angle of the reactant and the product molecule was set to 0°, the inner bond angles across the two central carbons were set to 100°. The method proved to be very successful and the results using QST2 can be seen below. However, the QST3 method proved to be much more challenging and did not lead to any usable output, which is why no successful results can be presented.

Frequencies	-840.02 cm-1	Labelled Reactant & Product	Animation
			QST2 method:Please click to play

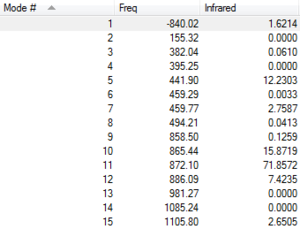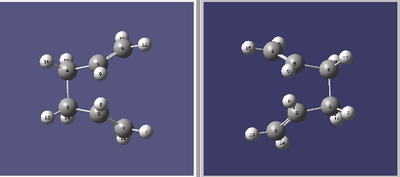
Intrinsic Reaction Coordinate (IRC) method

File:ChairIRCjas.log

The IRC method is used to predict the conformer the transition structure leads to. This is done by following the minimum energy path from the Transition structure to a local minimum on PES. During this process a series of small geometry steps in direction towards the conformer is performed by always followin the path where the gradient of the PES is steepest. Please note, an intermediate and product both show a zero gradient in the gradient along IRC plot.

The IRC method was used, specifying that the force constants are computed at every step. The IRC was set to 50 steps, it converged at 44 steps to a minimum energy of -231.69157903 a. u. This energy is closest to gauche conformer 2 and 4 in Appendix 1. The pointgroup of the conformer where the energy converged (step 44) had C2 symmetry and thus could technically correspond to both gauche2 and gauche4 conformers. This assumption was verified by optimisation of the step44 structure via HF/3-21G. An energy of -231.69166702 a. u. was obtained which showed that the minimum energy is closest to the gauche2 structure in Appendix 1.

Nf710 (talk) 13:03, 25 February 2016 (UTC) Correct structure well done

Energy along IRC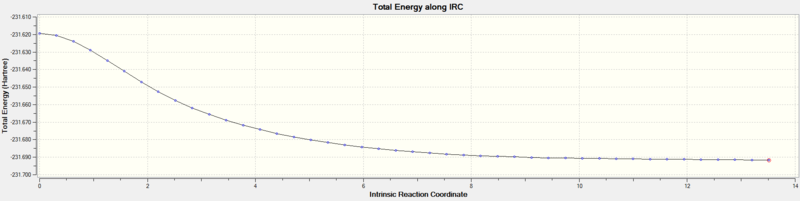
Gradient along IRC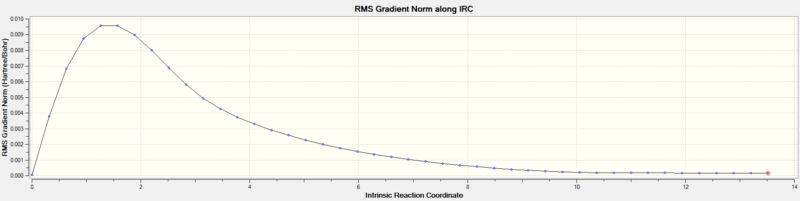
Reaction Pathway	Chair TS

Calculation of Activation Energies

The Activation Energies were calculated from the difference between the Sum of electronic and zero-point energies at 0 K of either the Chair or the Boat TS and the Sum of the electronic and zero-point energies of at OK of the reactant. The same procedure was performed for the Sum of electronic and thermal energies. The result was multiplied by 627.509 kcal/mol to obtain the activation energies in kcal/mol. Subsequently, the percentage error was calculated by using the experimental values given in the script. It can clearly be seen that, apart from one pecularity for the actiavtion energy of the boat TS (HF/3-21G), the results obtained with the B3LYP/6-31G* method are much closer to reality than for the HF/3-21G method used (Percentage errors). However, when we look at the geometry of the Transition States, the two methods used do not show large differences. Therefore, the simple HF/3-21G method is a nice and cheap first way of drawing the PES surface with the correct geometries, the B3LYP/6-31G* method adds the necessary depth to the PES surface by calculating the more exact energies.

To conclude, the lower activation energy is found for the antisymmetric chair. Thus the Cope rearrangement, the 3,3-sigmatropic rearrangement in hexa-1,5-diene proceeds more easily via the 4-memebered chair like transition state than via the 6-membered boat-like transition structure. Concerning the orbital symmetry, the boat transition structure (S) is symmetric with respect to a mirror plane of the boat structure. The Chair transition structure is hence antisymmetric with respect to this plane.

Summary of energies (in hartree)

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.61932195	-231.466700	-231.461340	-234.55692723	-234.414912	-234.408982
Boat TS	-231.60280249	-231.450929	-231.445300	-234.54309307	-234.402342	-234.396008
Reactant (anti2)	-231.692535	-231.539539	-231.532566	-234.611710	-234.469203	-234.461856

*1 hartree = 627.509 kcal/mol

Summary of activation energies (in kcal/mol)

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.	Percentage Error HF/3-21G	Percentage Error HF/3-21G	Percentage Error DFT/6-31G*	Percentage Error DFT/6-31G*
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K	at 0 K	at 298.15 K	at 0 K	at 298.15 K
ΔE (Chair)	45.71	44.69	34.06	33.18	33.5 ± 0.5	36 %	33 %	1.7 %	0 %
ΔE (Boat)	55.60	44.69	41.96	41.32	44.7 ± 2.0	24 %	0 %	6.1 %	7.6 %

Comparison of Geometries

	CC distance between fragments CHAIR TS/Å	CC distance between fragments BOAT TS/Å
HF/3-21G	2.02035	2.13977
B3LYP/6-31G*	1.96617	2.20661

Distances measured between the terminal carbons of the two fragments. All distances are given in angstroms.

Nf710 (talk) 13:07, 25 February 2016 (UTC) A very good report everything is written clearly and is easy to understand. you have come to the correct clusions. The lower basis gives the good geom approximations but not energies. you could have gone into more detail in the theory though. but still very good first section

Diels-Alder Cycloaddition

The pericyclic DA cycloaddition has been studied in the following with focus on the formation of cyclohexene from cis-butadiene and ethylene and the predominant formation of cis-5-Norbornene-endo-2,3-dicarboxylic anhydride over its exo counterpart. To explain the endo selection rule, the MOs as well as the activation energies of the transition states were analysed. The method used throughout this part is semi-empirical/AM1. AM1 stands for Austin Model 1, quantitative quantum mechanical molecular model for chemists, better than any ab initio methods, because it gives sufficiently accurate and is applicable to a specific molecule rather than being confined to simple models. The Austin model 1 evolved from MNDO, which overestimated repulsions between atoms when approx. their van der Waals distance apart. AM1 managed to overcome this MNDO weakness for hydrogen bonds without any increase in computing time.^[10]

Cis-Butadiene and Ethene Transition State

Woodward-Hoffmann FMO analysis

̪

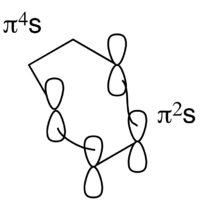
For a thermal pericyclic reaction, the Woodward-Hoffmann Frontier molecular orbital (FMO) analysis is shown above. From the drawing shown, it can be seen whether the two fragments are antarafacial (a) or suprafacial (s). Then, the following formula has to equal an odd number, for the reaction to be W-H thermally allowed:

$(4q+2{)}_s+(4r{)}_a=$ odd

Only the π²s fragment has the right number of electrons (if q=0). The π⁴s cannot be considered.

Thus:

$(4q+2{)}_s+(4r{)}_a=1$

The number obtained is odd, the reaction between cis-butadiene and ethene is therefore W-H thermally allowed. Note that "forbidden" does not necessarily mean that a reaction does not take place. "It only states taht the interaction of the orbitals presents an energy barrier, which the "allowed" reaction does not have."^[11]

Calculating the force constants

Cis-butadiene and ethene have been composed using the AM1 semi-empirical method. Cis butadiene showed a $C_{2v}$ symmetry, as it was drawn (dihedral angle of 0°). Please refer to the HOMO and LUMO MOs of the two reactants given in the table below (Table 1). The HOMO of cis-butadiene is clearly antisymmetric along the CC bond axis; and the cis-butadiene LUMO is symmetric with respect to the reflection plane. Therefore, in a concerted Diels Alder cycloaddition, the HOMO of ethylene and the LUMO of butadiene, both s symmetric with respect to the reflection plane and the LUMO of ethylene and the HOMO of butadiene are both a. Thus it is the HOMO-LUMO pairs of orbital that interact, and energetically, the HOMO of the resulting adduct with two new σ bonds is a. Therefore, in a concerted Diels Alder cycloaddition, it is the HOMO of ethylene and the LUMO of butadiene, both s symmetric with respect to the reflection plane and the LUMO of ethylene and the HOMO of butadiene are both a. If there was an electron withdrawing group on the ethene molecule, this would lower the Ethene's LUMO energy and lead to an even larger splitting and hence better overlap of the two orbitals. However in this case, with no substituents, the normal electron demand is usually assumed. According to Woodward-Hoffmann rules and in the case of the usual normal electron demand, the HOMO of cis-butadiene (antisymmetric) and the LUMO of ethene (antisymmetric) come together and form the HOMO of the transition structure of the adduct (antisymmetric, table 3). This reaction is allowed by Woodward-Hoffmann rules because the symmetry is preserved and the addition results in a decrease of the overall energy.

The Transition Structure was located subsequently. The optimised reactants were arranged in an envelope type structure at a distance of exactly 2.20 Å to maximise the overlap between the orbitals. Thus the overall symmetry was $C_s$. The Transition state was optimised by using the TS Berny method and performing a frequency analysis by calculating the force constants at any time File:DIELSALDERGUESS.log̪File:DIELSALDEROPT3.log̪. The minimum energy was found to be 0.1165465 Hartrees and the vibrations have been found to be real and positive except for one (Table 2).

Table 1. MO Analysis of the Reactants

HOMO cis-Butadiene	LUMO cis-Butadiene	HOMO Ethene	LUMO Ethene
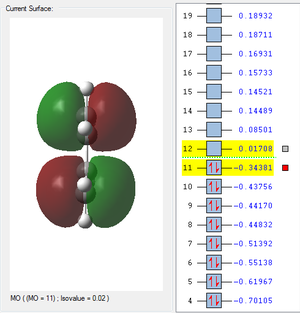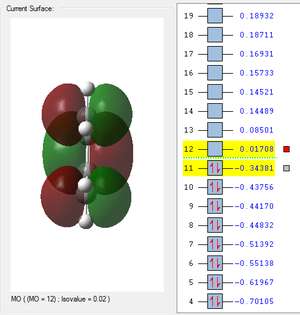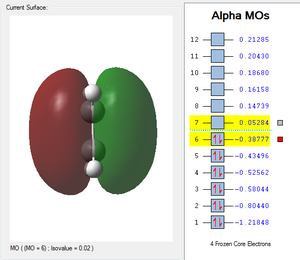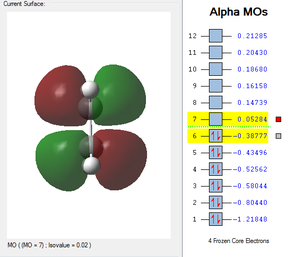Antisymmetric	Symmetric	Symmetric	Antisymmetric

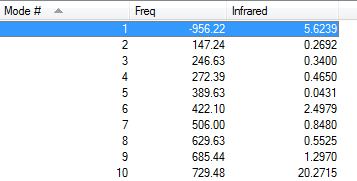
By looking at the imaginary frequency, one can clearly see that both bonds are formed synchronously and we can even see that the bonds are broken and formed at the same time. Thus the reaction is concerted. Furthermore, when looking at the first positive vibration, the vibrational mode looks very similar to an asynchronous rock (147.24 cm^-1). The LUMO and the HOMO of the two reactants have been given to determine whether this reaction proceeds via a normal or inverse electron demand. The HOMO of the diene is higher in Energy than the HOMO of the dienophile (ethene). Hence, this Diels alder reaction is normal electron demand. Vibrations shown confirm that the right transition structure was found. The transition structures show a bond length between the diene and the dineophile of 2.11927 or 2.11928 depending on the guess (log file) used. This means that the bonding interaction lays in between a bond length which would be an interatomic distance of sp³-hybridised carbon atoms 1.54 Å, but it is still smaller than the sum of the Van der Waals radii (carbon 1.70 Å) indicating some sort of bonding behaviour between the two reactants. The resulting point group of the Transition state was always found to be $C_s$.

Table 2. Frequency analysis

Vibrations	-956.22 cm-1	147.24 cm-1	Energy/Hartrees
			0.11165465 a.u.

Table 3.MO Analysis of Transition Structure

HOMO TS	LUMO TS	Animation
		Diels Alder Reaction Pathway - Please click to play

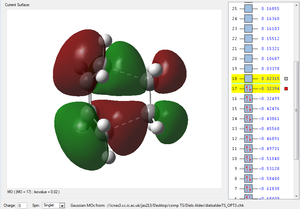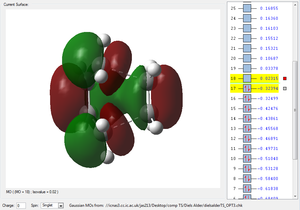IRC method

File:IRC DA jas.log

The Internuclear reaction Coordinate method was used to locate the transition state along the IRC. The IRC output was obtained from the chk file for the optimised Diels Alder transition structure. This was used to perform an IRC for 100 steps in the forward and the reverse direction. The reaction had to be calculated in both directions, because the reaction coordinate is not symmetrical and the force constant were always calculated. The IRC converged after 87 steps.

The given IRC plot showed the reaction in the reverse direction, from products to reactants. However, this does not change anything, since we are mostly interested in the TS Energy with respect to the Energy of the reactants and product. It can clearly be seen that the TS is much closer to the reactants across the IRC axis. Therefore we observe a so called "Early Transition State". According to Hammonds Postulate this means that the TS resembles the reactants and the reaction is exothermic. The energy of the reactants (last step) was found at 0.07462762 a.u. and the energy of the product (first step) at -0.01099166 a.u.

Energy along IRC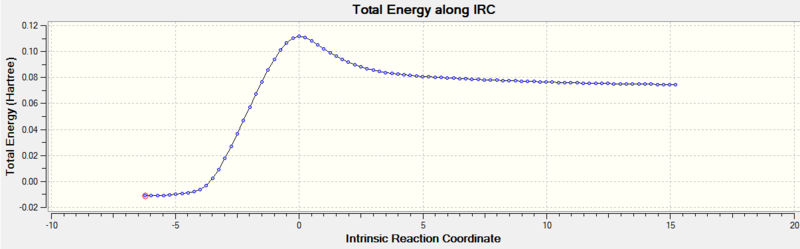
Gradient along IRC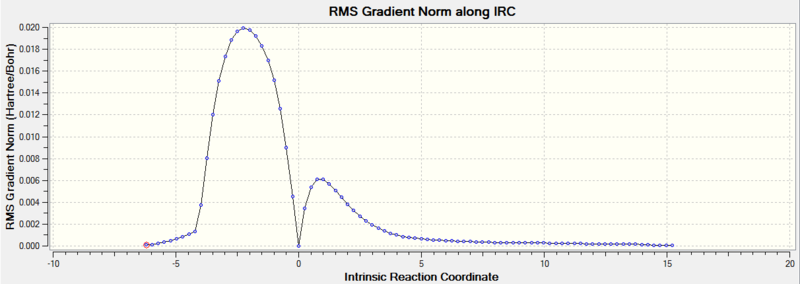
Reaction Pathway	Please expand for animation

The Regioselectivity of the Diels Alder Reaction

In case of maleic anhydride and cyclohexadiene as the reactants, the electron demand can be predicted much more easily. The dienophile now possesses an electron withdrawing group lowering its LUMO, leading to a better overlap with the HOMO of the diene which has "alkyl substituents" (only secondary carbons involved) leading to an increase in the energy of the diene HOMO. Therefore, the HOMO and the LUMO of the two reactant molecules are closer in energy, leading to a larger splitting. This reaction is exemplary for normal electron demand. Additionally, due to the ring structure of the diene, the desired s-cis conformation is maintained throughout and it does not need to adopt the right conformation before reacting with the other reactant. This facilitates the reaction to a great extent.

Having specified the electron demand and the reactant orbitals interacting in the following. We still have to ask ourselves which way round the two reactants approach each other. Approaching each other at a distance larger than an internuclear distance, in the approach trajectory, the question is whether the diene sits on top of the carbonyl end of the maleic anhydride (directly align with each other) or whether the two compounds point away from each other (staggered with respect to each other). The next to sections are dedicated to this question and to the optimisation of both transition structures. In other words, the basis for the Alder endo-rule is found via computational methods.

The endo product

Calculating the force constants

File:DIELSALDERENDO.log

The diels alder endo product was drawn on GaussView on the basis of the transition structure obtained above. The bond length of the two CC bonds which form the two new σ bonds during the reaction were elongated to 2.20 Å, an Optimisation+Frequency analysis was performed using TSBerny (semi-empirical/AM1) and calculating the force constants at all times.The transition structure obtained showed only one imaginary frequency and real frequencies for all the remaining vibrational modes. The imaginary frequency clearly showed the concerted movement of the Diels Alder cycloaddition.

Vibrations	-806.39 cm-1	62.43 cm-1	Energy/Hartrees
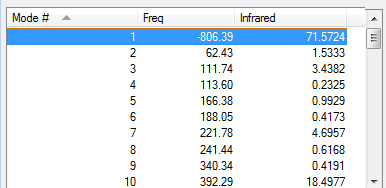			-0.05150480 a.u.

The QST2 method

File:Endo qst2 jas.log

The QST2 method was used to find the Endo Transition State. The geometry of the endo transition structure can be found in the table below; the interfragmentary distance C16-C1 is given by the distance between C1 and C16. This distance lays again in between the sp³-hybridised interatomic distance (1.54 Å) and the sum of the VdW radii (3.4 Å), indicating an interaction, but not a real bond. All other bond distances lay in between the sp3-hybridised CC bond length (154 pm) and the sp²-hybridised CC bond length (134 pm).

Reactants	Product

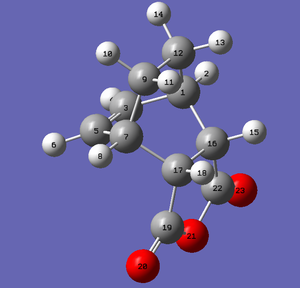Bond	C17-C16	C16-C1	C5-C3	C1-C12	C9-C12
Bond length/Å	1.40845	2.16298	1.39730	1.49046	1.52294

Vibrations	-806.18 cm-1	62.41 cm-1	Energy/Hartrees
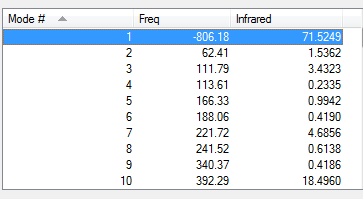Figure 14: Vibrations of the TS(Berny) Optimised Envelope Structure			-0.05150436 a.u.

MO analysis of the endo TS

As indicated in the table below, the HOMO as well as the LUMO of the endo TS are antisymmetric. The most important observation is the large secondary orbital interaction between the two approaching fragments due to the desired stabilising interaction between the π orbitals of the double bond and the π* orbitals of the C=O bonds. This stabilising interaction even outweighs the fact that the endo structure is more strained. Overall the endo Transition State is lowered due to this secondary overlap interaction. Consequently, the endo product is the kinetic product. As shown in the following exo TS analysis, no such stabilisation can be found, which results in a higher TS and thus the Exo product is the thermodynamic product (less strained product, lower in Energy). Furthermore, the endo transition state is believed to be stabilised not only due to orbital interactions, but also dipolar and Van der Waals interactions.

Table. HOMO & LUMO of the Endo product

HOMO	LUMO	Orbital Energies
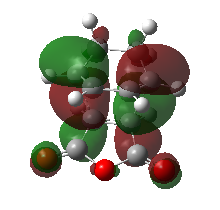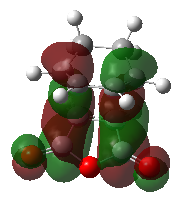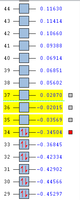Antisymmetric	Antisymmetric

IRC method

File:EndoTS IRC.log

The energy pathway clearly shows that the IRC has been calculated from reactants (high E) to products (low E). The only peak shown corresponds to the Transition state. The Energy converged after 101 steps. The energy of the reactants (first step) was found to be -0.09424406 a.u. and the energy of the product (last step) was -0.16016993 a.u.

Energy along IRC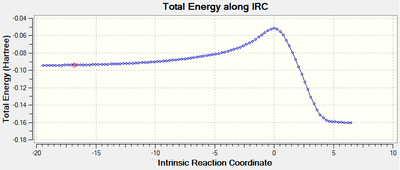
Gradient along IRC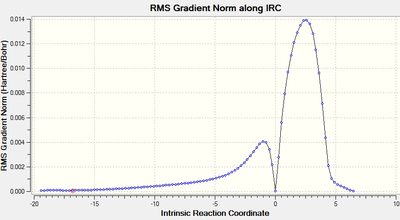
Reaction Pathway	Please click to play

The exo product

The QST2 method

File:Exo qst2.log

The QST2 method was used to find the exo Transition State by labelling the reactant and product molecule as shown below and performing a semi-empirical/AM1 optimisation. The obtained bond distances as well as the energy can be found in the tables below. The frequency analysis indicates that the transition state has been found. Overall the distances are shorter than for the endo transition structure indicating that this system must be more strained than the endo TS. Again the interfragmentary distance C16-C13 lays in between a CC bond length and the sum of the Van der Waals radii. All other bond distances lay in between the sp3-hybridised CC bond length (154 pm) and the sp²-hybridised CC bond length (134 pm).

Reactants	Product

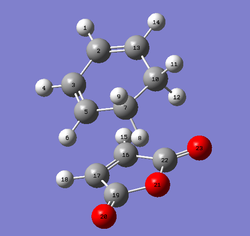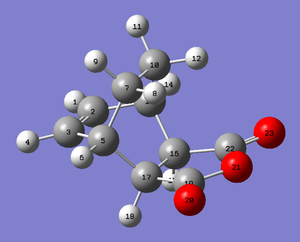Bond	C10-C7	C17-C16	C16-C13	C2-C3	C7-C10
Bond length/Å	1.52207	1.41012	2.17043	1.39674	1.52207

Vibrations	-812.32 cm-1	60.86 cm-1	Energy/Hartrees
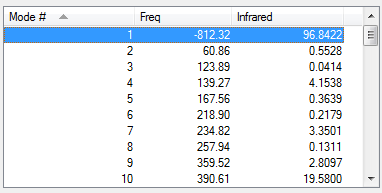Figure 14: Vibrations of the exo Transition State			-0.05041977 a.u.

MO Analysis

The HOMO and the LUMO were plotted for the Exo product. In this transition state the CC double bond п orbitals and the CO п* orbitals do not overlap at all. No secondary orbital interactions were observed. This is consistent with what literature predicts and can be shown by the higher energy of the transition structure. The key difference between the exo and the endo TS is the lack of secondary orbital interactions for the exo product, which is why the Aldo endo-rule usually applies, meaning that the formation of the endo product is preferred due to its lower TS (see Activation energies section below). Regarding the symmetry, both the HOMO and the LUMO are antisymmetric with respect to the reflection plane. The more nodal planes, the higher the energy of the orbital. This is worth knowing, because the LUMO is also antisymmetric with respect to a plane (orthogonal to the reflection plane) between the two fragments.

Table. HOMO & LUMO of the Exo product

HOMO	LUMO	Orbital Energies
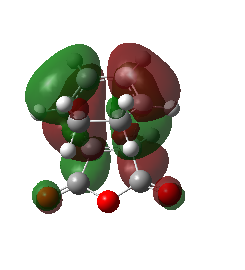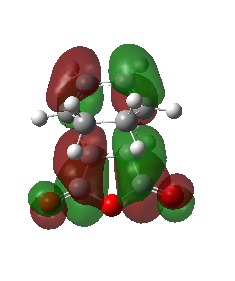Antisymmetric	Antisymmetric

IRC method

File:IRC exo jas.log

The IRC method has been applied (semi-empirical/AM1). The energy converged after 92 steps. The maximum energy where the gradient is equal to zero indicates must represent the transition state. The reaction as shown on the plots is the reverse direction, starting at low energy (from the products) and finishing at high energies (the reactant) along the IRC. The energy of the reactants was -0.09537173 a.u. and the energy of the product was -0.15990908 a.u.

The Gradient along IRC plot clearly shows that when starting at the transition structure (zero gradient) the reaction could either go back to reactants or lead to the product. As mentioned before. The Transition state always follows the reaction path with the steepest slope across the PES, thus the product is formed.

Energy along IRC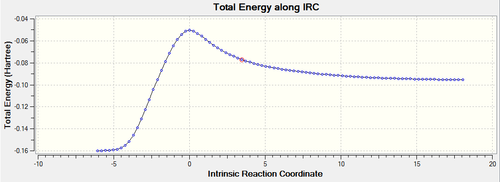
Gradient along IRC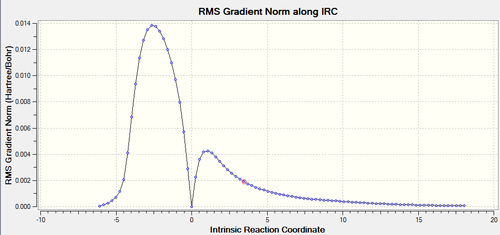
Reaction Pathway	Please expand for IRC animation

Calculating and Comparing the Activation Energies

The necessary information to produce the table below has been obtained from the Thermochemistry section of the corresponding log files. The log files of the two reactants, maleic anhydride and cyplopentadiene, were used, assuming that they approach each other from an initial infinite distance apart. The energies of the two reactants were added together based on the fact that this approach is used in the total Energy along the IRC plot too.

The endo transition structure has the longer bond distance and lower activation energies, indicating that it forms the kinetic product. The secondary orbital stabilisation is so large that it overcomes the increase in steric repulsion, lowering the overall energy of the TS. The exo transition structure is more strained due to its shorter bond distances (interfragmentary distance!) which causes an increase in steric hindrance between the cyclopentadiene part and the anhydride. Thus the exo TS has a higher activation energy. The interfragmentary distance is shorter for the exo TS than for the endo TS, however both lay in the region between normal C-C bond length and the sum of their VdW radii (3.4 Å)

(The sterics actually are worse in the exo TS than the endo Tam10 (talk) 15:59, 24 February 2016 (UTC))

In the calculations of the Diels Alder Transition states, the Frontier Orbital approximation has been neglected. According to this approximation, if the HOMO-LUMO energy gap decreases, the two reactant molecules do not need to come as close together to react. Furthermore, throughout these calculations only the formation of a single DA adduct was studied. Due to this complete isolation intermolecular interactions in solution have been ignored. Moreover, every computational method relies on a number of approximation to work, which may or may not cause a deviation from reality.

	Electronic Energy/Hartrees	Sum of electronic and zero-point energies/Hartrees (at 0K)	Sum of electronic and thermal energies/Hartrees (at 298.15K)
Endo TS	-0.05150436	0.133495	0.143684
Exo TS	-0.05041977	0.134881	0.144881
Cyclohexadiene	0.02771129	0.152501	0.157726
Maleic anhydride	-0.12182422	-0.063345	-0.058191
Reactants	-0.09411293	0.089156	0.099535
ΔE Endo TS	0.04260857	0.044339	0.044149
ΔE Exo TS	0.04369316	0.045725	0.045346

*1 hartree = 627.509 kcal/mol

	Electronic Energy/kcalmol-1	Sum of electronic and zero-point energies/kcalmol-1	Sum of electronic and thermal energies/kcalmol-1
ΔE Endo TS	26.73	27.8231	27.7039
ΔE Exo TS	27.41	28.6928	28.4550

Conclusions

Comparison of Computational Methods

The first section of this experiment - the Cope rearrangement - compared the geometries of the chair and the boat transition structures, as well as the different methods to obtain and optimise them: HF/3-21 vs. B3LYP/6-31Gd. The TS geometry is expected to fail in HF theory if the structure in question has many partial bonds causing large correlation effects, which HF does not account for. However, for many organic reactions HF TS structures were generally of good quality.^[5] The HF geometries obtained throughout were of good quality, only the energies lacked in accuracy.

Density functional theory proved to be an accurate method for calculating geometries and energies. Hence, the calculations of the activation energies confirmed that the Density Functional Theory results agree with experimental results (Chair and Boat Activation energies). Additionally, density functional theory (B3LYP/6-31Gd) allows us to predict the regioselectivity of the Diels Alder Cycloadduct (lower energy transition state). If the two fragments were not symmetrical, the stereoselectivity of the Cycloaddition could have been predicted using density functional theory.^[8]

Semi-empirical AM1 method was used throughout the second section of this experiment.

Endo and Exo Transition Structure analysis

The Alder Endo-rule was confirmed, proving that the endo-product has the lower activation energy, due to the secondary orbital interaction. For both transition structures (exo and endo), the interfragmentary distance was found to lay in between a normal sp³-hybridised CC bond distance and the sum of the Van der Waals radii, indicating some sort of interaction between the two fragments.

It has been confirmed that Secondary interaction among occupied diene and dienophile molecular orbitals only contributes in a minor way to the total energy, because these interactions increase the energy of some levels while decreasing the energy of others. The significant secondary interaction results from the symmetry-allowed mixing between the unoccupied with occupied orbitals, leading to bonding and lowering in energy. In case of the studied [4+2] concerted cycloaddition reaction, the endo transition state is stabilised compared to the exo alternative due to the secondary orbital interactions.Furthermore, Diels Alder reactions which proceed quite readily have an early transition state and an increased reactivity due to a small HOMO LUMO gap, causing a very large splitting. This means, the reactants do not need to approach to such a great extent to react. ^[9]

Limitations

Throughout this Computational experiment, all the methods used have underlying approximations which can falsify the results. As an example, the semi-empirical AM1 method has been formulated based on the Neglect of Differential Diatomic Overlap (NDDO).^[12] Of course many attempts have been made to justify this approximation, saying that it only neglects unimportant integrals eg. Loewdin.[13]

In case of the Hartree-Fock method, the Born-Oppenheimer approximation is always assumed as well as the mean field approximation, which has been mentioned previously. The mean field approximation causes correlation effects to be completely ignored.

When trying to understand and compute the factors affecting chemical reactivity by using the Frontier Orbital approach, there are several factors that cannot be taken into account or they are underestimated. One of these factors might be solvent effect, leading to deviations from experimental values by increasing or decreasing the activation energy. Another factor is the strain of the σ-framework, whether gained or lost, it is never directly included, only indirectly via the energies of the orbitals affected. Similarly, steric effects are not included.^[11]

Further Research

It would be interesting to improve the computational cost as well as the output by develping a new method which would be based on a mix of HF with DFT. HF would supply the computational efficiency whereas DFT could provide the necessary predictive power. Additionally, the deviations from reality due to the neglect of electron correlation.^[14]

(B3LYP incorporates HF into its calculations. Do you mean splitting methods within the same calculation (ONIOM)? Tam10 (talk) 16:03, 24 February 2016 (UTC))

Additionally, only the regioselectivity of the Diels Alder cycloaddition has been studied here. The regioselectivity observed when two non-symmetric (electron donating effect on diene, electron withdrawing effect on dienophile) reactant molecules come together and form predominantly the ortho or the para product, has not been studied here. Furthermore, the stereoselectivity of the Diels Alder cycloaddition could be computed and compared with reality. There was already research done in this field, proving that it is possible to predict the stereoselectivity as well, however

References

[1] D. A. Hrovat, Morokuma et al, J. Am. Chem. SOC.1994,116, 1072-1076

[2] http://www.chm.davidson.edu/ronutt/che401/HartreeFock/HartreeFock.htm, (accessedː10/02/16)

[3] Hammes-Schiffer, Andersen, J. Chem. Ph.1993, 99,

[4] http://www.phys.ubbcluj.ro/~vchis/cursuri/cspm/correlation.pdf, (accessedː 10/02/16)

[5] University of Wyoming, Jan Kubelka, Molecular Modelling Notes, 20

[6] http://scienide2.uwaterloo.ca/~nooijen/Chem-440-computational/Lab_Gaussian_transition_states.pdf (accessedː 11/02/16)

[7] http://www.gaussian.com/g_whitepap/qst2.htm (accessedː 11/02/16)

[8] Kamyar Afarinkia,* Michael J. Bearpark et al, J. Org. Chem, Vol. 68, No. 19, 2003

[9] Roald Hoffmann, R. B. Woodward, J. Am. Chem. Soc., 1965, 87 (19), pp 4389–4390

[10] Michael J. S. Dewar, J. Am. Chem. SOC. 1985, 107, 3902-3909

[11] Ian Fleming, 'Frontier Orbitals and Organic Chemical Reactions', Wiley & Sons Ltd, 1976

[12] http://www.cup.uni-muenchen.de/ch/compchem/energy/semi1.html (accessed: 11/02/14)

[16] M. Bearpark, Calculating Molecular Geometries, QM3 3rd Year

[13] Neymeyr et al, International journal of Quantum Chemistry, Vol. 53, 519-535, 1995

[14] A. D. Becke, J. Chern. Phys. 98 (2), 15 January 1993,

[15] http://www.chemtube3d.com/DAendo_vs_exo,cyclopentadiene_and_maleic_anhydride.html (accessed 12/02/16)