Rep:Mod:Janie192
Computational analysis of cope rearrangement of 1,5-hexadiene
Introduction
The cope rearrangement is an example of a [3,3] sigmatropic pericyclic reaction involving 1,5-hexadiene. The cope rearrangement is a 4n+2 electron system, where the reaction is thermally allowed. The reaction occurs via a Huckel topology with suprafacial components.

There are various possible anti and gauge conformers of 1,5-hexadiene that can be involved in the cope rearrangement. As well as this, there are two possible transition states that can be involved in the reaction mechanism:chair and boat.
Conformational analysis can be a very useful tool to determine which conformers of 1,5-hexadiene make up the reactants, products and transition state of the reaction profile.Conformational analysis calculations can be run on gaussian or on the High Performace Computing (HPC) service and analysis of the calculations are performed on gaussview.
In order to propose a mechanism for the cope rearrangement of 1,5-hexadiene, optimisation calculations are fundamental to determine the most stable conformers of hexadiene. Optimisation calculations are also used to determine which transition state is most stable. By obtaining such information, the minimum energy pathway of the cope rearrangement reaction can be determined. Frequency calculations are used to provide evidence that an optimised structure is at its minimium energy and hence is a stable structure. It can also be used to analyse the vibrational modes of the structure, specifically those whih conform to the reaction mechanism. By computing the energies of the reactant and transition state, the activation energy can be calculated and compared to experimental values. By using different basis sets (e.g 3-21G, 6-31G*) the activation energies can be contrasted with the experimental results. This enables a conclusion to be drawn to which basis set is the most reliable.
The information below gives a detailed account of how computational analysis is used to obtain the useful information obtained above to understand the reaction mechanism of the cope rearrangement of 1,5-hexadiene.
Optimisation of 1,5 anti-hexadiene
A molecule of 1,5-hexadiene is created on gaussview with an anti-periplanar rearrangement about the central four carbon atoms. Prior to optimisation, the molecule is cleaned using the clean tool under edit. The molecule is then optimised using a HF/3-21G method. On gaussian calculation setup, optimisation is selected as the job type and Hartree fock as the method and 3-21G as the basis set. Under the link 0 tab, 250MB is selected as the %memory.
Here is a link to the optimisation calculations published on D-Space DOI:10042/22946 .
The following input file shows that the optimisation calculation was successful since the submitted job converged
Item Value Threshold Converged? Maximum Force 0.000060 0.000450 YES RMS Force 0.000010 0.000300 YES Maximum Displacement 0.000507 0.001800 YES RMS Displacement 0.000171 0.001200 YES Predicted change in Energy=-2.037278D-08 Optimization completed. -- Stationary point found.

The energy of the optimisated anti-hexadiene is -231.69253528au with Ci point group. The Ci point group has two symmetric operations: E-the identity operation and i- inversion through the center of symmetry.
Based on Appendix 1, this optimised structure is identical to the anti 2 optimised structure which has a relative energy of 0.08 Kcal/mol [1]
Optimisation of 1,5 gauge-Hexadiene
A molecule of 1,5-hexadiene with a gauge rearrangement about the central four carbon atoms is created on gaussview. Using the same steps stated above, the molecule is optimised and its energy and symmetry determined.
Here is a link to the optimisation calculations published on D-Space DOI:10042/22949
The following input file shows that the optimised job was successful since the calculations converged
Item Value Threshold Converged? Maximum Force 0.000044 0.000450 YES RMS Force 0.000009 0.000300 YES Maximum Displacement 0.001317 0.001800 YES RMS Displacement 0.000491 0.001200 YES Predicted change in Energy=-3.609692D-08 Optimization completed. -- Stationary point found.
The energy of optimised gauge-hexadiene is -231.69266120au, with a C1 point group ( thus there is no symmetry)

Based on Appendix 1, this optimised structure is identical to the gauge 3 optimised structure which has a relative energy of 0.00 Kcal/mol[1]
The optimisation results show that the gauge conformation is slightly more stable than the anti conformation. This is a consequence of favourable van der waals interactions between the terminal alkene hydrogen atoms in the gauge conformation.Such interactions are stronger in the gauge conformation since the dihedral angle is smaller compared the anti conformer. As a consequence the terminal hydrogen atoms are closer together be enabling stronger van der waals interactions to take place.
Based on these optimsisation calculations, it can be assumed that the most stable structure of 1,5-hexadiene adopts a gauge conformation.Based on appendix 1 the most stable conformer is gauge 3 which has a relative energy of 0.00 Kcal/mol. This conformer has already been located.
Optimisation of anti2 1,5-Hexadiene
Anti2 1,5 Hexadiene with a 3-21G basis set was already optimised and was shown to have a energy of -231.69253528au with Ci symmetry. This has the same energy as anti2 in appendix 1 at -231.69254 au when rounded to 5.dp
Using a larger basis set such as 6-31G* basis set optimisation of anti2 1,5-hexadiene was re-calculated.Here is a link to the DOI for the optimisation calculations published on D-space DOI:10042/23007 . The energy was calculated to be much higher at -234.61170280 au compared to 3-21G. There is a distinct difference in the energies between the two basis sets, however there is very little difference in the geometry. For example the center C-C-C single bond and the terminal C=C-C bond angle is 112.672 degrees and 125.287 degrees respectively for the B3LYP/6-31G* basis set and 111.349 degrees and 124.806 degrees repsectively for the HF/3-21G basis set.
Frequency Analysis of Anti2 1,5-Hexadiene with a 6-31G* basis set
Calculation of the frequency of 1,5-hexadiene is essential to ensure that the optimised structures obtained are at a minimum energy and hence are stable structures. This can be confirmed if all the vibrational frequencies are real and positive and the low frequencies are close to zero.
Using the B3LYP/6-31G* basis set,frequency analysis is carried out by going to Guassian Calculation Setup Frequency is selected as the job type,. It is essential to ensure that the method is still correctly specified as DFT - B3LYP and 631G(d) for the basis set. Under the Link 0 tab change the name of the chk file to the name of the calculation being run i.e frequency calculation.
Here is a link to the frequency calculations published on D-Space: DOI:10042/22955 . The log file is opened to view the vibrational frequencies.
The results of the low frequencies are shown below:
Full mass-weighted force constant matrix:
Low frequencies --- -18.6345 -11.7126 -0.0005 0.0004 0.0007 1.8423 Low frequencies --- 72.7326 80.1452 120.0243
The six low frequencies represent the '6' part of the 3N-6 vibrational energy formula for non-linear molecules. The 6 low frequencies are all very close to zero and the highest low frequency at 1.8423cm-1 is relatively smaller than the lowest real frequency at 72.7326cm-1. Since the low frequencies are close to zero, this proves that the optimised 1,5-hexadiene is at a minimum energy.
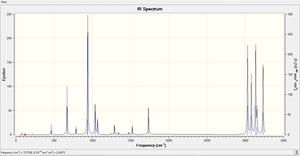
The table below provides a tabulation of the real vibration frequencies and intensities of 1,5-hexadiene. The results show that all the frequencies are positive and are therefore real frequencies. This also gives evidence that a minimum energy has been located for hexadiene
| Mode | Frequency(cm-1) | infrared | Mode | Frequency(cm-1) | infrared |
|---|---|---|---|---|---|
| 1 | 73 | 0 | 22 | 1289 | 6 |
| 2 | 80 | 0 | 23 | 1323 | 0 |
| 3 | 120 | 0 | 24 | 1339 | 0 |
| 4 | 220 | 0 | 25 | 1343 | 1 |
| 5 | 349 | 0 | 26 | 1384 | 0 |
| 6 | 394 | 0 | 27 | 1474 | 0 |
| 7 | 462 | 3 | 28 | 1476 | 2 |
| 8 | 626 | 0 | 29 | 1509 | 0 |
| 9 | 669 | 20 | 30 | 1523 | 6 |
| 10 | 788 | 4 | 31 | 1731 | 0 |
| 11 | 938 | 9 | 32 | 1734 | 18 |
| 12 | 939 | 0 | 33 | 3022 | 0 |
| 13 | 940 | 65 | 34 | 3032 | 54 |
| 14 | 942 | 0 | 35 | 3060 | 0 |
| 15 | 1002 | 0 | 36 | 3080 | 36 |
| 16 | 1034 | 0 | 37 | 3136 | 56 |
| 17 | 1036 | 20 | 38 | 3137 | 56 |
| 18 | 1043 | 0 | 39 | 3155 | 15 |
| 19 | 1068 | 10 | 40 | 3156 | 0 |
| 20 | 1203 | 0 | 41 | 3234 | 0 |
| 21 | 1251 | 1 | 42 | 3234 | 45 |
The corresponding IR spectrum to the vibrational frequencies of 1,5-Hexadiene is shown below
Thermochemistry Analysis of 6-31G basis set
The sum of electronic and zero-point Energies at 0K is -234.469212 au. This term includes the zero-point vibrational energy
The sum of electronic and thermal Energies at 298.15K and 1atm is -234.461856 au. This term includes contributions from translational, rotational, and vibrational energy modes
The sum of electronic and thermal Enthalpies is -234.460912 au. This term contains an additional correction for RT (H = E + RT)
The sum of electronic and thermal Free Energies is -234.500821au. This term contains entropic contribution to the free energy (G = H - TS)
Frequency Analysis of Anti2 1,5-Hexadiene with a 3-21G basis set
Frequency analysis of the lower basis set, 3-21G is also carried out. Here is link to DOI for the frequency analysis calculations published on D-space: DOI:10042/23008
Here is a summary of the low frequencies:
Full mass-weighted force constant matrix: Low frequencies --- -5.6621 -2.3491 -2.0809 -0.0008 -0.0005 0.0005 Low frequencies --- 71.1986 85.6862 116.1461
There is evidence that the optimised structure of 1,5-hexadiene with a 3-21G basis set is at a minimum since its low frequencies are close to zero.
A summary of the vibrational frequencies are shown below. They are all positive and real
| Mode | Frequency(cm-1) | infrared | Mode | Frequency(cm-1) | infrared |
|---|---|---|---|---|---|
| 1 | 71 | 0 | 22 | 1430 | 6 |
| 2 | 86 | 0 | 23 | 1444 | 0 |
| 3 | 116 | 0 | 24 | 1470 | 1 |
| 4 | 249 | 0 | 25 | 1471 | 0 |
| 5 | 377 | 0 | 26 | 1498 | 0 |
| 6 | 445 | 0 | 27 | 1614 | 0 |
| 7 | 506 | 3 | 28 | 1617 | 3 |
| 8 | 682 | 0 | 29 | 1647 | 0 |
| 9 | 745 | 33 | 30 | 1656 | 13 |
| 10 | 855 | 5 | 31 | 1856 | 0 |
| 11 | 975 | 0 | 32 | 1858 | 17 |
| 12 | 1028 | 0 | 33 | 3199 | 0 |
| 13 | 1051 | 0 | 34 | 3206 | 48 |
| 14 | 1095 | 0 | 35 | 3229 | 0 |
| 15 | 1112 | 153 | 36 | 3253 | 24 |
| 16 | 1114 | 0 | 37 | 3303 | 0 |
| 17 | 1160 | 2 | 38 | 3304 | 41 |
| 18 | 1175 | 0 | 39 | 3316 | 12 |
| 19 | 1177 | 10 | 40 | 3316 | 0 |
| 20 | 1306 | 0 | 41 | 3385 | 0 |
| 21 | 1377 | 2 | 42 | 3385 | 45 |
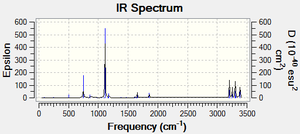
Thermochemistry Analysis of 3-21G basis set
The sum of electronic and zero-point Energies at 0K is -231.539539 au
The sum of electronic and thermal Energies at 298.15K and 1atm is -231.532565 au
The sum of electronic and thermal Enthalpies is -231.531621 au
The sum of electronic and thermal Free Energies is -231.570916 au
Optimizing the Chair and Boat Transition Structures
There are two possible transition state structures for the cope rearrangement of 1,5-Hexadiene, Chair and Boat:

GaussView can be used to optimise the boat and chair TS structures, to visualise the instrinsic reaction coordinate and to calculate the activation energies of the transition state structures by comparing the energies of the transition states with the reactants
The transition states for boat and chair conformations consists of two allyl (C3H5) fragments. Based from this knowledge, optimisation calculations for chair and boat conformers can be developed using optimised allyl fragments
Optimising the Chair transition state
Firstly, an allyl fragment is created in gaussview. The molecule is then optimised using a HF method and a 3-21G basis set.A new window is then created on gaussview, by going to file--> New---> Create new molecule group. Two copies of the optimised allyl fragment group is pasted onto the new molecule window.The fragments are then orientated to the chair transition state conformation at a approximately 2.2Angstroms apart

There are two possible methods that can be used to optimise the transition state:transition state optimisation and the frozen coordinate method
Transition State Optimisation: For transition state optimisations to be successful, the structure of the guessed chair transition state must be reasonable. Transition State optimisation calculations are based on curvature of the reaction coordinate and so if the guessed transition state is far off the reaction coordinate, the optimisation calculation will not be successful. An optimisation calculation for the guessed transition state conformation is run by using the following steps: A copy of the guessed chair transition state is pasted into a new molecule window.Then in gaussian calculation setup Opt +Freq is selected as the job type,optimization to a TS (Berry) is also selected as well as, calculate the force constant once. The phrase, Opt=NoEigen is added to the additional keyword box at the bottom.Hartree Fock is used as the method and 3-21G as the basis set. It's necessary to add the phrase Opt=NoEigen as this prevents the optimisation calculation from failing if more than one imaginary frequency is found, which is often the case when the guessed transition structure is inaccurate.
The optimised structure was shown to have to symmetry with a C2h point group
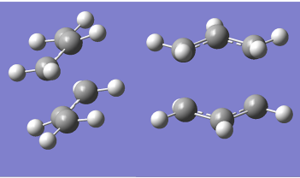
A summary of the vibrational frequencies from the Opt+Freq calculation is shown in the screen shot below.Note there is only one imaginary frequency at ~ 818cm-1)
The distance between the terminal carbon atoms from the allyl fragments is about 2.2 Angstroms

An animation for the imaginary vibrational mode is shown below. This corresponds to the [3,3] sigmatropic cope rearrangement:
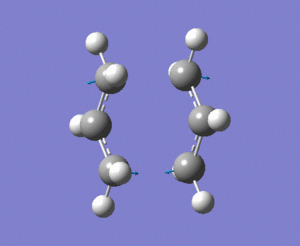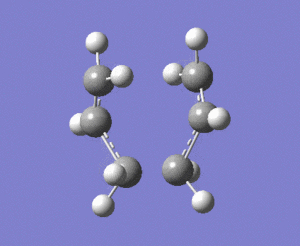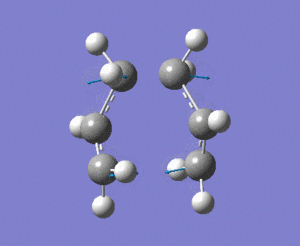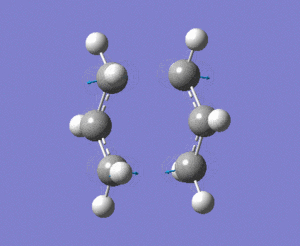
Procedure to carry out Frozen Coordinate Method: The guess structure of the chair TS is copied into a new molecule window. Under the edit menu. redundant Coordinate editor is selected. The 'create a new coordinate' tab is selected at the top left hand corner of the window. Two terminal allyl carbon atoms are then selected(one from each allyl fragment). Bond is then selected instead of unidentified and freeze coordinate instead of add. The 'create a new coordinate' tab is selected again and the opposite terminal allyl carbon atoms are selected. Bond and unidentified is then selected. The distance between the allyl fragments are fixed at 2.2 Å by using the modifying bond tool. An optimisation calculation to a minimum is then run. The check file of the optimised job this then opened. The distance between the terminal carbons is then optimised. In the redundant coordinate editor, a new coordinate is created. Two terminal carbon atoms, that was previously selected is selected again. bond is selected instead of unidentified and derivative instead of add. The same steps are followed for the other bond. A minimum optimisation calculation is then set up with the force constants not being calculated. The job is then submitted.
In my case, the submitted job incurred an error.To resolve this, the input file is opened in word pad. The following phrase was then added to the top hash line: # opt=(ts,noeigen,cartesian) freq rhf/3-21g geom=connectivity. The job was submitted and the optimisation calculation was successful
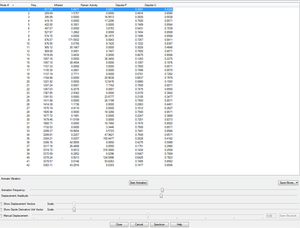
Optimisation calculation of the chair transition structure is repeated using the B3LYP/6-31G* basis set. Results of the calculation are in the results summary below. Here is a link to the DOI DOI:10042/23009
Optimising the boat transition state
Optimisation of the boat transition state is achieved using the QST2 Method. This method involves specifying the reactants and products based on a numbering system for both the carbon and hydrogen atoms in the molecule.The cope rearrangment of hexadiene can be visualised by knowing where the bonds are made and broken. Using a numbering system helps to achieve this.
Initally, the chk file for optimised anti2 hexadiene is opened. Two copies of the optimised structure is made. The images can be viewed side by side, by selecting fit from the downward arrow tab at the top of the window. The carbon and hydrogen atoms are then labelled with numbers by selecting edit and then label. The numbering system of the product hexadiene is then modified based on a numbering system where a the central C-C bond is broken and a new C-C bond is made between the terminal carbon atoms.(see sreenshot image below for the numbering system). A TS(QST2) opt+freq calculation is then made. The job fails since the structure of the product and reactant are far off the boat Transition structure. Thus, for the optimisation calculation to be successful,the geometry of the reactant and product are modified so that they resemble the transition structure more. The C2-C3-C4-C5 dihedral angle is reduced to 0 degrees and the C2-C3-C4 and C5-C4-C3 dihedral angle is reduced to 100 degrees for both the reactant and product structures.

The opt+Freq calculation is sumbitted again. In this case, the optimisation converged. Here is a link to the DOI to the optimisation calculations DOI:10042/23017 The evidence for this is shown in the input file below:
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000018 0.001800 YES RMS Displacement 0.000007 0.001200 YES Predicted change in Energy=-6.691554D-11 Optimization completed. -- Stationary point found. GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
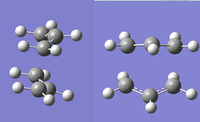
The screen shot below gives a summary of the vibrational frequencies. There is only one imaginary vibrational frequency at -440cm-1, which corresponds to the cope rearrangement

The optimisation calculation for the boat transition structure is repeated using the B3LYP/3-21G* basis set.Results of the calculation are in the results summary below. Here is a link to the DOI DOI:10042/23017
Computation of the minimium pathway of the cope rearrangement to the product
The optimised chair transition structure can be used to determine the minimum pathway of the reaction to the final product. This is known as the instrinsic coordinate method (IRC).
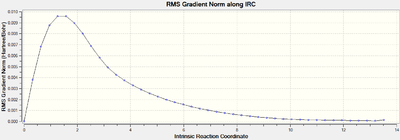
An instrinsic coordinate calculation is run by selecting IRC as the job type. The reaction is computed in the foward direction in order for the optimised structure of the product to be determined. The force constant is computed always and 50 is selected as the number of points computed along the IRC. After the calculation has been completed, the chk point file is opened. The image below, illustrates the RMS gradient transition during the IRC calculation. The last point on the graph has a RMS gradiebnt norm 0.00015225. This value is very close to zero and this shows that the reaction has almost reached its minimum geometry.The structure of the last point on the graph is optimised to a minimum. This results in the 1,5-hexadiene product with a gauge conformation. The energy is -231.69166702 au with C2 symmetry. This corresponds to the gauge2 conformer in appendix 1.

Results Summary
The table below summaries the results for the optimisation and frequency calculations of anti2 hexdiene, chair and boat transition structures for the HF/3-21G and B3LYP/6-31G* basis set. In all three cases, the geometries are very similar between the basis sets, however there is a greater energy difference between the basis sets. The 6-31G* basis set results in higher energy optimisations compared to the 3-21G basis set
| HF/3-21G | B3LYP/6-31G* | |||||
|---|---|---|---|---|---|---|
| Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | |
| at 0 K | at 298.15 K | at 0 K | at 298.15 K | |||
| Chair TS | -231.61932244 | -231.466700 | -231.461340 | -234.55698303 | -234.414929 | -234.409008 |
| Boat TS | -231.60280200 | -231.450928 | -231.444355 | -234.54309307 | -234.402342 | -234.396008 |
| Reactant (anti2) | -231.69253528 | -231.539539 | -231.532565 | -234.61170280 | -234.469212 | -234.461856 |
- 1 hartree = 1 atomic units = 627.509 kcal/mol
Summary of activation energies (in kcal/mol)
The table below provides a summary of the activation energies of the chair and boat structures using the both HF/3-21G and B3LYP/6-31G* basis set. The activation energies were determined by calculating the energy difference between the TS and the anti2 hexadiene.The results at 0k can be compared with the experimental results at 0K. The activation energies calculated for the B3LYP/6-31G* basis set is shown be in closer agreement more with the experimental results compared to the lower basis set. As a consequence it can be concluded that at using the larger basis set, provides more reliable results.
By comparing the activation energies of the boat and chair transition states, for either basis set, it's evident that there is a lower activation energy corresponding to the chair transition state. Thus it can be concluded that the chair transition state is more stable than the boat transition state. The cope rearrangement occurs via the lowest energy pathway i.e, via the chair transition state
| HF/3-21G | HF/3-21G | B3LYP/6-31G* | B3LYP/6-31G* | Expt. | |
| at 0 K | at 298.15 K | at 0 K | at 298.15 K | at 0 K | |
| ΔE (Chair) | 45.71 | 44.69 | 34.06 | 33.16 | 33.5 ± 0.5 |
| ΔE (Boat) | 55.60 | 55.35 | 41.96 | 41.33 | 44.7 ± 2.0 |
Computational Analysis of the Diels Alder Cycloaddition
Introduction
The diels alder cycloaddition reaction is an example of a pericyclic reaction. Cylcoaddition reactions involve the concerted formation of two or more sigma bonds between two or more conjugated pi systems. Cycloaddition reactions can be thermally or photochemically allowed depending on the number of pi electrons involved in the reaction. Diels alder cycloaddition reactions tend to involve a 4pi and a 2pi system. This creates a 4n+2 pi system, making the reaction thermally allowed. They involve a diene which is electron rich and a dienophile which is electron poor. This increases the attraction between the reactants making the reaction more favourable.
Computational analysis can be used to understand the transition state structures , specifically what MOs of the reactants are involved in sigma bond formation, and how the geometry, sterics and stabilising interactions influence the energy of the transition states and the diels alder product formed.
Two different diels alder reactions: butadiene and ethylene; 1,5-cyclohexadiene and maleic anhydride will be analysised.
Diels alder reaction of Butadiene and Ethylene.
The diels alder reaction between butadiene and ethylene is one of the simplest cycloaddition reactions. The reaction occurs via concerted bond formation of two sigma bonds resulting in a cyclohexene molecule. What MOs are involved in the transition state? What is the energy and geometry of the Transition state? These questions can be answered using computational analysis

A molecule of cis-butadiene is initially created in guassview. Cis-Butadiene was then optimised using a AM1 semi-empirical method. Here is a link to the DOI for the optimisation calculations: DOI:10042/23018
The energy of optimised cis-butadiene is 0.04879719 au
To ensure that optimised cis-butadiene is at a minimum, a frequency calculation is necessary. Here is a link to the DOI for the frequency calculations: DOI:10042/23019 . The computed 6 low frequencies are all close to zero.
Full mass-weighted force constant matrix: Low frequencies --- -39.4227 -0.2193 -0.1573 -0.1008 -0.0005 0.9975 Low frequencies --- 2.6560 312.4393 485.2257

The summary of vibrational frequencies shows that there is one imaginary frequency at -39cm-1
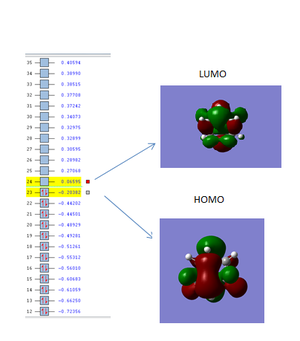
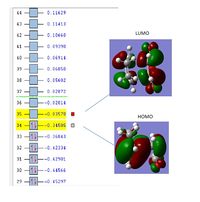
The images of the computed homo and lumo orbitals are shown below:
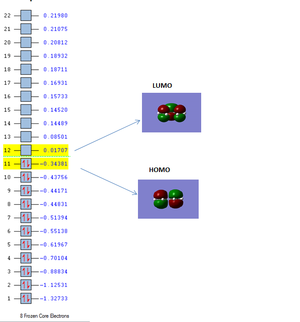
The HOMO orbital is antisymmetric with respect to the plane of the molecule whiles the LUMO orbital is symmetric with respect to the plane of the molecule
A guess structure for the cycloaddition transition state is next created in guassview.A TS(Berry) optimisation calculation is then performed. The force constants sre calculated once and Opt=NoEigen is added to the additionsl keyword box.The optimisation calculation was successful. The image below, illustrates the geometry of the optimised transition state.
The image below shows a plot of the of the HOMO and LUMO orbitals of the transition state. The HOMO and LUMO orbitals are both Antisymmetric
The bond lengths of the partially formed sigma C-C bonds are approximately 1.47 Å. This value is within the range of a typical sp3 bond at 1.54 Å and a typical sp2 bond at 1.33 Å. This highlights the transition of the terminal carbons in both in ethylene and butadiene from being sp2 hybridised to sp3 hybridised carbon during the course of the cycloaddition reaction. The van der waals radius of carbon is 1.70 Å. This means that there there is orbital overlap present between the carbon atoms since the distance between them is shorter than the van der waals radius.
The optimised transition state has an imaginary vibrational frequency of -554cm-1. This corresponds to the concerted bond formation between butadiene and ethylene. The animation below shows that the formation of the two sigma bonds is synchronous. Both butadiene and ethylene bend in the same direction, harmonously. This supports the supposed concerted bond formation mechanism of a diels alder reaction.
Contrastingly, the vibrational mode for the lowest real frequency at 165cm-1 shows that the bond formation is asynchronous. Butadiene and ethylene bend in opposite directions, anharmonously.

The diels alder reaction between butadiene and ethylene is a thermal reaction since it involves a 4n +2 pi system. Thermal systems occur via Hückel topology. For a thermal pericyclic reaction to be allowed, the Woodward-Hoffmann rules states that the total number of (4pi +2)s and (4pi)a components must be odd. In this case there is only one (4pi+2)s component (ethylene) and no (4pi)a components. Hence the total is one and so the reaction is allowed.[2]
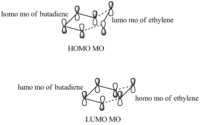
The HOMO MO of butadiene and the LUMO orbital of ethylene have been used to create the HOMO TS. The interaction between these MOs is possible since there is a small energy gap between these MOs which leads to efficient orbital overlap.
Diels-Alder reaction of cyclohexa-1,3-diene with maleic anhydride
In diels alder reaction between maleic anhydride and cyclohexa-1,3-diene there are two possible cycloaddition products: EXO and ENDO. The ENDO product is the kinetic product whiles the EXO product is the thermodynamic product. Only the ENDO product is formed during the cycloaddition reaction.This is due to favourable secondary orbital interactions that take place between the p-orbitals of the carbonyl group on maleic anhydride with the developing pi bond on cyclohexa-1,3-diene. This orbital interaction helps to bring the two reactants together, making the ENDO TS more stable than the EXO TS.
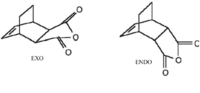
The EXO product is formed due to the formation of both sigma bonds on the bottom face of cyclohexa-1,3-hexadiene (π4s) and the top face of maleic anhydride (π2s).
A guess structure for the transition state of the exo product was created on gauss view. An opt+freq calculation was then run using an AM1 semi-empirical method, optimised to a TS(Berry), the force constants are calculated once and the phrase Opt=NoEigen is added to the additional keyword box.
The energy of the optimised exo transition state was calculated to be -0.05041980 au
The ENDO product is formed due the formation of both sigma bonds on the bottom face of cyclohexa-1,3-diene but on the bottom face of maleic anhydride. Following the same steps used above,the energy of the optimised endo ts was calculated to be -0.05150479 au. Thus the endo ts is lower in energy and hence more stable than the exo ts. This supports the presence of favourable secondary orbital interactions in the endo ts.
Comparison of optimised EXO and ENDO Transition States
From the calculations above, it's has already been established that the endo transition state is more stable than the exo. But what causes the endo to be more stable?
The homo-lumo mo plot illustrates that there are favourable secondary bonding orbital overlap interactions present between the -(C=O)-O-(C=O)- fragment with cyclohexadiene in the HOMO MO endo ts.This bonding interaction is a secondary orbital interaction which doesn't lead to any bond formation but instead induces stabilisation in the transition state. It is only the primary bonding interactions between the pi orbitals of maleic anhydride with the pi orbitals of the 1,3-cyclohexadiene which leads to the formation of two sigma bonds during the reaction. The image of the HOMO endo MO illustrates that the p orbitals on the carbon atoms of the carbonyl group on maleic anhydride are in phase with the p orbitals at the rear end of cyclohexadiene(i.e.there is no node present between the -(C=O)-O-(C=O)- fragment and the C=C-C=C part of the cyclohexadiene molecule).The image below illustrates a simplified diagram of the secondary orbital interactions and the primary bonding interactions in the endo ts. [3]

In the case of the exo transition state there are no secondary orbital interactions present. The -(C=O)-O-(C=O)- fragment is orientated away from the C=C-C=C part of the cyclohexadiene molecule since the two sigma bonds are formed on the top face of maleic anhydride in the exo product. As a consequence there are no additional orbital interactions present; There are only primary orbital interactions between the C=C p-orbitals of maleic anhydride and the terminal p orbitals of the two c=c bonds in cyclohexadiene. This is illustrated in the simplified orbital diagram below


However, there are other factors that must be considered to understand why the endo transition state is more stable than the exo. Steric effects is an important consideration.The through space c-c distances between the CH2-CH2 fragment and the -(C=O)-O-(C=O)- fragment in the exo TS and the CH=CH fragment and the -C=O)-O-(C=O- fragment are approximately equal at 2.9 angstroms. In the endo transition state,-(C=O)-O-(C=O)- fragment are involved in favourable bonding interactions with the CH=CH fragment on the cyclohexadiene. There are no significant steric hinderances between these two fragments. In the exo transition state, steric hinderance is present between the -(C=O)-O-(C=O)- fragment and the CH2-CH2 fragment. There are no secondary orbital interactions in the exo ts to help stabilise the structure and so the exo ts is more stable than the endo. This shows that there is a compromise between favourable secondary orbital interactions and steric repulsion in the molecule.[4]
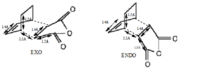
The sketch of the C-C bonds in the ENDO and EXO ts shows that the length of the partially formed C-C sigma bonds is approximately 2.2 Angstroms. This is much longer than a typical C-C bond at 1.47 Angstroms but is shorter than twice the van der waals radius of carbon. This highlights that the c-c bonds are only partially formed.Other C-C bonds present in the transition state are shorter than 2.2 angstroms, where they range from 1.4-1.5 Angstroms.
The endo ts has an imaginary vibrational frequency of -806cm-1 and the exo ts has an imaginary vibrational frequency of -812cm-1. Both correspond to the vibrational mode for concerted bond formation.

Computation of the minimium pathway to the minimum product
From the optimised endo TS, the minimum pathway is computed to determine the endo product. This is achieved by carrying out an IRC calculation. By following the same procedure as that used for the IRC calculations for the cycloaddition reaction between butadiene and ethylene, the last point of the RMS gradient norm graph was computed to be 0.000037631. The structure of the last point was then optimised to a minimum. The energy of the optimised endo product was calculated to be -0.16017082 au.
Similarly, from the optimised exo ts, the minimum pathway can be computed to determine the exo product. The IRC calculation was run and the last point on the graph was computed to have a RMS gradient norm of 0.0000399497. The last point was optimised to a minimum. The energy of the optimised exo product was calculated to be -0.15990937 au.

The results from the IRC calculation show that despite the endo ts being more stable than the exo ts, the exo product is in fact more stable than the endo product as highlighted by the calculated energy differences. The exo product is the thermodynamic product and will be formed in excess only if the reaction is forced into reversible reaction conditions. This usually involves higher temperatures compared to the kinetically controlled reaction. The endo product is only formed since it has a lower energy pathway compared to the exo product. This is a consequence of the secondary orbital interactions present in the transition state which aids stabilisation.