Rep:Mod:JakeHooton Experiment1C

Computational Project for Experiment 1C (Jake Hooton)

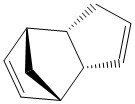
Firstly, the endo- and exo- products of the cyclopentadiene dimerisation reaction, and also the hydrogenation products of the endo- dimer, were optimised in ChemBio 3D, in order to become familiar with the MMFF94 technique, and practise comparing its results. The procedure is documented below:

Exo product:

Molecular Mechanics Energies for Cyclopentadiene Dimer Derivatives

Energy Criterion	1 - Exo Dimer	2 - Endo Dimer	3 - Endo-SixMemHydrogenated	4 - Endo-FiveMemHydrogented
Picture
Total Bond Stretching Energy/ kcal/mol	3.54300	3.46648	2.82311	3.31205
Total Angle Bending Energy/ kcal/mol	30.77271	33.19349	24.68537	31.93564
Total Stretch Bending Energy/ kcal/mol	-2.04139	-2.08194	-1.65719	-2.10249
Total Torsional Energy/ kcal/mol	-2.73103	-2.94935	-0.37838	-1.46988
Total Out-Of-Plane Bending Energy/ kcal/mol	0.01485	0.02209	0.00028	0.01315
Total Van der Waals Energy/ kcal/mol	12.80163	12.35599	10.63728	13.63773
Total Electrostatic Energy/ kcal/mol	13.01367	14.18397	5.14702	5.11948
Total Energy (Sum Of Terms)/ kcal/mol	55.37344	58.19073	41.25749	50.44567

Comparison of the total energies for the exo- and the endo- products of the cyclopentadiene dimerisation shows that the endo product is ~3 kcal/mol higher in energy than the exo product. This tells us that the exo product should be the thermodynamic product of the dimerisation reaction. We know in fact, that there is a greater preference for the endo product to be formed in this reaction, therefore we can conclude that the endo product is the kinetic product of this reaction, and the transition state for forming this product sits at a lower energy than the corresponding exo- transition state. This is indeed rationalised in theory by considering the stabilisation of the the reacting pericyclic pi-system in the endo- transition state, by the other double bond (pi electrons) in the cyclopentadiene molecule which is acting as the dienophile.

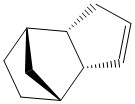
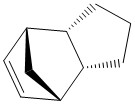
The two hydrogenation products, 3 and 4, each have a lower total energy than their precursor 2, the endo product of the cyclopentadiene dimerisation. This suggests that the hydrogenation products are thermodynamically more stable. This can be rationalised by considering that they are saturated, and more substituted than the alkene precursor 2. Compound 2 is higher in energy due to electrons sitting close together in a pi system, rather than in separate sigma 'bonds' where they are more 'on their own'.

Compound 4 is much higher in energy than compound 3 (the hydrogenated products), this is mainly due to a contribution from the angle bending factor. This can be rationalised due to the fact that the bridging methylene group is in much higher angle strain in compound 4, due to the double bond in the six-membered ring it bridges being shorter than a single bond and contracting the ring, straining the bridgehead. This is not present in compound 3 since the other bond was hydrogenated.

Main differences are in angle bending energy and van der waals energy (Analyse with MM description? Bond length description etc? vdw dispersion good or bad?

Finding the most stable conformation of a precursor to Taxol

Jmol file for taxol precursor with carbonyl down <-- Get rid of this.

Using the programme Avogadro, molecular mechanics optimisations were carried out on different conformations of the following molecule (a precursor to Taxol), using the MMFF94s with the 'conjugate gradients' setting. Initially, two conformations of this molecule were presented, with the carbonyl group pointing either up or down. These were initially drawn in chemdraw, imported in to the Avogadro programme, and the intial guess geometry corrected before the optimisation. - These optimisations are presented in columns 1 and 4 of Table 1. .

It was found that these optimisations converged correctly for the left hand side of the molecule, however they gave a twist-boat conformation for the six-membered ring on the right hand side of the molecule. Twist-boat conformations are only a local minimum for the text-book case of cyclohexane, with the well-known chair conformation satisfying the criteria for a global minimum. Therefore, it was likely that conformers of the taxol precursor with a chair conformation of the ring on the right would be at a lower energy still.

After many failed calculations, with the ring on the right continuing to converge to a twist boat structure, conformers of the molecule were successfully found with a 'chair' ring on the right. This was after much care was taken to define an initial guess geometry with quite accurate positioning for expected axial and equatorial hydrogens around the ring, with respect to the other substituents (namely, two wedge bond 'up' hydrogens and two dash bond 'down' R groups, which comprise the left hand side of the molecule).

The optimisations for the 'chair' conformers of the carbonyl-down and carbonyl-up forms of the molecule are presented in columns 2 and 3 of Table 1, below:

Table 1:

Molecular Mechanics Energies for Taxol Precursor Conformers

Energy Criterion	1 - PreTaxol-CarbonylDown-TwistBoat	2 - PreTaxol-CarbonylDown-Chair	3 - PreTaxol-CarbonylUp-Chair	4 - PreTaxol-CarbonylUp-TwistBoat
Picture	JakeTryAgain	JakeTryAgain	JakeTryAgain	JakeTryAgain
Total Bond Stretching Energy/ kcal/mol	7.75713	7.57636	8.49684	9.13625
Total Angle Bending Energy/ kcal/mol	19.01184	18.82447	33.68489	31.25434
Total Stretch Bending Energy/ kcal/mol	-0.13580	-0.14464	0.08806	-0.16721
Total Torsional Energy/ kcal/mol	3.75902	0.28554	3.28259	7.92220
Total Out-Of-Plane Bending Energy/ kcal/mol	0.9829	0.85179	1.54446	1.93165
Total Van der Waals Energy/ kcal/mol	35.00189	33.20956	35.50610	39.45800
Total Electrostatic Energy/ kcal/mol	-0.05987	-0.04756	0.20117	0.40020
Total Energy (Sum Of Terms)/ kcal/mol	66.29251	60.55552	82.80413	89.93544

Comment/Results: Clearly, the conformers with chair conformations of the ring on the right are lower in energy - by ~6 kcal/mol for the carbonyl-down forms, and by ~7 kcal/mol for the carbonyl-up forms. The main contributing terms between these differences in total energy are again highlighted in lime green - they are the torsional strain and the van der Waals dispersion. (between columns 1 and 2, then 4 and 3, respectively).

For the torsional contribution, both carbonyl-down forms have lower energy than the carbonyl-up forms, and this can be understood by considering

The large contribution of the angle bending and van der Waals terms can be rationalised by considering the data in Table 1.1.

Table 1.1:

For each form, the chair conformer is lower in these terms than the twist-boat by 2 to 4 kcal/mol.

Following this, I realised that there could equally possibly be other conformers, with the six membered-ring sitting in the opposite chair conformation. With similar guess procedures for the first pair of chair conformers (aligning axial and equatorial positions for hydrogens and substituents), the alternative pair of chair conformations for the carbonyl-down and carbonyl-up forms were successfully optimised. The results for these two conformers are presented below in table 2.

Table 2:

Molecular Mechanics Energies for Taxol Precursor Conformers

Energy Criterion	5 - PreTaxol-CarbonylDown-Chair-Other	6 - PreTaxol-CarbonylUp-Chair-Other
Picture	JakeTryAgain	JakeTryAgain
Total Bond Stretching Energy/ kcal/mol	8.64270	7.64629
Total Angle Bending Energy/ kcal/mol	21.80021	28.28091
Total Stretch Bending Energy/ kcal/mol	-0.21793	-0.08132
Total Torsional Energy/ kcal/mol	6.43313	0.29811
Total Out-Of-Plane Bending Energy/ kcal/mol	1.62912	0.97597
Total Van der Waals Energy/ kcal/mol	36.09551	33.11982
Total Electrostatic Energy/ kcal/mol	0.40312	0.30525
Total Energy (Sum Of Terms)/ kcal/mol	74.78587	70.54502

Further Comment/Results: Optimising these each conformes, with the alternative chair conformation of both the carbonyl-up and carbonyl-down forms, has shown that for the carbonyl-up form, the alternative chair is the lowest energy conformer, but for the carbonyl-down form, the alternative chair is a much higher energy conformer. Again, the major factors for the stabilisation or destabilisation in each case, occur in the terms highlighted in lime green - those for angle bending energy, torsional strain and van der Waals dispersion.

These results suggest that there is an inherent relationship between the orientation of the carbonyl group in the left hand side of the the molecule and the chair form in which the right hand side of the molecule will sit.

It can also be seen, having found these six conformers, that the global lowest energy conformer is the carbonyl-down form, first chair conformer - number 2. Another, overall point of note is that there is a very large difference in angle-bending energy, between the carbonyl-up and carbonyl-down forms in each case. This is highlighted in dark green in the tables, and shows that in general the carbonyl-up forms are strongly disfavoured due to bond bond angle strain across the molecule - this will be due to strain away from the normal tetrahedral and trigonal planar bond angles at sp3 and sp2 hybridised carbon atoms, in the larger 'backbone' ring of the molecule, in order to accommodate an 'up' carbonyl.

NMR

The next task was to optimise and run an NMR analysis on a following precursor to the taxol molecule - differing from the previous one in that it had an -SCH₂CH₂S- group attached to a carbon in the 'ring on the right' and a methyl group substituted instead of a hydrogen atom, on one of the fused carbons (joining to the rest of the molecule) in this ring. In order to choose the lowest energy conformer of this molecule to optimise, the input structure was based upon the lowest energy structure of the previous precursor (number 2, with the carbonyl pointing down and the ring on the right sitting in its first chair form, with the carbons closest to us pointing down from the page).

This conformer for the new precursor was constructed in Avogadro, optimised with the MMFF94s method, and submitted to Gaussian for an NMR calculation. When Avogadro was made to export a Gaussian input file for this calculation, keywords were added to re-optimise this structure at the 6-31G(d,p) level, then carry out a Freq + NMR analysis, with chloroform as the solvent and with EmpiricalDispersion=GD3.

The result is available here: DOI:10042/26514 , and the output geometry was also saved as a mol file, then opened with Avogadro and saved as a cml file, so that the resulting geometry may be visualised as a JMOL file within the results table below. A link to a JPEG of the computed spectrum is also included in the table, and a large, labelled picture of the structure is included below the table, to show which carbon within the molecule gives rise to each shift.

caption

Calculated 13C Chemical Shifts / ppm	Experimental 13C Chemical Shifts / ppm {From the literature}	Pictures
213.05	211.49	JakeTryAgain
148.01	148.72
120.22	120.90
93.27	74.61
65.94	60.53
55.04	51.30
55.01	50.94
49.67	45.53
48.11	43.28
45.80	40.82
44.16	38.73	A picture of the calculated 13-C NMR spectrum. Please click through twice to view largest form of image.
41.35	36.78
38.73	35.47
33.72	30.84
32.58	30.00
28.41	25.56
26.51	25.35
24.57	22.21
24.17	21.39
22.58	19.83

As can be seen in the table, for the most part, the calculated and experimental NMR shifts match up well. There is one anomaly, highlighted in lime green, which shows a noticeable discrepancy. This can be attributed to inaccuracies in the method of compuation - the carbon responsible for this shift (computed at 93.27 ppm) has two adjacent sulphur atoms in the molecule, and the presence of larger atoms such as sulphur typically provides inaccuracies in computed NMR shifts due to spin-orbit coupling effects.

Part 2

Molecular Mechanics Energies for C

Energy Criterion	1 trans stilbene trans	2 trans stilbene cis	3 bmstyrene trans	4BM Styrene cis
Picture	JakeTryAgain	JakeTryAgain	JakeTryAgain	JakeTryAgain
Total Bond Stretching Energy/ kcal/mol	3.72863	3.87037	1.88605	1.92512
Total Angle Bending Energy/ kcal/mol	2.69579	3.08977	1.73612	2.17362
Total Stretch Bending Energy/ kcal/mol	-1.54314	-1.41613	-0.76410	-0.70660
Total Torsional Energy/ kcal/mol	2.33100	2.32973	2.89557	2.91439
Total Out-Of-Plane Bending Energy/ kcal/mol	0.00285	0.00587	0.00163	0.00197
Total Van der Waals Energy/ kcal/mol	26.89215	26.75211	14.32349	14.54078
Total Electrostatic Energy/ kcal/mol	5.35094	6.85416	3.04157	3.04019
Total Energy (Sum Of Terms)/ kcal/mol	39.45822	41.48589	23.12034	23.88947

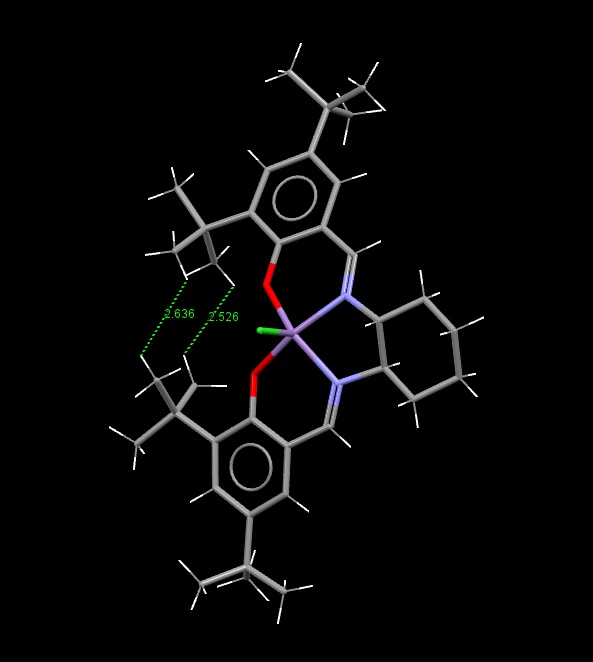
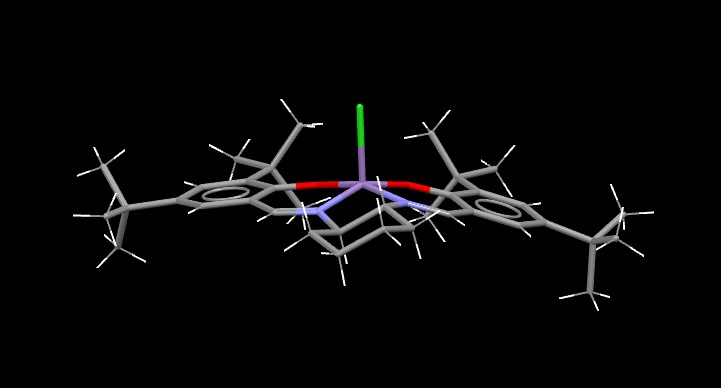
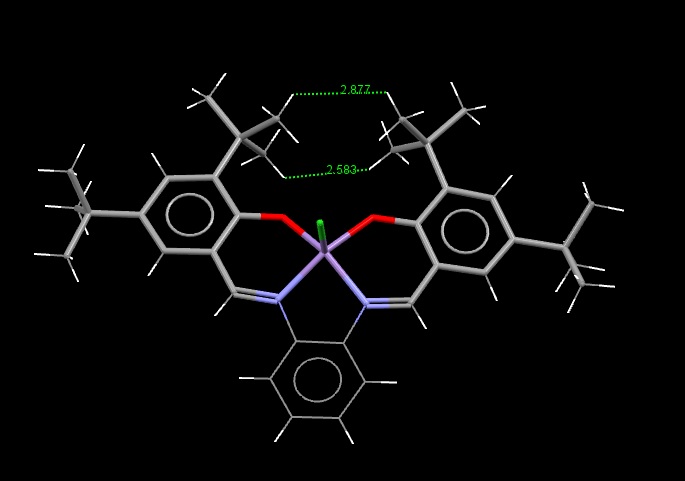
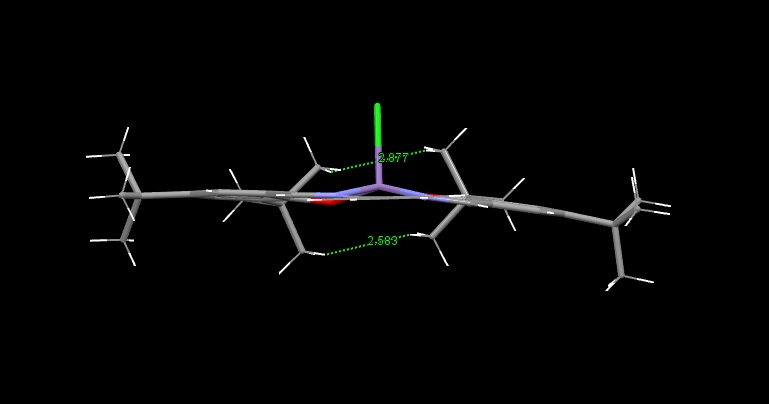
The Structure of the Catalysts

Searches of the Cambridge Crystal Database were carried out by drawing the structures of the desired molecules in the ConQuest programme. The correct structures were obtained, and visualised in the programme Mercury:

Shi Catalyst:

Shi Catalyst

Descriptions

Picture NELQEA

The abbreviation for the Shi catalyst is NELQEA on the database. A prominent anomeric effect is visible in this structure. The anomeric carbon is the one which is a member of both the central six-membered ring and also of the five-membered ring on the right. There is an oxygen atom in the six-membered ring, adjacent to the carbon, and an alkoxy group (part of the five-membered ring on the right), also attached to this carbon. Together these fulfil the criteria for the anomeric effect to be observed. The alkoxy part of the of the five-membered ring is sitting in an axial position on the six-membered ring - this is because it is stabilised by donation in to its C-O sigma* NBO from the axial lone pair of the oxygen in the six membered ring. This stabilising donation is not possible in the equatorial position because overlap with with the equatorial lone pair on the oxygen in the six membered ring is worse. Both C-O bond lenghths about the O-C-O anomeric centre can be seen to be 1.403 Angstroms - in general, significantly shorter than the other corresponding C-C bonds in the rings in the molecule. Other O-C-O centres also exist in the Shi catalyst (the two 'end' carbons that are still members of each five-membered ring), but the anomeric effect is not so prominent here, because the O-C-O units are in five-membered rings and not six-membered rings (hence the NBO overlaps are not aligned so well for the anomeric stabilisation to take place)

Jacobsen Catalyst:

Jacobsen Catalyst

Descriptions	Picture TOVNIB
The abbreviation code for the Jacobsen catalyst is TOVNIB on the database. The two tertiary butyl groups can be seen to have a very close approach, as indicated by the distances highlighted in the diagram. The tertiary butyl groups have orientated themselves so that, mutually, they do not share a particular methyl group clashing head on with one from the other group. Instead, the tertiary butyl groups orientate themselves so that they present two methyl groups facing the opposite tertiary butyl group. In this way, the two pairs of opposing methyl groups are not so close to their counterparts as for the one-on-one case. The internuclear distances for the terminal hydrogens are of the order of 2.7 Angstroms, which is van der Waals attractive rather than repulsive,
It can also be seen that the chair conformation of the ring adjacent to the Mn centre in the Jacobsen Catalyst, forces the rest of the molecule away from a non-planar structure (the remaining part of the catalyst is a conjugated, fused ring structure which would normally prefer to sit planar). In order to confirm this reasoning, another search was performed and the molecule in the following table was compared to this one.

Similar Structure to Jacobsen Catalyst, benzene ring instead of cyclohexane:

Descriptions	Picture RUPWAB
Another molecule, similar to the Jacobsen catalyst and with the abbreviation code RUPWAB, was found by searching with conquest. Instead of a cyclohexane ring adjacent to the Mn centre, this compound has a benzene ring.
The benzene ring is planar, and does not adopt a chair conformation like the cyclohexane ring. As can be seen in the last picture on the right, the benzene ring does not force the rest of the molecule away from being planar, as a result of sitting planar itself. This confirms my earlier reasoning. The RUPWAB molecule does show ever such slight deviations away from a planar structure - this is likely due to the fact that co-ordination around the Mn centre atom would not favour a planar structure with a Cl protruding from only one side, leaving a very open face. Instead, a structure tending slightly towards a square-based pyramid is adopted around this Mn centre instead.

Epoxide Spectra Write Up

Stilbene trans Epoxide DOI:10042/26515

Stilbene cis Epoxide DOI:10042/26516

Beta Methyl Styrene trans EpoxideDOI:10042/26518

Beta Methyl Styrene cis EpoxideDOI:10042/26517

Optical Rotation Calculations

For the trans epoxide of Beta-methyl Styrene:

[Alpha] ( 5890.0 A) =     -102.34 deg.

 [Alpha] ( 3650.0 A) =     -431.73 deg

as found here DOI:10042/26519

For the cis epoxide of Beta-Methyl Styrene

[Alpha] ( 5890.0 A) =     -119.47 deg.

 [Alpha] ( 3650.0 A) =     -424.76 deg

as found here DOI:10042/26533

Transition States Shi Catalyst

Introduction:

Examining the transition states for all the possible reaction pathways in the asymmetric epoxidation of alkenes can be used as a check for the previous enantiomeric assignment of the alkenes (from comparing computed and calculated optical rotations). Using the Shi catalyst, there are four possible transition states for each enantiomer of the alkene in question.

The computed log files for each transition state were obtained below from their DOI addresses, provided for us on the instructions page. Their relative energies are then compared to make the check for the enantiomeric assignments.

The total energy corrected for entropy, zero-point thermal energies and a correction for water solvation was identified in order to compare the transition states. This is identified in the following way (using the first R,R transition state as an example).

The total energy from the results summary for the first R,R transition state is given as -1343.43635979 a.u., but this does not include the corrections. The corrections and the corresponding adjusted total energy can be found from the following text in the log files:

Zero-point correction=                           0.468068 (Hartree/Particle)
 Thermal correction to Energy=                    0.494251
 Thermal correction to Enthalpy=                  0.495195
 Thermal correction to Gibbs Free Energy=         0.413390
 Sum of electronic and zero-point Energies=          -1342.968292
 Sum of electronic and thermal Energies=             -1342.942109
 Sum of electronic and thermal Enthalpies=           -1342.941165
 Sum of electronic and thermal Free Energies=        -1343.022970

Here we are interested in the last of the four corrections (in this case adding 0.413390 a.u.), meaning that the corrected total energy is raised slightly to -1343.022970. The corrected energies for all of the transition states are given in this way in the table below (template with DOIs copied from instructions page):

Transition states for Shi epoxidation of trans-β-methyl styrene

R,R series	R,R energies	S,S Series	S,S energies
DOI:10.6084/m9.figshare.738028	-1343.022970	DOI:10.6084/m9.figshare.738038	-1343.017942
DOI:10.6084/m9.figshare.749615	-1343.019233	DOI:10.6084/m9.figshare.739115	-1343.015603
DOI:10.6084/m9.figshare.738036	-1343.029272	DOI:10.6084/m9.figshare.739116	-1343.023766
DOI:10.6084/m9.figshare.738037	-1343.032443	DOI:10.6084/m9.figshare.739117	-1343.024742

Comment:

For each of the R,R and S,S series, the third and fourth transition states are significantly lower in energy than the first two. By inspecting the animated transition states in the table below, it can be seen that this difference arises from which of the two dioxirane oxygens on the Shi catalyst is used for the transfer during the epoxidation.

The two dioxirane oxygens can each be labelled as either 'up' or 'down' with respect to their orientation towards the oxolane ring which is only joined to the central 6-membered ring by one atom (no attention is paid to the other oxolane ring, which is joined to the central six membered-ring by two atoms. If a dioxirane oxygen is on the same side of the the six membered ring as the two oxygens in the described oxolane ring, it is described as 'up'. If the dioxirane oxygen is on the opposite side of the six membered ring to the two oxygens in the described oxolane ring, then it is labelled 'down'.

For the higher energy (first and second) transition states in each series, it is the 'down' oxygen which is transferred in the epoxidation. For the lower energy (third and fourth) transition states in each series, it is the 'up' oxygen which is transferred in the epoxidation.

Other patterns are also visible, for example the S,S series is always lower in energy than its R,R equivalents. This seems strange at first, since most physical properties (apart from optical rotation) are not altered by enantiomeric configurations. This could be due to natural errors in the computations (the methods are not totally accurate), or perhaps it could be due to the orientations of the catalyst, and one of the reasons for its high enantioselectivity? The reasons are not clear and the selectivity (in my personal case) not entirely understood, so no further discussion is made here.

Equally, the second and third transition states are lower higher in energy than the first and fourth transition states respectively, for each series. This difference is more marked in the R,R series than in the S,S series. The reasons for these trends are harder to rationalise - arguments can be made about which oxolane ring of the catalyst is orientated towards either the phenyl or methyl group of beta-methyl styrene, and whether the phenyl group shows a planar face directly towards two oxygens in an oxolane ring, or just one, due to the orientation of the oxolane ring to the phenyl group. The latter point would lead to considerations of stabilisation of the transition states due to exo/endo phenomena and the lone pairs on either one or two oxygens being in electronic communication with the pi-system in the phenyl group. By looking at these factors in the animated transtion states below, they cannot be linked clearly to described trends - in some cases the phenyl group appears to be nowhere near either oxolane ring on the Shi catalyst! In light of this, no further discussion is made.

Animations of Transtion States

R,R Series	R,R Animation	S,S Series	S,S Animation
R,R 1		S,S 1
R,R 2		S,S 2
R,R 3		S,S 3
R,R 4		S,S 4

The lowest energy (most negative) transition state in the case of each enantiomer (R,R or S,S) is the fourth one. A comparision can be made between the total energies for each of these transition states in order to calculate the enantiomeric excess. The difference (in a.u. or Hartreees) is:

-1343.024742 - -1343.032443 = 0.007701 a.u..

In kilojoules this is: 20.22 kJ mol.

The equilibrium constant, K is equal to K = exp(-ΔG/RT). Using ΔG = 20,220 J/mol, R=8.315 J/(K mol) and T=298 K, this gives K =3499, or an excess of 3499 times more R,R enantiomer than S,S enantiomer.

The percentage excess is then calculated by (3499/3500)*100, giving 99.97% excess of the R,R enantiomer. This compares favourably to the value of 95.5% given in the literature, a very high enantiomeric excess of the R,R enantiomer.

Transition States Jacobsen Catalyst

Introduction:

Energies for each of the possible transition states were found in a similar way to for the Shi Catalyst transition states:

Transition states for Jacobsen epoxidation of trans-β-methyl styrene
S,S series	S,S Energies	R,R Series	R,R Energies
DOI:10042/25945	-3383.262481	DOI:10.6084/m9.figshare.856649	-3383.253816
DOI:10.6084/m9.figshare.856650	-3383.257847	DOI:10.6084/m9.figshare.856651	-3383.254344

Comment:

The differences in (corrected) total energy are much smaller for the Jacobsen catalyst than the differences in total energy for all of the Shi catalyst transition states.

Animations of Transtion States

S,S Series	S,S Animation	R,R Series	R,R Animation
S,S 1		R,R 1
S,S 2		R,R 2

NCI analysis

File:JakeHootonJacobsenSS1NCI.cub.jvxl

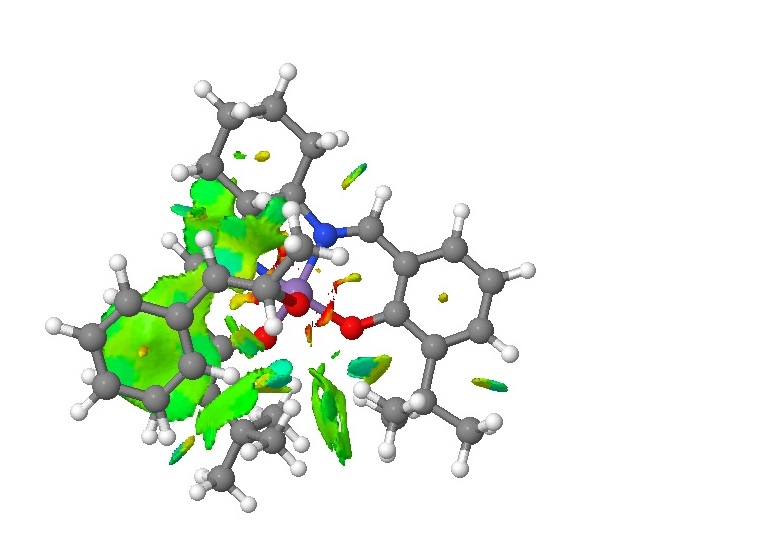
The lowest energy Jacobsen catalyst transition state for beta-methyl styrene(S,S 1) was chosen to subject to a Non-Covalent Interaction analysis, since it was the preferred transition state (lowest energy, as stated before) and beta-methyl styrene was suggested on the instructions page and has been the subject of most of the discussion so far. The fchk. file from this calculation was obtained from the DOI, and cube file generated from the Results/Surfaces-Contours menu in the fchk file. The cube file was generated with a medium grid, saved, and the density cube converted to an NCI surface online. The result could not be made to work as a JMol, but is shown as a JPEG below:

The green surfaces here show attractive intermolecular interactions - these are typically dispersion forces (van der Waals) but can have other origins too. It can be seen by the green 'cloud' in between the two tertiary butyl groups (on the catalyst) that there are attractive dispersion forces between the protruding methyl groups on these parts of the catalyst - this confirms what was outlined earlier when the crystal structure of the catalyst was examined by searching the Cambridge Crystal Database with ConQuest and analysing the results with Mercury - the protruding hydrogens on these groups were found to be approximately 2.6 to 2.7 Angstroms apart - a van der Waals attractive distance.

More important here however, is the interaction between the catalyst and the reacting alkene. A large green 'cloud' can be seen between the phenyl group of beta-methyl styrene and the planar conjugated pi-system on one half of the catalyst. This is only to be expected, as it is well known that pi-electron systems, particularly those in aromatic (cyclic systems) tend to 'stack' and form favourable interactions between molecules - so called 'supra-molecular chemistry'. In an orbital picture, the pi orbitals ('bonds') can overlap and mix, sharing electron density and allowing stabilisation due to electrons now occupying the lower energy (bonding) orbitals of the new, mixed, 'supra-molecular orbitals'.

The most interesting point to note is the extension of the green 'cloud' to cover space between one of the hydrogens on the methyl group of beta-methyl styrene and one of the hydrogens of the cyclohexane ring in the catalyst, adjacent to the Mn centre. This shows another van der Waals dispersion interaction, favourable between these two hydrogens. It should be noted that this is only possible on one side of the catalyst - the aforementioned cyclohexane ring sits in a chair conformation, and its ring flipping motion is restricted by virtue of its bonding to the Mn centre and the large planar pi systems (also bonded to the Mn centre) on either side in the rest of the molecule. This means that on one side, the cyclohexane ring has one axial hydrogen substituent which points 'up' (on the same side of the catalyst as the oxygen which is transferred in the epoxidation reaction), and one axial hydrogen which points 'down' (on the opposite side of the ring to the oxygen which is transferred in the epoxidation reaction). It is the former hydrogen which can share attractive dispersion interactions with the hydrogen on the methyl group in the reacting alkene - on the other side of the molecule this simply is not possible with the 'down' hydrogen, because it is on the other side of the molecule!

This is probably a large contributing factor for the enantioselectivity of the catalyst - since this stabilisation in the transition state is only available on one side, it will be the preferred side for the reaction. The reaction will then only proceed by this route (due to kinetic factors in stabilising the transition state), giving only one product - enantioselectivity. This also shows that an alternative Jacobsen catalyst could be prepared (as such, an enantiomeric form of the catalyst) where the cyclohexane ring sits in its alternative chair conformation, and is then again restricted from ring flipping by its bonding to the rest of the molecule. In this case, the 'up' axial hydrogen is on the other side, and will stabilise and encourage a reacting transition state on the other side of the molecule. This means that it is perfectly set up to selectively epoxidise the other enantiomer of Beta-methyl Styrene, which has a configuration ideally aligned to be stabilised on this (new) side of the molecule.

In conclusion, it can be said that one enantiomer of the Jacobsen catalyst is needed to selectively epoxidise one enantiomer of the alkene. Alternative enantiomers can be prepared for each reaction. The selective Jacobsen catalyst reaction will only proceed with either enantiomer of a trans alkene, since again a trans geometry makes a good dispersion forces fit with the Jacobsen catalyst. With cis alkenes, the configuration is not correct for any of the stabilising interactions described above to take place, and the arguments are invalid. Hence, instead, the Shi catalyst is used for enantioselective epoxidation reactions for different enantiomers of cis alkenes!

The Jacobsen catalyst is also ideally set up in this case for a trans alkene with an phenyl group on one end and a methyl group on the other, since the interactions described above are particular to the substituents in this case. It can be imagined that enantioselectivity would still be shown with other aryl substituents in place of the phenyl group on the alkene, and other alkyl substituents in place of the methyl group, but taken beyond this things are less clear. Substitution of two aryl groups on the alkene, or perhaps the use of a beta-bromomethyl styrene, would probably require the development of a new catalyst as a derivative from the Jacobsen catalyst. This is because, particularly in the case of the bromo-methyl group, steric bulk would probably interfere and again invalidate the above arguments of stabilising the transition states.

QTAIM

There was not time for QTAIM analysis, since even though Avogadro2 worked, there was no display settings button to show the results! I tried to run it on Avogadro1 on the Mac too, but this is taking hours and I am approaching the deadline :(