Rep:Mod:Jab213

All log files can be found here

Introduction

Transition states are the short lived intermediates of a chemical reaction that represent the conformation of the reactants that has the highest energy on the reaction pathway. These species are usually only hypothetical as by their high energy nature, they are almost impossible to isolate and observe in vitro. However the study of these intermediates is important in order to study a reaction as they give important information as to the thermodynamic and kinetic properties of the reaction such as the reaction pathway and activation energy required for it to proceed.

Modelling 'in silica' has therefore been a great bonus to chemistry and the ability to simulate transition states by computational calculation is an increasing powerful tool in any chemists analysis repertoire. In this project, the modelling software of Gaussian 5.0.9 is used to calculate all values using various appropriate basis sets (referred to as 'levels of theory') which operate by applying quantum mechanical theory (solving the Schrödinger equation numerically for multiple atom systems across many geometries; something only a computer can do in any sensible time scale) to a simulated system in order to form a 3D energy plot/surface corresponding to the different relative positions of the constituent atoms.

The two levels of theory used are the Hartree-Fock (HF) and Density Functional Theory (DFT) that differ in that HF calculations do not include electron-electron interactions as it cannot correlate between electrons of different spin in the same orbital. DFT however, takes electron densities into account better and so produces a more accurate model . For HF, a 3-21 basis set was used and for DFT, a 6-31 basis set. This increases the accuracy of the DFT/6-31* calculations but also makes them more computationally demanding (will take more time to calculate). For this reason, the majority of calculations are done in the 'lower' HF/3-21 level of theory.

Nf710 (talk) 15:01, 21 January 2016 (UTC) good intro, electrons of the differnt spin can potentially occupy the same space due to the way a slater determinant is defined

The Cope Rearrangement Tutorial

Optimization of 1,5-hexadiene

Figure 1. Reaction Scheme

Introduction

The Cope rearrangement is a [3,3] sigmatropic rearrangement and belongs to the pericyclic type reaction class. It proceeds in a concerted manner (see figure 1.) in which the bond breakage and formation occurs at the same time through the formation of two distinct transition structures; the boat and the chair. In this section, various conformers of the product of this reaction as well as these two transition structures where modeled and optimised using two levels of Calculation theory (HF/3-21G and DFT/6-31G*)
In order to optimise the starting and finishing reagent (they are the same for this reaction), the lowest energy conformer of many has to be found. In order to do this, many guess structures (either gauche or antiperiplanar with respect to the central C-C bond) were generated and optimised.

Antiperiplanar Conformer

This antiperiplanar conformer was drawn on Gaussview with the dihedral angle set to 180°. The structure was then 'cleaned' (automated setting in the Gaussview program that attempts to crudely rearrange the molecule so that it follows organic chemical convention for bonding and geometry) and then optimised at HF/3-21G level in Gaussian. The resulting energy of the system was given as -231.69097054 a.u. and after the 'Symmetrise' function was applied to it, the molecule had a point group of C₁.

Antiperiplanar 1,5-hexadiene 'anti4'	Results summary

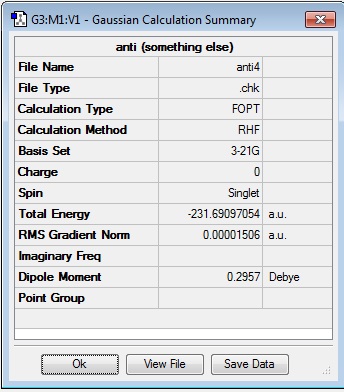This, however is not the lowest energy conformer of 1,5-hexadiene and is identified as the 'anti4' conformation (as classified in appendix 1 of the the lab script).

Gauche Conformer

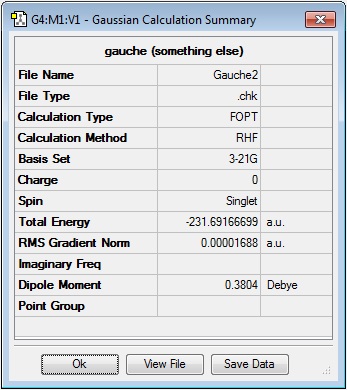
The dihedral angle was then set to 60° and the resulting gauche conformer 'cleaned' and optimised to the HF/3-21G level of theory. The resulting energy of the molecule was -231.69166699 a.u. and the point group C₂. The energy and point group of the molecule indicate that it is the 'gauche2' conformer in the lab script) appendix 1. This molecule has a slightly lower energy than the antiperiplanar conformer before it, this is probably due to the reduction in steric clashing between the terminally bonded carbons and their substituents and the more central ones in the chain as can be seen in the 'anti4' conformation.

Gauche 1,5-hexadiene 'gauche2'	Results summary

Lowest Energy Conformer

Figure 2. 'gauch3' HOMO

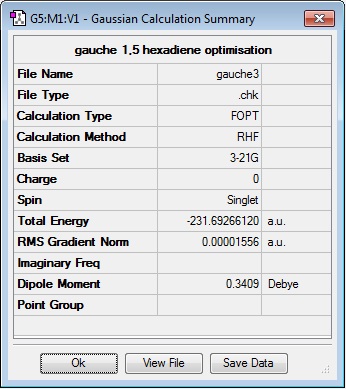
As as prompted by the script, the lowest energy conformation of 1,5-hexadiene (known as 'gauche3') was built, cleaned and set up for optimisation at the HF/3-21G level of theory in gaussview. After the calculation had run, it was found that the total energy of the system was -231.69266120 a.u. with a C₁ point group. This conformer being the lowest in energy would normally seem counter intuitive, as in a gauche conformation, the larger carbon constituents are closer together than in an 'anti' conformation and so you would expect a larger steric clash and subsiquently higher energy. However, if you observe the HOMO molecular orbital (figure 2.) of the 'gauche3' conformer you can see there is a an orbital overlap between the π systems of the terminal carbons, lowering the overall systems energy. Because, this is the lowest energy conformation, this is the most likely state that the molecule will be in at the very start of the reaction and therefore any change in energy that the molecule undergoes will all be relative to this conformer.

Gauche 1,5-hexadiene 'gauche3'	Results summary

Nf710 (talk) 15:03, 21 January 2016 (UTC) Good use of orbitals to explain how they are ordered

Lowest Energy Antiperiplanar Conformer

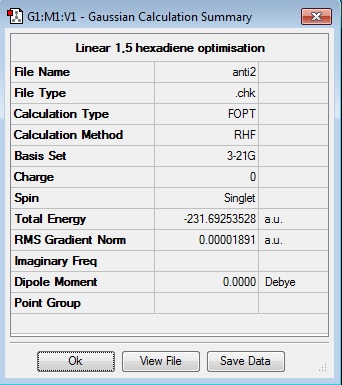
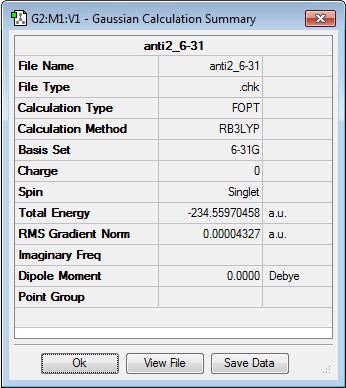
The lowest energy antiperiplanar conformer, 'anti2' was modeled, cleaned and optimised at HF/3-21G. It gave an energy of -231.69253528 a.u. and a point group of C_i. Now the output file of this optimistation was re-calculated using the DFT/6-31G* calculation setup. This re-optimisation gave an energy of -234.55970458 a.u. and again, a point group of C_i.

Antiperiplanar 1,5-hexadiene 'anti3'	Results summary

The relative energies for the two different calculation methods cannot be directly compared due to their differences in approximations used in the calculation. However, the geometries of the two optimised structures can be directly compared. (due to the symmetry of the molecule, only half of the bond lengths and angles have been shown)

	Bond angles (°)				Bond Lengths (Å)
Level of Theory	C1-C2-C3	C2-C3-C4	C1-C2-C3-C4	C2-C3-C4-C5	C1-C2	C2-C3	C3-C4
HF/3-21G	124.8	111.3	114.7	180.0	1.316	1.509	1.553
DFT/6-21G*	125.3	112.7	118.5	180.0	1.334	1.504	1.548

From these, it can be seen that there is only a small differece in the structures therefore the same energy minima on the potential energy surface of the molecule has been converged to. However, the differences do show the DFT/6-21G* optimised structure tp be slightly more more spread out, with larger bond angles and larger C-C double bond lengths.

Nf710 (talk) 15:32, 21 January 2016 (UTC) Your DFT conf. is the wrong energy

Frequency Calculations

Figure 3. IR Spectrum output.

Another check that can be carried out to ensure that an energy minima has been found and not a transition state, is a frequency analysis. Using the DFT/6-21G* calculation setup, a frequency calculation was carried out and Figure 3. shows no imaginary or negative vibrational frequencies and therefore an energy minima, not a transition state, has been found. In this calculation setup, additional information can also be found about the thermodynamic properties of the structure in the output file:

Sum of electronic and zero-point Energies=           -234.416259 a.u.
Sum of electronic and thermal Energies=              -234.408965 a.u.
Sum of electronic and thermal Enthalpies=            -234.408021 a.u.
Sum of electronic and thermal Free Energies=         -234.447881 a.u.

The zero point energy of the molecule has been estimated. The zero point energy of a system is the theoretical energy a system would still contain when the substance was at absolute zero (0K). This value is none-zero as when you apply the quantum harmonic oscillator to the 1,5-hexadiene system, there are no zero energy states available to it. The second value corresponds to the energy of the system at 298.15K (standard conditions), and the 3rd value is a correction for the RT term in H = E + RT(as this is significant at the temperatures considered where it was not at 0K). The final term detailed gives the entropy of the molecule by using thermal correction to Gibbs free energy.

Modelling of Transition States

A transition state by definition is not a minima on an energy surface, but a maxima and therefore cannot be modeled as the reactants previously, by a simple optimisation. The concerted forward reaction of the cope rearrangement can go by two known transition structures, the chair and boat. In order to model and investigate these, an initial allyl fragment was created and optimised under HF/3-21G theory. This fragment was then used to crease the basis for both the boat and chair guess structures.

Chair TS optimization by Force Constant Calculation

The allyl fragments were arranged in a basic chair 'guess' structure with the terminal carbons about 2.2Å away from each other. The symmetrize function on low tolerance was then used and the result was saved as the chair 'guess structure'. This was then used as the basis for a TS(berny) optimisation on the HF/3-21G level of theory with force constants being calculated once. The additional keywords 'Opt=NoEigen' were aslso added to prevent the program from crashing if it calculated negative frequencies (indicative of a transition state of this sort). This program was then run on Gaussian.

Chair Transition structure	Results summary

The energy of the resulting transition state was calculated at -231.61932211 a.u. (significantly higher than the reactants calculated in the previous sections). I addition, a negative vibrational frequency at -817.91 cm^-1 was found which, when observed (see above), is obviously the lead into the cope rearrangement. These prove that a transition state has been found, but not fully confirmed it as the accurate transition structure therefore another method has also been employed to find the Chair TS.

Chair TS optimization by Frozen Coordinate Method

The 'guess' chair structure was taken and both sets of terminal carbons where set as frozen coordinates using the redundant coordinate editor. An optimisation to a minimum was then run using the HF/3-21G level of theory with the program taking into account this modification by including opt=modredundant within its keywords. From the output file, the previously frozen coordinates were unfrozen and set to 'derivative' in the redundant coordinate editor and the file was then set up to optimise to a TS(berny). This was again run at the HF/3-21G level of theory and the results showed a very similar energy (-231.61932232 a.u.) , geometry and vibrational frequency to the previous force constant calculation (data can be found here). As the same level of theory (therefore the same approximations about the system were made during calculation) the energies of the two methods can be directly compared and as the energy gap between the two systems was negligible (2.1x10^-7a.u.) we can assume the same point on the energy surface (ie, the chair transition structure) has been converged to successfully.

Boat TS optimization by QST2&QST3 Methods

For the modelling of the boat transition structure, a boat guess transition structure was initially formed from two of the optimised allyl fragments arranged on top of each other and then optimsed in the same method as used for the chair TS. however, this did not work as the gaussian program optimised the structure back into the chair conformation. A QST2 method approach was then used. This requires the creation of the reactant and product molecule from which the program would find an intermediate. To this end, The previously optimised 'anti2' conformer of 1,5-hexadiene was taken as the reactant and then the numbering of the atoms making up the molecule were edited to reflect the product if this conformer underwent a cope rearrangement (figure 4.).

Figure 4. labelled reactants and products

A QTS2 calculation was then set up and run at the HF/3-21G level of theory. This also was optimised to the same point on the energy surface as done previously for the chair conformation and gave very similar energies and geometries to that of the previous chair calculations:

Failed Boat TS.	Results summary

The dihedral angle of the central C-C bond was then altered from the antiperiplanar conformation of 180° to 0°. When the same calculation was now run, a boat transition structure was formed. The energy of the system was given at -231.60280230 a.u. and a single negative vibrational frequency was found at -840.25 cm^-1 confirming that the structure formed is a transition state.

Boat Transition Structure	results summary

Boat TS optimisation by IRC Method

To help visualise and calculate the trajectory of a reaction pathway, an Intrinsic Reaction Coordinate (IRC) can be set up. This method calculates the lowest energy path (ie the steepest gradient down the energy surface from the maxima of the transition state) from the transition state to the product molecule. An IRC calculation was then set up using the optimised Chair TS from the previous frozen coordinate setup and set for 50 steps with force constants being measured at each step. Due to the symmetry of the cope rearrangement reaction under study (the reactants and products are the same), the program was set to run in the forward direction only.

Reaction Coordinate Visualisation.	Results summary

The IRC plot clearly shows how the calculation reached a minima in energy and the animation shows how this was achieved by the small incremental changes in the geometry of the molecule leading to an energy drop. The energy plateaued on the graph and the calculation stopped at point 44 implying that a full minima was found. The data for this 44th step is displayed in Figure 5.

Figure 5. Final IRC Product

The energy of this product was given as -231.69157881 and it also had a C₂ point group. This identifies it as the 'gauche2' conformer of 1,5-hexadiene optimised earlier and also confirms that an energy minima (if not the lowest conformer) has indeed been reached.

correct conformer, you could have shown the gradient graph

Activation Energy Calculations

To accurately compare the energies of the chair TS, boat TS and starting molecule, all of them were re-optimised from the previous HF/3-21G files to the DFT/6-31G* level of theory which, as discussed in the introduction, will give more accurate results. This resulted in a slight change of geometry across the molecules:

	Boat TS		Chair TS
Level of Theory	C-C Bond (Å)	C C Gap (Å)	C-C Bond (Å)	C C Gap (Å)
HF/3-21G	1.381	2.140	1.389	2.020
DFT/6-21G*	1.395	2.257	1.406	1.984

The Geometrical change of the molecules is however is insignificant between the 2 levels of theory and therefore it can be concluded that the two levels can be used interchangeably when the objective of the calculation is to find the spacial coordinates of a molecule. The real difference between the two methods is in the energies computed for the system which are summarised in this table:

	HF/3-21G			DFT/6-31G
	Electronic Energy (a.u.)	Sum of Electronic and Zero Point Energies (a.u.)	Sum of Electronic and Thermal Energies (a.u.)	Electronic Energy (a.u.)	Sum of Electronic and Zero Point Energies (a.u.)	Sum of Electronic and Thermal Energies (a.u.)
'anti2'	-231.692535	-231.539539	-231.532565	-234.559705	-234.416259	-234.408965
Chair TS	-231.619322	-231.466699	-231.461341	-234.50545061	-234.362592	-234.356689
Boat TS	-231.602802	-231.450928	-231.445299	-234.492899	-234.351374	-234.345059

To find the activation energy required for a reaction to proceed by that specific transition state, the energy of the Transition state at a specific temperature has the energy of a typical stating material subtracted from it (in this case the previously investigated 'anti2' conformer as it has already been analysed at both levels of theory investigated here). The remaining energy is therefore the energy difference between reactant and transition state and can be converted from a.u. to KJ mol^-1 by multiplication (factor 2625.50 used).

As expected,the activation energies from both levels of theory show that the boat transition structure requires more energy to be reached and therefore the chair TS is most likely to be the reaction path that the molecule takes as it undergoes a cope rearrangement. There is however a large difference in calculated energies between the different levels of theory used in the calculations, with the HF/3-21G giving on average much higher energetic estimates for the activation energy. When compared to the literature values of 140.16 ± 2.09 and 187.02 ± 8.37 for the chair and boat structures respectively , it can be seen that the DFT/6-31G* level of theory gives an accurate estimation of the energies while the HF/3-21G method is out by approximately 50KJ mol^-1.

To conclude, while both levels of theory give very similar geometries with minimal differece between them, the energies calculated by the 'lower' level of theory HF/3-21G can only be used for relative comparisons and do not reflect accurate in lab results. The 'higher' DFT/6-31G* level of theory on the other hand can be used to accurately measure both withing a good tolerance but given its longer run times may be reserved for final optimisations where faster, lower level calculations can be run before it. Nf710 (talk) 15:39, 21 January 2016 (UTC) You have shown some good basicundertsanding of the methods. unfortunatly you got the anti conf. energy wrong. It should be slightly lower. Other than that you have done everything that was asked of you

Exercise: The Diels-Alder Cycloaddition

Like the Cope rearrangement, a Diels-Alder cycloaddition is a pericyclic reaction that proceeds in a concerted manner. The reactants, typically an electron rich diene and an electron poor dienophile, undergo a [4+2] cycloaddition in which the formation of two new σ C-C bonds at the expense of two π C-C bonds is the main enthalpic driving force of the reaction. In this section, two Diels-Alder reactions will be investigated, a symmetric addition of cis-butadiene and ethene, then the reaction of cyclohexa-1,3-diene with maleic anhydride.

Butadiene, Ethene Reaction

A molecule of cis-butadiene was modeled on gaussview, 'cleaned', 'symmetrised' and then optimised to a minimum using the standard HF/3-21G gaussian program. Using the product file, the molecular orbitals of the molecule where then visualised. The HOMO and LUMO with cartesian axis are displayed below:

	Activation Energies (KJ mol-1)
	HF/3-21G		DFT/6-31G
	At 0K	At 298K	At 0K	At 298K
Chair TS	191.24142	186.998612	140.9027085	137.250638
Boat TS	232.6481805	229.116883	170.3555675	167.785203

HOMO	LUMO

As can be seen, the HOMO (energy given at -0.32539 a.u.) is antisymetric about the XY and YZ plane while the LUMO (energy given at 0.12366) is symmetic about the the XY and YZ planes. The overall point group of the molecule was C_2v. In a typical Diels-Alder reaction, the HOMO of the diene (shown) will interact with the LUMO of the dieneophile (simple antisymetric π* orbital). This will be observed as mixing of these orbitals in the transition structure HOMO and LUMO, analysed later in this report. This mixing can usually occur due to the effects of the groups attached to the active parts of the reagents; ie, the electron withdrawing groups on the dienophile lower its LUMOs energy while EDG's on the diene raise the energy of its HOMO allowing for more equal energies of the mixing MO's and therefore a larger stabilisation by forward reaction.

Optimization of Reactants

The optimized structure of the cis-butadiene and an optimised structure of ethene where created using the AM1 semi-empirical molecular orbital method. They had the have the following output energies.(see calc summaries here)

Ethene	cis butadiene
0.02619024 a.u.	0.04879724 a.u.

Optimization of Transition Structure

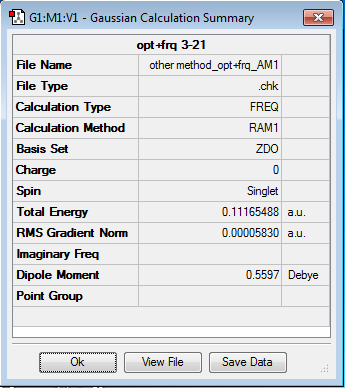
The optimised reactant fragments where then placed in the same gaussian window and arranged so that the terminal carbons where 2.2Å apart. The set was then, cleaned and symmiterised. Using the frozen coordinate method (described when finding the chair transition state previously), the transition state for the reaction was found using the TS(berny) calculation setup and AM1 basis set. The energy of the system was reported at 0.11165488 a.u. and an imaginary (negative) vibrational frequency was found at -956.36 cm^-1.

Transition Structure	Results summary

Figure 6. First Posative Vibrational Frequency Animation

The presence of the negative vibrational mode (bond forming in nature) confirms that a transition structure has been found. Figure 6. shows the lowest energy, real vibrational mode of the transition structure at 146.41 cm^-1 which is a rock of the transition state.

(What are the properties of this negative vibrational mode? How do the C-C lengths correspond to typical C-C bond lengths and their combined VdW radii? Tam10 (talk) 16:00, 12 January 2016 (UTC))

IRC Reaction Pathway

An IRC calculation at the AM1 level of with 90 steps in both directions (as unlike the cope rearrangement, the products and reactants are not the same therefore we need the calculation to find both) was then run on the optimised transition structure. A problem arose in that the calculation ran a dissociation therefore both the animation and the energy graph show the scheme as going from product to reactants. Both the products and the reactants plateau therefore stable minima have been found.

IRC Reaction coordinate animation	IRC Energy pathway

MO Analysis

The HOMO and LUMO of the transition state were also analysed. As predicted by the Woodward-Hoffman rules, the orbitals of the same symmetry (the antisymmetric HOMO of the butadiene and antisymmetric LUMO of ethene forming the again antisymmetric HOMO of the TS) mix together to give the HOMO and LUMO of the transition state. The energies of the HMO and LUMO were found to be -0.32393 a.u. and 0.02314 a.u. respectively.

HOMO	LUMO

Maleic Anhydride, cyclohexa-1,3-diene Reaction

A simple Diels-Alder reaction performed in the lab by heating the reagents together, the maleic Anhydride, cyclohexa-1,3-diene reaction is a good example of the EXO/ENDO selectivity of the Diels-Alder reaction. This is the observation that the 'endo' product is usually favoured by this reaction due to suspected secondary orbital interactions. The reaction proceeds so well practically in the lab (with high yields and fast reaction times) due to the comparatively low electron density of the double bond (dienophile) in the maleic anhydrid caused by the electron withdrawing substituents of the compound.
Before any transition states could be computed, the initial reactants were modelled and optimised using the AM1 level of Theory. Their energies we as follows*:

Maleic Anhydride	Cyclohexa-1,3-diene
-0.12182423 a.u.	-230.5396093 a.u.

(The cyclohexadiene looks like it was calculated with HF, not AM1 Tam10 (talk) 16:00, 12 January 2016 (UTC))

*Link to the react summarys can be found here

ENDO transition State

Figure 7. Negative Vibrational mode at -806.37cm^-1

The ENDO product is so named as due to secondary orbital interactions, the transition state of the reaction lies at a lower energy than that for the EXO despite the fact that the final ENDO product, due to steric clashing is no the thermodynamically most stable product.

(This is a bit of a confusing sentence. It is called endo as the -C(=O)-O-C(=O)- is underneath the diene. Also, have you done calculations on the product to confirm that? Tam10 (talk) 16:00, 12 January 2016 (UTC))

To find the transition structure, a guess structure was generated in which carbonyl carbons in the maliec anhydride ring where lying over diene. The C which were to end being bonded where then set to 2.2Å apart and using the frozen coordinte method detailed earlier, the transition state was generated by a TS(berny) calculation at the AM1 level of Theory. This was then re-optimsed to a TS using the force constant and frequency analysis to give the negative vibrational frequency (indicative of a transition state) at -806.37cm^-1, shown in Figure 7 and an energy of -0.05150480 a.u.

Transition Structure	Results summary

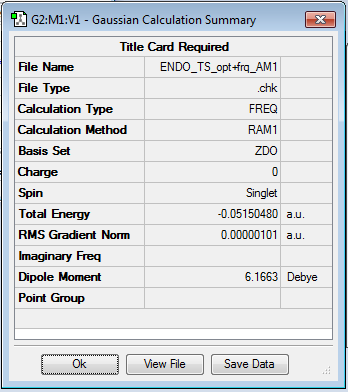Using the optimised transition state as a starting point, an IRC in both directions with 90 points was run at the AM1 level of Theory and the above reaction coordinate was the result. The Energy for the reactants and products plateaued so minima were formed and it is clear how the ENDO product is formed.
In addition to the IRC, the actual Geometries and the Molecular Orbitals of the transition state were noted and will be compared to those of the EXO product later in order to explain the behaviour of the system.

EXO transition State

The EXO product was analysed using the same method as the ENDO product save that the initial starting position of the maleic anhydride was rotated 180°. The final optimisation of the transition structure gave a negative vibrational frequency at -812.27cm^-1 and an overall energy of the system of -0.05041985 a.u. The animation of the negative vibrational frequency can be found here and the following table gives the results of the TS(berny) calculation at the AM1 level of theory.

Transition Structure	Results summary

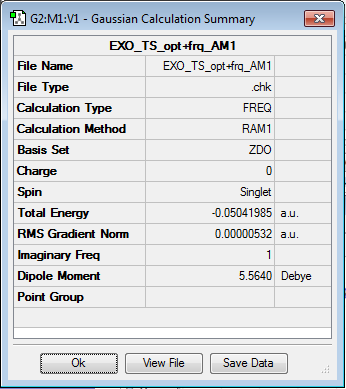As with the ENDO, a 90 step, two directional IRC was calculated to illustrate the reaction coordinates. The above graph and illustration show the inverse of the reaction with reactant being formed out of the products. Despite this, the IRC did reach an energy minima (plateau on the graph) an it does show the manner in which the reaction proceeds and therefore is still relevant to the project. As before, The MO's as well as selected geometries of the molecule were recorded.

Comparison of Different TS

The geometries of the two transition states were compared. As a general rule, the bonds in the forming ring ranged at about 1.4 Å for both previously single and double bonds showing that the electrons around the ring had been de localised and the bonds themselves were in between single and double. The forming bond (C1-C17) is larger than a single bon but is significantly shorter than two times the van der waals radii of a Carbon atoms (1.70 Å) once again showing a bond is being formed.

ENDO		EXO
C1-C17	2.16239	C1-C17	2.17055
C16-C17	1.40849	C16-C17	1.41011
C2-C3	1.39724	C2-C3	1.39675
C18-O23	1.22057	C18-O23	1.22053
C1-C2	1.39305	C1-C2	1.39437
C1-C12	1.49053	C1-C12	1.48975

The overall Geometries of the Transition structures are not that different, yet there is still a marked difference in the energies of the transition structures. These are relative energies only and con only be used for a general comparison of states as the low level of theory used in this section (AM1) does not give accurate energies corresponding to real world measurements. For accurate energy calculations, a higher level of theory would be required (ie the DFT/6-31G* used in the previous Cope Rearrangement section)

(Perhaps include some more detail about the steric clashes between the substituents Tam10 (talk) 16:00, 12 January 2016 (UTC))

Transition State Energies (a.u.)
ENDO	EXO
-0.05150480	-0.05041985

The ENDO transition structure is clearly lower in energy and as the reactants from which these structures will be formed are the same (ie, the same starting energy) then the activation energy required to get to the ENDO TS will be less than for the EXO. This means that the ENDO product will be kinetically favored and under kinetically controlled conditions (low temperature, fast, irreversible reactions) the ENDO product will be formed over the thermodynamically more stable EXO product.
The reason that the ENDO TS is lower in energy is due to secondary orbital interactions between the C=O π* orbitals in maleic anhydride and the C=C π orbitals of cyclohexa-1,3-diene which form the orbital modeled below (LUMO+1). This interaction is stronger in the ENDO TS than in the EXO TS (as the mixed orbital is still visible in the corresponding EXO LUMO+1 orbital) because of the way in which the ENDO structure is arranged, means the mixing orbitals are closer in space and therefore form a better overlap and therefore a stronger (lower in energy) interaction unlike the EXO which is further apart therefore more diffuse and higher in energy.

	HOMO	LUMO	LUMO+1
ENDO
EXO

Conclusion

In sum, three different pericyclic reactions have been studied through the course of this experiment; the cope rearrangement of 1,5-hexadiene and the diels alder cycloadditions of cis-butadiene with ethene and maleic anhydride with cylcohexa-1,3-diene. All of these have been relatively successful and the techniques used in this lab can be used in the future and be applied across a large range of chemistry.

In the tutorial section, the HF/3-21 and DFT/6-31 theory level were shown to be a powerful computational methods. The 'gauche3' conformer of 1,5-hexadiene was found to be the lowest energy and activation Energies for the reaction through both the Chair and Boat transition structures have been calculated and come relatively close to the literature values showing confirming the use of this modelling software.

The use of Molecular orbital analysis to confirm the manner in which orbitals of ethene and cis-butadiene mix and from that to explain the transition structure with reference to its symmetry and Woodward-Hoffman rules was achieved as well as the Transition structure being fully characterised. Further analysis into the activation energies of this process and the effects of adding electron withdrawing or donating substituents onto the reactant molecules would be an interesting avenue of study and would give a more complete picture of how Diels-Alder process occur and what differences to the system would have the largest impact on it.

Finally the ENDO/EXO selectivity of the maleic anhydride with cylcohexa-1,3-diene reaction was investigated. The different transition states of the reaction were fully characterised and it was shown how secondary orbital interactions forming molecular orbitals in the transition state can stabalise the TS and therefore reduce its energy meaning that the ENDO product is favored when the reaction is carried out in the lab. Further analysis of this section could be carried out at a higher level of theory so that the energies calculated are closer to literature reports instead of being used (as they are here) just as relative comparisons to each other.