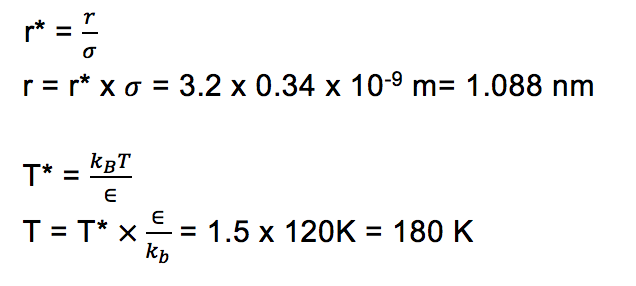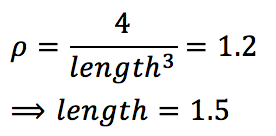Rep:Mod:JYC214
General comments: This report is pretty poor, no explanations, missing tasks and results that lead a little to be questioned [for example, your 'gas' rdf is liquid.... Mark: 20/100
Introduction to Molecular Dynamics Simulation
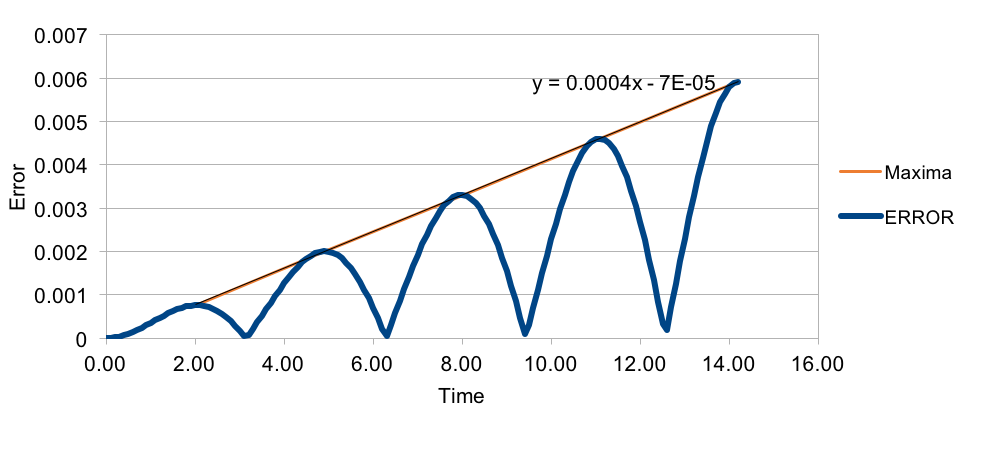
An error-time graph is plotted and the maxima is identified. The values of the maxima appear to be in good fit to a linear model with equation y=0.0004x.
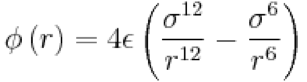
Under standard conditions, ie 298 K and 1atm,
Number of moles of 1 mL of water, n = 1/18 = 0.056 moles
Number of molecules, N = n x NA = 0.056 x 6.022e23 = 3.346e22 Tick
Number of moles of 10000 water molecules = 10000/6.022E23 = 1.66e-20 moles
Volume of 10000 water molecules = 1.66e-20 x 18 = 3e-19 mL Tick
As a point (0.5, 0.5, 0.5) moves along the vector (0.7, 0.6, 0.2), with periodic boundary conditions applied, it will end up at (0.2, 0.1, 0.7). Tick
Giving atoms random starting coordinates causes problems in simulations as when two atoms happen to be generated close together, repulsion between the 2 atoms will cause potential energy to increase dramatically and hence causing discrepancies in simulation calculations.At these distance, importantly, the timestep needs to be sufficiently small to prevent the system from "blow-up"
As a simple cubic lattice has only one lattice point per unit cell,
A face centred cubic has 4 lattice points per unit cell,
As a box of simple cubic lattice contains 1000 (10x10x10) unit cells, and so contains 1000 lattice points; A face centred cubic lattice would result in 4000 atoms.
When we are specifying ![]() and
and ![]() , we use the velocity Verlet algorithm.
, we use the velocity Verlet algorithm.
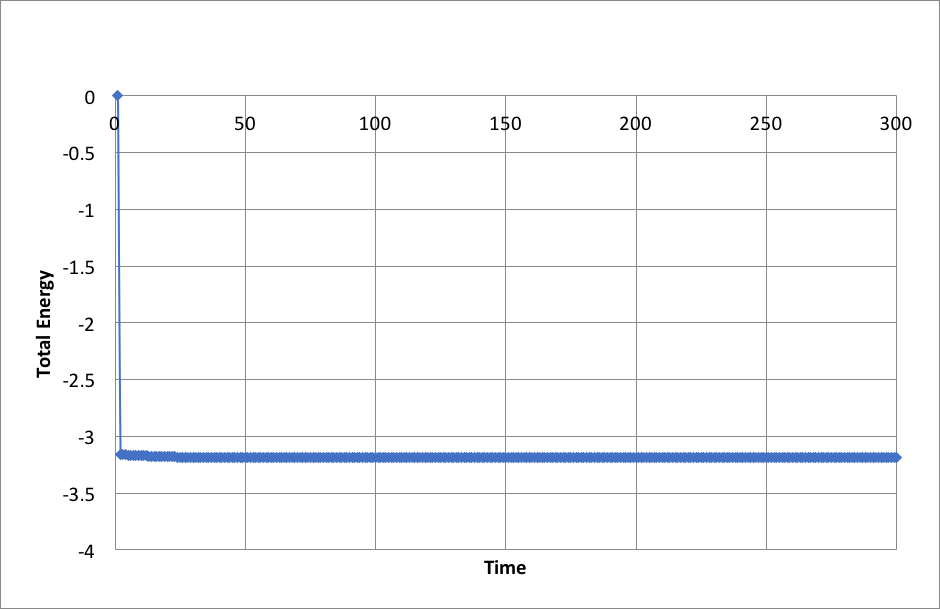
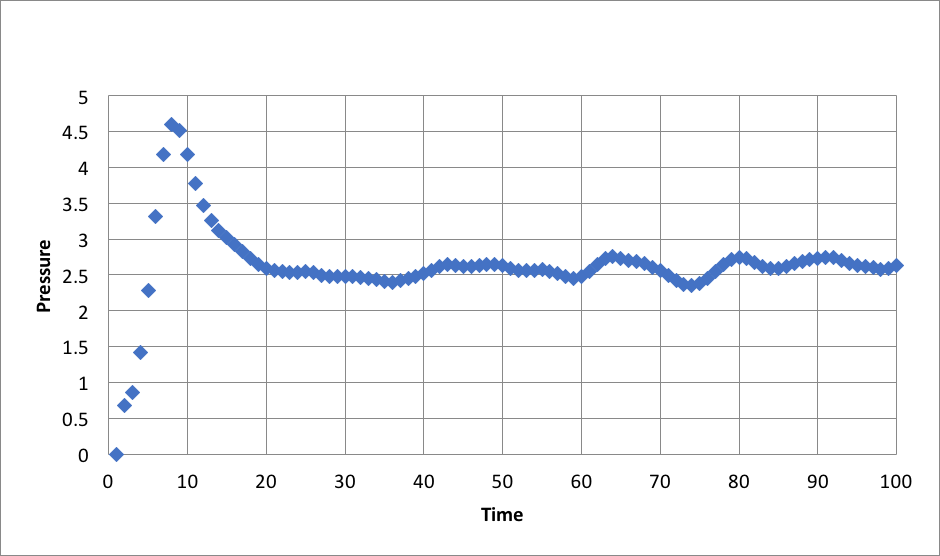
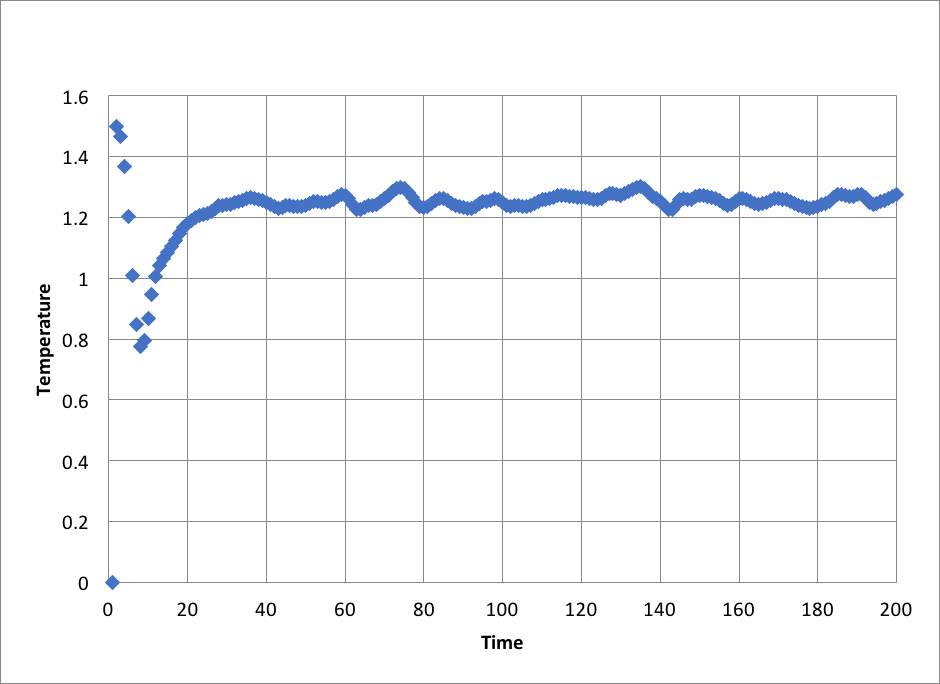
Plots of the energy, temperature, and pressure, against time for the 0.001 timestep experiment:
Running Simulations under Specific Conditions
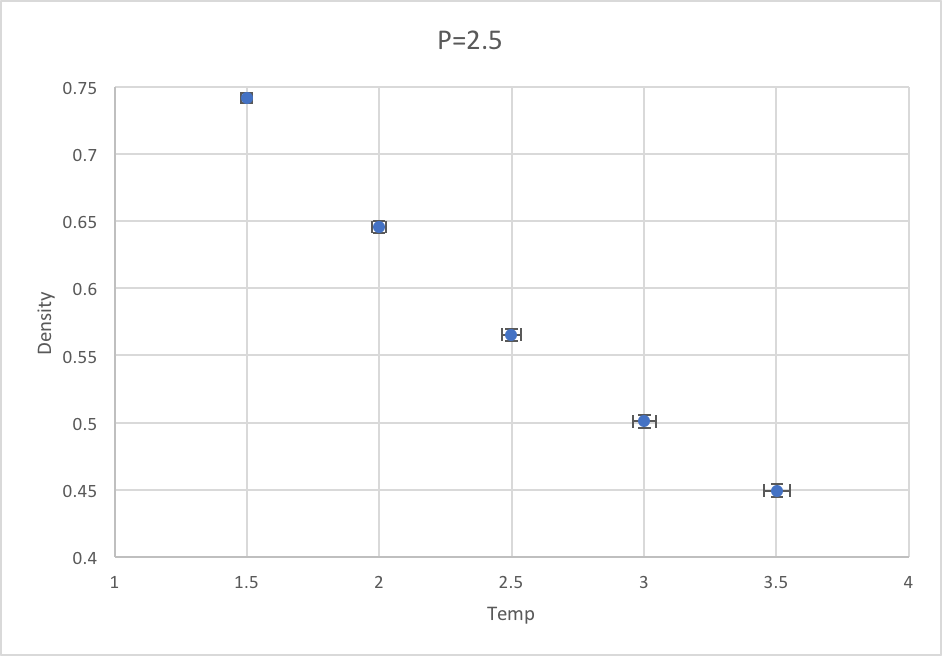
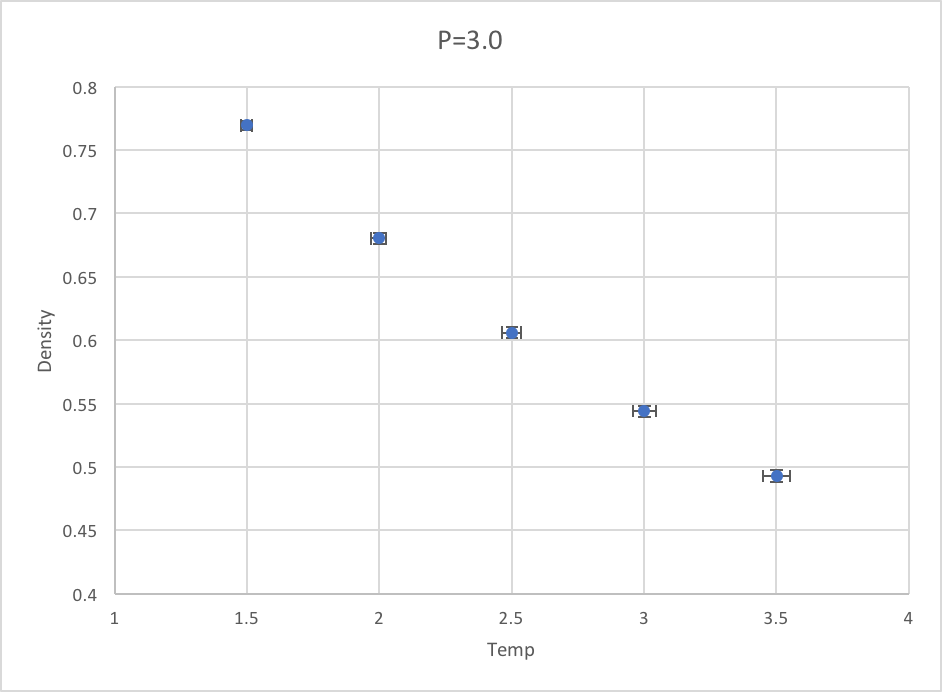
Plotting the Equations of State
Density against temperature for pressures at 2.5 and 3.0:
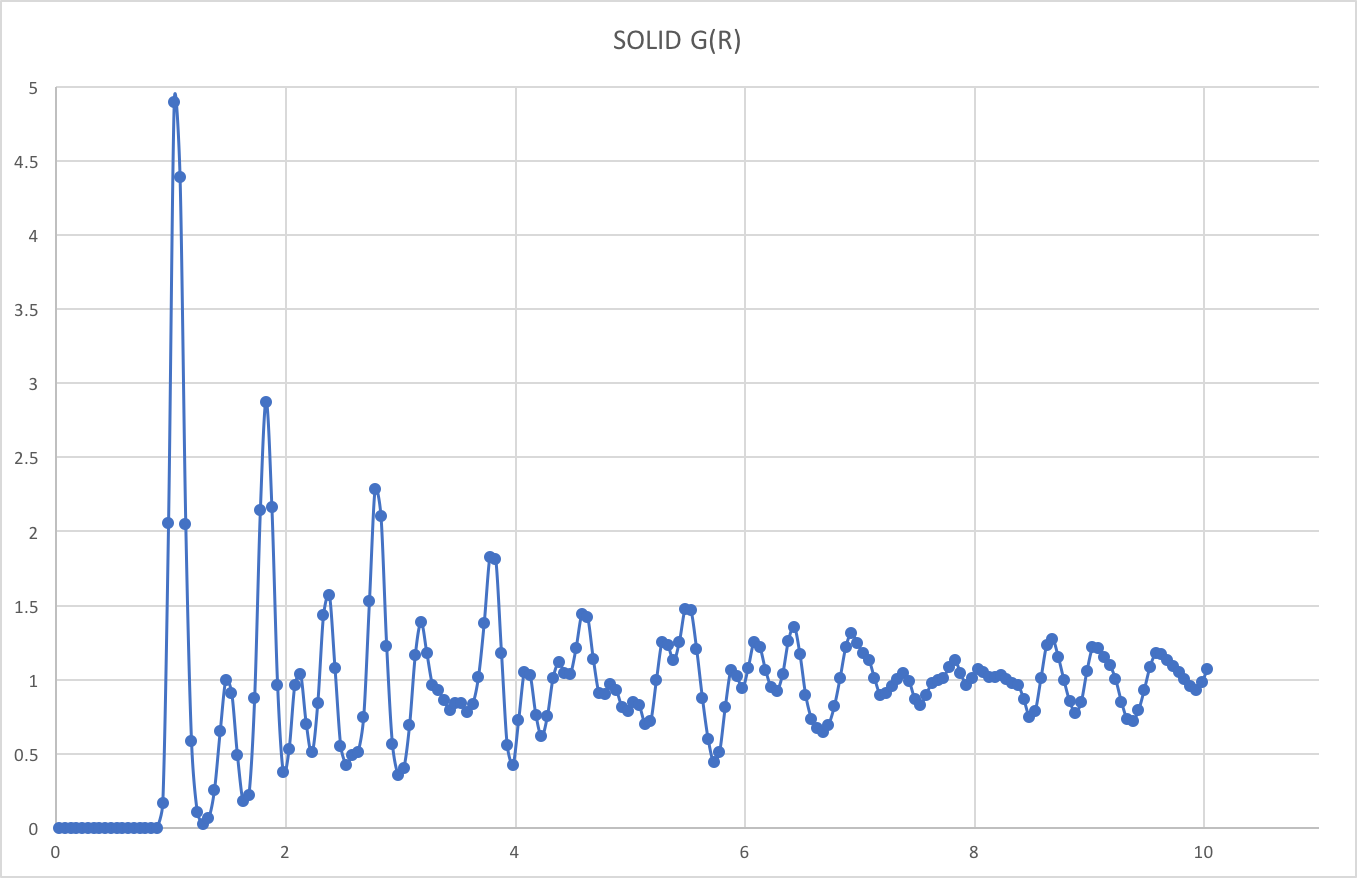
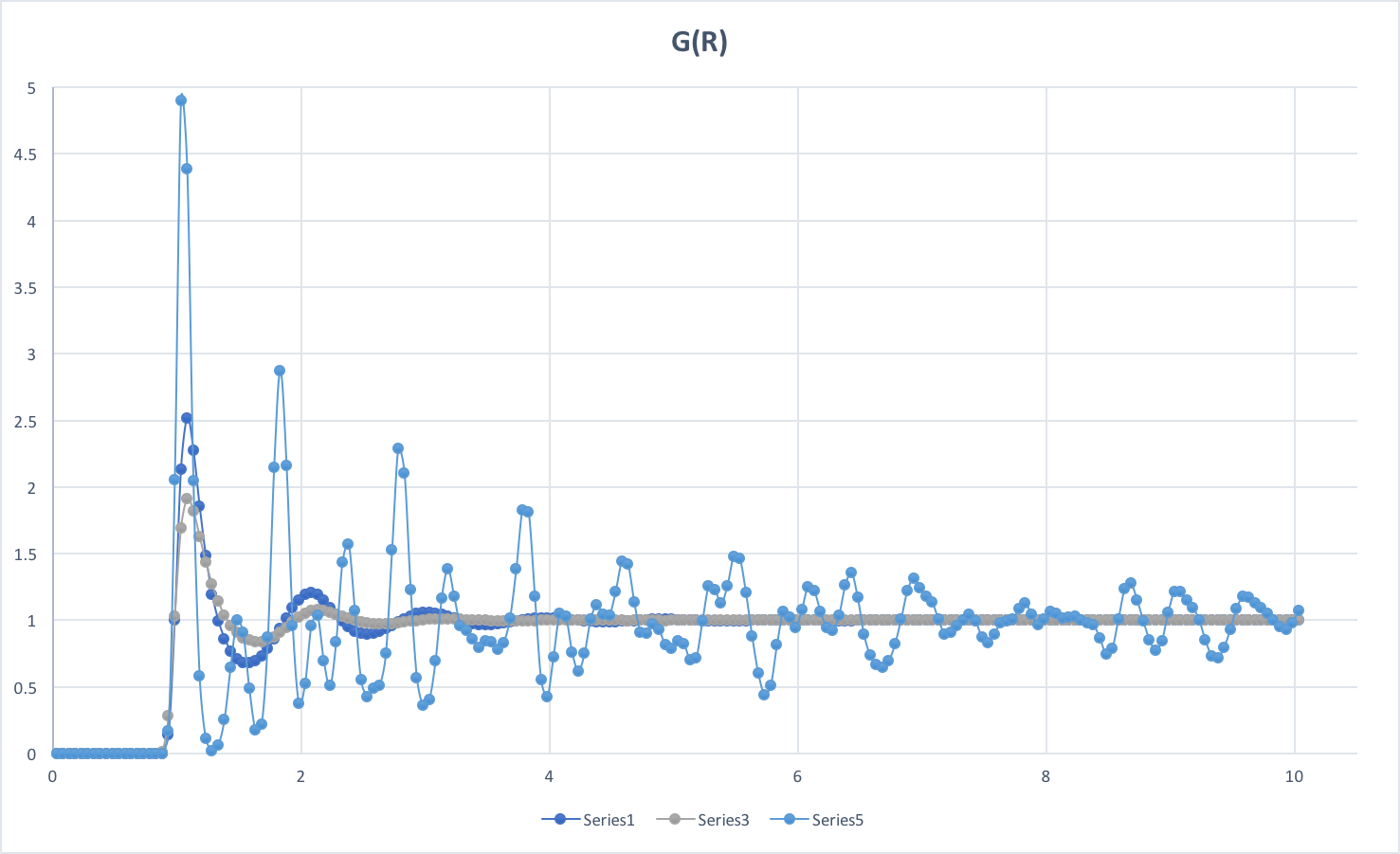
RDFs for simulations of the Lennard-Jones system in the three phases:
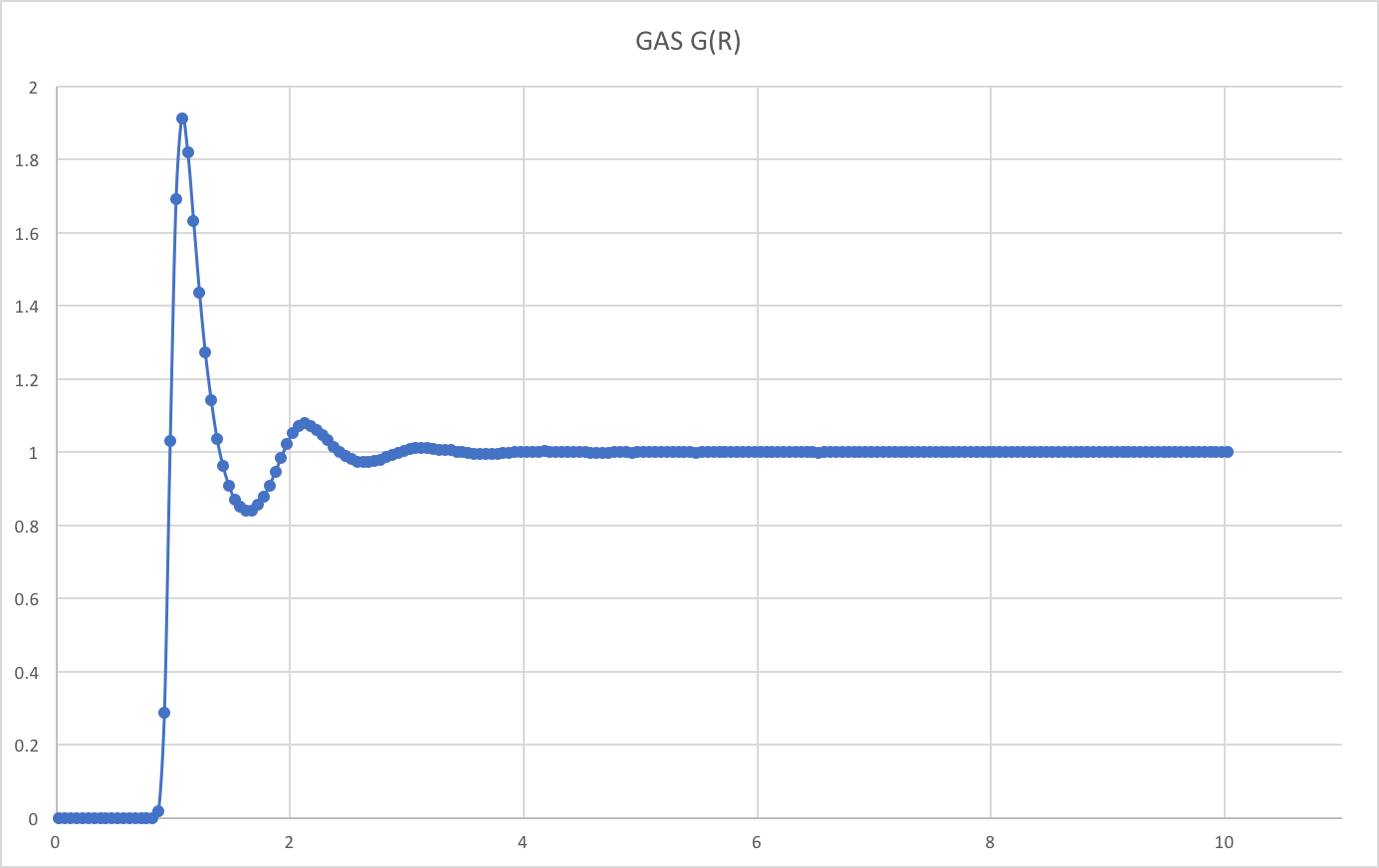
There is essentially zero probability of finding particles at distances less than about 1.0Å from each other. This is due to the presence of very strong repulsive forces at short distances.