Rep:Mod:JS6313 TS
Introduction
[SAMPLE]
Units
In this article, energies are given in atomic units of energy, a.u,; 1 a.u. is equivalent to 1 hartree which is defined as R∞hc, where R∞ is the Rydberg constant, h is Planck's constant and c is the speed of light in a vacuum. This comes out as 1 a.u. = 4.359 744 650 x 10-18 J.[1]
Cope Rearrangement (Tutorial)
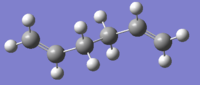
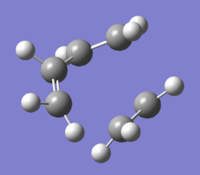
Optimisations in this section have been carried out using the Hartree-Fock method and the 3-21G basis set. The first two calculations were for 1,5-hexadiene in the anti and gauche conformations, both of which were found to have C1 symmetries. As expected, the anti conformation was found to have a slightly lower energy, which can be attributed to steric clashing between carbons 2 and 4.
The conformation which would be expected to be the lowest in energy, taking into account only sterics, is anti when viewed along carbons 3 and 4. This turns out not to be the case; in fact, it is when the substituents on these carbons are in a gauche to each other.
| Processed Model | Symmetry | Energy (a. u.) | Relative Energy (kcal/mol) | Manual Wiki Structure |
|---|---|---|---|---|
 |
C1 | -231.69097049 | 1.07 | anti4 |
 |
C2 | -231.69166702 | 0.63 | gauche2 |
 |
C1 | -231.69266119 | 0.00 | gauche3 |
 |
Ci | -231.69253528 | 0.08 | anti2 |
The anti2 conformation only changes slightly when run at the DFT level of theory and a 6-31G(d) basis set. All angles are within 0.6° of their corresponding angles on each basis set. These are the various values found in the output file of the optimised and frequency analysed anti2 conformer:
| Value | Energy (a.u.) |
|---|---|
| Sum of electronic and zero-point energies | -234.469214 |
| Sum of electronic and thermal Energies | -234.461866 |
| Sum of electronic and thermal Enthalpies | -234.460922 |
| Sum of electronic and thermal Free Energies | -234.500798 |
Optimising the "Chair" and "Boat" Transition Structures
The first guess at a chair transition state for two C3H5 fragments gave the expected singular imaginary frequency at -818 cm-1; this shows that the optimised structure
is at a potential energy maximum saddle point. Any disturbance from this state would result in either product or back to reactants.
Fixing the forming/breaking bond lengths at 2.2 Å ran as expected; the terminal distances were in fact 2.2 Å and 2.27 Å. Upon fixing the hessian and using 'derivative' as opposed to 'add', the structure did not visibly change but the bond angles changed to 2.21 Å and 2.25 Å.
Diers-Alder Cycloaddition
 |
 |
The HOMOs shown here are antisymmetric with respect to the plane of the cis-butadiene molecule.
- ↑ http://physics.nist.gov/cgi-bin/cuu/Value?hr