Rep:Mod:JR5225
Jack Rogan - Module 1
Part 1: Molecular Mechanics
Objectives
The use of molecular mechanics to model, and predict the geometry and regioselectivity of two environments:
- During a cyclopentadiene dimer hydrogenation reaction.
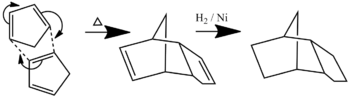
Scheme for the diene dimer hydrogenation - The conformation/atropisomerism of a large ring ketone - an intermediate in a Taxol synthesis.
The estimated time for completion: From project brief, < 6 hours.
Molecular Mechanics
The molecular mechanics method is used for finding the molecular properties and three-dimensional effects of many molecules. It involves deriving these properties given that the energy of the system can be accurately approximated without finding electronic wavefunctions for the system. This means assuming that the energy can be calculated by finding the sum of the contributions by the stretching of, distortion of, and the torsion around the applicable bonds, and the sum of all electrostatic and Van der Waals interactions. All of these can be quickly and easily calculated from the known data of many compounds.
Thus, using the molecular mechanics model, it is possible to accurately assess the energy, geometry, and even stability of a compound without performing quantum-mechanical operations. However, this method does suffer limitations: it is limited by the use of experimental or otherwise known data to calculate its parameters, therefore, it cannot accurately be used to model new or undocumented compounds, or model states (e.g. transition states or transient intermediates) where the properties cannot currently be sufficiently measured.
Cyclopentadiene Dimer Hydrogenation
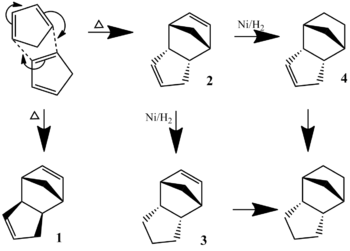
When cyclopentadiene dimerises under heating, it almost exclusively forms the endo-dimer, 2, rather than the exo dimer, 1. This can then be hydrogenated, initially to either of the dihydro derivatives, 3 or 4, but the tetrahydro derivative, can be formed after a longer period of hydrogenation.
An MM2 method was used to model the comparative stability of compounds 1, 2, 3, and 4:
Results
| Compound | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|

|

|

|

| ||
| Contributions / kcal mol-1 |
Stretch | 1.2850 | 1.2507 | 1.2353 | 1.0969 |
| Bend | 20.5783 | 20.8476 | 18.9391 | 14.5264 | |
| Stretch-Bend | -0.8382 | -0.8358 | -0.7610 | -0.5492 | |
| Torsion | 7.6559 | 9.5109 | 12.1231 | 12.4986 | |
| Non-1,4 Van der Waals | -1.4167 | -1.5430 | -1.5011 | -1.0728 | |
| 1,4 Van der Waals | 4.2346 | 4.3195 | 5.7282 | 4.5115 | |
| Dipole-Dipole | 0.3775 | 0.4476 | 0.1631 | 0.1406 | |
| Total Energy / kcal mol-1 | 31.8765 | 33.9975 | 35.9266 | 31.1521 | |
| Compound 4 bond angle, from ChemBio3D | |
 |
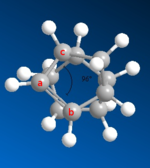 |
The results show that the exo dimer is lower in energy - as modelled by the MM2 method - than the endo dimer by over 2.1 kcal mol-1. However, it is known that the reaction exclusively forms the endo dimer in lab conditions. The fact that the exo dimer is lower in energy, and therefore more stable, show that it is favourable thermodynamically. Therefore, it can be deduced that the dimerisation of cyclopentadiene proceeds under kinetic control.
This is supported by the taking into account Secondary Orbital Interactions (SOIs) between pz orbitals in the transition state.[1] The interaction between these overlapping orbitals significantly lowers the energy of the potential surface, so the transition state leading to the endo dimer is kinetically favoured.
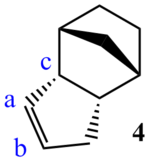
The first hydrogenation products, molecules 3 and 4, differ in stability by 4.8 kcal mol-1, this is largely due to the bending energy: 18.9 kcal mol-1 and 14.5 kcal mol-1, respectively. This difference (4.4 kcal mol-1 is not only the main part of the difference, but a significant proportion of the total bending energy: 30.3 % of that of compound 4. The reason for this difference is that compound 3 contains the very strained double bond between atoms a and b, 96° between atoms c, a and b, as opposed to a preferred sp2 angle of 120°. The sp3 bond in compound 4 is less strained, as its preferred angle is about 109.5°.
Taxol Intermediate
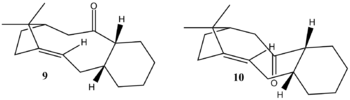
In the sythesis of Taxol, a major intermediate involves the synthesis of what is originally made as compound 9. This isomerises to compound 10 when left to stand - this is known as an atropisomerism. In this case, the Molecular Mechanics model was once again used to determine the relative stability of the two isomers, in order to determine why this occurs in this particular case.
Results
| Compound | 9 | 10 |
|---|---|---|
 |

| |
| Relative Energy / kcal mol-1 | 53.3044 | 42.6829 |
| Steric effects in Taxol intermediates | |
 |
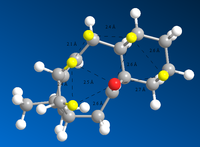 |
Compound 10 is more stable by 10.6 kcal mol-1 - 25% of the total. This can be explained, in terms of the non-quantum mechanical model used here - which will not take into account orbital effects, by the steric effects that the atropisomers experience. In molecule 9, the "upwards"-facing oxygen has the effect of forcing the atoms on the other side of the molecule into close proximity, whereas in molecule 10, the oxygen is in the same region, and the atoms are all much less sterically destabilised. For example, in molecule 9, the average H-H distance in the region is approximately 2.2 Å. Compared to the average for compound 10: 2.4 Å, and the combined Van der Waals radii - here used to approximate the optimum distance - 2.4 Å[2], it is clear that the Hydrogen atoms in 9 are more sterically destabilised. In addition, the average H-Cl distance in this region of 10 is 2.6 Å, close to the optimum distance - from the Van der Waals radii - of 2.7 Å[2]. This is likely to have a stabilising effect on Molecule 10.[3]
Part 2: Semi-empirical Molecular Orbital Theory.
Objectives
The use of models taking into account electron effects and molecular orbitals:
- Investigating how the electronic interactions affect the energy and geometry
- Investigating reactivity and the effect of Molecular orbitals and charge density
The estimated time for completion: From project brief, ~12 hours.
Regioselective Addition of an Electrophile to a Diene

| |||
| Overlay of Geometries |
When an electrophilic reagent such as dichlorocarbene reacts with a diene, like compound 12, for example, there is a choice of where it will react, with either of the C=C double bonds. Compound 12 was modelled, and the geometry optimised, taking into account electronic effects within the diene using a Mopac model, and the resulting geometry was compared with that produced by only the MM2 model.
The difference in geometry was small, but noticeable. When overlaying the resulting models, keeping the bridgehead and bridging carbons in the same places, as well as one on the outer edge,the difference in the position of the Chlorine was measured to be 0.3 Angstroms, as were the carbon atoms in the unfixed diene - on the side closer to the Hydrogen on the bridging Carbon, and further from the Cl atoms themselves. Thus the electronic interactions clearly make a difference to the geometry.
In order to attempt to predict the outcome of a reaction with an electrophile, 4 of the frontier orbitals and the overall electron density were both calculated:
|
|
|
|
| |||||||||||||||
| MO 47: HOMO - 1 | MO 48: HOMO | MO 49: LUMO | MO 50: LUMO + 1 | Electron density | |||||||||||||||
| Surfaces modelled using Gaussian DFT method, 6-31G basis set | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
As it reacts as a nucleophile, initially donating electrons to the incoming electrophile, it makes sense to observe the HOMO, the most likely orbital for those electrons to come from, as this will have the greatest stabilizing effect on the molecule. In this case, the HOMO clearly shows electrons localised to one side of the molecule - the C=C double bond nearest the Cl atom. This is supported by the overall electron density - There is more negative regions (blue) above and below this double bond than the other, so the electrophile will be more attracted to this side of the molecule in the first place.
In fact, it is reported that it is possible to attribute this directing effect toward the one C=C bond, as well as the above geometrical effect, primarily to a favourable interaction between the π-bonding orbitals and the σ* orbitals on the Chlorine atom,[4] as clearly shown by the model HOMO, which bears a close spatial similarity to those orbitals.
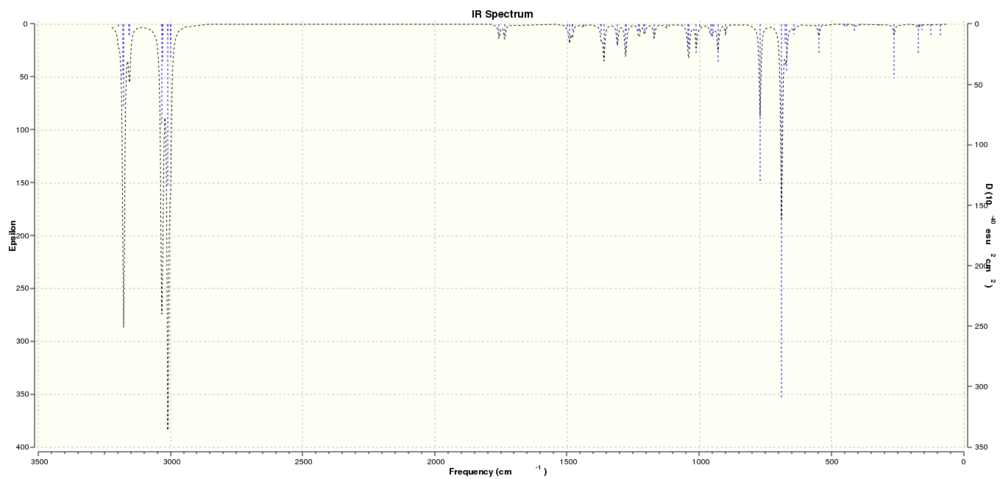
In order to find further differences, and supply evidence for this deduction, the IR spectrum was predicted from the molecule using Gaussian, and the vibrational frequencies used to infer relative bond energies.
IR Spectrum
The interpretation of the IR implies that the C=C bond closer to the Cl is slightly higher in vibrational energy, and this suports its reactivity when comaperd to the C=C on the other side of the molecule. This fits its known reactivity, and shows the effectiveness of models that include MO theory factors.[4][5]
Monosaccharide Glycosidation

A vital step in the formation of glycosides, and carbohydrates, is the glycosidation reaction. In many syntheses, Acetyl groups are useful in controlling the selectivity of the reaction, due to the anomeric effect.[6] This stereochemistry originates from the intermediates shown. These intermediates were modelled, and the configurations of the shown red Acetyl group varied, as were - independently - the configurations of that group with respect to the anomeric carbon, in order to inverstigate the relative stability of the geometries. The energy of each geometrical arrangement was minimised using first an MM2 method, then Mopac, in order to estimate relative stability. The results are shown for intermediates A and B.
Results
| Compound | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
|
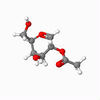
|

|
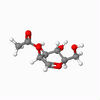
| |
| Details | S enantiomer, "down" conformer | S enantiomer, "up" conformer | R enantiomer, "down" conformer | R enantiomer, "up" conformer |
| MM2 Energy / kcal mol-1 |
19.7359 | 10.9370 | 4.1300 | 7.1777 |
| Mopac Energy / kcal mol-1 |
-77.6159 | -87.9516 | -80.2174 | -71.5680 |
| Compound | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
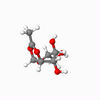
|
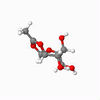
|
|
| |
| Details | S enantiomer, "down" conformer | S enantiomer, "up" conformer | R enantiomer, "down" conformer | R enantiomer, "up" conformer |
| MM2 Energy / kcal mol-1 |
13.5140 | 23.8073 | 18.4622 | 26.1293 |
| Mopac Energy / kcal mol-1 |
-98.2356 | -111.3171 | -112.3205 | -100.2097 |
Thus it is clear that, on cyclisation of the acetyl group, arrangement 1 is strongly favoured, meaning that the reaction is likely to follow this to the predicted result, matching literature expectations.[7]
Part 3: Mini-project

| |||
| Compound 17 Geometry |
The Calculations and models discussed thus far were used to produce predictions for the geometry and spectroscopy for 2 molecules:
Taxol intermediate
The first molecule was Compound 17: another intermediate in the Taxol synthesis. The geometry was optimised and the 1H and 13C NMR spectra predicted.
1H NMR
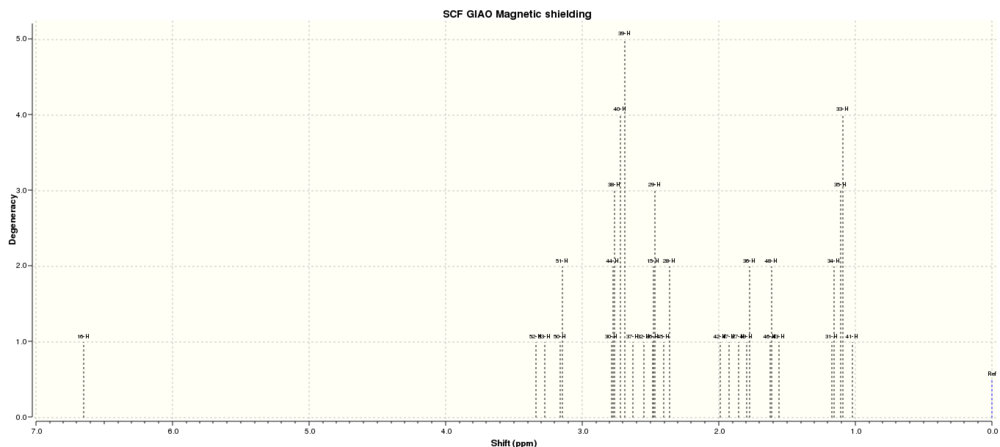
|
| 1H NMR Spectrum predicted by Gaussian (Solvent = Water, Reference = TMS) |
|---|
13C NMR

|
| 13C NMR Spectrum predicted by Gaussian (Solvent = Water, Reference = TMS) |
|---|
Comparing these spectra to those found in the literature,[8] the 1H NMR spectrum is noticeably different, while the 13C spectrum is nearly identical. While it is tempting to assign this discrepancy to the calculation method, in fact the literaature spectra were recorded in CDCl3, not water, and it makes sense that the 1H spectrum is affected more by a change to a protic solvent.
Literature molecule

| |||
| Compound 4 Geometry |
The molecule selected from the literature for spectroscopic analysis and prediction is Compound 4, an intermediate in the synthesis of Caffeine,[9] chosen because the range of heteroatoms provide several interesting NMR environments, and IR stretches.
1H NMR
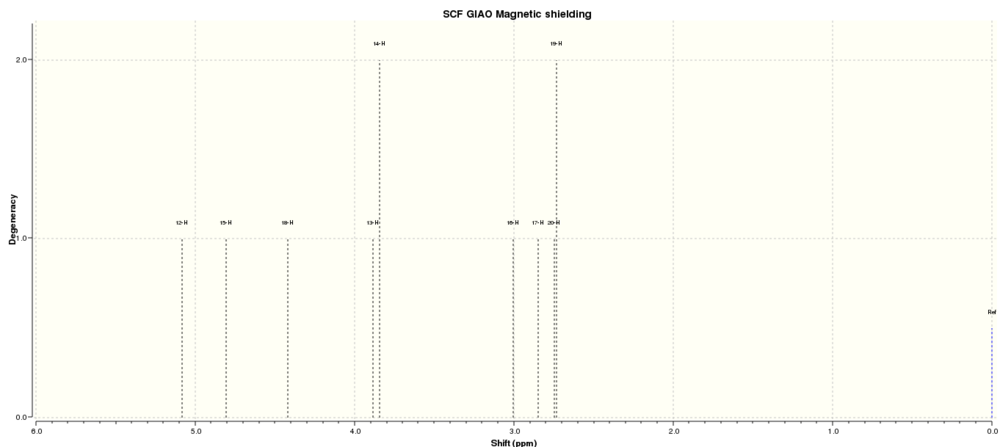
|
| 1H NMR Spectrum predicted by Gaussian (Solvent = DMSO (deuterated), Reference = TMS) |
|---|
13C NMR
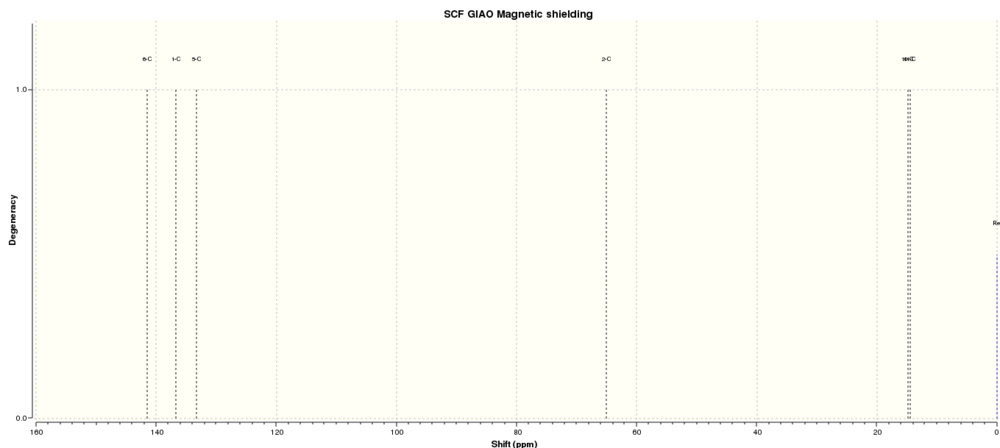
|
| 13C NMR Spectrum predicted by Gaussian (Solvent = DMSO (deuterated), Reference = TMS) |
|---|
Comparing these spectra to literature compounds,[10], it can be seen that they are very similar, even if, in the 1H spectra especially, the calculated spectra has a tendency to separate the peaks far more than in the experimental spectrum.
IR
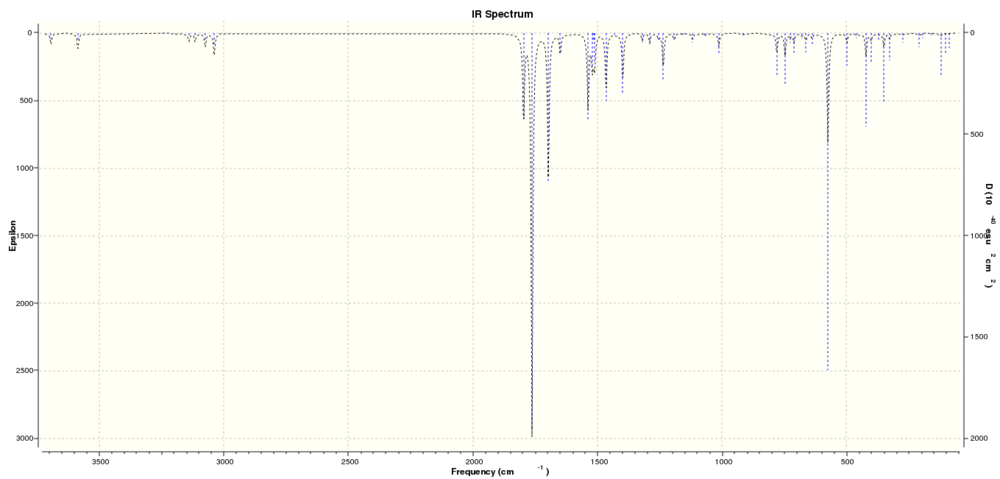
|
| IR Spectrum predicted by Gaussian |
|---|
The IR spectrum has much better correlation to literature results.[10] which implies that the DFT method used by Gaussian to generate these models may be more accurate at reproducing the vibrational stretches and frquencies than calculating the environments and shielding of nuclei in a simulated NMR experiment.
References
- ↑ P. Caramella, P. Quadrelli and L. Toma, J. Am. Chem. Soc., 2002, 124 (7), 1130–1131 DOI:10.1021/ja016622h
- ↑ 2.0 2.1 P. Atkins and J. De Paula, Atkins' Physical Chemistry, Oxford University Press, Oxford, 2006
- ↑ J. G. Vinter and H. M. R. Hoffmann, J. Am. Chem. Soc., 1974, 96 (17), 5466-5478 DOI:10.1021/ja0082a025
- ↑ 4.0 4.1 Brian Halton and Sarah G. G. Russell, J. Org. Chem., 1991, 56 (19), pp 5553–5556 DOI:10.1021/jo00019a015
- ↑ B. Halton, R. Boese and H. S. Rzepa, J. Chem. Soc., Perkin Trans 2, 1992, 4, 447-448. DOI:10.1039/P29920000447
- ↑ Laurel K. Mydock and Alexei V. Demchenko, Org. Biomol. Chem., 2010, 8, 497-510
- ↑ Dennis M. Whitfield and Tomoo Nukada, Carbohydr. Res., 2007, 342, 1291 DOI:10.1016/j.carres.2007.03.030
- ↑ Leo A. Paquette, Neil A. Pegg, Dana Toops, George D. Maynard and Robin D. Rogers, J. Am. Chem. Soc., 1990, 112, 277-283 DOI:10.1021/ja00157a043
- ↑ Matthew A. Zajaca, Anthony G. Zakrzewskia, Mark G. Kowala and Saraswathi Narayan, Synthetic Commun., 2003, 33 (19), 3291-3297 DOI:10.1081/SCC-120023986
- ↑ 10.0 10.1 S. V. Shorshnev, S. E. Esipov, A. I. Chernyshev, A. F. Pozharskii, V. V. Kuz'menko and A. V. Gulevskaya, Chem. Heterocycl. Compd., 1990, 26 (2), 191-200 DOI:10.1007/BF00499415