Jack Rogan - Module 2

Week 1 - Using Gaussian

BH₃ Optimisation

B3LYP Basis set

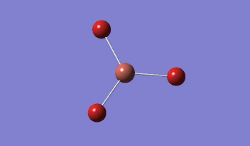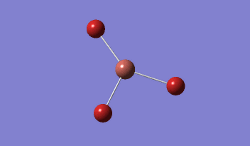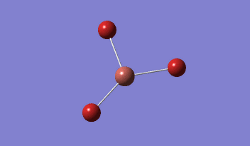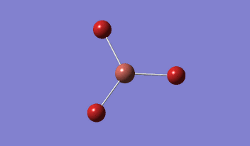
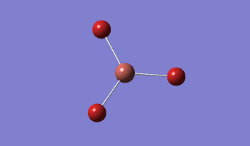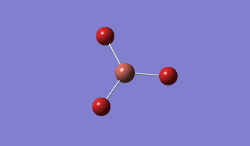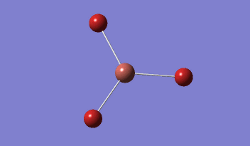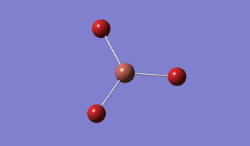
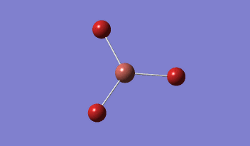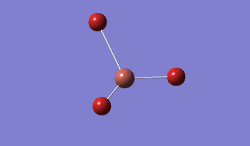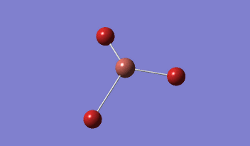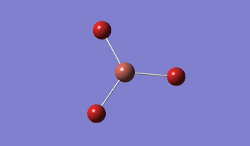
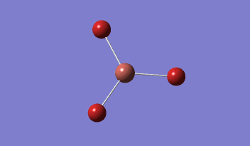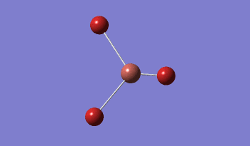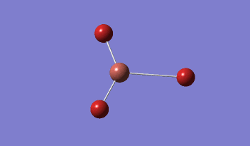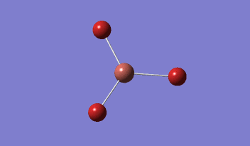
BH₃ was modelled, and optimised, first, with a B3LYP method and 3-21G basis set.

Geometry
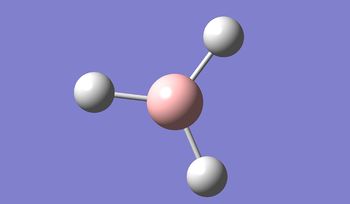
B-H Bond Distance / Å	1.19
H-B-H Bond angle / °	120.0

Summary
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	3-21G
Final Energy / au	-26.462
Gradient / au	0.000
Dipole Moment / D	0.00
Point Group	D_3H
Calculation Time / min:sec	1:54

Output

         Item               Value     Threshold  Converged?
 Maximum Force            0.000413     0.000450     YES
 RMS     Force            0.000271     0.000300     YES
 Maximum Displacement     0.001610     0.001800     YES
 RMS     Displacement     0.001054     0.001200     YES
 Predicted change in Energy=-1.071764D-06
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,2)                  1.1935         -DE/DX =    0.0004              !
 ! R2    R(1,3)                  1.1935         -DE/DX =    0.0004              !
 ! R3    R(1,4)                  1.1935         -DE/DX =    0.0004              !
 ! A1    A(2,1,3)              120.0            -DE/DX =    0.0                 !
 ! A2    A(2,1,4)              120.0            -DE/DX =    0.0                 !
 ! A3    A(3,1,4)              120.0            -DE/DX =    0.0                 !
 ! D1    D(2,1,4,3)            180.0            -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------
 GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

6-31G(d,p) Basis set

The geometry was further optimised using the same method, but a more accurate - and calculation-intensive - 6-31G basis set instead.

Result: JR_BH3_OPTIMISATION_2

Geometry
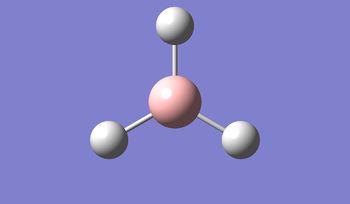
B-H Bond Distance / Å	1.19
H-B-H Bond angle / °	120.0

Summary
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Final Energy / au	-26.615
Gradient / au	0.000
Dipole Moment / D	0.00
Point Group	C_S
Calculation Time / min:sec	0:07 (On HPC)

Output

         Item               Value     Threshold  Converged?
 Maximum Force            0.000005     0.000450     YES
 RMS     Force            0.000003     0.000300     YES
 Maximum Displacement     0.000020     0.001800     YES
 RMS     Displacement     0.000012     0.001200     YES
 Predicted change in Energy=-1.312911D-10
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,2)                  1.1923         -DE/DX =    0.0                 !
 ! R2    R(1,3)                  1.1923         -DE/DX =    0.0                 !
 ! R3    R(1,4)                  1.1923         -DE/DX =    0.0                 !
 ! A1    A(2,1,3)              120.0002         -DE/DX =    0.0                 !
 ! A2    A(2,1,4)              120.0002         -DE/DX =    0.0                 !
 ! A3    A(3,1,4)              119.9997         -DE/DX =    0.0                 !
 ! D1    D(2,1,4,3)            180.0            -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------
 GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

Pseudo-potentials

TlBr₃

For TlBr_s, the symmetry was constrained to the D3H point group, and the energy and geometry optimised, this time using a LanL2DZ basis set - using pseudo-potentials to model non-valence orbitals on atoms on the second row of the periodic table or below. The Calculation was performed on the HPC.

Result:

Published to DSpace: DOI:10042/21133
.log File: JR_TLBR3OPTIMISATION

Geometry
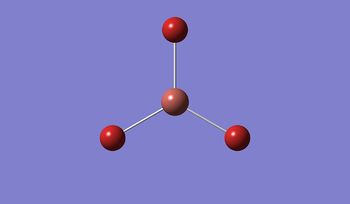
Tl-Br Bond Distance / Å	2.65
Br-Tl-Br Bond angle / °	120.0

Summary
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	LANL2DZ
Final Energy / au	-91.218
Gradient / au	0.000
Dipole Moment / D	0.00
Point Group	D_3H
Calculation Time / min:sec	0:38 (On HPC)

         Item               Value     Threshold  Converged?
 Maximum Force            0.000002     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000022     0.001800     YES
 RMS     Displacement     0.000014     0.001200     YES
 Predicted change in Energy=-6.084022D-11
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,2)                  2.651          -DE/DX =    0.0                 !
 ! R2    R(1,3)                  2.651          -DE/DX =    0.0                 !
 ! R3    R(1,4)                  2.651          -DE/DX =    0.0                 !
 ! A1    A(2,1,3)              120.0            -DE/DX =    0.0                 !
 ! A2    A(2,1,4)              120.0            -DE/DX =    0.0                 !
 ! A3    A(3,1,4)              120.0            -DE/DX =    0.0                 !
 ! D1    D(2,1,4,3)            180.0            -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------
 GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

This bond length was compared to literature values to verify that the calculation had completed without serious errors: literature reports a bond length of 2.55 Å,^[1] which, when compared to the calculated result of 2.65 Å, is only a 4% difference, and is therefore plausible.

BBr₃

In BBr₃, the combination of larger, comre complicated atoms, and smaller, simpler ones led to optimising the molecule by specifying that the Br atoms should be modelled using a pseudo-potential-based LanLDZ basis, and the B using 6-31G(d,p).

Result: JR_BBR3OPTIMISATION

Geometry
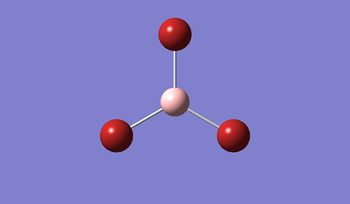
B-Br Bond Distance / Å	1.93
Br-B-Br Bond angle / °	120.0

Summary
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	Gen
Final Energy / au	-64.436
Gradient / au	0.000
Dipole Moment / D	0.00
Point Group	D_3H
Calculation Time / min:sec	2:05

         Item               Value     Threshold  Converged?
 Maximum Force            0.000008     0.000450     YES
 RMS     Force            0.000005     0.000300     YES
 Maximum Displacement     0.000036     0.001800     YES
 RMS     Displacement     0.000023     0.001200     YES
 Predicted change in Energy=-4.027020D-10
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,2)                  1.934          -DE/DX =    0.0                 !
 ! R2    R(1,3)                  1.934          -DE/DX =    0.0                 !
 ! R3    R(1,4)                  1.934          -DE/DX =    0.0                 !
 ! A1    A(2,1,3)              120.0            -DE/DX =    0.0                 !
 ! A2    A(2,1,4)              120.0            -DE/DX =    0.0                 !
 ! A3    A(3,1,4)              120.0            -DE/DX =    0.0                 !
 ! D1    D(2,1,4,3)            180.0            -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------
 GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

Results & Bonding analysis

Table of optimised bond differences
Molecule	BH₃	BBr₃	TlBr₃
Bond Length / Å	1.19	1.93	2.65

It is clear that, in this case, the replacement of a Hydrogen substituent with a Bromine ligand results in a longer bond distance, by 0.74 Å, and the replacement of the central Boron with Thallium similarly lengthens the bond - by 0.72 Å. This implies that both the nature of the ligand and of the centre make a difference to the bond nature and strength - and therefore length.

Firstly, the nature of the Hydrogen atom can be compared to that of a Bromine atom - with respect to a Boron centre. Hydrogen is very small, and electron-deficient compared to Bromine. This is likely to result in a much more covalent bond with the Boron centre, as they are similar in electronegativity (Pauling electromnegativities: 2.0 and 2.2 for B and H respectively)^[2] and therefore the individual bonds will have very little polarisation. Bromine, on the other hand, is slightly higher in electonegativity (2.9)^[2], which will polarise the bond slightly more, lending it ionic character and lengthening it. However, a greater contribution to the longer bond is likely to be the size of the Br orbitals - as Br has 3 filled shells, giving much larger and more diffuse orbitals compared to those of Hydrogen - which has no filled shells, possessing only one electron. In addition, there will be the interaction of the non-bonding Br p_z orbitals with the unfilled B p_z orbital, leading to some electron donation from the Br, and a bond which, in fact, possesses some π-character, and is therefore longer. This will lead to the empty p_z orbitals on the Boron being less available to electron donation, and the BBr₃ molecule slightly more stable to lewis bases than the difference in bond length would suggest.

As far as the central atoms are concerned, this data implies a that the Thallium centre will make a shorter bond to the ligand than a Boron, all other things being equal. Boron and Thallium are in the same group, and therefore the same number of electrons are shared with, in this case, Bromine. However, as Thallium much lower down the group, it is bonded very differently. This time, Bromine is much more electronegative than Thallium (1.6)^[2], and the bond much more polarised. Leaving the bond closer to being ionic. In addition, the Thallium orbitals, given its position in the periodic table, are much more diffuse and larger than bromine, so the bond is longer and weaker anyway. In addition, the quasi-π interaction with the bromine is gone completely, due to the complete mismatch in size and energy of the p_z orbitals on both atoms. Thus the B-Br bond is both shorter and stronger than Tl-Br.

In some cases, Gaussview does not show bonds where, logically,they should be expected. This is because it uses a purely geometrical view of bonds, showing "bond" lines on the model only where the distances are within an expected "bond length" set of distances. This in no way informs that a bond is not present.

Bonds are the effect of overlapping orbitals and of several different forms of electron transfer and sharing. An atom is said to be bonded to another when the distance between them corresponds to an energy minimum from electronic effects. As such, the lengths of them are very variable, and even atoms at what would be considered "extreme" distances share electron density in some manner, and thus can be said to be bonding. However, the limits are not an arbitrary bond/not-bond line - special cases like, for example, Hydrogen-bonding, are not normally shown when drawing a molecule, but they involve electronic attraction between atoms, and make a considerable effect on the geometry and energy of their molecules.

Frequency Analysis

BH₃

A frequency, or vibrational analysis was calculated for the 6-31G(d,p)-optimised BH₃ molecule.

Result: JR_BH3_OPT_FREQ

Geometry
B-H Bond Distance / Å	1.19
H-B-H Bond angle / °	120.0

Summary
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Final Energy / au	-26.615
Gradient / au	0.000
Dipole Moment / D	0.00
Point Group	C_2V
Calculation Time / min:sec	2:39

Output

 Item               Value     Threshold  Converged?
 Maximum Force            0.000005     0.000450     YES
 RMS     Force            0.000002     0.000300     YES
 Maximum Displacement     0.000020     0.001800     YES
 RMS     Displacement     0.000009     0.001200     YES
 Predicted change in Energy=-1.329322D-10
 Optimization completed.
    -- Stationary point found.
 GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

 Low frequencies ---  -18.6669   -0.0009   -0.0003    0.0006   12.5167   12.5631
 Low frequencies --- 1162.9785 1213.1756 1213.2363

Vibration Summary

Summary of vibrations acting on BH₃
#	Vibration Form	Frequency / cm^-1	Intensity	Symmetry (Molecule: D_3H)
1		1163	93	A₂'
1	All B-H bonds stretching symmetrically, all atoms moving up and down z-axis	1163	93	A₂'
2		1213	14	E'
2	One B-H unit vibrating in x direction, with slight bond vibration, other H atoms rotating symmetrically around z-axis (through x-y plane)	1213	14	E'
3		1213	14	E'
3	One BH₂ unit rotating around z-axis (through x-y plane), other H vibrating in y-axis, asymmetrically stretching B-H bond.	1213	14	E'
4		2582	0	A₁'
4	All B-H bonds stretching symmetrically out in the x-y plane. B atom is still.	2582	0	A₁'
5		2715	126	E"
5	2 B-H bonds stretch out from B atom - opposite motion to each other, other H atom remains still, while B atom oscillates in y axis	2715	126	E"
6		2715	126	E"
6	All B-H bonds stretching - 1 in opposite phase to the other 2, B atom oscillates in x direction	2715	126	E"

IR Spectrum

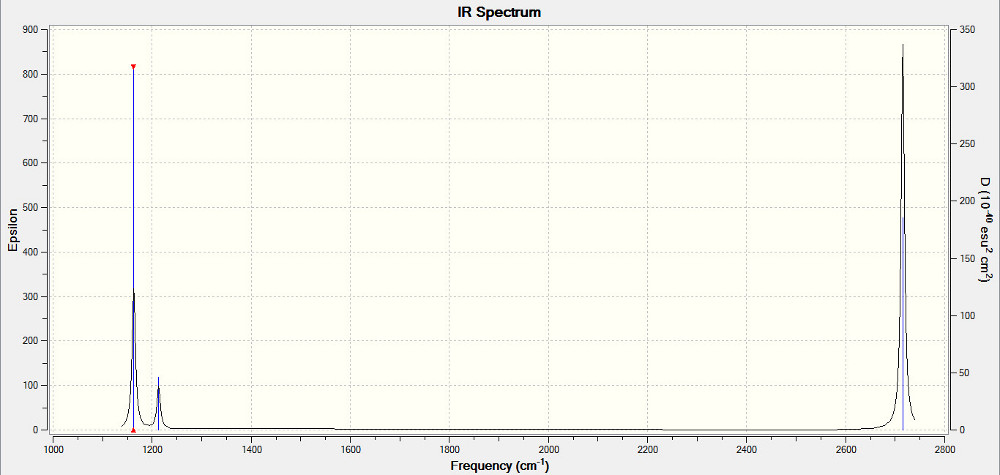
IR Spectrum for BH₃

While there are clearly 6 vibrations for BH₃, there are only 3 peaks in the IR spectrum. This is because, of those vibrations, there are 2 sets of 2 degenerate vibrations, which contribute to the same peak, not forming separate ones at diffrerent frequencies. In addition, one of the vibrations - the A₁' symmetrical stretch, has 0 intensity. It is not IR active because there is no change to the overall dipole moment.

TlBr₃

A similar frequency analysis was carried out on TlBr₃

Result:

Published to DSpace: DOI:10042/21176
.log File: JR_TLBR3_OPT_FREQ

Geometry
Tl-Br Bond Distance / Å	2.65
Br-Tl-Br Bond angle / °	120.0

Summary
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	LANL2DZ
Final Energy / au	-91.218
Gradient / au	0.000
Dipole Moment / D	0.00
Point Group	D_3H
Calculation Time / min:sec	0:31 (On HPC)

Output

         Item               Value     Threshold  Converged?
 Maximum Force            0.000002     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000022     0.001800     YES
 RMS     Displacement     0.000011     0.001200     YES
 Predicted change in Energy=-5.660901D-11
 Optimization completed.
    -- Stationary point found.
 GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

 Low frequencies ---   -3.4213   -0.0026   -0.0004    0.0015    3.9367    3.9367
 Low frequencies ---   46.4289   46.4292   52.1449

Vibration Summary

Summary of vibrations acting on TlBr₃
#	Vibration Form	Frequency / cm^-1	Intensity	Symmetry (Molecule: D_3H)
1		46	4	E'
1	One Tl-Br unit vibrating in x direction, with slight bond vibration, other Br atoms rotating symmetrically around z-axis (through x-y plane)	46	4	E'
3		46	4	E'
3	One TlBr₂ unit rotating around z-axis (through x-y plane), other Br vibrating in y-axis, asymmetrically stretching Tl-Br bond.	46	4	E'
2		52	6	A₂'
2	All Tl-Br bonds stretching symmetrically, all atoms moving up and down z-axis	52	6	A₂'
4		165	0	A₁'
4	All Tl-Br bonds stretching symmetrically out in the x-y plane. Tl atom is still.	165	0	A₁'
5		211	25	E"
5	2 Tl-Br bonds stretch out from Tl atom - opposite motion to each other, other Br atom remains still, while Tl atom oscillates in y axis	211	25	E"
6		211	25	E"
6	All Tl-Br bonds stretching - 1 in opposite phase to the other 2, Tl atom oscillates in x direction	211	25	E"

IR Spectrum

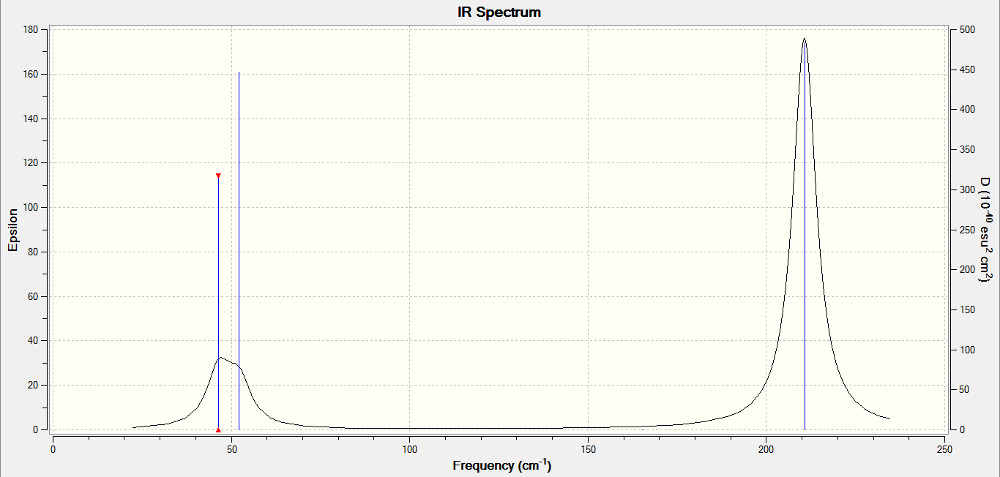
IR Spectrum for TlBr₃

Comparison of Vibrational Frequencies

Comparison of Vibrational Frequencies
Vibration Symmetry	BH₃		TlBr₃
Vibration Symmetry	Wavenumber / cm^-1	Intensity	Wavenumber / cm^-1	Intensity
A₁'	2582	0	165	0
A₂'	1163	93	52	6
E'	1213	14	46	4
E'	1213	14	46	4
E"	1275	126	211	25
E"	1275	126	211	25

The frequencies for BH₃ and TlBr₃ are very different, with those for BH<aub>3 being much higher. This corresponds to much heavier Tl and Br atoms, which therefore vibrate at much lower frequencies.In addition, the vibrational modes themselves are in a different order, in terms of frequency and energy; given that the molecules have the same D_3H symmetry, it makes sense that the vibrational modes would be the same.

However, in both spectra, 2 groups of vibrational modes are predicted, the lower-energy A₂' and E' modes, and the higher-energy A₁' and E" modes. In TlBr₃, the order of the higher-energy group is reversed, with the E" modes higher in energy, while, for the lower-energy group, they are all so close together as to not be readily distinguishable on a printed spectrum, and certainly not when calculation error is taken into account. This is most likely because, given the heavier Br atom mass, the deformation into less symmetrical geometries will require more energy than the symmetrical deformations.

It is important to use the same basis set and method for both the optimisation and frequency calculations because the energy values are highly dependent on the method used, and, in fact, cannot be compared at all to those generated by other methods and basis sets, thus, if a frequency analysis is run from an energy corresponding to a different method or basis set, the program will start from a completely different place in its analysis, and therefore the result is extremely likely to be both very different, and highly inaccurate. A frequency analysis both confirms that the optimisation has reached an energy minimum, and gives us the opportunity to predict vibrational modes and therefore the IR spectrum, without handling the actual molecule.

The low frequencies represent the -6 modes in the 3N-6 vibrational modes of a molecule (for which N is the number of atoms). These are the modes corresponding to the centre of mass of the molecule vibrating.

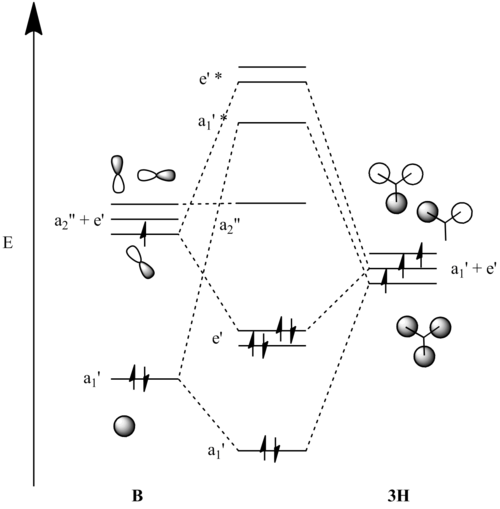
Orbital Analysis

BH₃ MOs

A population analysis of the Molecular Orbitals of BH₃ was run.

Results: JR_BH3_MOS

Geometry
B-H Bond Distance / Å	1.19
H-B-H Bond angle / °	120.0

Summary
File Type	.log
Calculation Type	SP
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Final Energy / au	-26.615
Gradient / au	0.000
Dipole Moment / D	0.00
Point Group	C_2V
Calculation Time / min:sec	1:38

MOs for BH₃
MO diagram	MO Symmetry	Drawn MO	Calculated MO
	e' *
	e' *
	a₁' *
	a₂"
	e'
	e'
	a₁'

Clearly, the predicted orbitals bear a reasonable resemblance to the calculated MOS, but the calculations provide a much more accurate picture.

NH₃ Optimisation / Frequency

A molecule of NH₃ was modelled, optimised and a frequency analysis used to verify that a minimum had been reached, using a B3LYP method and 6-31G(d,p) basis set.

Result: JR_NH3OPTIMISATION

Geometry
N-H Bond Distance / Å	1.02
H-N-H Bond angle / °	105.7

Summary
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Final Energy / au	-56.558
Gradient / au	0.000
Dipole Moment / D	1.85
Point Group	C₁
Calculation Time / min:sec	5:54

Output

         Item               Value     Threshold  Converged?
 Maximum Force            0.000024     0.000450     YES
 RMS     Force            0.000012     0.000300     YES
 Maximum Displacement     0.000079     0.001800     YES
 RMS     Displacement     0.000053     0.001200     YES
 Predicted change in Energy=-1.629727D-09
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,2)                  1.018          -DE/DX =    0.0                 !
 ! R2    R(1,3)                  1.018          -DE/DX =    0.0                 !
 ! R3    R(1,4)                  1.018          -DE/DX =    0.0                 !
 ! A1    A(2,1,3)              105.7413         -DE/DX =    0.0                 !
 ! A2    A(2,1,4)              105.7486         -DE/DX =    0.0                 !
 ! A3    A(3,1,4)              105.7479         -DE/DX =    0.0                 !
 ! D1    D(2,1,4,3)           -111.8631         -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------
 GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

Frequency analysis: JR_NH3FREQUENCY

Geometry
N-H Bond Distance / Å	1.02
H-N-H Bond angle / °	105.7

Summary
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Final Energy / au	-56.558
Gradient / au	0.000
Dipole Moment / D	1.85
Point Group	C₁
Calculation Time / min:sec	3:03

Output

         Item               Value     Threshold  Converged?
 Maximum Force            0.000021     0.000450     YES
 RMS     Force            0.000009     0.000300     YES
 Maximum Displacement     0.000078     0.001800     YES
 RMS     Displacement     0.000039     0.001200     YES
 Predicted change in Energy=-1.611689D-09
 Optimization completed.
    -- Stationary point found.
 GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
<pre>
 Low frequencies ---  -30.7295   -0.0018   -0.0014   -0.0012   20.1705   28.2664
 Low frequencies --- 1089.5535 1694.1244 1694.1856

NH₃ NBOs

NBO Charge Distribution

Range	-1.125 - 1.125
Specific NBO Charge (N)	-1.125
Specific NBO Charge (H)	0.375

Association Energy

A molecule of NH₃BH₃ was optimised using B3LYP/6-31G(d,p).

Result: JR_NH3BH3OPTIMISATION

Summary
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Final Energy / au	-82.767
Gradient / au	0.000
Dipole Moment / D	5.8431
Point Group	C₁
Calculation Time / min:sec	4:48

Output

         Item               Value     Threshold  Converged?
 Maximum Force            0.000086     0.000450     YES
 RMS     Force            0.000032     0.000300     YES
 Maximum Displacement     0.000356     0.001800     YES
 RMS     Displacement     0.000192     0.001200     YES
 Predicted change in Energy=-5.461725D-08
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,8)                  1.0277         -DE/DX =   -0.0001              !
 ! R2    R(2,8)                  1.0277         -DE/DX =   -0.0001              !
 ! R3    R(3,8)                  1.0277         -DE/DX =   -0.0001              !
 ! R4    R(4,7)                  1.212          -DE/DX =   -0.0001              !
 ! R5    R(5,7)                  1.212          -DE/DX =   -0.0001              !
 ! R6    R(6,7)                  1.212          -DE/DX =   -0.0001              !
 ! R7    R(7,8)                  1.6854         -DE/DX =   -0.0001              !
 ! A1    A(4,7,5)              113.5634         -DE/DX =    0.0                 !
 ! A2    A(4,7,6)              113.5634         -DE/DX =    0.0                 !
 ! A3    A(4,7,8)              104.99           -DE/DX =    0.0                 !
 ! A4    A(5,7,6)              113.555          -DE/DX =    0.0                 !
 ! A5    A(5,7,8)              104.9821         -DE/DX =    0.0                 !
 ! A6    A(6,7,8)              104.982          -DE/DX =    0.0                 !
 ! A7    A(1,8,2)              109.3494         -DE/DX =    0.0                 !
 ! A8    A(1,8,3)              109.3494         -DE/DX =    0.0                 !
 ! A9    A(1,8,7)              109.5868         -DE/DX =    0.0                 !
 ! A10   A(2,8,3)              109.347          -DE/DX =    0.0                 !
 ! A11   A(2,8,7)              109.5969         -DE/DX =    0.0                 !
 ! A12   A(3,8,7)              109.5969         -DE/DX =    0.0                 !
 ! D1    D(4,7,8,1)            179.9996         -DE/DX =    0.0                 !
 ! D2    D(4,7,8,2)            -60.0015         -DE/DX =    0.0                 !
 ! D3    D(4,7,8,3)             60.0006         -DE/DX =    0.0                 !
 ! D4    D(5,7,8,1)            -59.996          -DE/DX =    0.0                 !
 ! D5    D(5,7,8,2)             60.0029         -DE/DX =    0.0                 !
 ! D6    D(5,7,8,3)           -179.9949         -DE/DX =    0.0                 !
 ! D7    D(6,7,8,1)             59.9952         -DE/DX =    0.0                 !
 ! D8    D(6,7,8,2)            179.9941         -DE/DX =    0.0                 !
 ! D9    D(6,7,8,3)            -60.0038         -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------
 GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

Frequency analysis: JR_NH3BH3FREQUENCY

Summary
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Final Energy / au	-83.225
Gradient / au	0.000
Dipole Moment / D	5.56
Point Group	C₁
Calculation Time / min:sec	0:44

Output

        Item               Value     Threshold  Converged?
 Maximum Force            0.000264     0.000450     YES
 RMS     Force            0.000058     0.000300     YES
 Maximum Displacement     0.001470     0.001800     YES
 RMS     Displacement     0.000376     0.001200     YES
 Predicted change in Energy=-2.149033D-07
 Optimization completed.
    -- Stationary point found.
 GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

 Low frequencies ---   -8.8787   -0.0008   -0.0005    0.0013   19.3581   19.5894
 Low frequencies ---  263.3197  631.2464  638.5704

Comparison of Energies
Molecule	Final Energy / au
BH₃	-26.615
NH₃	-56.558
NH₃BH₃	-83.225
ΔE	0.052
ΔE / kJ mol^-1	137

Project: Lewis Acids and Bases

The Calculations required to optimise, carry out a frequency analysis, and view the MOs (of the least energetic) of 4 isomers of Al₂Cl₄Br₂ were run on the HPC, and published to DSpace.

Result:

Isomer 1

Optimisation: DOI:10042/21414
Frequency: DOI:10042/21418
MOs: DOI:10042/21423

Isomer 2

Optimisation: DOI:10042/21415
Frequency: DOI:10042/21419

Isomer 3

Optimisation: DOI:10042/21416
Frequency: DOI:10042/21421

Isomer 4

Optimisation: DOI:10042/21417
Frequency: DOI:10042/21420

References

↑ M. Atanasov and D. Reinen, J. Phys. Chem. A, 2001, 105 (22), pp 5450–5467 DOI:10.1021/jp004511j
↑ ^2.0 ^2.1 ^2.2 P. Atkins and J. De Paula, Atkins' Physical Chemistry, Oxford University Press, Oxford, 2006

[AR2001-1] M. Atanasov and D. Reinen, J. Phys. Chem. A, 2001, 105 (22), pp 5450–5467 DOI:10.1021/jp004511j

[ATKINS-2] 2.0 ^2.1 ^2.2 P. Atkins and J. De Paula, Atkins' Physical Chemistry, Oxford University Press, Oxford, 2006

[1]

[2]

Jack Rogan - Module 2

Week 1 - Using Gaussian

BH3 Optimisation

B3LYP Basis set

6-31G(d,p) Basis set

Pseudo-potentials

TlBr3

BBr3

Results & Bonding analysis

Frequency Analysis

BH3

Vibration Summary

IR Spectrum

TlBr3

Vibration Summary

IR Spectrum

Comparison of Vibrational Frequencies

Orbital Analysis

BH3 MOs

NH3 Optimisation / Frequency

NH3 NBOs

Association Energy

Project: Lewis Acids and Bases

References

BH₃ Optimisation

TlBr₃

BBr₃

BH₃

TlBr₃

BH₃ MOs

NH₃ Optimisation / Frequency

NH₃ NBOs