Rep:Mod:JPS1123
Synthesis and computational lab: 1C James Simpson (CID:00733493)
A computational experiment investigating the properties of aysmmetric epoxidation of different olefins using the Shi and Jacobsen epoxidations.
Introduction
Chemistry
Diels-Alder Reaction
The Diels-Alder reaction is one of the most famous examples of a cyclo-addition, it was discovered by Otto Diels and Kurt Alder[1]. It is the addition of a conjugated diene and an alkene and proceeds via a Hückel topology[2] with suprafacial components[3],[4]. As the reaction requires heat the electron count is 2n+2, 4 π electrons come from the conjugated diene and 2 π electrons from the alkene, so there are 6 π electrons involved in the reaction. When the diene and alkene have substituents the reaction has two products; the exo and endo products. The difference in these two products is due to the difference in the transition states. For the endo product to form then in the transition state the diene's substituents must face towards the π system of the diene. However in the case of the exo product the opposite is true. Below the stereochemistry of the two different products of a Diels-Alder reaction can be compared: the reaction in this case is that of cis-butadiene and maleic anhydride.
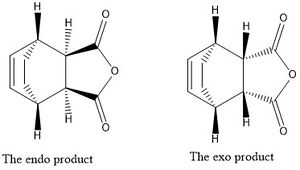
It is also possible that a diene will form a dimer with itself as the result of a Diels-Alder cyclo-addition. It is known that 1,3-cyclohexadiene can self dimerize[5],reductively in ammonia[6]. Indeed 1,3-butadiene, which reacts in the prototype, will dimerize with itself and can, under certain conditions, polymerize as can 1,3-cyclopentadiene.
Epoxidation
Epoxides are a class of compounds in which a 3-ringed cyclic ether exists. These ethers are more reactive than standard ethers due to the steric strain caused by the three membered ring system. Of course, the carbons on the three membered ring are sp3 hybridized and so can exhibit chirality - this led research to make possible the asymmetric epoxidation, which was first done in 1980 by Katsuki and Sharpless[7]. Examples of asymmetric epoxidation catalysts include the Jacobsen catalyst and a catalyst derived from D-fructose for use in the Shi epoxidation. These two reactions will be looked at in detail in this experiment.
Computational Programmes and Methods
ChemBio3D
ChemBio3D is a piece of software which allows the user to view a drawn molecule in 3D. It is mostly used for biological molecules. The program allows for structure clean-up and for calculations to be used in order to calculate NMR IR and mass spectra as well as minimisations.
Gaussian
Gaussian is a computational chemistry program; the latest version is G09. In order to speed up computational time gaussian-like orbitals are used instead of Slater-type orbitals. The program can be used for many different calculations, including density functional theory. The program can also be used to view NMR and other calculated data such as optical rotation.
MMFF94
Merck Molecular Force Field are force fields based on the MM3 force field and the earliest force field in this family is MMFF94. The calculations used by this method are solely iterative methods until a local minima is reached, when the method is used to optimize a structure. The method is designed in order to work for a large range of molecules.
DFT
Density Functional Theory is a computational method that calculates the properties of a molecule using the electronic structure of that system - the ground state is usually used. In this method the properties are found by functions of other functions, in this case the spatially dependent electron density.
Part 1
Conformational Analysis Using Molecular Mechanics
Dimerization of Cyclopentadiene
| Exo | Endo | |||||
|---|---|---|---|---|---|---|
| Structure | ||||||
| Energy kcalmol-1 | 55.3731 | 58.1928 |
It is well known that 1,3-cyclopentadiene can dimerize by undergoing a Diels-Alder reaction with itself. It is also known that the endo product is the major product formed[8] and from this it is possible to calculate whether or not the reaction is thermodynamically or kinetically controlled. This can be easily and quickly done using ChemBio3D and calculating the energy of the optimized endo and exo products using MMFF94 and determining which is lower in energy. From Table 1 (right) it can be seen that the exo product has an energy of 55.3731 kcalmol-1 compared to an energy of 58.1928 kcalmol-1 for the endo product. This shows that the exo product of the Diels-Alder dimerization of cyclopentadiene is the thermodynamically stable product and this means that if the reaction was under thermodynamic control then in fact the exo product would be the major product. However it is known that the endo product is the major product of the reaction and thus the reaction must be under kinetic control. This means that the transition state of the endo product must be lower in energy that the transition state of the exo product due to secondary orbital interactions stabilizing the transition structure of the endo pathway.
Partial Hydrogenation of Cyclopentadiene

Of course the product of the dimerization of cyclopentadiene can be reacted further, and one interesting reaction is the partial hydrogenation of the dimer i.e. the hydrogenation of only one of the remaining C=C bonds. It is clear to see, from above, that if a hydrogenation occurs there are two sites that can be hydrogenated and these sites have for ease been named double bond 1 and double bond 2. These are shown above and in order to calculate which product is most likely formed if the reaction is controlled thermodynamically, the thermodynamic product, the energies of the two possible products, can found from the optimized products. This along with other data was calculated using MMFF94 and MM2 in ChemBio3D and the results of these calculations are shown below in Table 2:
| Bond Hydrogenated | Double Bond 1 | Double Bond 2 | ||||
|---|---|---|---|---|---|---|
| Structure | ||||||
| Energy kcal-1 (From MMFF94) | 50.7262 | 41.2617 | ||||
| Energy kcal-1 (From MM2) | 35.9266 | 31.1521 | ||||
| Stretching | 1.2358 | 1.0962 | ||||
| Bending | 18.9382 | 14.5283 | ||||
| Stretch-Bend | -0.7608 | -0.5491 | ||||
| Torsion | 12.1249 | 12.4976 | ||||
| Non-1,4 Van der Waals | -1.5027 | -1.0734 | ||||
| 1,4 Van der Waals | 5.7282 | 4.5119 | ||||
| Electrostatic Energy | 0.1631 | 0.1406 |
From the data shown in the table it is obvious that when the reaction is under thermodynamic control then the double bond 2 will be hydrogenated preferably to double bond 1. This is because the energy of product of hydrogenation on the second double bond is 41.2617 kcal-1, compared to the energy of the product of hydrogenation on the first double bond, which is 50.7262. It is also noticeable that the stretching of the hydrogenation product of the second double bond is lower than the first as is the bending and Van der Waals, both 1,4 and non-1,4. It is possible that the result of the hydrogenation would be different if the reaction was under kinetic control and this can be considered due to sterics. As double bond 2 is more easily and therefore more quickly hydrogenated[9], is it clear that, in this particular case when hydrogenation occurs, double bond 2 will be hydrogenated no matter if the reaction occurs under thermodynamic or kinetic control, as the hydrogenated product arising from hydrogenation of the second double bond will be the major product in either case.
Atropisomerism in an Intermediate Related to the Synthesis of Taxol
| Molecule 9 | Molecule 10 | |||||||
| Optimized boat |
|
| ||||||
| Optimized twist-boat |
|
|
Paclitaxel, sold as Taxol, is a drug used in chemotherapy for many types of cancer as it inhibits mitosis. Molecules 9 and 10, shown below, are products of intermediate steps in the synthesis of taxol[10] and as can be seen from Table 3 the difference in these conformers is the position of the oxygen atom in the carbonyl group: in molecule 9 it is pointing 'up' relative to the 'down' configuration of molecule 10. However it is found that a mixture of both isomers leads to a single isomer. This observation is explained by the fact that the addition of the carbonyl group in this synthesis is under thermodynamic control; it must be reversible for this effect to be seen and hence the isomer that is formed is the one lowest in energy. This will be the more stable isomer and so the lowest energy structures of both isomers were found and the energies were found by using MMFF94. The two lowest energy chair conformers are shown below along with some another minimum, in this case a local minimum of a twist-boat conformer not the global minimum of the chair conformer shown.
The high energy conformers shown indicate one of the different conformers that molecule 10 can adopt. This was done by changing the conformer of the cyclohexane ring within the molecule, which is possible due to ring flipping that will be occurring. From Table 3 above it is obvious that under thermodynamic control, which the reaction must be, that molecule 10 is lower in energy (60.5445 kcalmol-1) than molecule 9 (60.6329 kcalmol-1) and so molecule 9 will, over time, convert into molecule 10. However this conversion happens slowly because of the double bond located at the bridgehead of the main ring and the bridge[11]. According to Bredt's rule, in smaller ring systems the C-C double bond will not be found at the bridgehead[12] as this would effectively create a trans double bond in the ring system and lead to an unstable strain on the system. However in this system, as the ring is quite large, the double bond actually increases the stability of the system as the ring strain of the ring containing the double bond is less than the ring strain without the double bond. This leads to a much lower reactivity of the system as the unsaturated system is more stable than the saturated system, leading to the slow conversion rate from molecule 9 to molecule 10 that is observed.
Spectroscopic Simulation using Quantum Mechanics
Naturally, of course, there are other molecules that are used in the synthesis of Taxol[10]; two of these molecules are 17 and 18. Both of these molecules can have NMR spectroscopy simulated on them and the results of the NMR can be compared to literature[13]; the literature values will be reported along with the simulated NMR. It is only necessary for one of the molecules, either 17 or 18, to have the NMR simulated as the chemical shifts will be very similar for both of them and in this case molecule 17 was chosen as it was the first of those two molecules to be made. These calculations were done using B3LYP theory and the 6-31G(d,p) basis set with the solvent being set, in this case, as chloroform as this is the solvent used in literature. The calculation was then sent to the High Performance Computer (HPC) in order to save time.
H1 NMR
| 3D Representation | 2D Representation | H1 NMR | C13 NMR | ||
|---|---|---|---|---|---|
NMR |
 |
 |
| Atom Number | Simulated Chemical Shift ppm | Atom Number | Simulated Chemical Shift ppm |
|---|---|---|---|
| 24 | 5.0579 | 44 | 2.023 |
| 53 | 3.3320 | 23 | 2.0188 |
| 26 | 3.2395 | 18 | 2.0058 |
| 52 | 3.1518 | 22 | 1.997 |
| 50 | 3.1450 | 20 | 1.8766 |
| 51 | 3.0956 | 25 | 1.7178 |
| 34 | 2.7945 | 45 | 1.7023 |
| 19 | 2.7658 | 27 | 1.6842 |
| 21 | 2.755 | 46 | 1.6068 |
| 15 | 2.5947 | 30 | 1.5360 |
| 33 | 2.5337 | 43 | 1.3373 |
| 31 | 2.3017 | 47 | 1.2097 |
| 42 | 2.2696 | 29 | 1.1567 |
| 41 | 2.1436 | 32 | 1.1225 |
| 17 | 2.0307 | 28 | 0.8232 |
| Chemical Shift pp | Multiplicity | |
|---|---|---|
| 5.21 (Multiplet) | 1 H | |
| 3.00-2.70 (Multiplet) | 6 | |
| 2.70-2.35 (Multiplet) | 4 | |
| 2.20-1.70 (Multiplet) | 6 | |
| 1.58 (Triplet, J = 5.4 Hz) | 1 | |
| 1.50-1.20 (Multiplet) | 3 | |
| 1.10 (Singlet) | 3 | |
| 1.07 (Singlet) | 3 | |
| 1.03 (Singlet) |
Using MMFF94 when optimizing the initial structure of molecule 18 gave the energy to be 96.9768 kcal/mol. It should be noted that the atoms in the molecule have been given tags and this made it possible to see the exact chemical environments for each atom (the atomic tags can be seen from either the 2D representation or the 3D representation by hovering over the atom about which more information is required). The results of the NMR can be seen from the tables below or from the internet[14]. The free energy of the system was found to be -1651.464393 Hartree. Not much could be gained from the comparison of the simulated spectra and literature H1 NMR spectra of molecule 17, shown in Tables 5 and 6, because of the lack of coupling in the simulated system, whereas obviously the literature spectrum contained coupling between hydrogen atoms on the same carbon, if they were not in the same chemical environment, and the hydrogen atoms on neighboring carbons. Another effect that could not be seen in the simulated spectrum was coupling of the peaks that would occur in real NMR spectra. In the simulated spectra the peaks were also infinitely thin, like Dirac delta functions, and an effect of this was that there was no overlap of peak as would be seen in reality: this could be seen because there were fewer separate peaks in the literature spectrum than there were in the computational spectrum that was computed. This was why, instead of the 30 peaks seen for the literature spectrum, there were only 9 peaks seen as lots of the peaks were overlapping.
C13 NMR
| Atom Number | Simulated Chemical Shift | Literature Chemical Shift | Deviation |
|---|---|---|---|
| 11 | 206.4126 | 211.49 | 5.0774 |
| 4 | 133.5372 | 148.72 | 15.1828 |
| 5 | 117.3664 | 120.90 | 3.5336 |
| 35 | 81.5341 | 74.61 | -6.9241 |
| 12 | 51.8568 | 60.53 | 8.6732 |
| 13 | 47.7891 | 51.30 | 3.5109 |
| 3 | 42.6316 | 50.94 | 8.3084 |
| 7 | 39.1093 | 45.53 | 6.4207 |
| 38 | 38.7812 | 43.28 | 4.4988 |
| 49 | 35.9164 | 40.82 | 4.9036 |
| 48 | 34.5782 | 38.73 | 4.1518 |
| 36 | 31.2418 | 36.78 | 5.5382 |
| 6 | 30.2704 | 35.47 | 5.1996 |
| 1 | 26.4138 | 30.84 | 4.4262 |
| 10 | 21.6320 | 30.00 | 8.368 |
| 8 | 19.5445 | 25.56 | 6.0155 |
| 2 | 16.5036 | 25.35 | 8.8464 |
| 37 | 15.1032 | 22.21 | 7.1068 |
| 9 | 15.0420 | 21.39 | 6.348 |
| 16 | 9.6447 | 19.83 | 10.1853 |
It was clear that the carbon NMR was much more useful than the hydrogen NMR: this was because the carbon NMR contained no splitting or broadening of peaks, which could lead to overlap. Therefore it is entirely possible to compare the computationally calculated NMR with a literature reference of an experiment; the comparison of these NMRs can be seen in Table 7. The calculated results compared well with what was expected i.e. the chemical shift of carbon 11, which is a ketone at 206.4126ppm: this was within the typical range for a ketone environment, which is around 200ppm. Carbons 4 and 5 also had chemical shifts in the expected range for a C=C bond, which was in the area of 150-120ppm for the values of the chemical shift. The actual values for the chemical shifts were 133.5372ppm for carbon 4 and 117.3664ppm for carbon 5. The reason for the relatively large difference in the shift values was due to the slightly different environments. The carbon with a higher shift is 4: this was as expected as typically more substituted C=C bonds display higher chemical shifts. When comparing the calculated NMR and the literature it was obvious that there were some differences in the values of the chemical shifts - in order to make this clearer the difference in the values is shown in the column on the right and it should be noted that the mean value of the deviation was 5.968555ppm with a standard deviation of 3.99933ppm. These differences were due to the computational method, which of course was not perfect. However the deviation will also have been affected by the fact that the molecule for which the NMR was calculated was molecule 17, while the molecule for which the literature NMR was obtained was molecule 18. The difference between these two molecules was the same as the difference between molecules 9 and 10. However the effect that changing the position of the C=O bond would have had on the NMR would have been small and so the major reason for the difference is the computational method itself.
Part 2
For the second part of this experiment both Shi and Jacobsen asymmetric epoxidation will be simulated on a choice of four molecules; Styrene, β-methylstyrene, trans-Stilbene and 1,2-dihydronaphthalene. The two molecules that have had aysmmetric epoxidations simulated on them are styrene and trans-stilbene: the differences of these reactions will be discussed in the course of the exercise.
The two Catalytic Systems
Shi Fructose-Derived Catalyst
| Atoms | Bond Length | Atoms | Bond Length | Atoms | Bond Length |
|---|---|---|---|---|---|
| C12-O1 | 1.437 | C8-O4 | 1.427 | C14-O5 | 1.433 |
| C12-O3 | 1.435 | C8-O2 | 1.424 | C14-O4 | 1.434 |
A precursor in the synthesis of the catalyst of the Shi aysmmetric epoxidation was found. This precursor was stable and the actual catalyst in the Shi epoxidation was generated from this precursor and persulfuric acid. The mechanism used to make the catalyst was an adaptation[15] of the synthetic route first used by Shi[16]. It would be expected from looking at the C-O bond lengths at the anomeric centres of the molecule, of which there are three, that there would be an anomeric effect occurring where there was electron donation from the p orbital of the oxygen atom into the π* orbital of the C-O bond occurring on the other oxygen atom. For this to occur the oxygens must be gauche relative to each other, and in this case they were. It could be seen that on each anomeric centre that one of the carbon oxygen bonds was longer than the other carbon oxygen bond in the anomeric centre (see Table 8). This was because the oxygen atoms were in slightly different chemical environments, which results in different pKa values for the different conjugate alcohol, and this results in one bond becoming longer than the other C-O bond[17}.
Jacobsen Catalyst
The catalyst used in the Jacobsen aysmmetric epoxidation is shown below. One of the ways that it can be synthesized was proposed by Hansen[18] , who adapted it from the original synthesis made by Jacobson[19-20]. The particular catalyst has been used in the synthesis of Taxol since 1992[21]. The structure of the precatalyst was found using the program ConQuest and this species can be made into the activated catalyst that does the epoxidation by adding NaOCl.
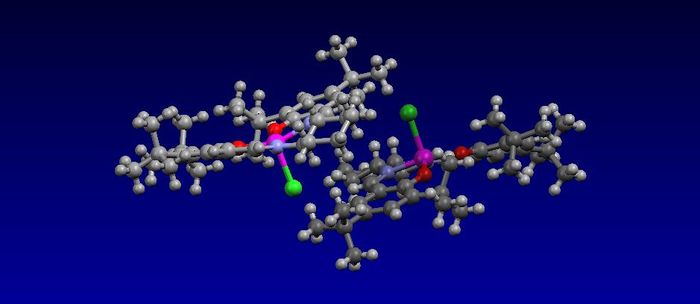
From the structure of the precursor Jacobson catalyst there was one thing that stood out more than anything else and that was that attack of the Mn atom could only occur on either the top or bottom face of the molecule. The molecule is largely planar and protected in this plane by the multiple ring systems that link together, and therefore protect, the majority of that plane from attack at the Mn atom. The ring system does not cover the whole plane but this is not an issue due to the large tert-Butyl groups present that will protect the rest of that plane. This means that attack can only occur on either the top or bottom face and this is what was observed experimentally[19-20].
The calculated NMR properties of your products
Styrene Oxide
| R/RR | S/SS | |||||
|---|---|---|---|---|---|---|
| Styrene | ||||||
| Silbene |
It was stated earlier that the two epoxidations that would be computationally carried out were those of styrene and trans-silbene in chloroform, as this would allow them to be easily compared to literature. Epoxidations in both cases would lead to two possible chiral products, and it was likely that the Shi aysmmetric epoxidation and the Jacobsen aysmmetric epoxidation would each give different products in each case. These products would, of course, be enantiomers of each other. The structures of the four possible products are shown to the left in Table 9. In order to check that the structure of the epoxide products were correct it was necessary to run an NMR simulation of the products. The results of these calculations can be seen in Tables 10 and 11 for styrene, and Tables 12 and 13 for trans-stilbene. It should be noted that in order to see which atom corresponds to which environment the 2D representation at the top of each column should be viewed as the numbers after the H in brackets are the atomic tags of the hydrogens atoms attached to that carbon. The data for these NMRs can be accessed online[22-25].
The first set of molecules that will be considered are the epoxides formed from the epoxidation of styrene. From inspection of Table 9 it is clear that the products had the same simulated NMR spectra for both H1 NMR and C13 NMR. The spectra also showed that all but two carbons were seen to be aromatic and those that were not were normal shifts for carbons in an epoxide ring, as was expected. The same was true with the hydrogen atoms except that there were now three hydrogen atoms that were not aromatic, two bonded to carbon 13 or 8 and one bonded to carbon 12 or 7, depending on which enantiomer was being considered. It was expected that the carbon which was higher shift was the one closer, directly bonded to, the aromatic ring and this was seen to be the case, as can be seen from the data on Figure 10, as the R enantiomer for the chemical shift for carbon 7 was found to be 44.3447ppm and the shift for carbon 8 was found to be 43.7515ppm. For the S enantiomer the chemical shift for carbon 12 was 44.3506ppm, while the chemical shift for carbon 13 was found to be 43.7225ppm. The same should be true for hydrogens so for the R enantiomer hydrogens 16 and 17 should be lower in chemical shift than hydrogen 15. This was found to be the same, as the chemical shifts for hydrogens 16 and 17 were 2.6701ppm and 3.2502ppm respectively while for hydrogen 15 the chemical shift was 3.7997ppm. For the S enantiomer the same should also be true in that hydrogen 15 should have a higher chemical shift than both of the hydrogens 16 and 17. This was also the case, as the chemical shift for hydrogen 15 was 3.8011ppm while the chemical shifts for hydrogens 16 and 17 were 2.6665ppm and 3.2472ppm respectively.
| R enantiomer | S enantiomer | ||
|---|---|---|---|
| H1 NMR |  |
 | |
| C13 NMR |  |
 |
Stilbene Oxide
| RR enantiomer | SS enantiomer | ||
|---|---|---|---|
| H1 NMR |  |
 | |
| C13 NMR |  |
 |
If the spectra of the epoxides formed from trans-stilbene are considered it is clear from looking at the data on Table 12 that the products all have the same simulated NMR spectra for both H1 NMR and C13 NMR. The spectra also show the expected peaks for such a product as all but two carbons are seen to be aromatic and those that are not are normal shifts for carbons in an epoxide ring. The same is true if the hydrogen atoms are considered. As the molecule is symmetrical in chemical terms there will be no real difference in the chemical shifts for either of the aromatic rings, or indeed for the non aromatic carbons found in the epoxide ring.
Assigning the absolute configuration of the product
It is possible to determine the direction that each enantiomer rotates in polarized light and this can be done computationally. A B3LYP DFT calculation was run on the HPC, the solvent used was cholorform between 589nm and 365nm, and this gave the following results: R-stryene oxide was calculated to have an optical rotation of -30.11o, while the S enantiomer was calculated to have an optical rotation of 30.11o ; RR-stilbene oxide was calculated to have an optical rotation of 297.91o and the other enantiomer, SS-stilbene oxide, was calculated to have an optical rotation of -297.91o. Along with this the Vibrational Circular Dichroism (VCD) spectrum of all four of these molecules were calculated and these are shown in Table 13. VCD is a useful spectroscopic technique which gives 3D structural information of molecules by detecting differences in polarized light passing through a sample. It is an extension of circular dichroism spectroscopy, where the wavelengths of light used are increased into the IR and UV spectra, and is mainly used for complex proteins and DNA. It was clear that the VCD spectra for each epoxiation product was the reflection of its enantiomer, which was consistent with the enantiomers being correctly found. The spectra and data can be accessed online on Imperial College DSpace[26-29].
The values of the computational calculated optical rotations were then compared to literature; R-styrene oxide was calculated to have an optical rotation value of -30.11o; this compared with a literature value in chloroform of -23.7o[30]. The literature result in this case showed that the direction in which light was computed to have rotated was the same as the direction in which it actually rotated. However the value of the rotation was about 20% different to the actual value, although the actual difference was small due to the nature of the computation method. The S-styrene oxide's calculated optical rotation value was also compared to literature; different sources gave different results ranging from 32.1o[31] to 25.1o[32-33] and these literature values also agree with the calculated optical rotation value for S-styrene oxide, which was found to be 23.7o. From these results it is clear that both the R-styrene oxide and S-styrene oxide agree quite with literature, as although these values were not precisely the same as the literature values they did show that the light was rotated in the expected direction, which suggested that the computation had been rather successful. For the R,R-stilbene oxide the calculated optical rotation was found to be 297.91o, compared to literature values of 250.8o[34] and 239.2o[35]. The other enantiomer of stilbene oxide also had its literature values for optical rotation data in chloroform; these literatures were -249o[36] and -320o[36] compared to the calculated value of -297.91o. Once again, just as for styrene oxide, the values were not exactly the same as the literature values but the light had been rotated in the same direction as expected. It is thus now possible to state that R-epoxystyrene is (-)styrene oxide and S-styrene oxide is (+)styrene oxide. It is also possible to state that RR-stilbene oxide is (+)stilbene oxide and that SS-stilbene oxide is (-)stilbene oxide.
Another possible technique that could have been used is ECD or electronic circular dichroism but as this requires multiple chromophores for the spectrum to be of any use, and as none of the epoxides have a chromophore, doing this calculation using this technique would have been completely pointless and therefore the technique has not been used in this experiment.
Using the (pre-calculated) Properties of Transition State for the Reaction
 |
The next part of this experiment involved deciding which product was formed from each of the four epoxidations i.e. styrene and trans-stilbene epoxidation using both the Shi and Jacobsen asymmetric epoxidation. This was done by finding the pre-calculated energy of the given transition states in case, provided by Rzepa[38-45],[47-50],[52-59],[60-61] and deciding which was the lowest in energy and therefore the one that would occur. Of course the products in each in case would be the same and it must be the energy of the transition states that determines whether the R/RR or S/SS enantiomer is formed in each case. The number of given transition states for the Shi asymmetric epoxidation was four for all the possible products. However for the Jacobsen asymmetric epoxidation only two possible transition states were provided for the stryene oxides and for the stilbene oxide only one transition state was provided. Once the correct transition state has been found for both the R/RR and S/SS enantiomer the free energy of the particular should be found, also provided by Rzepa[38-59]. Obviously the transition state with the lower free energy will be the more stable transition state and therefore the enantiomer that will be formed from this transition state will be the major product. The free energies of the transition states can be visualized in the diagram to the right. The difference in this free energy can be used in order to determine the enantiomeric excess using the equations:
Styrene Oxide Shi Epoxidation
| Transition State 1 |
|
Transition State 2 |
| ||||||
| Transition State 3 |
|
Transition State 4 |
|
The first enantiomer that was considered was the R-styrene oxide made using the Shi asymmetric epoxidation. The energies of the four possible candidates were found from the data provided[38-41], shown in Table 14. It is clear from the table that the transition state with the lowest energy was in fact transition state 4. This means that if R-styrene oxide is being formed as the product of the Shi asymmetric epoxidation then the reaction will go through transition state 4 as the transition state of the reaction. From this the Gibbs free energy of the found transition state can be determined: this was listed in the thermochemistry section of the file for the forth transition state[41] as the sum of electronic and thermal free energies and was found to be -1303.738503 Hartree. However, this number on its own is practically useless and so to do anything meaningful the transition state and the Gibbs free energy of the transition state for S-styrene oxide must be found.
| Transition State 1 |
|
Transition State 2 |
| ||||||
| Transition State 3 |
|
Transition State 4 |
|
For the possible transition states that will lead to the S-styrene enantiomer the data[42-45] was accessed in order to find the energies of the possible transition states. The results are found in Table 15 and once again it can be seen that the lowest energy transition state with an energy of -1304.12329360 Hartree was transition state 4. Therefore, as for the R-styrene oxide, in order to form S-styrene using the Shi asymmetric epoxidation the reaction must proceed through transition state 4. After this was done the Gibbs free energy was found from the data files[45] in the thermochemistry section as the sum of electronic and thermal free energies, and was -1303.738044 Hartree. Now that the energies of both transition states for both enantiomers of styrene oxide have been found it can be stated that the major product will be the S-styrene oxide enantiomer as it is lower by 0.000459 Hartree or 1.1934kJmol-1. From this K was found to be 1.618358 and the enantiomeric excess was found to be 23.62%. This means that 61.81% of the total product using the Shi aysmmetric epoxidation will be the S while 38.19% while be the R enantiomer. However, comparison with literature values gives the enantiomeric excess as 13.6% with the R-styrene oxide being the major product[46], showing that the major product calculated in this experiment is actually the minor product. There are a number of reasons why this result might have occurred, the most likely being that the lowest energy transition state found for the R-styrene enantiomer is not, in fact, the lowest transition state. Whether or not this is true is not known because, as stated before, the calculation required to optimize to a transition state takes too long to do in the time frame of the experiment. Of course, if a lower energy transition state for the R-styrene enantiomer were to be found then it would favour the formation of the R enantiomer and therefore make it the major product.
Styrene Oxide Jacobsen Epoxidation
| Transition State 1 (R enantiomer) |
|
Transition State 2 (R enantiomer) |
| ||||||
| Transition State 1 (S enantiomer) |
|
Transition State 2 (S enantiomer) |
|
Now that the major product of the Shi asymmetric epoxidation has been calculated, despite it giving the wrong enantiomer as the major product, the Jacobsen asymmetric epoxidation should be investigated to see which enantiomer of styrene oxide is the major product and the enantiomeric excess of the reaction. If the R-styrene oxide enantiomer is being made then, using the data provided by Rzepa[47-48], transition state 2 will be the transition state of the epoxidation, with an energy of -3344.62638393 Hartree. This was found to be lower in energy than transition state 1, with an energy of -3344.62471803 Hartree, as can be seen from Table 16. The free energy of this transition state was then found to be -3343.962162 Hartree using the data provided by Rzepa[48]. This energy was the sum of electronic and thermal free energies within the thermochemistry section of the data file. However, if the S-styrene oxide enantiomer is being made then the reaction will follow the reaction path containing transition state 1 as this transition state was lower in energy, from data provided by Rzepa[49-50], than the path with transition state 2 as the maximum, as can be seen from Table 16.
Again the sum of electronic and thermal free energies could be found from data, in the thermochemistry section. This energy was -3343.969197 Hartree and by comparing the free energies of the lowest energy transition state for each enantiomer of styrene being formed, it is clear that the major product of this reaction is the S-styrene oxide enantiomer as the transition state is lower in energy by 0.007035 Hartree, which is 18.291 kJmol-1. Using the formulae above it is calculated that the value of K in this case is therefore 1601.197. From this the value of the enantiomeric excess can be found, which was done using the equation at the beginning of this section and found to be 99.8752%. This means that 99.94% of the product formed will be S-styrene oxide, while only 0.06% of the product formed will be the R enantiomer. It was seen for the Shi epoxidation that the results did not compare at all well to literature, as the wrong major product was found. However for the Jacobsen epoxidation the literature found stated that the major product was in fact R-styrene with an enantiomeric excess with a 57% enantiomeric excess[51]. The possible reason for this difference is again that the global minimum for the transition state of the R-enantiomer was not in fact found but due to the time constraints of the experiment a optimization to a Berny transition state is not possible.
Stilbene Oxide Shi Epoxidation
| Transition State 1 |
|
Transition State 2 |
| ||||||
| Transition State 3 |
|
Transition State 4 |
|
| Transition State 1 |
|
Transition State 2 |
| ||||||
| Transition State 3 |
|
Transition State 4 |
|
The absolute configuration of the products of the epoxidation of styrene using both the Shi and Jacobsen asymmetric epoxidation was calculated in the previous section and these results were then compared to literature. The same process was done with the epoxidation of trans-stilbene, starting with the Shi epoxidation, using data provided by Rzepa[52-55]. It was clear from looking at Table 17 that the lowest energy transition state of the given transition states was transition state 3, which had an energy of -1535.16270178 Hartree. From the data of the file containing information about the structure and energy of transition state 3, the Gibbs free energy of the system could be found under thermochemistry as the sum of electronic and thermal free energies. This energy was found to be -1534.700037 Hartree. However, before any sense can be made of this free energy value, the free energy of the lowest energy transition state for the production of SS-stilbene oxide must be found.
This was done using data provided by Rzepa[56-59] and it is clear from the energies shown in Table 17 that the lowest energy transition state of the transition states given was transition state 3 with an energy of -1535.15629511 Hartree. The data within this transition state could then be used in order to find the sum of electronic and thermal free energies, the Gibbs free energy, which was found was to be -1534.693818 Hartree. The difference of free energies of the lowest energy transition state for the epoxidation of both products was found to be 0.006219 Hartree, 16.1694 kJmol-1. The free energy of the RR-stilbene oxide transition state was lower than the free energy of the SS-stilbene oxide and from this the value of K was calculated to be 680.3878 and the enantiomeric excess was found to be 99.7065%. This means that 99.85% of the product made will be the RR enantiomer of stilbene oxide while only 0.15% will be the SS enantiomer. A literature value for this particular epoxidation was an enantiomeric excess of 95.2% with the major product being RR-stilbene oxide[46]. Unlike the cases of styrene oxide, this fits quite well with literature as the correct major product has been found. However there were some discrepancies in the enantiomeric excess and this could be due to there being a lower energy transition state for the SS-stilbene oxide pathway, i.e. a local minimum in the transition state energy was found and not the global minimum.
Stilbene Oxide Jacobsen Epoxidation
| RR enantiomer Formed |
|
SS enantiomer Formed |
|
In the case of the Jacobsen asymmetric epoxidation of trans-stilbene there was only one transition state supplied[60-61] and so it was not necessary to compare the different energies of the transition states, only the free energy of the two transition states. These are as follows: the sum of electronic and thermal free energies for the RR enantiomer being formed is -3574.921174 Hartree while for the SS enantiomer being formed the sum of electronic and thermal free energies was found to be -3574.923087 Hartree. The energy difference therefore is 0.001913 Hartree (4.9738 kJmol-1) with the transition state for the SS enantiomer being the major product of the reaction. This energy difference was used to find the value of the equilibrium constant to be 7.43656 and hence the enantiomeric excess was calculated to be 76.29%. This means that 88.15% of the product in the Jacobsen asymmetric epoxidation will be SS-stilbene oxide and 11.85% will the RR-stilbene oxide. Again these results were compared to literature: these showed the major product to be SS-stilbene oxide with an enantiomeric excess of 33%. Once again the literature finds the same major product as the computational method, but with a large difference in the enantiomeric excess. The reason for this difference has been stated previously. The results of the four epoxidations can be summarized below:
| Jacobsen Epoxidation | Shi Epoxidation | |||||||
|---|---|---|---|---|---|---|---|---|
| Styrene |
|
| ||||||
| Trans-Stilbene |
|
|
It should be noted that the epoxidations of styrene using both the Shi and Jacobsen epoxidation methods completely disagreed with literature results obtained from experiment and that while the Jacobsen epoxidation of trans-stilbene gave the same major as literature, the enantiomeric excess obtained from the computational files disagreed with the enantiomeric excess obtained from experiment.
Investigating the non-covalent interactions in the active-site of the reaction transition state
Non-covalent interactions (NCI) are any interaction within a molecule that are not bonding interactions. This interactions include hydrogen bonds, electrostatic attractions and Van der Waals interactions. These interactions are visualized using NCI analysis where the color shown shows the attractiveness or repulsiveness of the interaction (blue is attractive, green mildly attractive, yellow mildly repulsive and red repulsive). NCI analysis was undertaken of one of the transition states seen earlier and in this case the transition state was transition state 3 for the Shi epoxidation of trans-stilbene leading to the formation of RR-stilbene oxide.
|
It is clear that the vast majority of these interactions are the mildly attractive Van der Waals interactions between atoms. However, one interesting interaction is the interaction between one of the oxygen atoms in the dioxirane ring and the two carbons in the C=C bond not part of an aromatic ring. This interaction is strongly attractive as would be expected because the interaction is the partial formation of two bonds, one from each carbon in the olefin to the oxygen atom in the dioxirane ring.
Investigating the Electronic topology (QTAIM) in the active-site of the reaction transition state
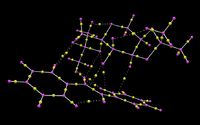
The Quantum Theory of Atoms in Molecules is another technique that can be used to investigate the non-bonding interactions in the transition structure. The technique can be used alongside NCI analysis as the electron density is the important part of this technique. This is done by identifying bond critical points (BCP), which is where the non-bonding interactions are strongest. Mathematically this is done by taking the derivative of the electron density in all three spatial coordinates. The transition state structure that has been analysed with this method is transition structure 3 of the Shi epoxidation of trans-stilbene leading to the formation of RR-stilbene oxide. The QTAIM of this transition state can be found below.

Suggesting new candidates for investigations

There are other olefins that are interesting to study: the criteria for a candidate for study should be that it rotates polarized light more than 300o, as this makes it easier to calculate the rotation accurately, and it should also have a molecular weight less than 200. From a search of reaxys a possibly interesting olefin to conduct an epoxidation on is (2E)-3-[(1R,5S)-5-Vinyl-2-cyclopenten-1-yl]-2-propen-1-ol, the structure of which is shown to the right. The molecule was chosen as its optical rotation is 304.6o in CH2Cl2 at 549nm[62} and its molecular mass is below 200. It is clear that the molecule can be easily made from simple reterosynthetic steps, including Wittig reactions. The presence of mulitple C=C bonds will lead to the possibility of different epoxide products arising. So the preferred position of epoxide formation can be investigated with different catalysts in order to help understand the nature of both catalysts used in the Shi and Jacobsen epoxidation
References
1. O.P.H. Diels, K. Alder, Liebigs Ann., 1928, 460, 98-122
2. H. Rzepa's Teaching e-materials, http://www.ch.ic.ac.uk/rzepa/, (accessed 8-19 Dec)
3. R.B. Woodward, R. Hoffmann, J. Am. Chem. Soc., 1965, 87, 2511
4. R. Hoffman, K. Fukui, J. Am. Chem. Soc., 1967, 87, 395
5. R.T. Sanderson, Science., 1952, 116, 41-42
6. Y. Li, K.N. Houk, J. Am. Chem. Soc., 1993, 115, 7478-7485
7. T. Katsuki, K.B. Sharpless, J. Am. Chem. Soc., 1980, 102, 5974-5976
8. Imperial College Chemistry Wiki, https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:organic, (accessed 8-19 Dec)
9. D. Skála, J. Hanika, Petroleum and Coal, 2003, 45, 105-108
10. S.W. Elmore, L. Paquette, Tetrahedron Lett., 1991, 319
11. W.F. Maier, P. Von Rague Schleyer, J. Am. Chem. Soc., 1981, 103, 1891
12. J. Bredt, Liebigs Ann., 1924, 437,1-13
13. L. Paquette, N.A. Pegg, D. Toops, G.D. Maynard, R.D. Rogers, J. Am. Chem. Soc., 1990, 112, 277-283.
14. J.P. Simpson, (2014), Imperial Spectra DSpace, DOI:10042/147286 Taxol 17 NMR Data
15. A. Burke, P. Dillon, K. Martin, T.W. Hanks, J. Chem. Educ., 2000, 77, 271
16. O.A. Wong, B. Wang, M-X Zhao, Y. Shi, J. Org. Chem., 2009, 74, 335-6338
17. A.J. Briggs, R. Glenn, P.G. Jones, A.J. Kirby, P. Ramaswamy, J. Am. Chem. Soc., 1984, 106 , 6200-6206
18. J. Hanson, J. Chem. Educ., 2001, 78, 1266
19. E.N. Jacobsen, W. Zhang, A.R. Muci, J.R. Ecker, L. Deng, J. Am. Chem. Soc., 1991, 113, 7063-7064
20. M. Palucki, N.S. Finney, P.J. Pospisil, M.L. Güler, T. Ishida, E.N. Jacobsen, J. Am. Chem. Soc., 1998, 120, 948-954
21. L. Deng, E.N. Jacobsen, J. Org. Chem., 1992, 57, 4320-4323
22. J.P. Simpson, (2014), Imperial Spectra DSpace, DOI:10042/149704 SS-epoxystilbene NMR Data
23. J.P. Simpson, (2014), Imperial Spectra DSpace, DOI:10042/149713 RR-epoxystilbene NMR Data
24. J.P. Simpson, (2014), Imperial Spectra DSpace, DOI:10042/149718 R-epoxystyrene NMR Data
25. J.P. Simpson, (2014), Imperial Spectra DSpace, DOI:10042/149723 S-epoxystryene NMR Data
26. J.P. Simpson, (2014), Imperial Spectra DSpace, DOI:10042/150162 RR-epoxystilbene Optical Rotation Data
27. J.P. Simpson, (2014), Imperial Spectra DSpace, DOI:10042/150155 SS-epoxystilbene Optical Rotation Data
28. J.P. Simpson, (2014), Imperial Spectra DSpace, DOI:10042/150083 R-epoxystyrene Optical Rotation Data
29. J.P. Simpson, (2014), Imperial Spectra DSpace, DOI:10042/150165 S-epoxystyrene Optical Rotation Data
30. D.E. White, E.N. Jacobsen, Tetrahedron: Asymmetry, 2003 , 14, 3633-3638
31. H. Toda, R. Imae, N. Itoh, Tetrahedron: Asymmetry, 2012 , 23, 1542-1549
32. H. Lin, J. Qiao, Y. Liu, Z-L Wu, J. Mol. Catal. B: Enzym., 2010 , 67, 236-241
33. H. Lin, Y. Liu, Z-L Wu, Tetrahedron: Asymmetry, 2011 , 22, 134-137
34. D.J. Fox, D.S.Pedersen, A.B.Petersen, S. Warren, Org. Biomol. Chem., 2006 , 4, 3117-3119
35. S.E. Denmark, H. Matsuhashi, J. Org. Chem., 2002 , 67, 3479-3486
36. Read, Campbell, Nature, 1930 , 125, 16
37. Read, Campbell, Nature, 1930 , 125, 16
38. H. Rzepa, (2013): Gaussian Job Archive for C20H26O7 DOI:10.6084/m9.figshare.822152 R-epoxystrene Transition State 1 (Shi epoxidation)
39. H. Rzepa, (2013): Gaussian Job Archive for C20H26O7 DOI:10.6084/m9.figshare.828520 R-epoxystrene Transition State 2 (Shi epoxidation)
40. H. Rzepa, (2013): Gaussian Job Archive for C20H26O7 DOI:10.6084/m9.figshare.822135 R-epoxystrene Transition State 3 (Shi epoxidation)
41. H. Rzepa, (2013): Gaussian Job Archive for C20H26O7 DOI:10.6084/m9.figshare.822137 R-epoxystrene Transition State 4 (Shi epoxidation)
42. H. Rzepa, (2013): Gaussian Job Archive for C20H26O7 DOI:10.6084/m9.figshare.823545 S-epoxystrene Transition State 1 (Shi epoxidation)
43. H. Rzepa, (2013): Gaussian Job Archive for C20H26O7 DOI:10.6084/m9.figshare.822136 S-epoxystrene Transition State 2 (Shi epoxidation)
44. H. Rzepa, (2013): Gaussian Job Archive for C20H26O7 DOI:10.6084/m9.figshare.828519 S-epoxystrene Transition State 3 (Shi epoxidation)
45. H. Rzepa, (2013): Gaussian Job Archive for C20H26O7 DOI:10.6084/m9.figshare.826003 S-epoxystrene Transition State 4 (Shi epoxidation)
46. Z-X Wang, Y. Tu, M. Frohn, J-R Zhang, Y. Shi, J. Am. Chem. Soc., 1997, 119, 11224-11235
47. H. Rzepa, (2013): Gaussian Job Archive for C36H44ClMnN2O3 DOI:10.6084/m9.figshare.860446 R-epoxystrene Transition State 1 (Jacobsen epoxidation)
48. H. Rzepa, (2013): Gaussian Job Archive for C36H44ClMnN2O3 DOI:10.6084/m9.figshare.860449 R-epoxystrene Transition State 2 (Jacobsen epoxidation)
49. H. Rzepa, (2013): Gaussian Job Archive for C36H44ClMnN2O3 DOI:10.6084/m9.figshare.860441 S-epoxystrene Transition State 1 (Jacobsen epoxidation)
50. H. Rzepa, (2013): Gaussian Job Archive for C36H44ClMnN2O3 DOI:10.6084/m9.figshare.860445 S-epoxystrene Transition State 2 (Jacobsen epoxidation)
51. W. Zhang, J.L. Loebach, S.R. Wilson, E.N. Jacobsen, J. Am. Chem. Soc., 1990, 112, 2801-2803
52. H. Rzepa, (2013): Gaussian Job Archive for C26H30O7 DOI:10.6084/m9.figshare.828552 RR-epoxystilbene Transition State 1 (Shi epoxidation)
53. H. Rzepa, (2013): Gaussian Job Archive for C26H30O7 DOI:10.6084/m9.figshare.830388 RR-epoxystilbene Transition State 2 (Shi epoxidation)
54. H. Rzepa, (2013): Gaussian Job Archive for C26H30O7 DOI:10.6084/m9.figshare.829522 RR-epoxystilbene Transition State 3 (Shi epoxidation)
55. H. Rzepa, (2013): Gaussian Job Archive for C26H30O7 DOI:10.6084/m9.figshare.829523 RR-epoxystilbene Transition State 4 (Shi epoxidation)
56. H. Rzepa, (2013): Gaussian Job Archive for C26H30O7 DOI:10.6084/m9.figshare.829524 SS-epoxystilbene Transition State 1 (Shi epoxidation)
57. H. Rzepa, (2013): Gaussian Job Archive for C26H30O7 DOI:10.6084/m9.figshare.829525 SS-epoxystilbene Transition State 2 (Shi epoxidation)
58. H. Rzepa, (2013): Gaussian Job Archive for C26H30O7 DOI:10.6084/m9.figshare.830389 SS-epoxystilbene Transition State 3 (Shi epoxidation)
59. H. Rzepa, (2013): Gaussian Job Archive for C26H30O7 DOI:10.6084/m9.figshare.830390 SS-epoxystilbene Transition State 4 (Shi epoxidation)
60. H. Rzepa, (2014): Gaussian Job Archive for C42H48ClMnN2O3 DOI:10.6084/m9.figshare.899176 RR-epoxystilbene Transition State (Jacobsen epoxidation)
61. H. Rzepa, (2014): Gaussian Job Archive for C42H48ClMnN2O3 DOI:10.6084/m9.figshare.903625 SS-epoxystilbene Transition State (Jacobsen epoxidation)
62. D. Wirth, W. Boland, D.G. Mueller, Helv. Chim. Acta., 1992 , 75, 751-758








