Rep:Mod:JPS1122

Module 3 - Transition Structures of Cope Rearrangements and Diels-Alder Reactions (James Simpson CID:00733493)

During the course of these computational exercises the transition structures of both the Cope rearrangement and Diels Alder cycloaddition reactions will be characterized. The transitions states for the Cope rearrangent will be found using different 1,5-hexadiene conformers. The same will be done with Diels-Alder reactions, firstly with the prototype reaction and secondly with the addition of 1,3-cyclohexadiene and maleic anhydride. For this more complex example the differences in the two products will be identified and explained. The HOMO and LUMO of the reactants and the transition state will be used to aid this.

Introduction

Chemistry

Cope Rearrangement

The Cope rearrangement was discovered by Arthur Cope¹ and is a [3,3]-sigmatropic shift of a 1,5-diene²: this means that there is an allyl migration occurring. It is a concerted pericyclic reaction² and heat is required for the reaction to occur; as the number of electrons involved in the reaction is 6 it proceeds, with suprafacial components^3,4, via a Hückel topology. It is also possible for the transition state, which exists as a chair-like structure, to be stabilized due to its aromatic nature. The reaction is very similar to the Clasian rearrangement which involves an oxygen heteroatom in the [3,3]-sigmatropic shift instead of purely carbon atoms.

Diels-Alder Reaction

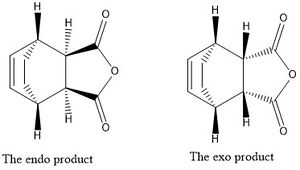
The Diels-Alder reaction, discovered by Otto Diels and Kurt Alder⁵ is a cyclo-addition of a conjugated diene and an alkene: indeed it is the simplest cyclo-addition. The electron count is 6; 4 π electrons come from the conjugated diene and 2 π electrons from the alkene². Heat is needed for the reaction to occur and so the reaction has suprafacial components via a Hückel topology. When the conjugated diene and alkene are substituted the reaction can have two products; the exo and endo products. These two products come about from different transition statesstructures: the endo product transition state has the diene's substituents facing towards the π system of the diene but in the case of the exo product the opposite is true. The reaction occurs through a cyclic aromatic-like transition state although a diradical intermediate has also been proposed⁶.

The stereochemistry of the two different products, the endo and exo, can be compared in the diagram below.

Computation

Gaussian

Gaussian is a program used for computational and quantum chemistry originally created in 1970; the latest version is G09⁷. Gaussian orbitals are used instead of Slater-type orbitals in order to speed up computational time when using Hartree Fock calculations. The program can be used for many different calculations, including Hartee Fock method and density functional theory; both of these are used during the course of this experiment. Synchronous Transit-Guided Quasi-Newton calculations are also done in this experiment in order to optimize the potential boat conformer of the Cope arrangement of 1,5-hexadiene. The intrinsic reaction coordinate will be used also, in order to find the conformer that the optimized chair and boat conformers will lead to.

Hartree Fock Method

The Hartree-Fock method is a method that is commonly used in molecular orbital interactions^8,9 and can be used in order to approximate the wave function and the energy of a many-body system in a stationary state. It works by assuming that the wave function can be approximated with a single Slater determinant if the particles involved are fermions or with a single permanent, which is a function similar to the determinant of a square matrix, if the particles involved are bosons. In this experiment nuclei and electrons are used and so the approximation will be made using a Slater determinant. The method therefore is an approximation of the Schrödinger equation and calculations made using the method are usually solved iteratively.

Density Functional Theory

One of the methods used in this experiment is density functional theory: this is a computational method which calculates the properties of a molecule using the electronic structure of that system - usually the ground state is used. In this method the properties are found by functions of other functions, in this case the spatially dependent electron density.

Synchronous Transit-Guided Quasi-Newton Method

The synchronous transit-guided quasi-Newton method is a method which combines both the synchronous transit and the quasi-Newton method¹⁰ in order to optimize a transition state. The synchronous transit method finds an approximate transition state and then the quasi-Newton method finishes the optimization. For this approach a guess of the transition structure is not required as only the reactant and the product are needed. As two molecules will be used to do this, the reactant and product, then the exact method is called QST2.

Intrinsic Reaction Coordinate Method

The intrinsic reaction coordinate method allows for the process of a reaction to be followed computationally. This is done by following a minimum energy path from the reaction to the transition state then following the path further to the product. The minimum energy is self explanatory and can easily be seen as the low energy valley of a potential surface. However for these types of calculations to be carried out the transition state's structure must already be known.

Austin Model 1

The Austin Model 1 or AM1 is a semi-empirical computational method used in Gaussian in order to solve electronic structure calculations. It works using a modified version of the differential diatomic overlap approximation. This is called the neglect of differential diatomic overlap-integral approximation.

(This computational introduction is roughly ok. It should only be clear that Hartree-Fock, DFT and AM1 are different methods and approximations to calculate quantum mechanical energy of the electrons for a given nuclear configuration. The electronic energy as a function of the nuclear coordinates is the PES, and QST2, IRC, etc. use first and eventually second derivative of this energy to obtain nuclear configurations/molecular geometries that correspond to interesting features of the PES and consequently of the chemical reaction João (talk) 19:11, 23 December 2014 (UTC))

The Cope Rearrangement

Optimizing the Reactants and Products

The Cope rearrangement is a reaction that in the past has been extensively studied. In order for this to be done computationally the structure of a 1,5-hexadiene must be optimized; in this case the simplest molecule that could undergo a Cope rearrangement was 1,5-hexadiene itself. This was done in order to find the point group and the energy of a particular conformer of 1,5-hexadiene. The optimized structure of an antiperiplanar arrangement of 1,5-hexadiene and a gauche arrangement of 1,5-hexadiene can be found below using the Hartree Fock method and the 3-21G basis set. The energies and point group of these conformers can be seen in the table below. It was expected that an antiperiplanar conformer would have a lower energy than any gauche conformer, due to there being σσ^* interactions between the C-H and C-C on the saturated carbons. It was also possible that there would be some favourable interactions between the σ and π bonds on the terminal C-C bonds. However it can be seen from the table below and from the lab script¹¹ that the lowest energy conformer was the gauche 3 conformer. This was not what was expected, meaning that there were favourable interactions, possibly between the C-H σ bond and the C-C π bond, that occurred in this gauche conformer because there was a periplanar arrangement at the termini of the molecule. This interaction does not occur in any other conformer, although it is also possible that the gauche 3 conformer is not in fact the lowest energy conformer and that it is only found to be the lowest energy conformer because of the computational method used.

Energies and Point Groups of Conformations of 1,5-Hexadiene Conformers

Antiperiplanar(1) Conformer

Gauche(4) Conformer

Lowest Energy Conformer (Gauche 3)

Antiperiplanar(2) Conformer

Model

Energy (Hartree)

-231.69260236

-231.69153027

-231.69266119

Point Group

C2

C1

Ci

In the lab script for this experiment the energy and point groups of the lowest 10 energy conformers are shown. From this information it can be clearly seen that the antiperiplanar conformer found was the anti1 conformer and the gauche conformer found was the gauche4 conformer. The anti2 conformation of 1,5-hexadiene was also found and is shown in the table above: it has the point group Ci and its energy was also calculated. After the molecule was optimized it was re-optimized using a different basis set, the B3LYP/6-31G* set, which was done using density functional theory instead of using the Hartree Fock method. This gave a different energy from that calculated previously, -234.61171063 compared to -231.69266119, because of the differences between the computational methods as they take account of different things. (Such as? Which do you expect to be more accurate? João (talk) 19:11, 23 December 2014 (UTC)) (How do the two optimized geometries compare to each other? João (talk) 19:11, 23 December 2014 (UTC))

Thermochemistry Infomation of the 1,5-Hexadiene Molecule
	At 298.15K	At 0.01K
Sum of Electronic and Zero-point Energies	-234.469219	-234.469219
Sum of Electronic and Thermal Energies	-234.461869	-234.469219
Sum of Electronic and Thermal Enthalpies	-234.460925	-234.469219
Sum of Electronic and Thermal Free Energies	-234.500809	-234.469219

Note that all the energies stated are in Hartrees. After the Anti2 conformer was optimized the vibrations of the molecule were computed again using density functional theory. This was done successfully as there were no imaginary frequencies found (What is the significance of this fact? João (talk) 19:11, 23 December 2014 (UTC)). The simulation was done at 298.15K and from this several pieces of information relating to the thermochemistry of the system could be found. These are shown opposite at both 298.15K and at 0.01K. The sum of the electronic and zero-point energies is simply the potential energy of the system at 0K: there will be a zero-point vibrational energy at absolute zero which is included in this energy. It should be noted that the sum did not change when the calculation was done with different temperatures. This was as expected as the sum of the electronic and zero-point energy is the minimum energy of the system and so, as the molecules were the same (Would it be different for a different conformer? Is it a different molecule? João (talk) 19:11, 23 December 2014 (UTC)), the energies should be the same. The second energy is the sum of the electronic and thermal energies, which is the sum of the rotational, translational and vibrational energies at that temperature and at 1atm. The sum of the electronic and thermal enthalpies shows the same as the sum of electronic and thermal energies but with a correction for the enthalpy of the system, not just the energy. The difference of the energy of the system and the enthalpy is proportional to the temperature of the system. The final energy calculated, which was the sum of electronic and thermal free energies, included the entropy of the system; this difference between the Gibbs free energy and the enthalpy of the system is simply the entropy of the system multiplied by the temperature.

At 0.01K the system is almost at absolute zero and this means that the difference between the energy of the vibrational, rotational and translational modes and the enthalpic correction, and between the thermal enthalpy and the thermal free energy, is also zero. All of these values for the molecule, which has C_2v symmetry, are also exactly equal to the sum of the electronic and zero-point energy. This is because at 0.01K there was no vibrational nor rotational nor translational energies occuring in the system.

Optimizing the "Chair" and "Boat" Transition Structures

Cope Chair Transition State

The reaction can proceed with two different transition state geometries, either with a chair conformer or a boat conformer. Firstly an allyl fragment, C₃H₅ was made and then optimized, using the Hartree Fock method and a 3-21G basis set. Two of these fragments were then arranged in a chair conformer, so that the distance between the carbons that form and/or break a bond was 2.2Å. This chair structure was then optimized using two different methods, in order to see whether or not the output, the optimized geometry, was affected. The two methods used were the frozen coordinate method and the other was done by using the Hartree Fock method to optimize the transition state (This is incorrect: Hartree-Fock is a method to calculate the electronic energy, not to find a transition state João (talk) 19:11, 23 December 2014 (UTC)). The Hartree Fock method has already been discussed and so will not be discussed again but the frozen coordinate method has not been. In this method the carbon atoms at the termini of each fragment are frozen in the correct position for bond formation, 2.2Å (Why is this the "correct" position? Was this the value you obtained with the Berny algorithm? João (talk) 19:11, 23 December 2014 (UTC)), and then the system was optimized as normal. (This is actually a two step procedure. If you obtained the same structure as you suggest bellow, then you are missing the description of one of the steps João (talk) 19:11, 23 December 2014 (UTC))



Vibration Corresponding to Cope Rearrangement

It was found that both approaches gave the same structure, which can be seen above and on the right. The vibration that corresponds to the Cope rearrangement was then found (How did such vibration make it self found? João (talk) 19:11, 23 December 2014 (UTC)). The video of this vibration is found to the left. As can be seen from the gif the vibration clearly corresponds to bond formation/breaking. Next it was necessary to optimize the transition structure of the boat conformer. The first method used to do this was the QST2 method. This was done by drawing the structure of the product and reactant molecules, making sure the atoms in the system were all tagged, this made it clear which bond was broken and which was made. Doing this gave a strange result, which can be seen below and to the right. It is clear the structure was incorrect and that it looks very like the chair transition state. The calculation was done by interpolating between the reactant and product molecules and so one of the allyl fragments was just translated. This means that the method does not consider that the central bonds can rotate and so a different method is, therefore, required. From the file that was used to set up the failed QST2 calculation it was possible, using a different approach, to find the boat transition structure. This was done by making sure that of the structure of the product and reactant was closer to the expected transition structure. The dihedral angle between the four central carbons was set to be 0^o. The inside angles were then set to be 100^o. The QST2 calculations were then run again. The results of this are shown below.

Boat Conformer

Failed Cope Boat Transitions State

Cope Boat Transitions State

Cope Rearrangement Vibration

Now that the transition states have been found it can be considered which conformer they connect to. However within gaussian it is possible to follow the minimum energy path of the reaction. This is called the intrinsic reaction coordinate. The method was run in only one direction as the reverse reaction, in this case, is the same as the forward reaction and the force constant of the reaction was calculated at each step in the reaction. The number of points that the reaction was run for was set to 50. After this was done, as the minimum energy of the conformer was not reached, three things could be done in order to optimize the conformer. The first of these methods was to simply run an optimization to a minimum potential of the last point of the IRC. This will only work if the final point on the IRC is quite close to the energy of the product. The second of these methods was to restart the IRC and to run it for longer, i.e. for a larger number of points. This can be useful, but the reaction can go a direction different to the one wanted. The third thing that could have been done is to rerun the IRC but calculate the force constants at every point. The major problem with this is that it can be expensive if the system is larger. It should be noted that a combination of all three of these methods could also be employed. (Which one did you choose to do? João (talk) 19:11, 23 December 2014 (UTC))

The Product Conformer from the Optimized Chair Transistion Structure using IRC

The Product Conformer from the Optimized Boat Transistion Structure using IRC

It is clear from the diagram on the left that the product of the reaction when the transition state is in a chair conformer corresponds to the gauche 2 conformer. However when the transition state is in a boat conformer the product of the reaction, as calculated using IRC does not correspond to any of the conformers given in the lab script. This suggests that a potential minimum has not been found. The reasons for this are not clear as all three methods previously mentioned, in the lab script, were used in order to find the conformer of the product. It is possible, therefore, that the transition state found for the boat transition state was not exactly correct. The final thing to be mentioned about the boat conformer product is that the ends of the molecule look a bit like the gauche 3 conformer, except that there is an antiperiplanar arrangement instead of a gauche arrangement (It looks like an eclipsed conformation to me João (talk) 19:11, 23 December 2014 (UTC)). However more calculations must be run in order to investigate this further.

The final thing that can be done with the Cope rearrangement is to work out the activation energy of the reaction. This is done by reoptimizing the transition structure using Hartree Fock and then carrying out frequency calculations (If you are re-optimizing at the Hartree-Fock level, at what level was the first optimization made? João (talk) 19:11, 23 December 2014 (UTC)). The aza-Cope rearrangement, which is similar to the Cope rearrangement but with one carbon atom replaced with a heteroatom, specifically a nitrogen atom, is known to happen under kinetic control of the transition state¹²: therefore it is likely that the case is the same in the Cope rearrangement. This means that the activation energy would be expected to be lower for the chair transition state than for the boat transition state. The results of these calculations are simply the differences in energy between the anti 2 conformer and the corresponding transition state. Indeed it is seen that the reaction via a chair transition state requires less energy and so is the pathway that the reaction will follow. The values of these energies are higher than those found in literature for the chair conformer, 35.5kcalmol^{-1 11,13} and the reason for this is that Hartree Fock was used for the reoptimizations. It is a less accurate computational method and so the energies calculated will be less accurate than other possible methods. However the values agree with those found computationally using the Hartree Fock method¹¹.


	Chair Transition State	Boat Transition State
Energy of Transition State (Hartree)	-231.61932244	-231.60280249
Activation Energy (Hartree)	0.07333875	0.0898587
Energy of Transition State (kcalmol^-1)	46.020770266	56.38719762

The Diels-Alder Cycloaddition

The second part of this exercise involves a Diels-Alder reaction, which is a pericyclic addition. The transition structure of the prototype reaction, 1,3-cisbutadiene and ethene will be found and for a more complicated Diels-Alder reaction the transition state for both the endo and exo products will be found. In addition the HOMO and LUMOs of the molecules will also be calculated and discussed. In this class of reactions if the HOMO of one molecule can react with the LUMO of another molecule then the reaction can occur in one concerted step. For there to be an interaction then the energies of these orbitals must be close in energy, have overlap density and the same symmetry properties. For reactants that have groups other than hydrogen, all Diels-Alder reactions apart from the prototype have secondary orbital overlap effects and these interactions influence the regiochemistry of the reaction. All the interactions and effects that govern the reaction are of course quantum mechanical in nature and so the computations that calculate the required infomation in this task must be based on quantum chemistry.

The Prototype Diels-Alder Reaction

The HOMO and LUMO of 1,3-Cisbutadiene
HOMO	LUMO
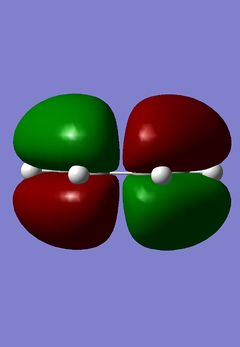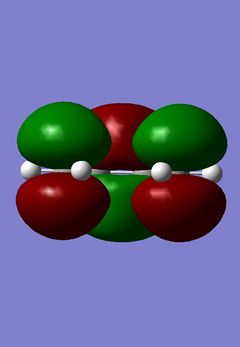The HOMO of Cis-butadiene	The LUMO of Cis-butadiene

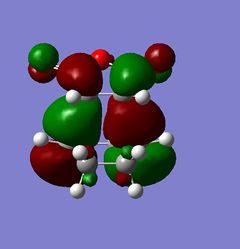
The simplest Diels-Alder reaction is that of 1,3-cisbutadiene and ethene, this is known as the prototype reaction. In the reaction the HOMO of the 1,3-cisbutadiene molecule interacts with the LUMO of the ethene molecule. The symmetry of both orbitals in this case are a, meaning they are anti-symmetric with respect to the reflection plane going through the centre of the molecule. The LUMO of 1,3-cisbutadiene molecule also interacts with the HOMO of the ethane molecule. The symmetry of these orbitals is s, meaning they are symmetric with respect to the reflection plane going through the centre of the molecule. There are two HOMO LUMO interactions and two new σ bonds are formed. The first thing done was to build the 1,3-cisbutadiene molecule using Gaussian and then to optimize it using the Austin Method 1, AM1. The HOMO and LUMO of the molecule were then found. There two ways to do this, the first was to edit the MOs in the Gaussian menu and then to visualize them. The second, if having previously calculated the orbitals, was to display them on the main Gaussian window using the surfaces option in the results menu. The orbitals were then calculated and then obtained; the results of this are shown above and on the left:

The models show exactly what was predicted. Then, using the plane of symmetry that goes through the molecule, it is clear that the HOMO of 1,3-cisbutadiene is antisymmetric and the LUMO of the same molecule using the same plane is symmetric. The next step was to find the structure of the transition state of the prototype Diels-Alder reaction. This was done by building a bicyclo system, the result of two Diels-Alder reactions, and optimizing the structure using AM1. This structure then had one -CH₂-CH₂- fragment removed and the distance between the carbons in the remaining cycle, the product of one reaction, increased to 2.2Å. The bond angles were changed in order to make them closer to the product, this was done by increasing the sp² character of the terminal C-C bonds. A Berny transition state was then calculated using AM1. This transition structure can be seen below: (How are you sure you obtained a transition state? João (talk) 20:15, 23 December 2014 (UTC))

The Transition State for the Prototype Diels-Alder Reaction

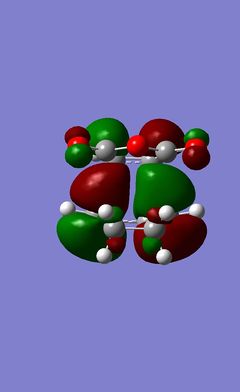
Transition State

HOMO

LUMO

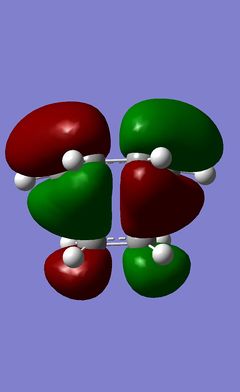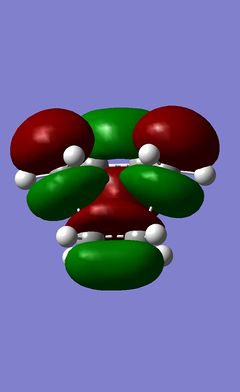From the geometry of the transition state the reaction path can be examined (What can you say about the reaction path? João (talk) 20:15, 23 December 2014 (UTC)). The structure maximizes the overlap between the π systems of the ethene molecule and the system found in the 1,3-cisbutadiene. Using either of the methods described earlier it was again possible to visulize the HOMO and LUMO orbitals of the transition state and from this the symmetry of the orbitals for the plane of symmetry through the molecule can be determined. These are shown below. The HOMO and LUMO should, of course, be similar to this prototype reaction for more complicated Diels-Alders but without the secondary orbital interactions that can occur in these more complicated systems. However the symmetry of both the HOMO and the LUMO must be determined. It is clear from the table, however, that the symmetry, when using the molecule's plane of symmetry, is antisymmetric, with respect to the plane of symmetry for the HOMO and that the LUMO's symmetry is symmetric with respect to the plane of symmetry that goes throught the centre of the molecule.

Maleic Anhydride and 1,3-cyclohexadiene

This is the more complicated example that will be studied. This is done in order to compare the two different products of the reaction that can be formed, the exo product and the endo product. The differences in the structure of these products is shown in the introduction of this wiki page. The reaction is controlled kinetically¹⁴ and the endo product is the major product of this reaction. This suggests that the exo transition state is higher in energy that the endo transition state and so requires a larger activation energy. In order to do this, in much the same way as for the previous example, the structure of the products was drawn out and then changed to be in an inbetween stage of the reactants and the product. The Berny transition states were then compared, and the results of this can be seen below:

Structure and Energies of the Endo and Exo transitions states

Endo

Exo

Transition State Structure

HOMO Structure

Energy of Transition State

-0.05150480

-0.05041979

Energy of Product

-605.72132045

-605.71873543

It has already been stated that the reaction is kinetically controlled. The results obtained in the table agree with this. This is because the energy of the endo transition state is lower than the energy of the exo transition state and so if the reaction takes place from the same starting molecules, more energy will be required to reach the transition state that will give the exo products. This is why the endo product for this reaction is favoured. Much can be gained from looking at the structure of the transition state of both products and it is clear that the structure is a compromise between the steric repulsions of the groups added between this reaction and the prototype. The other factor is the secondary orbital overlap that may present in both cases, but which must make the endo transition state more favoured. It is noticable that the symmetry of both HOMOs is antisymmetric with respect to the plane of symmetry that runs through the product molecules. This is as was expected as the HOMOs should be fairly similar to the HOMO of the prototype reaction between ethene and 1,3-cisbutadiene. However from inspection of the HOMOs of both transition structures there are no obvious secondary orbital interactions, but from inspection of the HOMO -1 orbital, it is clear that there is a secondary orbital interaction between the p like orbital on the carbonyl oxygen and the partly formed π system of the ring that is being formed. This interaction does not occur in the exo transition state due to the orientation of the atoms.

The HOMO -1 of the Endo Transition State
The HOMO -1 of the Endo Transition State

Finally the steric interactions can be considered to determine if that has any meaningful effect on whether or not the endo product is favoured over the exo or if it is simply due to secondary orbital interactions. The bond lengths of all the C-C bonds were measured in order to determine sp³ versus sp² character of the system (this will be discussed later) as was the distance between the carboxyl carbons and the nearest carbons, the -CH₂CH₂- group for the exo transition state and the -CHCH- group for the endo product. It is expected that the transition structure of the exo product will have some steric repulsion. The results of this are shown in the following table below:

The C-C Bond Distances in the Exo and Endo Transition Structures
	Endo	Exo
Partly Formed C-C Bond Distance	2.17034	2.16239
Distance Between Carboxyl Carbon and the Nearest Relevant Carbon	2.94494	2.89222
Distance Between Carboxyl Carbon and Hydorgen Bonded to Nearest Relevant Carbon	2.41624	3.08311

The partly formed C-C bond distances for both structures are similar, which is as expected. However it can be seen that the relevant carbon distances are closer together for the endo transition structure that for the exo transition. This is clearly not the only interaction as it would suggest that the exo product is sterically less strained than the endo. However if the hydrogens on the double bond-forming carbon are also considered it can be seen, due to the hydrogens on the bond forming carbon being sp² like and on the -CH₂CH₂- bridge being complety sp³ hybridized, that the hydrogens will stick out towards the maleic anhydride in the exo transition state. The Van der Waals radius of carbon is 1.7Å and 1.2Å for hydrogen¹⁵. This C H unfavourable interaction is much stronger in the exo transition state, due to the shorter distance. So it is the lowering of the energy of the molecular orbitals for the endo transition as well as the steric clash arising in the exo transition state that makes the endo product more favourable.

Discussion

It is of course true that the transition state for all reactions is inbetween the reactants and products. However it is not immediately known whether the bonds are closer to the reactants or the products: this can be done by looking at the C-C bond distances in the forming ring. The σ bond formed will, of course, be closer together. The results of these bond distances can be summerized in the table below, along with the the vibration that corresponds to the reaction. It should be noted the bond order written is the bond order of the reatcants:

Bond Distances of Diels-Alder Reactions
	Prototype	Exo	Endo
Reaction Vibration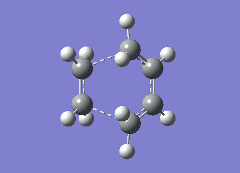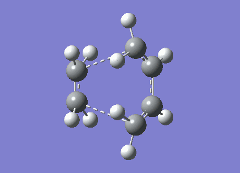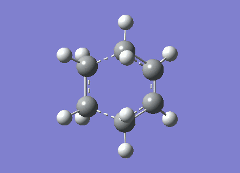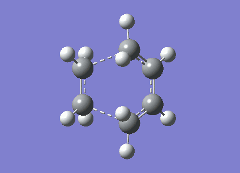
Double Bond (1,3-Cyclohexadiene/1,3-Cyclohexadiene Derivative)	1.48331	1.39436	1.39305
Single Bond (1,3-Cyclohexadiene/1,3-Cyclohexadiene Derivative)	1.41399	1.39680	1.39724
Double Bond (Ethene/Ethene Derivative)	1.54000	1.41000	1.40849

From the table it is clear that the bond lengths are shorter for the non prototype reactions. For reference the average C-C bond length is 1.52-1.58Å¹³, however for a C-C single bond inbetween two double bonds, the average bond length is 1.40-1.46Å¹³. This is because the bond is inbetween two sp² hybridized carbons. The average C=C bond length is 1.29-1.34Å¹³. From this it is clear that for all three reactions the transition state is closer to the products than to the reactants in structure. However for the more complicated Diels-Alders reactions this transition state is, relative to the prototype reaction, closer to the reactants. The last piece of infomation in the table is the vibration that corresponds to the reaction. It is seen that for all the cases the σ bonds formed are formed at the same time, as is expected.

For the Diels-Alder reaction of 1,3-hexadiene with maleic anhydride it has been shown that there are two products and the energies of these products were found to be -605.72132045 Hartrees for the endo product and -605.71873543 Hartrees for the exo product. This is odd as the endo form is in fact less stable than the exo product but as the reaction is kinetically controlled (The fact the raction is kinetically controlled is related to the energy of the products or of the transition state? João (talk) 20:15, 23 December 2014 (UTC)), and due to secondary orbital overlap, the endo product is the major product. There is a structural difference between the two products of the reaction between 1,3-cyclohexadiene and maleic anhydride. As can be seen in the introduction of this lab script the endo product forms with the 'bridge' over the formed Diels-Alder ring and with the maleic anydride ring pointing in opposite direction, one up and one down. The exo product gives the opposite of this with both the secondary ring and the 'bridge' on the same face of the molecule. The secondary orbital effect in this reaction must, of course, be quite large in order to sufficiently lower the energy of the endo transition state so that the reaction proceeds down that path over the competing exo path. Throughout this experiment certain effects have been neglected, the most important of these are solvent effects which will, of course, effect the reactivity of the system, due to interactions of the reactant molecules with the solvent. The second of the effects that has been ignored is the effect of more molecules of the reactants. In the computations there have only ever been enough molecules present to make one molecule of product: however if the reactants can react with themselves more readily than they react with the other reactant then the reaction might not occur. It is known that 1,3-cyclohexadiene can self dimerize¹⁶, both thermally in the gas phase¹⁴ and reductively in ammonia¹⁷. Indeed 1,3-butadiene, which reacts in the prototype, will dimerize with itself and can, under certain conditions, polymerize.

Conclusion

During the course of these computational exercises the transition structures of both the Cope rearrangement and Diels Alder cycloaddition reactions were characterized using quantum mechanics. The energies of different 1,5-hexadiene were found in order to determine the reaction mechanism of the Cope rearrangement. These conformers were also identified and the lowest energy conformer determined. Once this was done the transition structure for each of the possible transition states for the Cope rearrangement was determined and the activation energy of both the reaction pathways were determined. The value for the chair conformer was then compared to literature and the reason for the difference was then discussed. In addition the conformer that each transition state corresponded to if the minimum energy path is followed was determined.

In the second part of the experiment, the Diels-Alder reaction was investigated. The HOMO and LUMO of one of the reactants in the prototype reaction, 1,3-cisbutadiene, was found and it was determined what the symmetry of each the molecular orbitals was and which molecular orbital of the other reactant, ethene, the HOMO and LUMO of 1,3-cisbutadiene will react to. After this was done the transition state of the prototype reaction was optimized and the HOMO of this transition state found and its symmetry determined. More complex Diels-Alder reactions were also investigated, specifically 1,3-cyclohexadiene and maleic anhydride. The two different transition structures for the endo and exo products were looked into in order to explain why the reaction, under kinetic control, forms the endo product. This was found to be due to secondary orbital overlap in the endo transition structure and steric clash in the exo transition state.

In addition the geometry of the transition structure was found: this was done by measuring the bond distances in the Diels-Alder ring, including the partly formed bonds. It was also determined that the transition states for the Diels-Alder were closer in energy to the products than the reactants and the vibrations that correspond to the reaction path found. It was found that the bond formation was synchronous. The relative endo and exo transition structures' energies were found showing that indeed the reaction occur with kinetic control. Finally the effects that were neglected in these calculations were considered.

References

1. A. C. Cope; et al.; J. Am. Chem. Soc. 1940, 62, 441

2. H. Rzepa's Teaching e-materials, http://www.ch.ic.ac.uk/rzepa/, (accessed 24 Nov-5 Dec)

3. R.B. Woodward, R. Hoffmann, J. Am. Chem. Soc., 1965, 87, 2511

4. R. Hoffman, K. Fukui, J. Am. Chem. Soc., 1967, 87, 395

5. O.P.H. Diels, K. Alder, Liebigs Ann., 1928, 460, 98-122

6. M.J.Dewar, S. Olivella, J.J. Stewart, J. Am. Chem. Soc., 1986, 108, 19

7. Gaussian 09 Revision D.01 Release Notes (published 4 June 2013)

8. F.P. Boer, M.D. Newton, W.N. Lipscomb, Proc. Natl. Acad. Sci. U.S.A., 1964, 52, 890-893

9. F.P. Boer, M.D. Newton, W.N. Lipscomb, Proc. Natl. Acad. Sci. U.S.A., 1965, 53, 1089-1091

10. C. Peng, H.B. Schlegel, Isr. J. Chem., 1993, 33, 449-454

11. Imperial College Chemistry Wiki, https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3, (accessed 24 Nov-5 Dec)

12. M. Lukowski, K. Jacobs, P. Hsueh, H.A. Lindsay, M.C. Milletti, Tetrahedron, 2009, 65, 10311-10316

13. R. Hoffman, W.D. Stohrer, J. Am. Chem. Soc., 1971, 93, 6941-6948

14. G. Just, U. Linder, W. Pritzkow, M. Rollig, J. Prakt. Chem., 1975, 317, 979-989

15. G. Gafner, C.M. Lee, F.H Herbstei, Acta. Crystall. A-Crys., 1972, 28, 422

16. R.T. Sanderson, Science., 1952, 116, 41-42

15. G.R. Demare, G. Huybrech, M. Toth, P. Goldfing, J. Chem. Soc. Faraday Trans., 1971, 67, 1397

16. D.Y. Myers, R.R. Grabbe, P.D. Gardner, Tetrahedron Lett., 1973, 7, 533-536

17. Y. Li, K.N. Houk, J. Am. Chem. Soc., 1993, 115, 7478-7485