Rep:Mod:JPS

Physical Computational Lab: Module 3

This series of sections details the procedures taken to calculate reaction transition states and potential energy surfaces of various organic molecules.

Cope Rearrangement Tutorial

This section details the computational procedures taken to investigate the conformations of 1,5-hexadiene, and the transition states involved in the Cope Rearrangement. The structure of this molecule theoretically permits 27 conformations which, due to symmetry restrictions, reduce to an overall 10 energetically distinct forms.^[1]The rotation about the single bonds permits the two different transition states discussed in this section, giving differing activation energies of the rearrangement, along with different transition state energies.

Optimizing the Reactants and Products

The aim of the first part of this investigation was to study a [3,3]-sigmatropic rearrangement through locating the transition structures and low energy minima of the potential energy surface, and by determining the reaction mechanism.
To begin, a molecule of 1,5-hexadiene was drawn in GaussView, with an approximate anti-periplanar (app) relationship between the central two carbon atoms. The structure was then optimised to the HF/3-21G level and then symmetrized - the search criteria had to be relaxed to loose - in order to find the point group.

The dihedral angle of this conformation was then adjusted to form a gauche conformation and the same calculations carried out. The quantities obtained from these calculations are summarised below:

Arrangement	Energy(au)	Energy(kcal/mol)	Point Group
Antiperiplanar	-231.688	-145386.45	C₂
Gauche	-231.689	-145387.07	C_2h

Due to steric hinderance, it was predicted that the gauche formation would be higher in energy than the antiperiplanar however, as has been previously reported^[2], the difference in energy between the gauche and antiperiplanar conformations is very small. This implies that in both arrangements, the energies of the stabilising σ-interactions between σ_C-C-σ*_C-H, in the gauche conformation, and σ_C-C-σ*_C-C in app are very similar.
The anti2 structure was then drawn and optimised in the same way as before, and was found to have C_i point group. It was then optimised further using B3LYP/6-31G*, which lowered the energy by approximately 3au (1900kcal/mol) and changed the dihedral angle of H-C-C-H from 5.23° to 3.87°. This therefore brought the structure closer to the theoretical angle of 0°.
In order to calculate if this state is a minimum, the vibrational frequencies were calculated. This was done by running a B3LYP/6-31G* calculation, but changing the optimize field to frequency. This allowed an IR spectrum to be generated (42 modes) and the individual vibrations of the molecule to be viewed. The computationally generated spectrum can be seen here. No imaginary (negative) frequencies were found. The thermochemical data from this calculation was then retrieved, giving the values listed in the table below:

Energy Calculation	Meaning	Value(au)	Value(kcal/mol)
Sum of electronic and zero-point Energies	E = E_elec + ZPE	-234.469203	-147131.67767
Sum of electronic and thermal Energies	E = E + E_vib + E_rot + E_trans	-234.461858	-147127.068612
Sum of electronic and thermal Enthalpies	H = E + RT	-234.460914	-147126.47624
Sum of electronic and thermal free Energies	G = H - TS	-234.500774	-147151.48878

The first of these values represents the potential energy of the molecule at 0K including the zero point vibrational energy. The second is the energy at 298K and 1atm, including contributions from the translational, rotational, and vibrational energy modes. The third term includes a correction for RT, and the fourth includes the entropic contribution to the free energy.

Optimizing the Chair and Boat Transition Structures

This section involves investigating the chair and boat transition states of the Cope rearrangement in order to calculate their relative energies and the activation energy of the reaction.

Chair Transition State

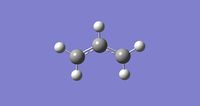
Firstly, an allyl fragment was drawn and optimised using the HF/3-21G level to produce the structure shown on the right hand side. This optimised C₃H₅ fragment was then arranged with another identical fragment, with the distance of the terminal ends of the allyl fragments approximately 2.20Å apart.
A transition state optimisation was then run using HF/3-21G. The force constants were set to be calculated once, and the additional keyword Opt=NoEigen was used to prevent the calculation from stopping if an imaginary frequency was detected. This calculation gave a vibrational excitation at -817.94nm, corresponding to the motion with which covalent bonds would form between the two ends of the allyl fragment. This structure was then optimised by freezing the coordinates of the atoms at the ends of the allyl groups. This gave an optimised structure, but with the distances at either end of the chains fixed to 2.20Å. The checkpoint file from this calculation was then used in a similar manner, but in this case, the aim was to optimise the distances between the two C₃H₅ fragments. Following optimisation, the distance between the ends of the allyl fragments was found to be 2.02Å, a picture of which can be seen on the left hand side. This value of 2.02Å is almost identical to the originally optimised structure from the beginning of this section.

Boat Transition State

The previously optimised C_i point group anti 2 structure was used, and separate products and reactants windows were created for 2 of these optimised molecules. These were numbered as shown to ensure the subsequent calculation proceeded as required.

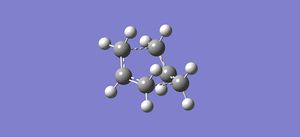
A QST2 Opt+Freqcalculation was then performed on these two molecules, producing the shown transition state. This calculation failed as it did not take into account rotation and simply translated the top allyl fragment, producing something which closely resembles a chair structure. A second calculation therefore had to be run, but with the dihedral and bond angles changed. The C₂-C₃-C₄-C₅ dihedral angle in the reactant molecule was changed to 0°, and the C₂-C₃-C₄ and C₃-C₄-C₅ angles changed to 100°. The same was done for the corresponding carbons in the product molecule. The same calculation as before was then run, giving the expected transition state, as shown.

Interpretation of Generated Transition States

Intrinsic Reaction Coordinate

It is difficult to determine from the transition structures of the two states, which conformer of 1,5-hexadiene will be formed by that reaction. However, by looking at the transition state for the boat structure, it could be argued that this would form the gauche 1 structure. Nevertheless it is much harder to simply visualise the structure that would form from the chair transition state. These are merely speculations and therefore more rigorous calculations must be performed.
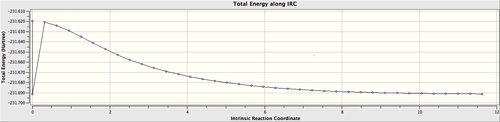
An intrinsic reaction coordinate (IRC) calculation was then set up to calculate the geometry of the chair transition state. This generated a series of stages, by which the bonding in the two allyl fragments changed, and in the process formed a bond in between them. Also generated was a plot of the reaction coordinate of this chair transition state of the cope rearrangement. The sharp dip at the start of the IRC graph appears to be a bug with GaussView, whereby the final structure was generated and then the overall process continued. The gradient of the energy graph flattens to zero towards the right hand side, implying that the reaction has reached completion. As this process has an IRC which is symmetrical about the peak, the direction of reaction was only carried out in the forward direction. The graph showing the gradient of the IRC can be found here. In order to obtain the final structure, a simple HF/3-21G calculation was carried out to minimise the energy of the product molecule.

These calculations and optimisations gave the product shown, which corresponds to the gauche 2 structure. This is demonstrated in the energy similarities, as the gauche 2 structure has an energy of -231.691au, and the graph shown flattens at a very similar value. A video showing the progression of the rearrangement can be found here.

The same method was then used to show the IRC for the boat transition state. The coordinate of this reaction shows a partial minimum, which then decreases in energy further. The reasoning for this can be seen in the video here, in which the same conformation as shown in the chair transition state forms, quickly rearranging to the state shown. The gradient of this reaction coordinate can be found here, from which it can be seen that the gradient reaches approximately zero, and then rises again, before decreasing for a final time. The final product conformation has a total energy of -234.611au (147220.66kcal/mol).

Activation Energies

The energies of the molecules/transition states listed below were then either optimised or re-optimised to a higher level of theory. As can be seen from the data, although the geometries of the molecules optimised are generally indistinguishable, the energies calculated are quite different. The tables below show the differences between these two levels of theory, along with the experimental and calculated activation energies. These calculated activation energies are very close to that measured experimentally, and undoubtedly could be improved using more complex calculations. This, however, would have taken a considerable amount of time. Overall, the values gained were very accurate, and could be reproduced easily.

Energies of Transition States/Products

	HF/3-21G			B3LYP/6-31G*
	Electronic energy(au)	Sum of electronic and zero-point energies(au)	Sum of electronic and thermal energies(au)	Electronic energy(au)	Sum of electronic and zero-point energies(au)	Sum of electronic and thermal energies(au)
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.619	-231.467	-231.461	-233.294	-233.150	-233.145
Boat TS	-231.603	-231.451	-231.445	-234.545	-234.405	-234.398
*Reactant (anti2)*	-231.693	-231.540	-231.533	-234.614	-234.471	-234.464

Calculated Activation Energies

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)(kcal/mol)	45.81	45.18	28.24	26.98	33.5 ± 0.5
ΔE (Boat)(kcal/mol)	55.85	55.22	41.42	41.42	44.7 ± 2.0

The activation energies shown in the table were calculated simply through taking the difference in energy between the starting material and the computationally generated transition state.

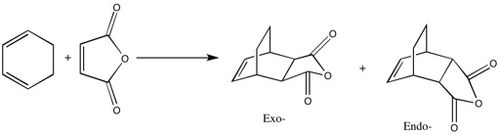
The Diels-Alder Cycloaddition

The Diels-Alder reaction (cycloaddition) is a highly useful tool in organic chemistry, permitting a wide variety of cyclic compounds to be synthesised from relatively simple starting materials. Diels-Alder reactions tend to have a number of common features:

Thermal processes, proceeding in a [4n+2] manner with Hückel transition state
Formation of cyclic (often 6-membered) compounds
Tendency to proceed in a ₄π_s + ₂π_s manner, forming two new σ-bonds at either end of the conjugated systems
Reaction occurs in a concerted manner (pericyclic)

Generally, in these reactions, the Highest Occupied Molecular Orbital (HOMO) of one of the molecules involved interacts with the Lowest Unoccupied Molecular Orbital (LUMO) of the other, creating new bonding and antibonding orbitals in the process. The symmetry of the respective HOMO/LUMO orbitals determines whether the overall reaction will be allowed or forbidden. A very general example of a Diels-Alder cycloaddition can be seen below:

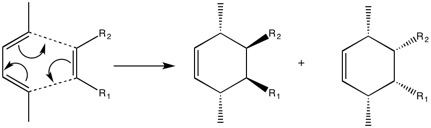
From the reaction scheme, it can be seen that two products are formed: the endo-product on the right hand side, and the exo-product on the left. The relative ratios of these two arrangements depend mainly on the nature of the R groups, however, the endo-product tends to be favoured, leading to the commonly used term: alder-endo rule.
The procedure laid out in the following section details the steps taken to computationally analyse a simple Diels-Alder cycloaddition of a reaction between a molecule of 1,3-Butadiene and another of ethylene.

Building the Reaction

Butadiene

Firstly, a molecule of cis-1,3-butadiene was drawn in GaussView and optimised initially using the HF/3-21G level, and then to the semi-empirical AM1 level. This was then used to generate the HOMO and LUMO of the molecule. It can be seen that the HOMO is antisymmetric with respect to the plane, and the LUMO is symmetric.

Ethylene

A model of ethylene was then created, and the HOMO and LUMO again generated after the same optimisation procedure. From the generated molecular orbitals, it can be seen that the HOMO (π-orbital) is symmetric with respect to the plane, and the LUMO (π*-orbital) is antisymmetric.

From these orbitals, it is clear that the LUMO of butadiene is of the correct symmetry to interact with the HOMO of ethylene, and vice versa. This sets up the alignment of the subsequent Diels-Alder reaction perfectly.

Computing Transition State Geometry

The transition state geometry was set up by drawing a molecule of bicyclo[2,2,2]octane, removing a -CH₂-CH₂- fragment, and breaking the bonds between the 'butadiene' part and the 'ethylene' part.

The freeze coordinate method was used to model the molecular orbitals and vibrational frequencies of the reaction, with the termini of the fragments initially frozen to 2.2Å, before optimising the guess transition state to a minimum. In summary, the following criteria were initially used:

Job Type	Optimise to	Calculate Force Constants	Additional Keywords
Optimize	Minimum	Never	None

This was done to optimise the geometry and energies of the two starting molecules, without changing the distances between the butadiene and ethylene fragments.
The termini of the fragments were once again selected, but rather than freeze coordinates, the derivative option was chosen, and the transition state optimised using the following criteria:

Job Type	Optimise to	Calculate Force Constants	Additional Keywords
Optimize	TS(Berny)	Never	None

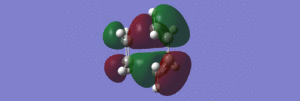
This calculation gave a very good picture of the molecular orbitals of the HOMO of the transition state, which is clearly antisymmetric with respect to the plane (going through the centre of the two molecules). An alternative view of this molecular orbital can be found here. From these pictures, it can be seen that the HOMO of the transition state is the LUMO of the ethylene fragment interacting with the HOMO of the cis-1,3-butadiene fragment. The LUMO is therefore the HOMO of ethylene interacting with the LUMO of butadiene.
This structure had a inter-fragment distance of 2.19Å, and the arrangement and bonding dictates that this is a transition state, as there is a bond forming at the 2-position of the (originally) butadiene molecule. Furthermore, the bond lengths are all approximately 1.38Å, which lies between a double and single bond, signifying a process by which certain bonds are lengthening and others are shortening. The geometry of this transition state can be seen here. Finally, a short video of the imaginary vibrational frequency corresponding to this transition state (at -951.72cm^-1) can be found here. From this movie, it is clear that the ethylene molecule bonds in a concerted fashion to the butadiene molecule, and each end of the molecule bonds to the same side, which proves the theory of syn-addition. This reaction is allowed, according to the Woodward-Hoffman Rules as it occurs with a relatively low electronic energy barrier. Furthermore, the plane of symmetry through the centre of the two molecules (and the product) is conserved, with the HOMO and LUMO of the transition state being antisymmetric and symmetric respectively.
The calculation used to find this vibrational frequency was:

Job Type	Optimise to	Calculate Force Constants	Additional Keywords
Opt+Freq	TS(Berny)	Once	Opt=NoEigen

A number of different strategies were used to find this HOMO - the Opt+Freq strategy detailed here was used, but this generated a molecular orbital, found here, which was completely unrealistic given how relatively simple the starting molecular orbitals were. A similar method, to that detailed here, was also used. This calculation did not work, as the geometries of the reactants and products were not close enough to one another, and this could not be simply ratified. Overall, the calculation detailed above produced a very good view of the molecular orbital, and to a good degree of accuracy.

The bond-forming distances were found to be 2.12Å in this system, which is approximately ⅔ that of double the Van der Waal's radius of carbon (3.40Å). This therefore shows that the two termini are within the distance required for a bond to form between them.

Studying the Regioselectivity of the Diels-Alder Reaction

In this section, the regioselectivity of a specific, substituted Diels-Alder reaction was studied, in order to investigate the relative stability of the endo- and exo- forms. The reaction studied in this section is shown below:

Firstly, the starting compounds (cyclohexa-1,3-diene and maleic anhydride) were drawn and optmised firstly to a HF/3-21G level, and then to a B3LYP/6-31G* level. The frontier molecular orbitals of cyclohexadiene (HOMO, LUMO) and maleic anhydride (HOMO, LUMO) were modeled and a 'guess' transition structure of both the endo- and exo- products was established.

This transition structure was then used to initially model the geometry, vibrations, orbitals and energy of the exo product through utilising the freeze coordinates method used previously. The final optimised structure was then subjected to an opt+freq calculation to show the vibrations leading to the overall reaction. Alternative views of the HOMO and LUMO of this reaction can be found here and here.
The same method was then used to calculate the molecular orbitals for the endo transition state. Alternative views of the HOMO and LUMO can be seen, along with a movie showing the vibration leading to the endo product.

From the vibrations shown, it is clear that the two bonds - between maleic anhydride and cyclohexadiene - form simultaneously (concerted) and due to the reaction occuring with movement of 6 electrons ([4+2]), assuming it is driven by heat, the reaction must occur syn with respect to the fragments (both ends of the alkene bond to the same side of the diene).

The table below shows the relative energies of the two transition states, where it can be seen that the endo form is approximately 4kcal/mol more stabilised than that of the exo form. This stability is in part due to the secondary orbital overlap only seen in the transition state of the endo form. This overlap is between the π*-orbital of the C=O bond of the alkene, and the π-orbital of the C=C in the diene, in the LUMO of the transition state. This can be seen here where the two orbitals are in phase (green on one oxygen, red on the other), leading to stabilising interactions.

Structure	Total Energy(au)	Total Energy(kcal/mol)
Endo	-605.610	-380026.094
Exo	-605.604	-380022.329

A summary of the carbon-carbon bonds that are partially/already formed can be seen below:

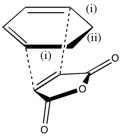
Structure	C-C Length (i) in Cyclohexadiene(Å)	C-C Length (ii) in Cyclohexadiene(Å)	C-C Length in Maleic Anhydride(Å)	Partially Formed C-C Length (Å)
Endo	1.52	1.56	1.48	2.23
Exo	1.52	1.56	1.48	2.26

If these values are compared to normal C-C (1.54Å) and C=C (1.47Å) bonds, it can be seen that they lie in the region of a bond order of 1-2. The bond-forming distance is approximately ⅔ that of double the Van der Waal's radius of carbon (3.40Å), indicating that a bond could feasibly form between these two molecules.

The distances between the -(C=O)-O-(C=O)- fragments and opposite -H₂C-CH₂- (in the exo form) or -HC=CH- (in the endo form) were measured to be 2.92Å and 2.85Å respectively. This indicates that the overall stability of the two forms is a compromise between the greater repulsions of the -HC=CH- orbitals in the endo form and also the stabilising interaction created by the secondary orbital overlap shown in the endo transition state. This is a battle that is clearly won by the the stabilising interaction, given the extra stability of the endo form.
Finally, the exo form is likely to be more strained than the endo form due to the -(C=O)-O-(C=O)- being closer to the bridging carbons in the exo form than the same fragment is to the -HC=CH- bond in the endo form (2.92Å compared to 2.99Å). This is potentially a final factor leading to the endo form being of a more stable geometry than the exo form.

References

↑ An analysis of the conformers of 1,5-hexadiene BRANDON G. ROCQUE, JASON M. GONZALES, HENRY F. SCHAEFER Molecular Physics Vol. 100, Iss. 4, 2002
↑ Conformational Study of 1,5-Hexadiene and 1,5-Diene-3,4-diols Benjamin W. Gung, Zhaohai Zhu, and Rebecca A. Fouch Journal of the American Chemical Society 1995 117 (6), 1783-1788
↑ M.J. Bearpark https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3#The_Cope_Rearrangement_Tutorial [accessed 22/10/2013]
↑ M.J. Bearpark https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3#The_Cope_Rearrangement_Tutorial [accessed 22/10/2013]

[1] An analysis of the conformers of 1,5-hexadiene BRANDON G. ROCQUE, JASON M. GONZALES, HENRY F. SCHAEFER Molecular Physics Vol. 100, Iss. 4, 2002

[2] Conformational Study of 1,5-Hexadiene and 1,5-Diene-3,4-diols Benjamin W. Gung, Zhaohai Zhu, and Rebecca A. Fouch Journal of the American Chemical Society 1995 117 (6), 1783-1788

[3] M.J. Bearpark https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3#The_Cope_Rearrangement_Tutorial [accessed 22/10/2013]

[4] M.J. Bearpark https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3#The_Cope_Rearrangement_Tutorial [accessed 22/10/2013]

[1]

[2]

[3]

[4]