THE COPE REARRANGEMENT

Jonathan Shute

Introduction / Background Theory

This report aims to investigate the thermochemistry of the following reaction:

It is understood that the reaction occurs in a concerted fashion via either chair or boat like transition state:

In the tutorial section, the enthalpy of the reactant has been found when it is in its most energetically stable conformer. In the second part, the chair and boat transition geometries have been located and their energies calcualted. These data were then used to calculate the activation energy of the reaction.

Several methods were employed to obtain the transition states. Every transition state has with it associated one imaginary frequency. This is because bonds can be modelled as vibrational springs obeying Hooke's law, F= -kx. The frequencies are computed using the following equation:

$\frac{1}{2 π} \sqrt{\frac{k}{μ}} .$

The force constants are negative at the transition state so the frequency is imaginary.

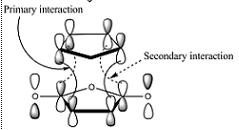
In the project, Diels-Alder reactions were investigated. In the diels alder reaction, the endo product is formed preferentially despite being the less thermodynamically stable product. (It suffers more from sterics). The reaction is consequently under kinetic control and the stereoselectivity can be explained by invoking the secondary orbital effect which stabilises the transition state and so lowers the activation energy for formation of the exo product which forms faster. In the project, the orbitals involved with this effect were computed and studied.

Optimising the Reactants and Products

1,5-hexadiene

(a)The energy of the anti conformer is -231.6926(0235) a.u and the symmetry is C1 File:Hexatriene anti optimised 321Gjs.log

(b)The energy of the gauche conformer is -231.6915(30325) File:HEXATRIENEGAUGEjs 321G.LOG

The gauche conformer is slightly higher in energy due to the carbons 1 and 4 of the central carbons eclipsing each other a little and causing steric repulsion whist in the staggered conformation, there is less interaction between them. In the antiperiplaner conformation, there is overlap between the sigma C-C bonding orbital for carbons C1 and C2 and the C-C antibonding orbital between C3 and C4. This lowers the energy slightly.

In both structures, A1,3 eclipsed conformation ^[1] is evident with the H atoms on the carbon adjacent to C=C at roughly 120o to the pi system, although not exactly and in both structures one of the H's is at a slightly larger angle than this. The A1,3 conformation is a compromise between having two hydrogen's sigma orbitals aligned fairly well with the pi star orbitals and also there is an attractive vdw force between the H atom on the C=C and on the H atom on the neighbouring carbon. The distance is slightly larger in the gauche.

These orbitals show interaction of the sigma H orbital with the pi star orbitals is effective for both conformers.

(c) The lowest energy conformers of 1,5-hexadiene in the table are anti1 and gauche3

(d)By comparison with the appendix table, my optimised conformers were anti1 and gauche4. [My Optimisation Summary Table]

(e)The optimised molecule had point group Ci and an energy matching the value given in appendix of -231.69253528 a.u precisely. File:TRIAL2VER2 321G.LOG

 Low frequencies ---   -5.6849   -2.3517   -2.0910   -0.0008   -0.0004   -0.0002
 Low frequencies ---   71.1980   85.6851  116.1458

 Zero-point correction=                           0.152996 (Hartree/Particle)
 Thermal correction to Energy=                    0.159970
 Thermal correction to Enthalpy=                  0.160914
 Thermal correction to Gibbs Free Energy=         0.121620
 Sum of electronic and zero-point Energies=           -231.539539
 Sum of electronic and thermal Energies=              -231.532565
 Sum of electronic and thermal Enthalpies=            -231.531621
 Sum of electronic and thermal Free Energies=         -231.570916

This gives an electronic energy of 231.692535 (by subtracting the zero point correction to the sum of electronic and zero point energies).

All is in close agreement with the appendix table (only variation in the sixth decimal place)

(f)The conformation of the molecule appears the same when both basis sets are used though the C=C bond length is a little longer with the better basis set at 1.333 A compared to 1.316 A. The energy is very significantly different at -234.611706. This is why the energy of different molecules can only be compared if it was computed with the same basis set. File:HEXATRIENEANIT2CI 631GD.LOG File:HEXATRIENEANIT2CI 631GD FREQCHECKjs.LOG

''' Low frequencies ---   -9.1026    0.0005    0.0005    0.0008    4.2776   13.4006
 Low frequencies ---   74.2705   80.9525  121.5200

Zero-point correction=                           0.142504 (Hartree/Particle)
 Thermal correction to Energy=                    0.149851
 Thermal correction to Enthalpy=                  0.150795
 Thermal correction to Gibbs Free Energy=         0.110929


 Sum of electronic and zero-point Energies=           -234.469207
 Sum of electronic and thermal Energies=              -234.461859
 Sum of electronic and thermal Enthalpies=            -234.460915
 Sum of electronic and thermal Free Energies=         -234.500782

(It is a little surprising that the low frequencies are higher for the optimisation with the better basis set)

Optimising Chair and Boat Transitions

(b)

 
 Low frequencies --- -817.9271   -7.0897   -5.4674   -4.3204   -0.0004    0.0004
 Low frequencies ---    0.0005  209.4156  396.0571
 ******    1 imaginary frequencies (negative Signs) ******

DOI:10042/21119 (optimised log file of chair guessed transition state)

 Zero-point correction=                           0.152627 (Hartree/Particle)
 Thermal correction to Energy=                    0.157986
 Thermal correction to Enthalpy=                  0.158930
 Thermal correction to Gibbs Free Energy=         0.124120
 Sum of electronic and zero-point Energies=           -231.466696
 Sum of electronic and thermal Energies=              -231.461336
 Sum of electronic and thermal Enthalpies=            -231.460392
 Sum of electronic and thermal Free Energies=         -231.495202

These results agree with those given in the appendix with variation in fifth d.p only.

(c)

File:INCORRRECTjs.LOG

(d)File:CORRRECTED OPTIMISE TOA TRANSITION STATE.LOGOptimisation to a transition state was successful but initially failed until write connectivity was unchecked under the general tab. The bond lengths were 2.01995 A. This is corroborated by the results for the optimised chair in part (b) which gave a bond length of 2.0205 remarkably similar considering the differences in the models used.

Zero-point correction=                           0.151377 (Hartree/Particle)
 Thermal correction to Energy=                    0.157016
 Thermal correction to Enthalpy=                  0.157960
 Thermal correction to Gibbs Free Energy=         0.122592
 Sum of electronic and zero-point Energies=           -231.463821
 Sum of electronic and thermal Energies=              -231.458181
 Sum of electronic and thermal Enthalpies=            -231.457237
 Sum of electronic and thermal Free Energies=         -231.492605

-231.619322 -231.466705 -231.461346

(e) File:GAUGE TS(QST2)ERRDEFAULTSPIN.LOG successful optimisation with 2.140 bond length. Only one imaginary frequency (which is vibration of the two bonds which are forming):

Animation supposed to show vibrations at ts


 Low frequencies --- -840.1011   -4.0811   -0.0011   -0.0010   -0.0009    3.5285
 Low frequencies ---    5.2099  155.3480  382.0830
 ******    1 imaginary frequencies (negative Signs) ******

 Zero-point correction=                           0.151874 (Hartree/Particle)
 Thermal correction to Energy=                    0.157502
 Thermal correction to Enthalpy=                  0.158447
 Thermal correction to Gibbs Free Energy=         0.123029
 Sum of electronic and zero-point Energies=           -231.450929
 Sum of electronic and thermal Energies=              -231.445300
 Sum of electronic and thermal Enthalpies=            -231.444356
 Sum of electronic and thermal Free Energies=         -231.479774

These results are very close to those in the appendix table for 321G HF basis set and method.

(f) DOI:10042/21197 file shows the IRC on the chair transition state calculated using redundant method.

(g) (Initially the boat was optimised to the HF/6-31G* level accidently. These results are included any way under the extra working section) The calculation below is with the correct method.

i) Correct method

DOI:10042/21294

 Zero-point correction=                           0.140741 (Hartree/Particle)
 Thermal correction to Energy=                    0.147079
 Thermal correction to Enthalpy=                  0.148023
 Thermal correction to Gibbs Free Energy=         0.111326
 Sum of electronic and zero-point Energies=           -234.402355
 Sum of electronic and thermal Energies=              -234.396016
 Sum of electronic and thermal Enthalpies=            -234.395072
 Sum of electronic and thermal Free Energies=         -234.431769

There is a small variation when compared to appendix values in the fifth d.p.

ii) DOI:10042/21304 DOI:10042/21305 Reoptimised the chair calculated in part b to B3YLP/6-31G* level:

 Zero-point correction=                           0.142054 (Hartree/Particle)
 Thermal correction to Energy=                    0.147975
 Thermal correction to Enthalpy=                  0.148919
 Thermal correction to Gibbs Free Energy=         0.113168
 Sum of electronic and zero-point Energies=           -234.414929
 Sum of electronic and thermal Energies=              -234.409008
 Sum of electronic and thermal Enthalpies=            -234.408064
 Sum of electronic and thermal Free Energies=         -234.443815

Again, these results are in close agreement with those in the appendix table to the fifth d.p

Conclusion

The energy of the chair minus the thermal correction is -234.557 a.u. The energy of the reactant is -234.612 a.u Need to subtract energy of starting materials and reactants to give the extra energy of the transition state which must be overcome for reaction to occur. 1 Hartree = 627.509 kcal/mol

Hence, the difference in energy is -5.471*10^-2. This is 34.3 kcal mol-1.

The energy of the boat is -234.543 a.u. This gives Ea = 0.0689 a.u or 43.2 kcal mol-1

These values compare to the literature values of 33.5 ± 0.5 kcal/mol via the chair transition structure and 44.7 ± 2.0 kcal/mol via the boat transition structure. This is surprisingly good agreement as the basis set used B3LYP/6-31G* is quite an inexact basis set.

Extra Working

Initially the boat was optimised to the HF/6-31G* level accidently. These results are included any way below as an extension to the tutorial!

(g) DOI:10042/21218 this is the optimised boat HF/3-21G reoptimised file is IRC_chair_redundant. The results are given below:

Low frequencies --- -852.3991   -6.1132   -4.0906   -1.4954   -0.0005    0.0006
 Low frequencies ---    0.0007  145.9558  320.2847
 ******    1 imaginary frequencies (negative Signs) ******

Zero-point correction=                           0.150402 (Hartree/Particle)
 Thermal correction to Energy=                    0.156295
 Thermal correction to Enthalpy=                  0.157239
 Thermal correction to Gibbs Free Energy=         0.121318
 Sum of electronic and zero-point Energies=           -232.727993
 Sum of electronic and thermal Energies=              -232.722099
 Sum of electronic and thermal Enthalpies=            -232.721155
 Sum of electronic and thermal Free Energies=         -232.757076

The optimisation at the HF/6-31G* level reached a minimum with the energy derivatives very close to zero after the eighth step (smaller than 10^-4) however due to an error in the program (unstable algorithm) it continued beyond this point and the final structure was incorrect. The eighth intermediate geometry has a bond length of 2.203 A. The following link is to screenshots of the optimisation graphs and the energy derivatives: [Optimisation_Graphs]

DIELS ALDER PROJECT

Results

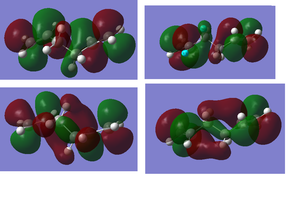
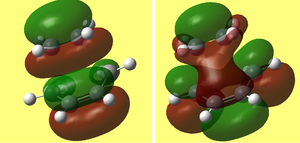
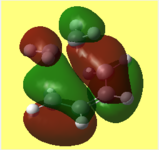
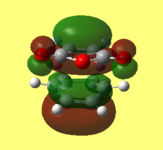
i) This is my diagram of the LUMO left and the HOMO right. The LUMO is antisymmetric with respect to the plane and the HOMO is symmetric.

ii)Optimisation using method in part b) (HF/321G) file = partA_RETRY in folder ii)

The animation clearly shows the correct transition state has been attained.

Vibration

The animation is supposed to show concerted bond formation.

 Low frequencies --- -818.4961   -0.0007   -0.0006   -0.0003    1.4348    1.8772
 Low frequencies ---    2.7185  166.5539  284.3675
 ******    1 imaginary frequencies (negative Signs) ******

Zero-point correction=                           0.151870 (Hartree/Particle)
 Thermal correction to Energy=                    0.157558
 Thermal correction to Enthalpy=                  0.158502
 Thermal correction to Gibbs Free Energy=         0.122930
 Sum of electronic and zero-point Energies=           -231.451338
 Sum of electronic and thermal Energies=              -231.445650
 Sum of electronic and thermal Enthalpies=            -231.444706
 Sum of electronic and thermal Free Energies=         -231.480279

iii) Exo Transition States DOI:10042/21391 This is the file for my optimised exo transition state calculated using the derivatise bond method. I also calculated the transition state using the first method in the tutorial section

Modredundant method: 99_frozengif is the input file, output log is 99_99_99 DOI:10042/21447

 Low frequencies --- -643.0720  -10.8719   -0.0008   -0.0008   -0.0004   11.9743
 Low frequencies ---   15.1280   49.8386  133.6533
 ******    1 imaginary frequencies (negative Signs) ******

Zero-point correction=                           0.195473 (Hartree/Particle)
 Thermal correction to Energy=                    0.204891
 Thermal correction to Enthalpy=                  0.205835
 Thermal correction to Gibbs Free Energy=         0.160107
 Sum of electronic and zero-point Energies=           -605.408011
 Sum of electronic and thermal Energies=              -605.398593
 Sum of electronic and thermal Enthalpies=            -605.397649
 Sum of electronic and thermal Free Energies=         -605.443378

Opt=NoEigen method: DOI:10042/21449


Low frequencies --- -647.3174   -2.2007   -0.0010   -0.0009   -0.0008    1.7640
 Low frequencies ---    3.1286   42.6020  131.4691
 ******    1 imaginary frequencies (negative Signs) ******

 Zero-point correction=                           0.195451 (Hartree/Particle)
 Thermal correction to Energy=                    0.204911
 Thermal correction to Enthalpy=                  0.205855
 Thermal correction to Gibbs Free Energy=         0.159905
 Sum of electronic and zero-point Energies=           -605.408140
 Sum of electronic and thermal Energies=              -605.398681
 Sum of electronic and thermal Enthalpies=            -605.397736
 Sum of electronic and thermal Free Energies=         -605.443686

methodA = 9999log.... file ? Note some disagreement in the transition state optimal distance! Could also include guess file?

The endo transition state: DSPACE LINK TO include. Fies are endo_optimise_ts_A_take2 and log_65019

I optimised this using the opt=noeigen method and the modredundant method to check. First I drew a guess transition state by drawing the product, optimising it to a minimum and then increasing the bond forming lengths to 2.2A The energies are given below and are in good agreement for the different methods. The transition state geometries are very similar for both, with C-C bond forming distances of 2.231 with both methods which agree to the third decimal place.

Calculation using opt=noeigen key word: DOI:10042/21451 Optimisation Summary Table

 Low frequencies --- -643.5783   -0.0005   -0.0002    0.0006    0.6895    1.1675
 Low frequencies ---    1.7996   65.0129  142.0450
 ******    1 imaginary frequencies (negative Signs) ******

 Zero-point correction=                           0.195464 (Hartree/Particle)
 Thermal correction to Energy=                    0.204889
 Thermal correction to Enthalpy=                  0.205834
 Thermal correction to Gibbs Free Energy=         0.160235
 Sum of electronic and zero-point Energies=           -605.414905
 Sum of electronic and thermal Energies=              -605.405479
 Sum of electronic and thermal Enthalpies=            -605.404535
 Sum of electronic and thermal Free Energies=         -605.450133

Calculation using modredundant keyword: DOI:10042/21452 Optimisation Summary Table

Low frequencies --- -644.2611   -0.0007   -0.0003    0.0006    1.8423    3.3886
 Low frequencies ---    6.6938   65.0647  142.3913
 ******    1 imaginary frequencies (negative Signs) ******

Zero-point correction=                           0.195454 (Hartree/Particle)
 Thermal correction to Energy=                    0.204879
 Thermal correction to Enthalpy=                  0.205823
 Thermal correction to Gibbs Free Energy=         0.160231
 Sum of electronic and zero-point Energies=           -605.414912
 Sum of electronic and thermal Energies=              -605.405487
 Sum of electronic and thermal Enthalpies=            -605.404543
 Sum of electronic and thermal Free Energies=         -605.450135

Bond formation is concerted

Discussion Questions

1) This is my diagram of the LUMO left and the HOMO right. The LUMO is antisymmetric with respect to the plane and the HOMO is symmetric.

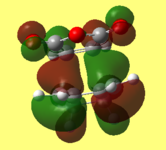
2) Below is illustrated the HOMO left and LUMO right for the unsubsituted Diels Alder transitions state. Both orbitals are symmetric with respect to the plane.

These diagrams show the orbital contributions of the MOs above them.

The HOMO has a node in between the diene and the dienophile.

Allowed reactions: The reaction is allowed by Woodward-Hoffmann rules as there are six electrons, it is suprafacial and a thermal process. Frontier orbital theory predicts the stereochemistry. As two new bonds are being formed simultaneously, there are symmetry constraints on the reaction. If both p orbitals on the alkene form constructive overlap with the p orbitals on the terminal carbons of the diene, then the reaction is allowed.

In the HOMO the alkene and diene both have the same symmetry and interact to strengthen the bonds which are forming. (Both components have no nodes)and both components are symmetric

In the HOMO-1, both components have the same symmetry for overlap and this strengthens the two bonds which are forming both components are antisymmetric

The LUMO is interesting because the two components are symmetric and they have to correct symmetry to interact however they do so destructively and so weaken the 2 bonds which are forming. However, the orbitals deform and the p orbitals on the alkene balloon out to interact with the p orbitals on the central two carbons of the diene so this would cause a little weak bonding between these atoms.

A further point to make is that the HOMO-1 is the key MO as it has strong positive overlap inbetween the diene and dienophile and so is the major bonding attraction which causes the transition state to roll onto the products. This is because electrons inhabiting this low energy orbital attract the two fragments together.

In the transition state, the HOMO-1 is made up of the LUMO of ethene and the HOMO of the diene A "real" Diels Alder reaction requires an electron deficient dienophile and this lowers the energy of its LUMO whilst the diene has a high energy HOMO so the interactions of this orbital are strengthened even more. In reverse demand reactions the following interaction is preferred:

3)

Bond forming distance: 2.209 A. According to a table on wikipedia ^[2], the average bond lengths are as follows: sp2-sp2 C-C = 1.47 A (BUT the alkene double bond length according to the same table is 1.34A Gaussview gives the bond length in ethene of 1.325) sp3-sp3 C-C = 1.54 A (gaussview has 1.5 for ethane) sp3-sp2 C-C = 1.50 A longest C-C = 1.74 A Additionally, the Van der Waals radius for carbon is 1.7 A ^[3]

The reason that bond lengths are less than the corrosponding average of the radii of the two atoms is that their electron clouds overlap when forming the bond so the nuclei are draw in towards each other somewhat. Two carbon atoms can't form a normal covalent bond in their distance exceeds the van der waals radius. There may be some intermolecular attraction but there isn't a bond. There will be some overlap between the sigma orbitals but it must be weak at this distance. It might have been expected that the length would be upwards from the average of the vdw radius distance and that of a normal sp3 C bond which would be 1.6A but the distance is much more than this.

This, along with the other bond lengths implies that the transition state is "reactant like" i.e. an early transition state. The dienophile has a C=C bond length of 1.375 which is far closer to the double bond length than the single bond length. The dienophile has two bond lengths of 1.39 and two of 1.37 whilst these are all quite short, this also implies that the transition state is at least somewhat more reactant like than product like.

This synchronous vibration compares to the asynchronous one below (however this vibration has sideways motion as well as asynchronous in and out motion).

(This is actually the second lowest positive frequency but the lowest one doesn't show the two molecules moving closer or further apart, only moving sideways relative to each other)

Substituted Diels Alder

4) The exo transition state is a slighlty more strained as the maleic anhydride componant points towards the bridging carbons. The Oxygen atoms are a little closer to the hydrogens which are on sp3 carbons and so jut out more than the nearest hydrogens on sp2 like carbon to the maleic anhydride component in the endo. This is in part due to the fact that the transition state appears more product like in the endo and more reactant like in the exo. In the actual products, this affect may be extenuated as in the endo transition state, the maleic anhydride oxygen atoms are pulled closer to the C=C to increase secondary orbital overlap.

5) The endo transition state has energy = -605.610 a.u. The exo transition structure has energy -605.603 a.u this gives a difference of 4.4 kcal mol-1.

This is the HOMO-1 in the endo transition state showing positive overlap between the orbitals on the oxygen atoms and the C=C

This shows the HOMO. (There is a node between the p on the oxygen atoms and the diene showing that in the HOMO, the endo could be slightly destabilised by this interaction. In the HOMO-1 shown above, there is constructive overlap between the oxygen atoms and the rest of the molecule - though any interaction atall is very weak)

According to the theory ^[4] ,the secondary orbital overlap is caused by the interation between the pi star C=O and the C=C. However, it is the p on C which interacts, not the p on oxygen which is too far out:

However, in my HOMO, it appears that the p on C doesn't contribute unless its been "swallowed up" into the nearby p orbitals on the other C atoms.

6) Factors neglected in the calculation of the transition states: In order for the reactants to react via the exo or endo transition state, an exact alignment is required so there is a high entropy barrier to overcome but if the two components misalign, they are weakly attracted and can move relative to each other until the correct alignment is attained. This means the energy of the transition states may be less high than calculated.

References

↑ Second year lecture course, "conformational analysis" by Dr Rzepa http://vle.imperial.ac.uk/webct/cobaltMainFrame.dowebct
↑ http://en.wikipedia.org/wiki/Bond_length
↑ http://en.wikipedia.org/wiki/Van_der_Waals_radius
↑ http://en.wikipedia.org/wiki/Frontier_molecular_orbital_theory

[Rzep-1] Second year lecture course, "conformational analysis" by Dr Rzepa http://vle.imperial.ac.uk/webct/cobaltMainFrame.dowebct

[wikibondlength-2] ttp://en.wikipedia.org/wiki/Bond_length

[wikivdw-3] ttp://en.wikipedia.org/wiki/Van_der_Waals_radius

[wikifrontier-4] ttp://en.wikipedia.org/wiki/Frontier_molecular_orbital_theory

[1]

[2]

[3]

[4]