Rep:Mod:JOH95

Introduction

Transition states represent molecules between the reactants and products. If the transition state resembles the products, it is known as an early transition state; if the transition state resembles the reactant, it is known as a late transition state. A transition state represents the highest energy along a reaction coordinate and is highly unstable. Transition state structures cannot be isolated in organic synthesis but can be computationally calculated to a high degree. Computational programs, such as GaussianView, can solve the Schrodinger equation, $\hat{H}\mathrm{\Psi }=E\mathrm{\Psi }$, to give an accurate model for transition states structures. The Hamiltonian operator is calculated using Semi-Empirical Methods (AM1), Hartree-Fock methods (HF) or Density Functional Theory (DFT). Semi-Empirical Methods use multiple approximations to calculate the Hamiltonian operator and so are only used as a rough guide when working out transition states. Hartree-Fock is a better approximation and takes into account the kinetic energy of the electrons, the electron-nuclei interactions and the coulomb interactions between electrons. Density Function Theory takes one further step and also includes the exchange-correlation potential due to spin and charge. In this experiment, Hartree-Fock calculations will be mainly used as it provides enough information to model transition states without being too approximate or too time consuming to calculate.

Nf710 (talk) 18:53, 21 January 2016 (UTC) HF uses a single slater determinant of all electronic configurations to satify the pauli exclusion priniciple. DFT uses a hamaltonian with a function of the electron density.

When calculating the Hamiltonian operator using HF or DFT the orbital interactions need to be modelled by choosing a basis set. The double-zeta basis set treats each orbital separately when conducting Hartree-Fock calculations. Each atomic orbital must be expressed as a sum of two Slater-type orbitals (STOs). The two equations are the same apart from zeta, which accounts for how diffuse the orbital is. The constant $d$ determines how much each STO will count to the final orbital.

For example the equation for a 2s orbital is given:

${\mathrm{\Phi }}_{2s}$(r) = ${\mathrm{\Phi }}_{2s}^{STO}$(r, ${\zeta }_1$) + d${\mathrm{\Phi }}_{2s}^{STO}$(r, ${\zeta }_2$)

The linear combination of these STOs gives the atomic orbital. The triple and quadruple basis set works in the same way except they use three and four Slater equations but the better accuracy requires more time to calculate.

Calculating a double-zeta basis set on all orbitals can take too long. Split-valence basis set calculates two Slater equations for only the valence orbitals and one Slater equation for the inner orbitals. This method is more approximate but requires less time to calculate. We will mainly be using 3-21G as a basis set.

1. The 3 is the number of Gaussian functions describing the inner shell orbitals
2. The 2 is the number of Gaussian functions that comprise the first STO of the double zeta
3. The 1 is the number of Gaussian functions summed in the second STO.

The 3-21G basis set treat atomic orbitals as existing as only s, p, d etc. This does not take into account how these orbitals change when they interact and that orbitals may possess s and p character for example. This interaction takes into account of the polarisation effect and one asterisk is used to show that polarisation has been taken into account in the ‘p’ orbitals. For example, the difference between 6-31G and 6-31G* is that the p orbital possess dz2 character. In this computational experiment 6-31G* will be used as a basis set for more accurate calculations.

AM1 calculations do not use a basis set as the orbital interactions are implied in the calculation.

Nf710 (talk) 18:55, 21 January 2016 (UTC) Very in depth explanation of bais sets well done

The Cope Rearrangement of 1,5-Hexadiene

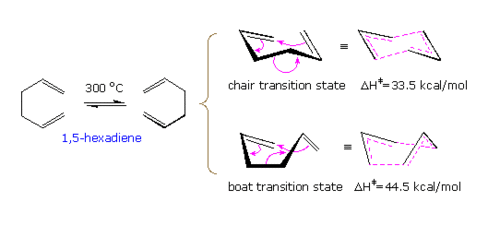
Fig1. The Cope Rearrangement with its transition states

The Cope Rearrangement involves a [3,3]-sigmatropic shift rearrangement - the mechanisms of which are either through a chair or boat transition as shown above. The boat transition structure is higher in energy. Using the B3LYP/6-31G* method, accurate activation energies can be calculated

Optimisation of 1,5-hexadiene Conformers

Anti1 Conformer of 1,5-hexadiene

Using GaussView, 1,5-hexadiene was drawn with an anti peri planar conformation. This was achieved by setting the dihedral angle to 180^o. Once the structure was cleaned it was optimized at the HF/3-216 level of theory. The Point Group Symmetry was C₂.

Gauche Conformer of 1,5-hexadiene

The same method was applied but with the dihedral angle set to 60^o. When optimized, the gauche conformer was not the lowest possible conformer so the dihedral angle was adjusted to 67^o. When optimized this gave the lowest possible gauche conformer. The Point Group Symmetry was C₁.

Anti2 Conformer of 1,5-hexadiene

The anti conformer with C_i point group symmetry was drawn using the HF/3-216 level of theory. The molecule was then re-optimized using B3LYP/6-31G*.

Comparison of 1,5-hexadiene Conformers

Conformer	Structure	Level of theory	Point Group	Energy/Hartrees	Relative Energy/kcal/mol	Log file
anti1		HF/3-21G	C2	-231.69260	0.04	anti1
gauche		HF/3-21G	C1	-231.69266	0.00	gauche
anti2		HF/3-21G	Ci	-231.69254	0.08	anti2
anti2		B3LYP/6-31G*	Ci	-234.61171	n/a	anti2

Nf710 (talk) 18:59, 21 January 2016 (UTC) Excellent use of jmols

Comparison of lowest energy conformers

The anti2 conformer is expected to have the lowest energy because the molecule appears less sterically hindered when compared to the gauche form . However, it can be seen in the table above that the gauche has the lowest relative energy. This is explained by secondary orbital overlap. The gauche conformer has more secondary orbital overlap compared to the anti2 conformer, therefore it is more stable.

Fig2. Anti2 secondary orbital overlap

Fig3. gauche secondary orbital overlap

Nf710 (talk) 19:00, 21 January 2016 (UTC) Excellent use of the orbitals to show the rlatige energies

Comparison of anti2 levels of theory

The anti2 conformer was optimized using two levels of theory. The B3LYP/G-31G* is a higher level of theory so should give a more accurate results. Whilst the energies of the two molecules can not be compared as they use different levels of theory the bond lengths and angles can be compared.

Figure 4. Anti2 labelled structure

Atoms	HF/3-21G/ Å	B3LYP/6-31G*/ Å	Increase/Decrease
C6-C4	1.31618	1.33350	Increase
C4-C1	1.50882	1.50420	Decrease
C1-C14	1.55317	1.54816	Decrease

The dihedral angles were also compared to see how the B3LYP/6-31G* optimization affected the molecule compared to a HF/3-21G optimization.

Atoms	HF/3-21G/ 0C	B3LYP/6-31G*/ 0C	Increase/Decrease
C6-C4-C1-C14	114.62608	118.59950	Increase
C4-C1-C14-C12	180.00000	180.00000	No change
C1-C14-C12-C9	114.62608	118.59950	Increase

It appears that as you move from using HF/3-21G to using B3LYP/6-31G* the double bond lengths increase and the single bond lengths decrease. The increase in double bond lengths and decrease in single bond lengths indicate that the higher level of theory is taking into account the delocalisation of the double bonds into the single bond, hence why the C6-C4 have less double bond character and C4-C1 have less single bond character.

Frequency analysis on anti2 conformer

A frequency calculation was run on the B3LYP/6-31G* optimized anti2 conformer in order to measure the energies and frequencies of the conformer. There was no imaginary vibration, as expected. The log file can be found here.

Figure 5. The IR spectrum of the Anti2 conformer

Different energies were calculated in the frequency calculation:

1. The energy at 0 K including zero-point vibrational energy (E = E_elec + ZPE)
2. The energy at 298.15 K and 1 atm of pressure which includes contributions from the translational, rotational, and vibrational energy modes (E = E + E_vib + E_rot + E_trans)
3. The energy including an additional correction for RT (H = E + RT)
4. The energy including the entropic contribution to the free energy (G = H - TS)

Energetic Values	B3LYP/6-31G*
Sum of Electronic and Zero-point Energies at 0 K	-234.469219
Sum of Electronic and Thermal Energies at 298.15 K	-234.461869
Sum of Electronic and Thermal Enthalpies	-234.460925
Sum of Electronic and Thermal Free Energies	-234.500809

Optimization of boat and chair transition states

The transition structure optimizations will be performed on chair and boat structures by:

1. Using Force constants
2. Using redundant coordinate editor
3. Using QST2

The Intrinsic Reaction Coordinate will be performed and activation energies will be calculated

Allyl fragment optimization

The allyl fragment was drawn, cleaned and optimized using HF/3-21G.

Conformer	Structure	Level of theory	Point Group	Energy/Hartrees	Log file
allyl fragment		HF/3-21G	C2v	-115.82304010	log file

Optimization to a TS (Berny)

Two of these fragments were put together to create the transition state structure for the Cope rearrangement. The method to obtain the transition state was as follows:

1. The distance between the two fragments was set 2.2 Å apart as a guess for the transition structure.
2. An Opt+Freq calculation was performed on the guess transition state structure and it was optimizes to a TS (Berny)
3. The force constant was changed to Once and an addition description of Opt=NoEigen was added to prevent the calculation crashing if more than one imaginary frequency was detected.

The vibration spectrum of the transition state will have one imaginary frequency which means that the energy has a maximum where all other energies are at a minimum. An imaginary transition state frequency is formed from a negative force constant. Through analysis of the equation below, it can be seen that if the force constant ($k$) is negative then a square root of a negative, and thus an imaginary number, is included in the frequency.

$E_n=h(n+\frac{1}{2})\nu =h(n+\frac{1}{2})\frac{1}{2\pi }\sqrt{\frac{k}{m}}$,

The results of the optimization are shown below.

Conformer	Method	Structure	Level of theory	Energy/Hartrees	Imaginary frequency/ cm-1	Log file
Chair	Berny method		HF/3-21G	-231.61932219	-817.94	log file

Optimizing a transition state using the Frozen Coordinate Method

Optimizing a transition state by guessing the structure can be problematic. In order to help with this problem, different parts of the molecule can be optimized separately in order to obtain a guess structure closer to the transition state. The method is as follows:

1. The allyl fragments were frozen 2.2 Å apart
2. The terminal carbons were optimized separately to a minimum
3. The bond forming/breaking distances fixed to 2.2 Å were then optimized
4. Then a transition state optimization was performed

The results can be seen in the table below

Conformer	Method	Structure	Level of theory	Energy/ Hartrees	Imaginary frequency/ cm-1	Log file
Chair	Freeze coordinate method		HF/3-21G	-231.61992412	-817.95	log file

QST2 method

The boat transition structure was optimized using the QST2 method. This method calculates the transition structure between reactant and products. The reactants and products must be manually labelled so that the atoms remain in the same position, as shown in figure 6.

The first attempt for finding the transition state was as follows:

1. The anti2 optimized structure was copied and pasted to a new window
2. In this window a new MolGroup was added
3. The anti2 optimized structure was copied into this new window
4. The product molecule was labelled to match that of the reactant molecule as shown in figure 6
5. Opt+Freq calculation was run and TS(QST2) was selected

Fig6. Labelling of products and reactants

This optimization gave an unexpected transition state, as shown in figure 7, as the calculation had not considered bond rotation

Fig7. First attempt transition state

The original input file was modified to prevent this unexpected transition state. The dihedral angle were set to 0^o and the inside carbon bond angles were reduced to 100^o. The QST2 calculation was run again to give the transition state. The results of this optimization can be seen in the table below.

Fig8. Re-arrangement of products and reactants

Conformer	Method	Structure	Level of theory	Energy/ Hartrees	Imaginary frequency/ cm-1	Log file
Boat	QST2		HF/3-21G	-231.60280242	-840.07	log file

IRC Calculation

The Intrinsic Reaction Coordinate (IRC) calculation finds a local minimum from a transition state by following a minimum energy path along a potential energy surface. The structure found in the IRC can show which conformer that the transition state is made from. The local minimum structure will be more accurate if a higher the number of points are considered but it is unnecessary to run steps once the RMS gradient norm plateaus at 0.

The IRC was calculated for the first chair structure calculated. The method for running the IRC was as follows:

1. IRC was selected as the Job
2. The reaction coordinate was calculated in the forward direction
3. The force constant was calculated always
4. The number of points along the IRC was chosen to be 50

The results of the IRC are are in figure 9 and 10 and the log file can be found here.

Fig9. Total energy along IRC

Fig10. RMS gradient norm along IRC

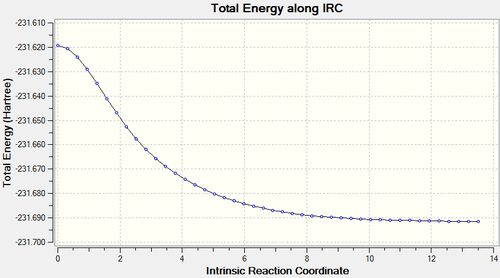
The local minimum structure was found, as shown in figure 11, and had an energy of -231.69157839 a.u.

Fig11. Local minimum structure

Nf710 (talk) 19:14, 21 January 2016 (UTC) if you would have optimised this down you wuld have seen that it would have gone to the gauche 2 energy.

Comparing 3-21G and 6-31G*

The chair and boat were re-optimized using B3LYP/6-31G* level of theory by starting from the HF/3-21G structures. The log files for the re-optimized B3LYP/6-31G* chair can be found here and the boat here.

The structures were compared and shown to be similar.

	Bond forming lengths (Å)
	HF/3-21G	B3LYP/6-31G
Chair TS	2.01978	1.96755
Boat TS	2.13993	2.20705

The energies however were found to be very different

Summary of energies (in hartree)

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.619322	-231.466697	-231.461338	-234.556983	-234.414929	-234.409009
Boat TS	-231.602802	-231.450928	-231.445299	-234.543079	-234.402360	-234.396016
Reactant (anti2)	-231.692535	-231.539539	-231.532566	-234.611711	-234.469219	-234.461869

*1 hartree = 627.509 kcal/mol

Summary of activation energies (in kcal/mol)

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.71	44.70	34.07	33.17	33.5 ± 0.5
ΔE (Boat)	55.60	54.76	41.95	41.32	44.7 ± 2.0

This shows the lower basis set is good at calculating correct geometries but not good at calculating energies which is achieved using a higher level of theory.

Nf710 (talk) 19:17, 21 January 2016 (UTC) In general this is a very good report, you have shown a good understanding of the methods, you have used jmols excellently and it is formatted excellently. You have done everything asked of you can you have gone beyond the script to learn about basis sets

Diels alder cyclisation

The Diels Alder reaction is known as a pericyclic reaction and consist of a dienophile and a diene. The π orbitals of the dienophile form σ bonds with the π orbitals of the diene. The resulting product will have a lower energy due to increased orbital overlap. Depending on the number of electrons involved, the reaction can be allowed or forbidden according to the Woodward-Hoffmann rules.

Fig12. Diels Alder reaction between ethylene and butadiene

Optimizing cis butadiene and ethylene

Cis-butadiene and ethylene were optimized to a minimum using the AM1 and HF/3-21G level of theory and the results are shown in the table below.

Conformer	Structure	Level of theory	Point Group	Energy/ Hartrees	Log file
cis butadiene		AM1	C2v	0.04879719	log file
cis butadiene		HF/3-21G	C2v	-154.05394316	log file
Ethylene		AM1	C2h	0.02619027	log file
Ethylene		HF/3-21G	C2h	-77.60098811	log file

HOMO and LUMO of cis butadiene and ethylene

The HOMO and LUMO were visualized using Gaussview and noted whether the orbitals were symmetric or anti-symmetric.

Conformer	Orbital	Diagram	Symmetry
cis butadiene	LUMO		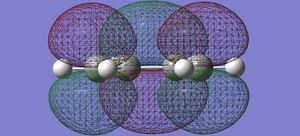symmetric
cis butadiene	HOMO		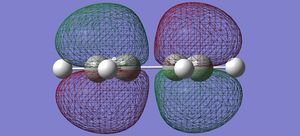anti-symmetric
Ethylene	LUMO		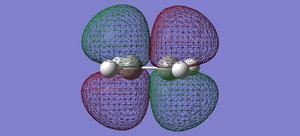anti-symmetric
Ethylene	HOMO		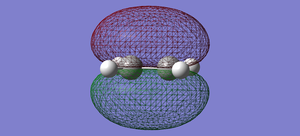symmetric

This table indicated HOMO-LUMO interactions between the diene and dienophile in the Diels Alder cycloaddition because the orbitals that interact need to be of the same symmetry. When the two reactants come together in the cycloaddition the dienophile attacks from below and new bonds are formed on the same face. Using Woodward-Hoffmann analysis, the reaction can be determined to be thermally allowed or not using the following expression - (4q + 2)_s + (4r)_a. In this case this expression has a value of one, meaning that the reaction is thermally allowed. The orbitals that interact have to match and that is why the LUMO of one reactant interacts with the HOMO of the other as when they form bonds their symmetry must match.

Transition structures

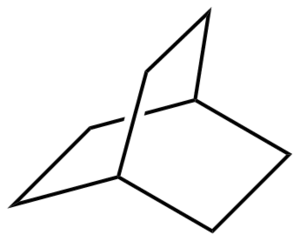
The transition state was drawn in Gaussview by drawing Bicyclo[2.2.2]octane, as shown in figure 13. Removing two carbon atoms and removing/adding bonds as appropriate gave a rough guess of the transition structure. The two reactants were then placed 2.2 Å apart and optimized using TS(Berny) and both the AM1 and HF/3-21G levels of theory were used.

Fig13. bicyclo 2.2.2 octane

Structure	Level of theory	Energy/ Hartrees	Imaginary frequency/ cm-1	Log file
	AM1	0.11165466	-956.22	log file
	HF/3-21G	-231.60320855	-818.44	log file

The table shows the energies and imaginary frequencies of the transition state at two different levels of theory. These frequencies correspond to the bonds forming and breaking in the Diels Alder cycloaddition reaction.

IRC analysis was carried out to confirm that the transition states were found and to confirm the local energy minimum.

Level of theory	Total Energy along IRC	RMS Gradient Norm along IRC	Log file
HF/3-21G		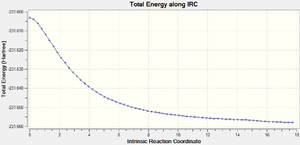	log file

As the table below suggests the imaginary vibration is synchronous and is involved in the bond formation in the Diels Alder cycloaddition reaction whereas the lowest positive frequency is not involved in bond formation in the transition structure and is not synchronous.

Structure	Frequency/ cm-1	Description
	-818.44	synchronus
	116.54	asynchronus

The HOMO and LUMO of the transition structures can be seen below. It is seen that the HOMO of the resulting adduct with two new sigma bonds is anti-symmetric.

Conformer	Orbital	Diagram	Symmetry
Transition state diels alder	LUMO		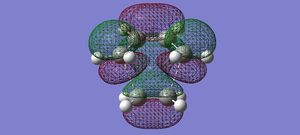symmetric
Transition state diels alder	HOMO		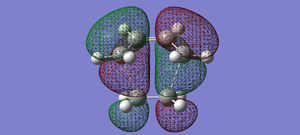anti-symmetric

Comparing bond lengths in the Transition Structure

The AM1 and HF/3-21G levels of theory were compared by looking at the bond length:

	C4-C11/ Å	C11-C7/ Å	C7-C9/ Å
AM1 Semi Empirical	2.11943	1.38183	1.39749
HF/3-21G	2.20960	1.36995	1.39443

The geometries of both levels of theory are similar; the higher level of theory is shown to give lower bond lengths. The literature values of carbon carbon double bonds are 1.334 Å and a single bond is 1.544 Å. The carbon Van Der Waals Radius is reported to be 1.70 Å.

Looking at the HF/3-21G level of theory, it can be seen that the bonds in the cis butadiene have lengths in-between those of single and double bonds. The partial σ bond between the two fragments is 2.20960 Å, which is lower than two Van Der Waals radii, indicating that there is an interaction in the transition state.

Fig14. Labelled Transition Structure

Cyclohexa-1,3-diene and maleic anhydride cycloaddition

The dienophile may have substituents that have π orbitals that can interact with the double bond that is formed in the product. This can lead to regiochemistry, in other words the endo or exo product. Activation energies can be worked out computationally to show which product is preferred and orbitals can be observed to offer explanation to the calculated activation energies.

Working out the reactants

Cyclohexa-1,3-diene and maleic anhydride were drawn, cleaned and optimized with to a HF/3-21G level of theory. The log file for Cyclohexa-1,3-diene can be found here and maleic anhydride here. The HOMO and LUMO were then visualized using Gaussview and noted whether the orbitals were symmetric or anti-symmetric.

Conformer	Orbital	Diagram	Symmetry
cyclohexa-1,3-diene	LUMO		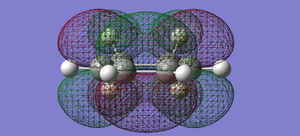symmetric
cyclohexa-1,3-diene	HOMO		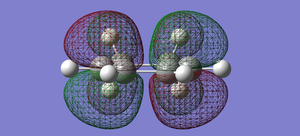anti-symmetric
maleic anhydride	LUMO		anti-symmetric
maleic anhydride	HOMO		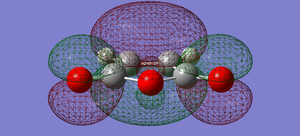symmetric

Transition structures energies and frequencies

The transition structure was found using the QST2 method. The optimized reactant molecules were optimized to a minimum using the HF/3-21G level of theory to give the expected product. This was put in the product window. In the reactant window the two reactant molecules were set 1.5 Å apart.

Type of approach	Structure	Level of theory	Energy/ Hartrees	Imaginary frequency/ cm-1	Log file
endo		AM1	-0.05150478	-806.55	log file
exo		AM1	-0.05041984	-812.24	log file
endo		HF/3-21G	-605.61036818	-643.59	log file
exo		HF/3-21G	-605.60359120	-647.42	log file

Comparing bonds in Transition structures

Fig15. Endo labelled

Fig16. Exo labelled

The bond lengths for the sigma forming bonds between the diene and dienophile in the endo product are 2.23161 Å (C11-C2) compared to 2.26010 Å (C13-C2) of the exo transition state. The longer distance for the exo transition state indicate that the transition state experiences more steric hindrance. This could be because the sp³ hydrogen atoms sterically clash with the -(C=O)-O-(C=O)- component of the maleic anhydride. This does not happen with the endo transition state as the maleic anhydride attacks on the other side of the diene. All of the other bond lengths seem to be fairly similar in length, indicating the major difference is the new bond forming in the transition state which seems harder to form in the exo product as there is more steric strain.

HOMO & LUMO of Transition States

The HOMO and LUMO of the product was visualized using Gaussview. The HOMO and LUMO from the endo and exo do not show strong orbital interaction between the diene and dienophile.

Transition State Type	Orbital	Diagram
Endo	LUMO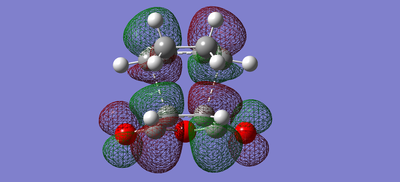
Endo	HOMO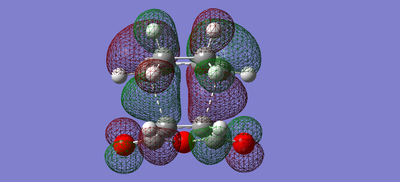
Exo	LUMO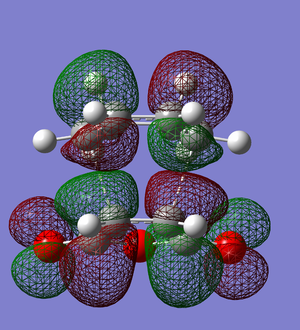
Exo	HOMO

The secondary orbital overlap, as shown in the HOMO-1 orbitals of the endo and exo interaction, show that the endo product has orbital overlap between the -(C=O)-O-(C=O)- of the maleic anhydride and the double bond formed in the product. This shows that the endo product is more stable and should form more easily, therefore the activation energy of the endo product should be lower.

Transition State Type	Orbital	Diagram
Endo	HOMO -1
Exo	HOMO -1

IRC of Transition State

IRC analysis was performed to find the local minimum from the transition states. The local minimum states were confirmed as the RMS gradient reached zero in all cases and the energies of the local minimum were found on the Total Energy graphs.

Transition Type	Level of theory	Total Energy along IRC	RMS Gradient Norm along IRC	Log file
endo	AM1		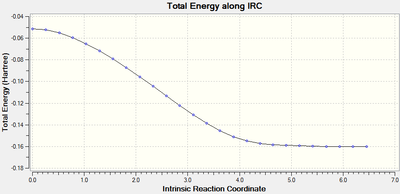	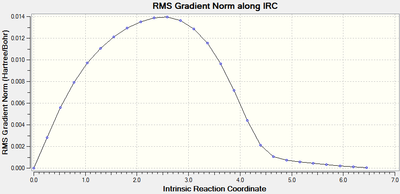log file
exo	AM1		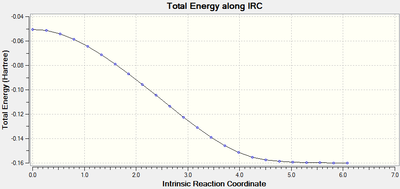	log file
endo	HF/3-21G			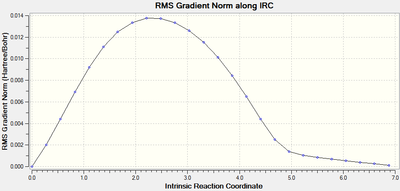log file
exo	HF/3-21G		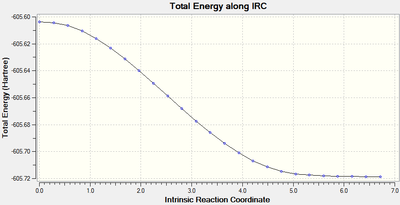	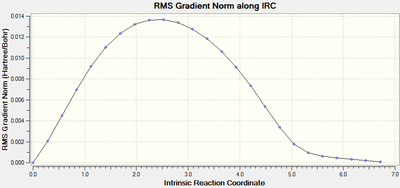log file

Fig17. Endo product

Fig18. Exo product

When running the IRC analysis, the minimum local structure gave the products of the reaction. As shown in figure 17 and 18, the maleic anhydride in the endo product forms on the bottom face whereas the maleic anhydride in the exo product forms on the top face. This is because, in the endo product, the maleic anhydride -(C=O)-O-(C=O)- fragment interacts with the double bond formed in the product.

Activation Energies

The activation energies of the transition states were calculated for the endo and exo product using two levels of theory,AM1 and 3-21G, to figure out which product is preferred.

Summary of energies (in hartree)

	AM1			HF/3-21G
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Endo	-0.05150478	0.133494	0.143683	-605.61036818	-605.414904	-605.405478
Exo	-0.05041984	0.134881	0.144881	-605.6035912	-605.408138	-605.398679
Cyclohexa-1,3-diene	0.02795812	0.152537	0.157031	-230.53967094	-230.407712	-230.403444
Maleic Anhydride	-0.12182416	-0.063345	-0.058191	-375.10351315	-375.042898	-230.403444

*1 hartree = 627.509 kcal/mol

Summary of activation energies (in kcal/mol)

	AM1	AM1	HF/3-21G	HF/3-21G
	at 0 K	at 298.15 K	at 0 K	at 298.15 K
ΔE (endo)	27.80	28.14	22.41	22.61
ΔE (Exo)	28.67	28.89	26.65	26.88

Two conclusions can be drawn from the table. The first is that using 3-21G level of theory predicts that the transition state energies are lower. This could be because 3-21G predicts the transition state to be more stable and more accurate to the experimental transition state. Lastly, it can be seen that the endo product has a lower activation energy. This agrees with the hypothesis set in the secondary orbital section which concluded that due to secondary orbital overlap of the endo product the activation energy would be lower.

Conclusion

Gaussview was used to computationally model cycloaddition reactions. Gaussview allowed the computational models of the transition structures to be calculated and for the frequencies to be observed. Different levels of theory were used in the calculation: AM1, HF/3-21G and B3LYP/6-31G*. It also allowed the activation energies to be worked out and for the orbitals to be visualized. The experiment involved the study of the Cope Rearrangement and the Diels Alder reaction.

The Cope Rearrangement can occur through either a chair or a boat transition state. Both of these possibilities were worked out using three different methods and it was found that the lowest activation energy occurred with a chair formation.

The Diels Alder reaction was studied by applying methods used in the Cope Rearrangement. A simple Diels Alder reaction was studied first followed by a more complicated reaction that gave two different products - the exo and endo product. HOMO and LUMO interactions were studied to see how the diene and dienophile interacted and it was found that the HOMO of the diene interacted with the LUMO of the dienophile and the LUMO of the diene interacted with the HOMO of the dienophile. The transition states were optimized and it was found that the endo product was energetically favourable. Overall it seems that computational methods are a good method in investigating chemical reactions. However there are still factors that Gaussview may neglect when running calculations, such as the solvent effect on the reactants.

References

<references>