Rep:Mod:JLS86216386

Introduction

This page is a computational chemistry exercise based on the instructions provided by Dr. Patricia Hunt for the Imperial College Year 3 Laboratory course. Gaussview 5.0 was used to carry out optimisation of the molecule, as well as frequency, molecular orbital (MO) and natural bond orbital (NBO) analysis. Alternatively, jobs for large molecule were submitted to Imperial College High Performance Computing (HPC) portal.

In the calculation, SCF (Self-consistent field) represents schrödinger solution for electron density and energy while OPT represents nuclear position. Different nuclear positions were tried out until the lowest energy position represented by its corresponding energy and electron density was achieved.

B3LYP is the common method used in this exercise, which means the type of approximations which are made in solving the schrödinger equation.
6-31G(d,p) is the common basis set used, unless otherwise specified. This was chosen for a balance between calculation accuracy and speed in determining the optimum nuclear positions. Basis sets determine the number of functions used to describe the electronic structure.

Week 1- Optimisation

BH₃ Optimisation

Symmetry of the BH₃ molecule was firstly broken by setting each B-H bond to 1.53 Å, 1.54 Å and 1.55 Å respectively.

Using basis set 3-21G

Table 1. BH3 optimised with 3-21G Link to log file File type .log Calculation Type FOPT Calculation Method RB3LYP Basis Set 3-21G Final Energy/ a.u. -26.46226429 Gradient 0.00008851 Dipole Moment/ Debye 0.00 Point Group CS Calculation time/ sec 19.0

Item Value Threshold Converged? Maximum Force 0.000220 0.000450 YES RMS Force 0.000106 0.000300 YES Maximum Displacement 0.000940 0.001800 YES RMS Displacement 0.000447 0.001200 YES Predicted change in Energy=-1.672478D-07 Optimization completed. -- Stationary point found. ----------------------------  ! Optimized Parameters  !  ! (Angstroms and Degrees)  ! -------------------------- --------------------------  ! Name Definition Value Derivative Info.  ! --------------------------------------------------------------------------------  ! R1 R(1,2) 1.1948 -DE/DX = -0.0002  !  ! R2 R(1,3) 1.1947 -DE/DX = -0.0002  !  ! R3 R(1,4) 1.1944 -DE/DX = -0.0001  !  ! A1 A(2,1,3) 120.0157 -DE/DX = 0.0  !  ! A2 A(2,1,4) 119.986 -DE/DX = 0.0  !  ! A3 A(3,1,4) 119.9983 -DE/DX = 0.0  !  ! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0  ! -------------------------------------------------------------------------------- GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad Forces and displacements are successfully converged i.e. there is no further change in energy for a small displacement along the potential energy surface. The optimised B-H bond length is 1.19 Å and H-B-H bond angle is 120.0°. The expected D3h point group was not obtained by the calculation above as the program requires very accurate numbers to achieve the correct point group. However, the molecule shows D3h symmetry for up to 3 d.p. in bond length and 1 d.p. in bond angle respectively.

Graphs of how energy and gradient changes over the process of optimisation are presented below.

Figure 1. Graph of Energy against optimisation steps

Figure 2. Graph of RMS Gradient against optimisation steps

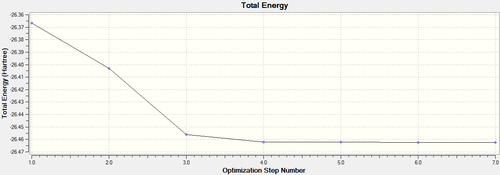
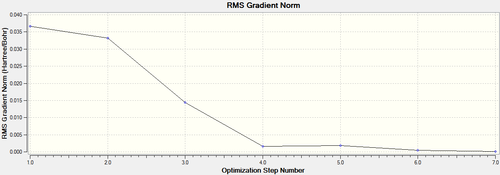
Figure 1. represents the energy of the Potential Energy Surface while Figure 2. represents the first derivative/gradient of Figure 1. At the energy minimum point (last structure in the optimisation process), energy is the lowest (most negative) as shown in Figure 1. and there is minimal net force to shift the nuclear position away from equilibrium, as represented by RMS gradient reaching to a minimum in Figure 2. Hence the nuclei are at their stable equilibrium position.

Using basis set 6-31G(d,p)

Table 2. BH3 optimised with 6-31G(d,p) Link to log file File type .log Calculation Type FOPT Calculation Method RB3LYP Basis Set 6-31G(d,p) Final Energy/ a.u. -26.61532358 Gradient 0.00008206 Dipole Moment/ Debye 0.00 Point Group CS Calculation time/ sec 18.0

Item Value Threshold Converged? Maximum Force 0.000204 0.000450 YES RMS Force 0.000099 0.000300 YES Maximum Displacement 0.000875 0.001800 YES RMS Displacement 0.000418 0.001200 YES Predicted change in Energy=-1.452109D-07 Optimization completed. -- Stationary point found. ----------------------------  ! Optimized Parameters  !  ! (Angstroms and Degrees)  ! -------------------------- --------------------------  ! Name Definition Value Derivative Info.  ! --------------------------------------------------------------------------------  ! R1 R(1,2) 1.1928 -DE/DX = -0.0002  !  ! R2 R(1,3) 1.1926 -DE/DX = -0.0002  !  ! R3 R(1,4) 1.1924 -DE/DX = 0.0  !  ! A1 A(2,1,3) 120.0146 -DE/DX = 0.0  !  ! A2 A(2,1,4) 119.9866 -DE/DX = 0.0  !  ! A3 A(3,1,4) 119.9988 -DE/DX = 0.0  !  ! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0  ! -------------------------------------------------------------------------------- GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad Forces and displacements are successfully converged. The optimised B-H bond length is 1.19Å (lit. 1.19 Å) and H-B-H bond angle is 120.0°. The calculated bond length agrees closely with the literature value. The point group was still calculated to be CS instead of the expected D3h. This is due to that the convergence criteria were not tight enough and the program requires a very accurate number to achieve the correct symmetry. The bond length and bond angle values, however, confirm that D3h is the actual point group.

GaBr₃ optimisation using basis set LanL2DZ

Pseudo-potentials were used for heavy atoms Ga and Br for a faster calculation.

Table 3. GaBr3 optimised with LanL2DZ DOI:10042/27601 File type .log Calculation Type FOPT Calculation Method RB3LYP Basis Set LANL2DZ Final Energy/ a.u. -41.69989295 Gradient 0.00402846 Dipole Moment/ Debye 0.00 Point Group D3h Calculation time/ sec 27.8

Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000003 0.001800 YES RMS Displacement 0.000002 0.001200 YES Predicted change in Energy=-1.282687D-12 Optimization completed. -- Stationary point found. ----------------------------  ! Optimized Parameters  !  ! (Angstroms and Degrees)  ! -------------------------- --------------------------  ! Name Definition Value Derivative Info.  ! --------------------------------------------------------------------------------  ! R1 R(1,2) 2.3502 -DE/DX = 0.0  !  ! R2 R(1,3) 2.3502 -DE/DX = 0.0  !  ! R3 R(1,4) 2.3502 -DE/DX = 0.0  !  ! A1 A(2,1,3) 120.0 -DE/DX = 0.0  !  ! A2 A(2,1,4) 120.0 -DE/DX = 0.0  !  ! A3 A(3,1,4) 120.0 -DE/DX = 0.0  !  ! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0  ! -------------------------------------------------------------------------------- GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad Forces and displacements are successfully converged. The optimised Ga-Br bond length is 2.35 Å (lit. 2.3525 Å) and Br-Ga-Br bond angle is 120.0°. The calculated bond length is close to the literature value, confirming the effectiveness of calculation using pseudo-potentials.

BBr₃ optimisation using mixed basis sets

Pseudo-potential was used for Br.

Table 4. BBr3 optimised with mixed basis sets: 6-31G(d,p) for B and LanL2DZ for Br DOI:10042/27606 File type .log Calculation Type FOPT Calculation Method RB3LYP Basis Set Gen Final Energy/ a.u. -64.43645388 Gradient 0.00000943 Dipole Moment/ Debye 0.00 Point Group CS Calculation time/ sec 35.3

Item Value Threshold Converged? Maximum Force 0.000016 0.000450 YES RMS Force 0.000010 0.000300 YES Maximum Displacement 0.000067 0.001800 YES RMS Displacement 0.000040 0.001200 YES Predicted change in Energy=-1.574158D-09 Optimization completed. -- Stationary point found. ----------------------------  ! Optimized Parameters  !  ! (Angstroms and Degrees)  ! -------------------------- --------------------------  ! Name Definition Value Derivative Info.  ! --------------------------------------------------------------------------------  ! R1 R(1,2) 1.9339 -DE/DX = 0.0  !  ! R2 R(1,3) 1.934 -DE/DX = 0.0  !  ! R3 R(1,4) 1.934 -DE/DX = 0.0  !  ! A1 A(2,1,3) 120.0011 -DE/DX = 0.0  !  ! A2 A(2,1,4) 120.0018 -DE/DX = 0.0  !  ! A3 A(3,1,4) 119.9971 -DE/DX = 0.0  !  ! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0  ! -------------------------------------------------------------------------------- GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad Forces and displacements are successfully converged. The optimised B-Br bond length is 1.93 Å (lit. 1.893 Å for D3h point group) and Br-B-Br bond angle is 120.0°. The calculated bond length is close to the literature value. Although Cs was obtained as the point group, the bond length and bond angle values confirm that D3h is the actual point group.

Comparing the bond lengths of BH₃, BBr₃ and GaBr₃

Table 5. Comparison of bond lengths of BH3, BBr3and GaBr3
Bond	B-H	B-Br	Ga-Br
Bond length/ Å	1.19	1.93	2.35

All the three molecules have a trigonal planar structure with D_3h point group and three 2-centre-2-electron bonds between the central atom and the ligands. It was observed from the pair of B-H and B-Br that when the central atom is kept the same, the larger the ligand, the longer the bond distance. The electronic configuration of H is 1s¹ and that of Br is [Ar]3d¹⁰4s²4p⁵. Both H and Br requires one additional electron to achieve their stable electronic configuration. However, the electron used for bonding for H is from 1s orbital whereas the electron used for bonding for Br is from 4p orbital. Radial distribution function shows that electron density for a 4p orbital would be found much further away from the nucleus than that of 1s orbital. The more diffused orbital for Br would then mean a poor orbital overlap with 2p orbital of B, resulting in a weaker and longer bond. Besides the poor orbital overlap for B-Br, there is also a energy mismatch between B and Br. Electronegativity difference between B and Br (0.8) is larger than that between B and H (0.1). In terms of a molecular orbital diagram, this corresponds to a larger gap in the energy level of atomic orbitals for B and Br and a smaller stabilisation energy from the resulting bonding molecular orbital. The electrons are hence higher in energy and less attracted to the nucleus, resulting in a weaker bond and bond length increases.

It was observed from the pair of B-Br and Ga-Br that when the ligand is kept the same, the larger the central atom, the longer the bond distance. Both B and Ga are group 13 elements and they form bond using their np¹ electron where n is the period number. For B, n=2 but for Ga, n=4. Applying similar reasoning as above, electron density for 4p orbital would be further away from the nucleus that that for 2p orbital according to the radial distribution function. In addition, the electronegativity difference for Ga-Br is (1.2) is larger than that of B-Br (0.8), resulting in greater energy mismatch in the molecular orbital diagram. Overall these lead to weaker and longer bond in Ga-Br.

Definition of a Bond in Gaussview

Table 6. Intermediate structures in the Optimisation of BH3
Optimisation step	1	2	3	4	5	6	7
Structure
B1-H2 distance	1.54	1.45	1.27	1.19	1.19	1.19	1.19

By measuring bond distances of all intermediate geometries from the optimisation of BH₃, it was realised that when the internuclear distance between B and H is above 1.19 Å, a bond was not drawn by Gaussview and a bond was drawn for distance equal to 1.19 Å. This shows that there is a threshold value for which Gaussview defines as a bond. The value represents the bond distance for which the energy is around the minimum along a potential energy surface. At this distance, there is a balance between maximising electron nucleus attraction and minimising nucleus-nucleus repulsion. A covalent bond is hence defined as the built up of electron density that holds two nuclei together to a equilibrium position by overlap of their atomic valence orbitals. At long distance, nuclei are far apart and electrons can no longer form a bond and the electron-nucleus attraction decreases and a bond is not drawn by Gaussview. However, the threshold value is determined rather arbitrarily based on organic molecules. Therefore, using bond distance as a criteria for bond is a potential problem when applied to inorganic molecules and especially other types of bond besides covalent bond, e.g. ionic, metallic or hydrogen bonding where there are electrostatic attraction between the oppositely charged ions or partially charged atoms.

Week 1- Frequency and Population Analysis

BH₃ Frequency Analysis

Initial attempt results in three of the low frequencies being greater than ±15cm^-1 which is at an unacceptable level of accuracy.

 Low frequencies ---   -0.0004    0.0003    0.0003   33.8606   41.5989   43.7038
 Low frequencies --- 1163.5023 1213.4686 1213.5878

It was realised that the optimised BH₃ structure used is C_S instead of the correct D_3h. The inaccurate numbers which previously led to the wrong point group assignment are now manifested into deviation for calculated low frequencies. BH₃ was re-optimised by checking 'use tight convergence criteria' and typing additional keyword 'int=ultrafine scf=conver=9' to tighten the convergence criteria for the nuclear and the electronic part respectively. This will be referred as "tight convergence criteria" in the subsequent calculations.

Table 7. BH3 optimised with 6-31G(d,p) and tight convergence criteria Link to log file File type .log Calculation Type FOPT Calculation Method RB3LYP Basis Set 6-31G(d,p) Final Energy/ a.u. -26.61532364 Gradient 0.00000211 Dipole Moment/ Debye 0.00 Point Group D3h Calculation time/ sec 6.0

Item Value Threshold Converged? Maximum Force 0.000004 0.000015 YES RMS Force 0.000003 0.000010 YES Maximum Displacement 0.000017 0.000060 YES RMS Displacement 0.000011 0.000040 YES Predicted change in Energy=-1.021912D-10 Optimization completed. -- Stationary point found. ----------------------------  ! Optimized Parameters  !  ! (Angstroms and Degrees)  ! -------------------------- --------------------------  ! Name Definition Value Derivative Info.  ! --------------------------------------------------------------------------------  ! R1 R(1,2) 1.1923 -DE/DX = 0.0  !  ! R2 R(1,3) 1.1923 -DE/DX = 0.0  !  ! R3 R(1,4) 1.1923 -DE/DX = 0.0  !  ! A1 A(2,1,3) 120.0 -DE/DX = 0.0  !  ! A2 A(2,1,4) 120.0 -DE/DX = 0.0  !  ! A3 A(3,1,4) 120.0 -DE/DX = 0.0  !  ! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0  ! -------------------------------------------------------------------------------- GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad Forces and displacements are successfully converged. The optimised B-H bond length is 1.19Å (lit. 1.19 Å) and H-B-H bond angle is 120.0°. The calculated bond length agrees closely with the literature value. The expected D3h was obtained due to the tight convergence criteria being applied. The total energy is also lower and the gradient is smaller than the optimisation carried out without the tight convergence criteria. Hence the nuclear position is more precisely determined/ close to the true value of position along the potential energy surface with the tight convergence criteria.

Alternatively, BH₃ can be restricted to D_3h point group for optimisation. While this is a good approach for molecules with established point group, this shall not be bluntly applied to molecules with unknown point group. Hence the method of using tighter criteria is more recommended. Results for the frequency calculation is presented below.

Table 8. BH3 Frequency Analysis Link to log file File type .log Calculation Type FREQ Calculation Method RB3LYP Basis Set 6-31G(d,p) Final Energy/ a.u. -26.61532364 Gradient 0.00000215 Dipole Moment/ Debye 0.00 Point Group D3h Calculation time/ sec 6.0

Low frequencies --- -11.7227 -11.7148 -6.6070 0.0012 0.0278 0.4278 Low frequencies --- 1162.9743 1213.1388 1213.1390 1 2 3 A2" E' E' Frequencies -- 1162.9743 1213.1388 1213.1390 Red. masses -- 1.2531 1.1072 1.1072 Frc consts -- 0.9986 0.9600 0.9600 IR Inten -- 92.5682 14.0550 14.0544 Atom AN X Y Z X Y Z X Y Z 1 5 0.00 0.00 0.16 -0.10 0.00 0.00 0.00 0.10 0.00 2 1 0.00 0.00 -0.57 0.81 0.00 0.00 0.00 0.08 0.00 3 1 0.00 0.00 -0.57 0.14 0.39 0.00 -0.39 -0.59 0.00 4 1 0.00 0.00 -0.57 0.14 -0.39 0.00 0.39 -0.59 0.00 4 5 6 A1' E' E' Frequencies -- 2582.5822 2715.7189 2715.7199 Red. masses -- 1.0078 1.1273 1.1273 Frc consts -- 3.9604 4.8987 4.8987 IR Inten -- 0.0000 126.3320 126.3260 Atom AN X Y Z X Y Z X Y Z 1 5 0.00 0.00 0.00 0.11 0.00 0.00 0.00 0.11 0.00 2 1 0.00 0.58 0.00 0.02 0.00 0.00 0.00 -0.81 0.00 3 1 0.50 -0.29 0.00 -0.60 0.36 0.00 0.36 -0.19 0.00 4 1 -0.50 -0.29 0.00 -0.60 -0.36 0.00 -0.36 -0.19 0.00

The low frequencies are within ±15cm^-1 and the 'real' frequency is within 1 cm^-1 to 1163 cm^-1 provided by Hunt. All 'real' frequencies are positive. Hence the values obtained are correct.

Table 9. BH3 Vibrations
No.	1	2	3	4	5	6
Vibration
Type of motion	Umbrella motion	Scissoring and rocking motion	Scissoring motion	Symmetric stretch	Asymmetric stretch	Asymmetric and symmetric stretch
Description	All the H atoms move up and down across a mirror plane in a concerted motion.	The BH2 fragment at the bottom of the picture undergoes a scissoring motion with the H atom at the top. The BH2 fragment undergoes rocking motion within itself.	Two H atoms bend towards and away from each other in a concerted motion while the third hydrogen remains stationary.	All the three H atoms move in and out in a concerted motion while the B atom is stationary.	Two H atoms move in and out in an alternating motion.	The two H atoms at the bottom of the picture and the hydrogen at the top move in and out in an alternating motion. The two H atoms at the bottom move in and out together.
Frequency/cm-1	1163	1213	1213	2583	2716	2716
Intensity	93	14	14	0	156	156
Symmetry D3h Point Group	A2"	E'	E'	A1'	E'	E'

Figure 3. IR of BH₃ with vibration no. labelled

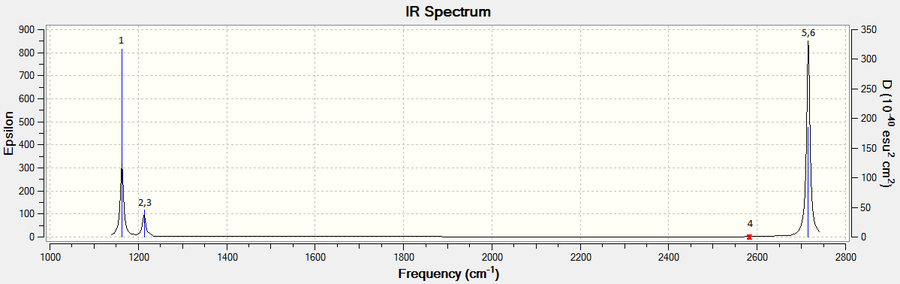
Although there are six vibrations, only three peaks are observed in the IR spectrum. This is because two pairs (2,3 and 5,6) of the vibrations are degenerate and occur at the same frequency while vibration 4 has zero intensity as the vibrations cancel out each other in a symmetric stretch and do not cause a change in the dipole moment in the molecule, which is a criterion for any vibrations to be IR active. Conversely, those modes of vibrations which lead to a large change in dipole moment in the molecule would have high intensity in the IR spectrum.

GaBr₃ Frequency Analysis

Table 10. GaBr3 Frequency Analysis DOI:10042/27618 File type .log Calculation Type FREQ Calculation Method RB3LYP Basis Set LANL2DZ Final Energy/ a.u. -41.70082783 Gradient 0.00000011 Dipole Moment/ Debye 0.00 Point Group D3h Calculation time/ sec 13.9

Low frequencies --- -0.5252 -0.5247 -0.0024 -0.0010 0.0235 1.2010 Low frequencies --- 76.3744 76.3753 99.6982 1 2 3 E' E' A2" Frequencies -- 76.3744 76.3753 99.6982 Red. masses -- 77.4211 77.4212 70.9513 Frc consts -- 0.2661 0.2661 0.4155 IR Inten -- 3.3447 3.3447 9.2161 Atom AN X Y Z X Y Z X Y Z 1 31 -0.39 0.00 0.00 0.00 0.39 0.00 0.00 0.00 0.89 2 35 0.63 0.00 0.00 0.00 0.41 0.00 0.00 0.00 -0.26 3 35 -0.15 -0.45 0.00 0.45 -0.37 0.00 0.00 0.00 -0.26 4 35 -0.15 0.45 0.00 -0.45 -0.37 0.00 0.00 0.00 -0.26 4 5 6 A1' E' E' Frequencies -- 197.3371 316.1825 316.1863 Red. masses -- 78.9183 72.2067 72.2066 Frc consts -- 1.8107 4.2531 4.2532 IR Inten -- 0.0000 57.0704 57.0746 Atom AN X Y Z X Y Z X Y Z 1 31 0.00 0.00 0.00 0.82 0.00 0.00 0.00 0.82 0.00 2 35 0.00 0.58 0.00 -0.01 0.00 0.00 0.00 -0.47 0.00 3 35 -0.50 -0.29 0.00 -0.35 -0.20 0.00 -0.20 -0.12 0.00 4 35 0.50 -0.29 0.00 -0.35 0.20 0.00 0.20 -0.12 0.00

The lowest real mode is 76 cm^-1 with symmetry label E'. Low frequencies are within ±15 cm^-1 and all real frequencies are positive, representing an energy minimum.

Table 11. GaBr3 Vibrations
No.	1	2	3	4	5	6
Vibration
Vibration	Scissoring and rocking motion	Scissoring motion	Umbrella motion	Symmetric stretch	Asymmetric stretch	Asymmetric and symmetric stretch
Description	The GaBr2 fragment at the bottom of the picture undergoes a scissoring motion with the Br atom at the top. The GaBr2 fragment undergoes rocking motion within itself.	Two Br bend towards and away from each other in a concerted motion while the Ga-Br fragment at the top of the picture moves up and down.	All the Br atoms move up and down across a mirror plane in a concerted motion.	All the three Br atoms move in and out in a concerted motion while the Ga atom is stationary.	Two Br atoms move in and out in an alternating motion.	The two Br atoms at the bottom of the picture and the Br at the top move in and out in an alternating motion. The two Br at the bottom move in and out together.
Frequency/cm-1	76	76	100	197	316	316
Intensity	3	3	9	0	57	57
Symmetry D3h Point Group	E'	E'	A2"	A1'	E'	E'

Figure 4. IR of GaBr₃ with vibration no. labelled

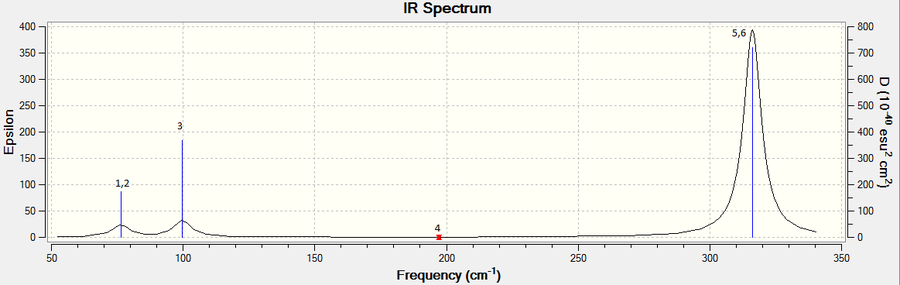
Similar to the case of BH₃, although there are six vibrations, only three peaks are observed in the IR spectrum. Two pairs (1,2 and 5,6) of the vibrations are degenerate and occur at the same frequency while vibration 4 has zero intensity as it is a symmetric stretch and do not cause a change in the dipole moment in the molecule.

Comparing the frequencies of BH₃ and GaBr₃

Table 12. Comparison of frequencies of BH3 and GaBr3
Symmetry D3h Point Group	A2"	E'	E'	A1'	E'	E'
Type of motion	Umbrella motion	Scissoring and rocking motion	Scissoring motion	Symmetric stretch	Asymmetric stretch	Asymmetric and symmetric stretch
BH3
Frequency/cm-1	1163	1213	1213	2583	2716	2716
GaBr3
Frequency/cm-1	100	76	76	197	316	316

The frequencies of GaBr₃ are much lower than that of BH₃. According to Hooke’s law, the frequency of vibration,v is related to the force constant k of a spring and its mass, m, as shown in equation 1. The equation is slightly modified to describe the vibration of diatomic molecules, as shown in equation 2.

where k is the force constant (related to bond strength) of a bond,
the reduced mass of the molecule, where m is the atomic mass and
where c is the speed of light and is the frequency in wavenumber cm^-1.

According to equation 2, the vibrational frequency of a bond is proportional to the square-root of the bond's force constant, and inversely proportional to the square-root of the reduced mass μ of the two atoms. Ga-Br have a higher μ as the atomic mass of Ga and Br is 69.7 and 79.9 respectively while B-H has a lower μ as the atomic mass of B and H is 10.8 and 1.0 respectively. In addition, the Ga-Br bond distance is longer than that of B‑H due to more diffused orbitals of Ga and Br and a poorer orbital overlap. Hence, Ga-Br bond would be weaker and have a smaller force constant than the B‑H bond. Overall, a greater μ and a lower k for Ga-Br result in a lower vibrational frequency of GaBr₃ than BH₃. Note: although the prediction is based on a model for diatomic molecules and a matrix is required to solve for the resultant frequency of the entire molecule, the calculated relative frequency between the two molecules will be same as predicted using this model.

Both molecules have six vibrational frequencies. However, there has been a reordering in the A2" umbrella motion. In BH₃, the A2" mode has the lowest frequency, followed but the doubly degenerate E' modes whereas in GaBr₃, the doubly degenerate E' modes have the lowest frequency, followed by A2". The A2" mode is at a higher frequency and energy in GaBr₃ due to the heavier Br atoms requiring more energy to bend in and out of the plane. In comparison, H is lighter in BH₃ and it requires less energy for them to bend in and out of plane.

The spectra are similar as only three peaks were observed in the IR spectrum when there are actually six modes of vibrations. This is due to two sets of doubly degenerate vibration modes (E') which appear as a single peak each, as well as the A1' mode (symmetric stretch in which there is no net change in dipole moment of the molecule) having zero intensity which is not observed in the IR spectrum.

For both spectra, two modes, A2 and E', lie fairly closely together while the other two modes, A1' and E', also lie fairly close together, but are higher in energy. The three lower energy modes correspond to bending motions of the molecules while the three higher energy modes correspond to stretch motions of the molecules. More energy is required to cause the stretching of the bond due to a change in bond distance and therefore, stretching vibrations are of a higher frequency than bending vibrations.

---

Different methods mean different type of calculation and approximation made in solving the Schrodinger equation while different basis set mean different levels of precision involved in the calculation. Both would lead to different results for calculation upon the same molecule. Hence, using the same method and basis set ensures the consistency and fairness in comparing results between different molecules.
Frequency analysis allows us to match the calculated spectrum with the experimental IR spectrum and be able to associate each peak to a particular vibrational mode, as well as to discover any vibration mode with intensity= 0 in IR spectrum. The positive sign of peaks corresponds to a minimum point along a potential energy surface and hence allows us to ensure that the optimised molecule is at its lowest energy.
The "low frequencies" represent translational or rotational motion from the centre of mass of the molecule. There are six of them as for every non-linear molecule with N atoms, there are 3N-6 vibrational frequencies and the "-6" represent the 6 low frequencies. These should be below ±15 cm^-1 which is much smaller than the 'real' vibrational frequencies.

BH₃ Population Analysis

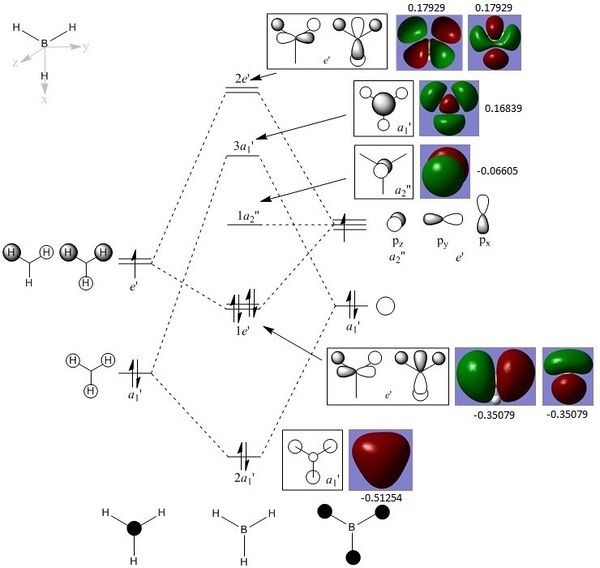
Table 13. BH3 Population analysis DOI:10042/27625 File type .log Calculation Type SP Calculation Method RB3LYP Basis Set 6-31G(d,p) Final Energy/ a.u. -26.61532363 Dipole Moment/ Debye 0.00 Point Group D3h Calculation time/ sec 31.9 It is important to carry out this population analysis on a optimised BH3 with tight convergence criteria. Otherwise, the MO picture generated for the left picture with energy= -0.35079 a.u. would be as unsymmetrical as the one on the right, and the supposedly degenerate pairs would have slightly different energies. MO pictures generated from the population analysis is presented on the right with core-orbital (1S orbital of B) omitted. The calculated MO electron density match well with the LCAO MOs, this confirms the accuracy and usefulness of qualitative MO theory in predicting the real MO. In particular, through-space interaction is clearly illustrated in the calculated MO pictures as jointly shaded area. e.g. for MO with energy= =0.51254 a.u..

Figure 5. MO of BH3

Week 1- Combined

NH₃

Optimisation

Optimisation was carried out with tight convergence criteria as firstly, it ensures the consistency required to compare energies later and secondly, optimisation without tight convergence criteria or even with symmetry set to C_3v still did not give frequency ±15 cm^-1.

Table 14. NH3 optimised with 6-31G(d,p) and tight convergence criteria Link to log file File type .log Calculation Type FOPT Calculation Method RB3LYP Basis Set 6-31G(d,p) Final Energy/ a.u. -56.55776873 Gradient 0.00000323 Dipole Moment/ Debye 1.85 Point Group C3v Calculation time/ sec 14.0

Item Value Threshold Converged? Maximum Force 0.000006 0.000015 YES RMS Force 0.000004 0.000010 YES Maximum Displacement 0.000012 0.000060 YES RMS Displacement 0.000008 0.000040 YES Predicted change in Energy=-9.845972D-11 Optimization completed. -- Stationary point found. ----------------------------  ! Optimized Parameters  !  ! (Angstroms and Degrees)  ! -------------------------- --------------------------  ! Name Definition Value Derivative Info.  ! --------------------------------------------------------------------------------  ! R1 R(1,2) 1.018 -DE/DX = 0.0  !  ! R2 R(1,3) 1.018 -DE/DX = 0.0  !  ! R3 R(1,4) 1.018 -DE/DX = 0.0  !  ! A1 A(2,1,3) 105.7446 -DE/DX = 0.0  !  ! A2 A(2,1,4) 105.7446 -DE/DX = 0.0  !  ! A3 A(3,1,4) 105.7446 -DE/DX = 0.0  !  ! D1 D(2,1,4,3) -111.8637 -DE/DX = 0.0  ! -------------------------------------------------------------------------------- GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad Forces and displacements are successfully converged. The optimised B-Br bond length is 1.02 Å and Br-B-Br bond angle is 105.7°. The expected point group C3v was obtained due to the tight convergence criteria being applied.

Frequency Analysis

Failed frequency analysis without tight convergence criteria nor symmetry set in optimisation. Low frequency is above ±15cm^-1.

 Low frequencies ---  -11.6527  -11.6490   -0.0045    0.0332    0.1311   25.5724
 Low frequencies --- 1089.6616 1694.1736 1694.1736

Failed frequency analysis without tight convergence criteria but with point group restricted to C_3v in optimisation. Low frequency is still above ±15cm^-1.

 Low frequencies ---  -11.6223  -11.5869   -0.0034    0.0243    0.1403   25.5604
 Low frequencies --- 1089.6629 1694.1734 1694.1737

Successful frequency analysis with tight convergence criteria (no restriction of point group is necessary) applied in optimisation.

Table 15. NH3 Frequency Analysis Link to log file File type .log Calculation Type FREQ Calculation Method RB3LYP Basis Set 6-31G(d,p) Final Energy/ a.u. -56.55776872 Gradient 0.00000322 Dipole Moment/ Debye 1.85 Point Group C3 Calculation time/ sec 8.0

Low frequencies --- -0.0138 -0.0030 0.0013 7.0781 8.0927 8.0932 Low frequencies --- 1089.3840 1693.9368 1693.9368 1 2 3 A E E Frequencies -- 1089.3840 1693.9368 1693.9368 Red. masses -- 1.1800 1.0644 1.0644 Frc consts -- 0.8251 1.7996 1.7996 IR Inten -- 145.4273 13.5570 13.5571 Atom AN X Y Z X Y Z X Y Z 1 7 0.00 0.00 0.12 -0.07 0.00 0.00 0.00 0.07 0.00 2 1 0.00 -0.21 -0.53 0.76 0.00 0.00 0.00 0.15 0.26 3 1 0.18 0.11 -0.53 0.08 -0.39 0.22 0.39 -0.53 -0.13 4 1 -0.18 0.11 -0.53 0.08 0.39 -0.22 -0.39 -0.53 -0.13 4 5 6 A E E Frequencies -- 3461.3048 3589.8557 3589.8557 Red. masses -- 1.0272 1.0883 1.0883 Frc consts -- 7.2510 8.2636 8.2636 IR Inten -- 1.0595 0.2699 0.2699 Atom AN X Y Z X Y Z X Y Z 1 7 0.00 0.00 0.04 0.08 0.00 0.00 0.00 0.08 0.00 2 1 0.00 0.55 -0.18 0.02 0.00 0.00 0.00 -0.75 0.31 3 1 -0.47 -0.27 -0.18 -0.56 -0.34 -0.27 -0.34 -0.17 -0.15 4 1 0.47 -0.27 -0.18 -0.56 0.34 0.27 0.34 -0.17 -0.15 Low frequencies are within ±15 cm-1 and all real frequencies are positive numbers, representing an energy minimum.

Population Analysis

Table 16. NH3 Population Analysis Link to log file File type .log Calculation Type SP Calculation Method RB3LYP Basis Set 6-31G(d,p) Final Energy/ a.u. -56.55776863 Dipole Moment/ Debye 1.85 Point Group C3v Calculation time/ sec 3.0

Figure 6. Calculated MO energies Symmetry labels, electron occupancy and energy degeneracy match perfectly with the one provided by W. Locke of Imperial College, shown in Figure 7 on the right.

Figure 7. MO diagram by W. Locke with corresponding energy no. labelled

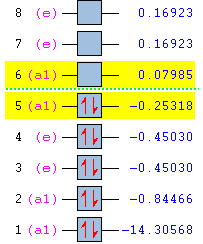
Natural Bond Orbital (NBO)

Figure 8. Charge distribution of NH₃

Figure 9. NBO charges of NH3

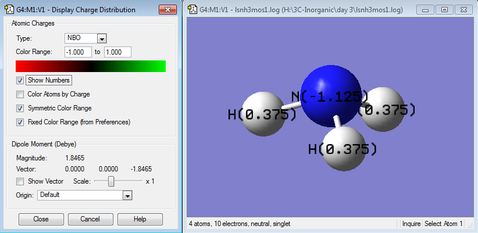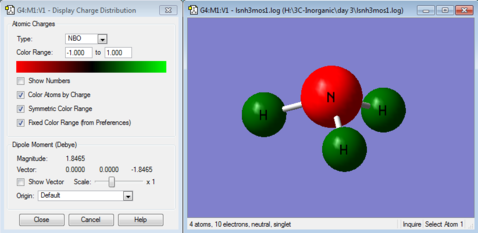
NBO reveals information about atomic like orbitals instead of molecular orbitals in the population analysis. From Figure 9, NBO charge of N is -1.125 (negative represented in red in Figure 8.) while the NBO charge of H is +0.375 (positive represented in green in Figure 8.). Total charge is 0= -1.125+ 3x 0.375 as the molecule is neutral. The negative charge of N is due to N being more electronegative and withdraws electron density from H which has a positive charge.
There is now a resultant dipole moment of 1.85 debye in the direction of N's lone pair as the point group is C_3v instead of D_3h now, where there is no cancellation of dipole moments along the three N-H bonds.

Association Energies of NH₃BH₃

The optimisation was done using the same basis set 6-31G(d,p) with tight convergence criteria so that the results can be compared for reactants and products later.

Optimisation

Table 17. NH3BH3 Optimised with 6-31G(d,p) and tight convergence criteria Link to log file File type .log Calculation Type FOPT Calculation Method RB3LYP Basis Set 6-31G(d,p) Final Energy/ a.u. -83.22468908 Gradient 0.00000138 Dipole Moment/ Debye 5.56 Point Group C1 Calculation time/ sec 61.0

Item Value Threshold Converged? Maximum Force 0.000002 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000034 0.000060 YES RMS Displacement 0.000010 0.000040 YES Predicted change in Energy=-1.180788D-10 Optimization completed. -- Stationary point found. Forces and displacements are successfully converged. The optimised B-H bond length is 1.21 Å, N-H bond length is 1.02 Å and B-N bond length is 1.67 Å.

Frequency Analysis

Table 18. NH3BH3 Frequency Analysis Link to log file File type .log Calculation Type FREQ Calculation Method RB3LYP Basis Set 6-31G(d,p) Final Energy/ a.u. -83.22468906 Gradient 0.00000142 Dipole Moment/ Debye 5.56 Point Group C1 Calculation time/ sec 34.0

Low frequencies --- -7.0696 -0.0010 0.0002 0.0005 2.4900 2.9164 Low frequencies --- 263.3512 632.9541 638.4581 Low frequencies are within ±15 cm-1 and all real frequencies are positive, representing an energy minimum.

Energy Analysis

All energies presented in Table 19. are from optimisation using 6-31G(d,p) basis set with tight convergence criteria for a valid comparison.

Table 19. Comparison of energies of NH3, BH3and NH3BH3
Molecule	NH3	BH3	NH3BH3
Energy/ a.u.	-56.55776873	-26.61532364	-83.22468906

For the association reaction, NH₃ (g)+ BH₃ (g)--> NH₃BH₃ (s)
Energy difference, ΔE=E(product: NH₃BH₃)- E(reactants:(NH₃)+ (BH₃)]= -0.05159669 a.u.
Using the conversion factor, 1H = 2625.5 kJ/mol, ΔE= -0.05159669 x 2625.5= -140 kJ/ mol (2 s.f.).

Therefore, the association energy of combining NH₃ and BH₃ to NH₃BH₃ is -140 kJ/ mol. The negative sign implies that it is energetically favourable to form NH₃BH₃ which is lower in energy than the sum of energies of the reactants, NH₃ and BH₃. Conversely, +140 kJ/ mol would then be the dissociation energy of NH₃BH₃ into NH₃ and BH₃, which is unfavourable.
Thermal energy at room temperature is 2.5 kJ/mol and the bond energy is about 50 times greater than thermal energy, hence the bond energy obtained is a sensible number as it makes sense that the bond formed should be stable at room temperature.
The bond energy of N-B (140 kJ/ mol) is one of the weaker ones among typical diatomic bond strength e.g. isoelectronic C-C bond (347 kJ/ mol). While it is recognised that N-B is formally a dative bond, Gaussian calculation only concerns about electron density and whether a bond is covalent or dative is not distinguished. Poorer orbital overlap between B and N due to size and energy difference can be one reason. Another reason could be that N is electronegative and likes to withdraw electron density and therefore to a certain extent it is unfavourable for N to donate its lone pair to the vacant orbital of B.

It is also worth noting entropy in this association reaction is strongly disfavoured as 2 moles of gas become 1 mole of solid. In reality, whether this reaction happens depends on how large the contribution that entropy has on the reaction, which is not taken into account in the calculation which is only based on nuclear and electronic attraction and repulsion.

Week 2- Part 1

A mini project was conducted on ionic liquids.

Optimisation and Frequency Analysis

All procedures are the same as before (6-31G(d,p) and tight convergence criteria) except using charge= 1.

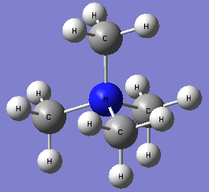
[N(CH₃)₄]⁺

Table 20. [N(CH3)4]+ Optimised with 6-31G(d,p) and tight convergence criteria DOI:10042/27670 File type .log Calculation Type FOPT Calculation Method RB3LYP Basis Set 6-31G(d,p) Charge 1 Final Energy/ a.u. -214.18127215 Gradient 0.00000400 Dipole Moment/ Debye 0.00 Point Group C1 Calculation time 1 hr 22 min 24.3 sec

Item Value Threshold Converged? Maximum Force 0.000007 0.000015 YES RMS Force 0.000002 0.000010 YES Maximum Displacement 0.000047 0.000060 YES RMS Displacement 0.000014 0.000040 YES Predicted change in Energy=-6.552973D-10 Optimization completed. -- Stationary point found. ----------------------------  ! Optimized Parameters  !  ! (Angstroms and Degrees)  ! -------------------------- --------------------------  ! Name Definition Value Derivative Info.  ! --------------------------------------------------------------------------------  ! R1 R(1,2) 1.5094 -DE/DX = 0.0  !  ! R2 R(1,6) 1.5094 -DE/DX = 0.0  !  ! R3 R(1,10) 1.5094 -DE/DX = 0.0  !  ! R4 R(1,14) 1.5094 -DE/DX = 0.0  !  ! R5 R(2,3) 1.0902 -DE/DX = 0.0  !  ! R6 R(2,4) 1.0902 -DE/DX = 0.0  !  ! R7 R(2,5) 1.0902 -DE/DX = 0.0  !  ! R8 R(6,7) 1.0902 -DE/DX = 0.0  !  ! R9 R(6,8) 1.0902 -DE/DX = 0.0  !  ! R10 R(6,9) 1.0902 -DE/DX = 0.0  !  ! R11 R(10,11) 1.0902 -DE/DX = 0.0  !  ! R12 R(10,12) 1.0902 -DE/DX = 0.0  !  ! R13 R(10,13) 1.0902 -DE/DX = 0.0  !  ! R14 R(14,15) 1.0902 -DE/DX = 0.0  !  ! R15 R(14,16) 1.0902 -DE/DX = 0.0  !  ! R16 R(14,17) 1.0902 -DE/DX = 0.0  ! Forces and displacements are successfully converged. The optimised N-C bond length is 1.51 Å and C-H bond length is 1.09 Å. N-C bond is longer than C-H bond as N has a more diffused orbital (2p) than H (1s), resulting in a poorer overlap and a weaker bond. The C-N-C bond angle is 109.5° which corresponds to a tetrahedral structure around the central heteroatom N. This is because that the four methyl substituents are equivalent and there is no lone pair on N due to the positive charge, hence to minimise steric clash to best geometry for [N(CH3)4]+ to adopt is tetrahedral.

Table 21. [N(CH3)4]+ Frequency Analysis DOI:10042/27673 File type .log Calculation Type FREQ Calculation Method RB3LYP Basis Set 6-31G(d,p) Charge 1 Final Energy/ a.u. -214.18127213 Gradient 0.00000392 Dipole Moment/ Debye 0.00 Point Group C1 Calculation time 21 min 39.8 sec

Low frequencies --- -9.7641 -7.9756 -0.0004 -0.0004 0.0005 0.8357 Low frequencies --- 181.5331 287.9414 288.2282 Low frequencies are within ±15 cm-1 and all real frequencies are positive, representing an energy minimum.

[P(CH₃)₄]⁺

Table 22. [P(CH3)4]+ Optimised with 6-31G(d,p) and tight convergence criteria DOI:10042/27671 File type .log Calculation Type FOPT Calculation Method RB3LYP Basis Set 6-31G(d,p) Charge 1 Final Energy/ a.u. -500.82701262 Gradient 0.00000264 Dipole Moment/ Debye 0.00 Point Group C1 Calculation time 36 min 55.9 sec

Item Value Threshold Converged? Maximum Force 0.000008 0.000015 YES RMS Force 0.000003 0.000010 YES Maximum Displacement 0.000044 0.000060 YES RMS Displacement 0.000015 0.000040 YES Predicted change in Energy=-7.863924D-10 Optimization completed. -- Stationary point found. ----------------------------  ! Optimized Parameters  !  ! (Angstroms and Degrees)  ! -------------------------- --------------------------  ! Name Definition Value Derivative Info.  ! --------------------------------------------------------------------------------  ! R1 R(1,2) 1.0933 -DE/DX = 0.0  !  ! R2 R(1,3) 1.0933 -DE/DX = 0.0  !  ! R3 R(1,4) 1.0933 -DE/DX = 0.0  !  ! R4 R(1,17) 1.8164 -DE/DX = 0.0  !  ! R5 R(5,6) 1.0933 -DE/DX = 0.0  !  ! R6 R(5,7) 1.0933 -DE/DX = 0.0  !  ! R7 R(5,8) 1.0933 -DE/DX = 0.0  !  ! R8 R(5,17) 1.8164 -DE/DX = 0.0  !  ! R9 R(9,10) 1.0933 -DE/DX = 0.0  !  ! R10 R(9,11) 1.0933 -DE/DX = 0.0  !  ! R11 R(9,12) 1.0933 -DE/DX = 0.0  !  ! R12 R(9,17) 1.8164 -DE/DX = 0.0  !  ! R13 R(13,14) 1.0933 -DE/DX = 0.0  !  ! R14 R(13,15) 1.0933 -DE/DX = 0.0  !  ! R15 R(13,16) 1.0933 -DE/DX = 0.0  !  ! R16 R(13,17) 1.8164 -DE/DX = 0.0  ! Forces and displacements are successfully converged. The optimised P-C bond length is 1.82 Å and C-H bond length is 1.09 Å. P-C bond is longer than N-C bond in the previous case as although both P and N are in group 15, N bonds through 2p orbital whereas P bonds through 3p orbital which is more diffused. This results in a poorer overlap between P and C and hence a weaker and longer bond. The C-P-C bond angle is 109.9° which corresponds to a tetrahedral structure around the central heteroatom P. This is because that the four methyl substituents are equivalent and there is no lone pair on P due to the positive charge, hence to minimise steric clash to best geometry for P(CH3)4 to adopt is tetrahedral.

Table 23. [P(CH3)4]+ Frequency Analysis DOI:10042/27674 File type .log Calculation Type FREQ Calculation Method RB3LYP Basis Set 6-31G(d,p) Charge 1 Final Energy/ a.u. -500.82701264 Gradient 0.00000273 Dipole Moment/ Debye 0.00 Point Group C1 Calculation time 21 min 19.7 sec

Low frequencies --- -9.9099 -3.8806 0.0019 0.0022 0.0023 16.1356 Low frequencies --- 156.3097 191.8227 192.1255 Although one low frequency is slightly above ±15 cm-1 as the basis set is not good enough, it is still an acceptable range. All real frequencies are positive, representing an energy minimum.

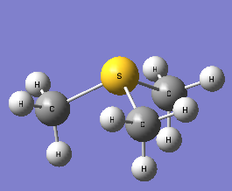
[S(CH₃)₃]⁺

Table 24. [S(CH3)3]+ Optimised with 6-31G(d,p) and tight convergence criteria DOI:10042/27672 File type .log Calculation Type FOPT Calculation Method RB3LYP Basis Set 6-31G(d,p) Charge 1 Final Energy/ a.u. -517.68327545 Gradient 0.00000521 Dipole Moment/ Debye 0.97 Point Group C1 Calculation time 12 min 51.8 sec

Item Value Threshold Converged? Maximum Force 0.000013 0.000015 YES RMS Force 0.000004 0.000010 YES Maximum Displacement 0.000021 0.000060 YES RMS Displacement 0.000007 0.000040 YES Predicted change in Energy=-2.834088D-10 Optimization completed. -- Stationary point found. ----------------------------  ! Optimized Parameters  !  ! (Angstroms and Degrees)  ! -------------------------- --------------------------  ! Name Definition Value Derivative Info.  ! --------------------------------------------------------------------------------  ! R1 R(1,2) 1.8226 -DE/DX = 0.0  !  ! R2 R(1,6) 1.8227 -DE/DX = 0.0  !  ! R3 R(1,10) 1.8226 -DE/DX = 0.0  !  ! R4 R(2,3) 1.0916 -DE/DX = 0.0  !  ! R5 R(2,4) 1.0916 -DE/DX = 0.0  !  ! R6 R(2,5) 1.0914 -DE/DX = 0.0  !  ! R7 R(6,7) 1.0916 -DE/DX = 0.0  !  ! R8 R(6,8) 1.0916 -DE/DX = 0.0  !  ! R9 R(6,9) 1.0914 -DE/DX = 0.0  !  ! R10 R(10,11) 1.0916 -DE/DX = 0.0  !  ! R11 R(10,12) 1.0916 -DE/DX = 0.0  !  ! R12 R(10,13) 1.0914 -DE/DX = 0.0  ! Forces and displacements are successfully converged. The optimised S-C bond length is 1.82 Å and C-H bond length is 1.09 Å. S-C bond length is the same as P-C bond length as both S and P are from period 3 and they bond to C through their 3p orbital. The C-S-C bond angle is 102.7° which corresponds to a trigonal pyramidal structure around the central heteroatom S. There are three methyl groups and one lone pair around the central S. According to valence bond theory, a lone pair is more repulsive than a bond pair. Hence, the lone pair pushes the three bond pairs away from it and the bond angle between the bond pair decreases from 109.5° in a standard tetrahedral molecule such as [N(CH3)4]+ to 102.7° in [S(CH3)3]+ .

Table 25. [S(CH3)3]+ Frequency Analysis DOI:10042/27675 File type .log Calculation Type FREQ Calculation Method RB3LYP Basis Set 6-31G(d,p) Charge 1 Final Energy/ a.u. -517.68327544 Gradient 0.00000525 Dipole Moment/ Debye 0.97 Point Group C1 Calculation time 10 min 7.6 sec

Low frequencies --- -9.3833 -1.6878 -0.0016 0.0011 0.0023 14.5616 Low frequencies --- 162.0743 199.3066 199.8535 Low frequencies are below ±15 cm-1 and all real frequencies are positive, representing an energy minimum.

Combined Population Analysis

Table 26. [N(CH3)4]+ Population Analysis DOI:10042/27676 File type .log Calculation Type SP Calculation Method RB3LYP Basis Set 6-31G(d,p) Charge 1 Final Energy/ a.u. -214.18128131 Dipole Moment/ Debye 0.00 Point Group C1 Calculation time 1 min 12.8 sec

Table 27. [P(CH3)4]+ Population Analysis DOI:10042/27677 File type .log Calculation Type SP Calculation Method RB3LYP Basis Set 6-31G(d,p) Charge 1 Final Energy/ a.u. -500.82697426 Dipole Moment/ Debye 0.00 Point Group C1 Calculation time 1 min 14.2 sec

Table 28. [S(CH3)3]+ Population Analysis DOI:10042/27678 File type .log Calculation Type SP Calculation Method RB3LYP Basis Set 6-31G(d,p) Charge 1 Final Energy/ a.u. -517.68328757 Dipole Moment/ Debye 0.97 Point Group C1 Calculation time 54.1 sec

MO

Table 29. MO Description of N(CH3)4]+ MO No. MO Picture Description 18 There are two nodal planes, each running across the p orbitals of 2 C. Electron density is not very delocalised as it is only on half of C and one H. All the weak through-space anti-bonding between H are overcome by the strong bonding between adjacent atoms C-H. It is overall weakly bonding. 14 There are two nodal planes across the p orbitals of C. There is a node on each of the four C but as it is on the atom, the node is not strong. Electron density is more delocalised than MO 18 as now it is on two half C and two H. All the weak through-space anti-bonding are overcome by the strong bonding within methyl group and weak bonding between methyl groups. It is overall weakly bonding. 10 There are weak through-space antibonding but through space weak bonding between methyl groups and strong bonding between adjacent C-H within each of four methyl groups. There is a nodal sphere around the s orbital of N, which increases the extent of antibonding interaction and more importantly, there are four very strong antibonding nodes which are formed between adjacent atoms N-C. Electron density is delocalised within each methyl but also possible to extend between the methyl groups as isovalue is decreased to 0.01. It is overall strongly bonding. 9 There are weak through-space antibonding but strong bonding between adjacent atoms. There is a nodal plane across the p orbital of N. Each lobe of N's p orbital has in-phase interaction with two methyl groups, in which electron density is delocalised. There is a node on N but as it is on the atom, the node is not strong. It is overall strongly bonding. 6 There are both strong bonding between adjacent atoms and weak bonding through-space. The electron density is delocalised over s orbitals of all atoms (N, C, H). The s orbital of H atoms are contracted in the bonding interaction with C. As all are bonding interactions and no nodes are present, this MO is of the lowest energy for occupied non-core orbital and is overall very strongly bonding.

Figure 10. Chosen MO of N(CH3)4]+ highlighted in yellow

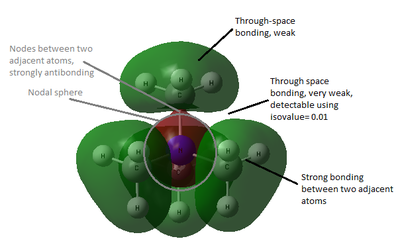
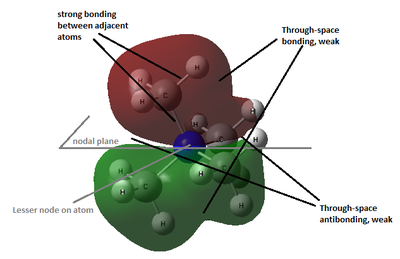
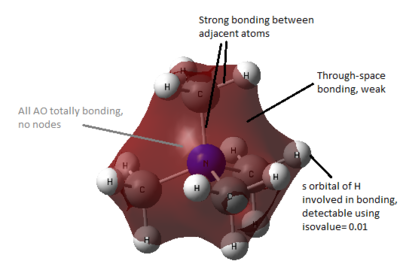
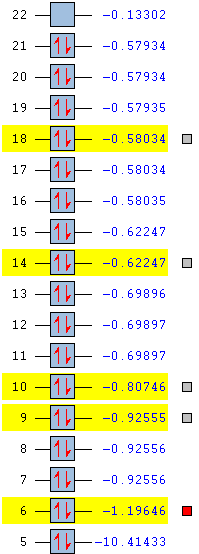
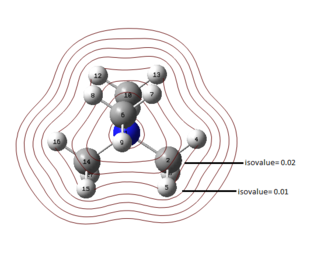
All occupied non-core MO visualised are bonding, although ranging from weakly to strongly bonding as energy decreases from MO 18 to MO 6, as shown in Figure 10. As all visualisations are done at isovalue= 0.02, some weak through-space interactions are only visible when isovalue decreases to 0.01, which essentially expand the edge of electron density by including the more diffused electron density.

Figure 11. Surface contour for MO 6

Figure 12. Surface contour for MO 10

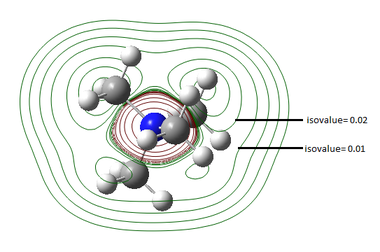By observing the surface contour at isovalue= 0.01, it is observed that for MO 6 (Figure 11), s orbital of H is involved in bonding and for MO 10 (Figure 12), the electron density are delocalised throughout all methyl groups and there is weak through-space bonding between them.

NBO Analysis

Table 30. Comparison of NBO
Molecule	[N(CH3)4]+		[P(CH3)4]+		[S(CH3)3]+
Colour range
Charge distribution by colour
Charge shown in numbers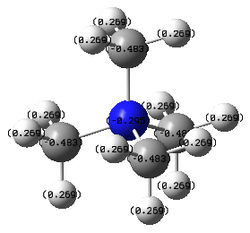
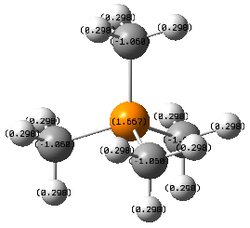
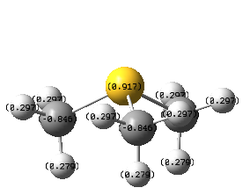
Atom	N	C	P	C	S	C
Tabulated X-C charges	-0.295	-0.483	+1.667	-1.060	+0.917	-0.846
Relative contribution	66%	34%	40%	60%	51%	49%
Electronegativity	3.0	2.5	2.2	2.5	2.5	2.5
Electronegativity Difference relative to C	+0.5		-0.3		0.0

Charge Distribution

In this case, charge distribution in X-C bond (where X=N/P/S) of onium cations is determined by

1. The electronegativity difference between the two atoms (as in the case of NH₃ discussed in week 1) and
2. The extent of positive charge delocalisation. In Scheme 1 shown below, X uses its lone pair to attack a hypothetical "CH₃⁺" to form the onium cation in which the positive charge is generated on X. Depending on the orbital overlap of X with its surrounding atoms, this positive charge is partially delocalised.
   

Scheme 1. Reaction scheme for the formation of onium cations

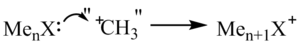
The two reasons above can be used to explain the calculated charge distribution values in the three onium cations.

• In [N(CH₃)₄]⁺, N is more electronegative (+0.5) than C and it is expected that N should have a more negative charge than C. However, N is also positive charged and although much of the positive charge have been delocalised (efficient delocalisation due to good overlap between C and N which are in the same period) to H which is the most electropositive element in the molecule, N is still slightly electron deficient than C as shown by -0.295 (N) and -0.483 (C) charge respectively.
• In [P(CH₃)₄]⁺, P is less electronegative (-0.3) than C so P is more electron deficient and has a more positive charge as expected. The difference of charge distribution (+1.667 and -1.060) is the largest among the three molecules as the positive charge is more localised than the case of N-C. This is due to that P is in period 3 whereas C is in period 2, 3p orbital of P is more diffused and thus does not overlap well with 2p orbital of C, so the positive charge cannot be efficiently delocalised to H via C. This localisation of postive charge, coupled with the lower electronegativity of P, results in a very positive P charge of +1.667.
• In [S(CH₃)₃]⁺, there is nearly zero electronegativity difference between C and S, so S is expected to have the same charge distribution as C. However, the positive charge is more localised on S as the more diffused 3p orbital of S cannot overlap well with 2p orbital of C and thus positive charge cannot be efficiently delocalised, resulting in a more positive charge on S.
  
  

Overall across the three onium cations, as electronegativity decreases for N> S> P, their charge in the X-C bond increases from -0.295< +0.917< +1.667 as they withdraw less electron density.

Figure 13. Charge distribution of S[CH₃]2 with same colour range as Table 30

It is interesting to find out that even for neutral analogue S(CH₃)₂ (Link to log file) where there is no effect of positive charge delocalisation, S is still more positive than C even though they have the same electronegativity. This can then be rationalised by C gaining some electron density from the adjacent H which are more electropositive where as S is only surrounding by C which has the same electronegativity so such electron withdrawing effect is not possible. This results in an alternating charge distribution of δ⁺(H)-δ^-(C)-δ⁺(S)-δ^-(C)-δ⁺(H) which is a favourable polarising effect due to additional electrostatic attraction. This effect can similarly be occuring in [S(CH₃)₃]⁺ and the other onium cations which potentially also led to the more negative charge of C. The charge distribution in S(CH₃)₂ can potentially also be used to prove the fact that the positive charge is more localised on S as the charge increases significantly from +0.209 in S(CH₃)₂ to +0.917 in [S(CH₃)₃]⁺ (difference is greater than the sum of increase of charge in H) when a positive charge is added, assuming the additional methyl group does not have a significant effect on charge distribution.

Relative Contribution

Only one bond is presented as all four bonds are equivalent in each case (confirmed by comparing numbers in data).
[N(CH₃)₄]⁺

     1. (1.98452) BD ( 1) N   1 - C   2 
                ( 66.35%)   0.8146* N   1 s( 25.00%)p 3.00( 74.97%)d 0.00(  0.03%)
                                            0.0000 -0.5000  0.0007  0.0000  0.4755
                                           -0.0001 -0.6460  0.0001  0.3260 -0.0001
                                            0.0126 -0.0064  0.0087  0.0039  0.0051
                ( 33.65%)   0.5801* C   2 s( 20.78%)p 3.81( 79.06%)d 0.01(  0.16%)
                                           -0.0003 -0.4552  0.0237 -0.0026 -0.4879
                                           -0.0207  0.6628  0.0281 -0.3344 -0.0142
                                            0.0288 -0.0145  0.0198  0.0090  0.0117

For the four bonds between nitrogen (atom 1) and carbon (atom 2/6/10/14), 66% of the bond is contributed by the N orbitals which have a hybridisation of 25%s+75%p, while 34% of the bond comes from the C orbital which is 21%s+79%p. Thus N has formed four sp³ hybrid orbitals, each of which interacts with one sp³ hybrid orbital of C. N is more electronegative than C and hence it withdraws more electron density and contributes to a greater extent to the N-C bond.
[P(CH₃)₄]⁺

     4. (1.98030) BD ( 1) C   1 - P  17 
                ( 59.57%)   0.7718* C   1 s( 25.24%)p 2.96( 74.67%)d 0.00(  0.08%)
                                            0.0002  0.5021  0.0171 -0.0020  0.2419
                                           -0.0044 -0.8168  0.0150 -0.1445  0.0027
                                           -0.0133 -0.0024  0.0080 -0.0205 -0.0133
                ( 40.43%)   0.6358* P  17 s( 25.00%)p 2.97( 74.15%)d 0.03(  0.85%)
                                            0.0000  0.0001  0.5000 -0.0008  0.0000
                                            0.0000 -0.2411  0.0003  0.0000  0.8140
                                           -0.0012  0.0000  0.1440 -0.0002 -0.0423
                                           -0.0075  0.0253 -0.0652 -0.0423

For the four bonds between phosphorous (atom 17) and carbon, 40% of the bond is contributed by the P orbitals which have a hybridisation of 25%s+75%p, while 60% of the bond comes from the C orbital which is 25%s+75%p. Thus P has formed four sp³ hybrid orbitals, each of which interacts with one sp³ hybrid orbital of C. P is less electronegative than C and hence its electron density is withdrawn by C and contributes to a smaller extent to the P-C bond.
[S(CH₃)₃]⁺

     1. (1.98631) BD ( 1) S   1 - C   2 
                ( 51.33%)   0.7165* S   1 s( 16.95%)p 4.86( 82.42%)d 0.04(  0.63%)
                                            0.0000  0.0001  0.4117 -0.0075  0.0012
                                            0.0000  0.2283 -0.0100  0.0000  0.7791
                                           -0.0343  0.0000  0.4039  0.0260  0.0267
                                            0.0174  0.0595 -0.0416 -0.0051
                ( 48.67%)   0.6976* C   2 s( 19.71%)p 4.07( 80.16%)d 0.01(  0.14%)
                                            0.0003  0.4437  0.0140 -0.0033 -0.2300
                                            0.0018 -0.7851  0.0061 -0.3635 -0.0098
                                            0.0143  0.0068  0.0231 -0.0223 -0.0096
..........
    21. (1.97342) LP ( 1) S   1           s( 49.14%)p 1.03( 50.85%)d 0.00(  0.01%)
                                            0.0000 -0.0002  0.7010  0.0057 -0.0013
                                            0.0000  0.0000  0.0000  0.0000  0.0000
                                            0.0000  0.0000 -0.7122 -0.0364  0.0000
                                            0.0000  0.0000  0.0000 -0.0101

For the three bonds between sulfur (atom 1) and carbon, 51% of the bond is contributed by the S orbitals which have a hybridisation of 17%s+82%p+1%d, while 49% of the bond comes from the C orbital which is 20%s+80%p. Although the hybridisation data suggests a sp⁵ S and C, such hybridisation is impossible as there are only a maximum of three p orbitals. This can only suggest a high contribution of p orbital/high p character in S-C bond and interestingly, lone pair of S is 49%s+51%p. While theoretically S has formed four sp³ hybrid orbitals, each of which interacts with one sp³ hybrid orbital of C, the high p character of S-C bond and high s character of S's lone pair suggests a degree of inert pair effect down the group as the energy gap between s orbital and p orbital gets larger and it is increasingly harder for electrons in the s orbital to be promoted and involved in hybridisation. As S and C have same electronegativity, charge distribution is roughly equal (51% and 49%)

Overall, relative contribution data can be well explained using electronegativity difference As electronegativity decreases for N> S> P, their relative contribution in the X-C bond decreases from 66%> 51%> 40%.

Formal Charge

[NR₄]⁺ (R=alkyl) is often depicted as the positive charge placed on the nitrogen centre. However, based on the results for [N(CH₃)₄]⁺, this traditional description is not valid.
The "formal" positive charge on the N represents that nitrogen loses one electron by bonding with methyl and hence the N is positively charged. In reality, this positive charge is delocalised in the molecule and in this case, the positive charge is actually located on the hydrogens which are shaded green in the figure of Table 30.

Week 2- Part 2

Optimisation and Frequency Analysis

[N(CH₃)₃(CH₂OH)]⁺

Figure 14. Failed structure of [N(CH3)3(CH2OH)]+

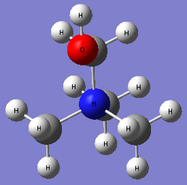
Figure 15. Correct structure of [N(CH3)3(CH2OH)]+

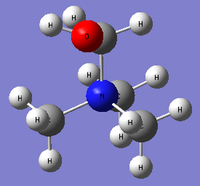Initial optimisation was based on the default setting when drawing in Gaussview which gave a structure with dihedral angle of H-O-C-N= 180.0° as shown in Figure 14. However, while the forces and displacements have been successfully converged in the optimisation step, the frequencies obtained are much above ±15 cm^-1 and there is a negative frequency at -122 cm^-1 which suggests a maximum peak along the potential energy surface i.e. a transition state but not a true energy minimum.

Low frequencies --- -121.5225   -3.2349    0.0005    0.0006    0.0010    3.9361
Low frequencies ---    5.0490  129.6657  217.5142

A structure was redrawn with dihedral angle of H-O-C-N= 0.0° and the optimised structure is shown in Figure 15 with optimised dihedral angle of H-O-C-N= 103.9°. This gave the low frequencies which are below ±15 cm^-1 and all frequencies are positive, representing an energy minimum. Its corresponding data are presented below.

Table 31. [N(CH3)3(CH2OH)]+ Optimised with 6-31G(d,p) and tight convergence criteria DOI:10042/27769 File type .log Calculation Type FOPT Calculation Method RB3LYP Basis Set 6-31G(d,p) Charge 1 Final Energy/ a.u. -289.39470724 Gradient 0.00000043 Dipole Moment/ Debye 2.14 Point Group C1 Calculation time 58 min 55.4 sec

Item Value Threshold Converged? Maximum Force 0.000000 0.000015 YES RMS Force 0.000000 0.000010 YES Maximum Displacement 0.000025 0.000060 YES RMS Displacement 0.000007 0.000040 YES Predicted change in Energy=-8.859765D-12 Optimization completed. -- Stationary point found. ----------------------------  ! Optimized Parameters  !  ! (Angstroms and Degrees)  ! -------------------------- --------------------------  ! Name Definition Value Derivative Info.  ! --------------------------------------------------------------------------------  ! R1 R(1,2) 1.5038 -DE/DX = 0.0  !  ! R2 R(1,6) 1.5092 -DE/DX = 0.0  !  ! R3 R(1,10) 1.5044 -DE/DX = 0.0  !  ! R4 R(1,14) 1.5528 -DE/DX = 0.0  !  ! R5 R(2,3) 1.0902 -DE/DX = 0.0  !  ! R6 R(2,4) 1.0908 -DE/DX = 0.0  !  ! R7 R(2,5) 1.0907 -DE/DX = 0.0  !  ! R8 R(6,7) 1.0905 -DE/DX = 0.0  !  ! R9 R(6,8) 1.0887 -DE/DX = 0.0  !  ! R10 R(6,9) 1.0901 -DE/DX = 0.0  !  ! R11 R(10,11) 1.089 -DE/DX = 0.0  !  ! R12 R(10,12) 1.0912 -DE/DX = 0.0  !  ! R13 R(10,13) 1.09 -DE/DX = 0.0  !  ! R14 R(14,15) 1.0929 -DE/DX = 0.0  !  ! R15 R(14,16) 1.0942 -DE/DX = 0.0  !  ! R16 R(14,17) 1.3736 -DE/DX = 0.0  !  ! R17 R(17,18) 0.9668 -DE/DX = 0.0  ! Forces and displacements are successfully converged. The optimised N-C1 bond length (where C1 is not attached to O) is 1.50 Å, N-C2 bond length (where C2 is attached to O) is 1.55 Å and C-H bond length is 1.09 Å. Average C-N-C bond angle is 109.5± 0.7° which corresponds to a tetrahedral structure around the central heteroatom N. Although one of the four substituent is methoxy instead methyl, the steric bulk around N is similar and hence to minimise steric clash, the best geometry for [N(CH3)3(CH2OH)]+ to adopt is tetrahedral.

Table 32. [N(CH3)3(CH2OH)]+ Frequency Analysis DOI:10042/27770 File type .log Calculation Type FREQ Calculation Method RB3LYP Basis Set 6-31G(d,p) Charge 1 Final Energy/ a.u. -289.39470724 Gradient 0.00000043 Dipole Moment/ Debye 2.14 Point Group C1 Calculation time 27 min 9.8 sec

Low frequencies --- -8.4244 -5.0137 -1.0425 -0.0012 0.0001 0.0005 Low frequencies --- 131.1075 213.4651 255.7117 Low frequencies are below ±15 cm-1 and all 'real' frequencies are positive, representing an energy minimum.

[N(CH₃)₃(CH₂CN)]⁺

Table 33. [N(CH3)3(CH2CN)]+ Optimised with 6-31G(d,p) and tight convergence criteria DOI:10042/27805 File type .log Calculation Type FOPT Calculation Method RB3LYP Basis Set 6-31G(d,p) Charge 1 Final Energy/ a.u. -306.39376383 Gradient 0.00000076 Dipole Moment/ Debye 5.76 Point Group C1 Calculation time 25 min 30.8 sec

Item Value Threshold Converged? Maximum Force 0.000001 0.000015 YES RMS Force 0.000000 0.000010 YES Maximum Displacement 0.000055 0.000060 YES RMS Displacement 0.000021 0.000040 YES Predicted change in Energy=-3.242231D-11 Optimization completed. -- Stationary point found. ----------------------------  ! Optimized Parameters  !  ! (Angstroms and Degrees)  ! -------------------------- --------------------------  ! Name Definition Value Derivative Info.  ! --------------------------------------------------------------------------------  ! R1 R(1,2) 1.5139 -DE/DX = 0.0  !  ! R2 R(1,6) 1.5116 -DE/DX = 0.0  !  ! R3 R(1,10) 1.5139 -DE/DX = 0.0  !  ! R4 R(1,14) 1.5264 -DE/DX = 0.0  !  ! R5 R(2,3) 1.0897 -DE/DX = 0.0  !  ! R6 R(2,4) 1.0897 -DE/DX = 0.0  !  ! R7 R(2,5) 1.0905 -DE/DX = 0.0  !  ! R8 R(6,7) 1.0904 -DE/DX = 0.0  !  ! R9 R(6,8) 1.0904 -DE/DX = 0.0  !  ! R10 R(6,9) 1.0897 -DE/DX = 0.0  !  ! R11 R(10,11) 1.0905 -DE/DX = 0.0  !  ! R12 R(10,12) 1.0897 -DE/DX = 0.0  !  ! R13 R(10,13) 1.0897 -DE/DX = 0.0  !  ! R14 R(14,15) 1.0935 -DE/DX = 0.0  !  ! R15 R(14,16) 1.0935 -DE/DX = 0.0  !  ! R16 R(14,17) 1.4599 -DE/DX = 0.0  !  ! R17 R(17,18) 1.1596 -DE/DX = 0.0  ! Forces and displacements are successfully converged. The optimised N-C1 bond length (where C1 is not attached to O) is 1.51 Å, N-C2 bond length (where C2 is attached to O) is 1.53 Å and C-H bond length is 1.09 Å. Average C-N-C bond angle is 109.5° which corresponds to a tetrahedral structure around the central heteroatom N. Although one of the four substituent is nitrile instead methyl, the steric bulk is similar and hence to minimise steric clash, the best geometry for [N(CH3)3(CH2CN)]+ to adopt is tetrahedral.

Table 34. [N(CH3)3(CH2CN)]+ Frequency Analysis DOI:10042/27806 File type .log Calculation Type FREQ Calculation Method RB3LYP Basis Set 6-31G(d,p) Charge 1 Final Energy/ a.u. -306.39376383 Gradient 0.00000088 Dipole Moment/ Debye 5.76 Point Group C1 Calculation time 30 min 39.6 sec

Low frequencies --- -2.5692 -0.0009 -0.0007 -0.0004 7.1671 9.6826 Low frequencies --- 91.7790 154.0318 210.9372 Low frequencies are below ±15 cm-1 and all 'real' frequencies are positive, representing an energy minimum.

Population Analysis

Table 35. [N(CH3)3CH2OH]+ Population Analysis DOI:10042/27807 File type .log Calculation Type SP Calculation Method RB3LYP Basis Set 6-31G(d,p) Charge 1 Final Energy/ a.u. -289.39471218 Dipole Moment/ Debye 2.14 Point Group C1 Calculation time 1 min 2.7 sec

Table 36. [N(CH3)3CH2CN]+ Population Analysis DOI:10042/27808 File type .log Calculation Type SP Calculation Method RB3LYP Basis Set 6-31G(d,p) Charge 1 Final Energy/ a.u. -306.39377031 Dipole Moment/ Debye 5.76 Point Group C1 Calculation time 1 min 14.7 sec

NBO

Table 37. Comparison of NBO
Molecule	[N(CH3)4]+		[N(CH3)3CH2OH]+ (OH=EDG)		[N(CH3)3CH2CN]+ (CN=EWG)
Colour range
Charge distribution by colour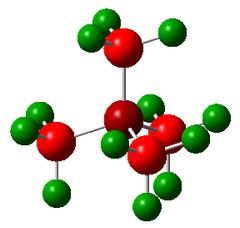
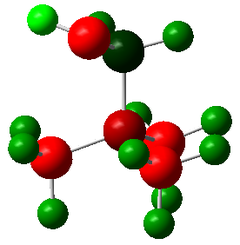
Charge shown in numbers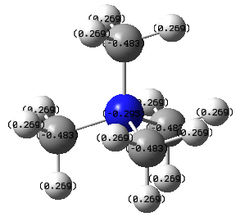
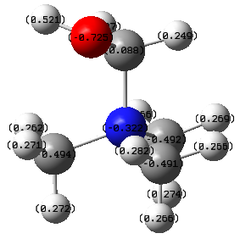
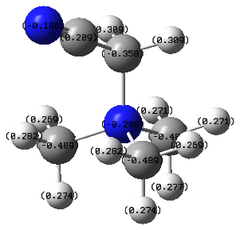
Tabulated X-C average charges where C is attached to functional groups where applicable	N	C	N	C	N	C
	-0.295	-0.483	-0.322	+0.088	-0.289	-0.358

With reference to methyl group in [N(CH₃)₄]⁺, OH is an electron donating substituent while CN is an electron withdrawing substituent, hence the central atom N will have a higher electron density in [N(CH₃)₃CH₂OH]⁺ and a lower electron density in -[N(CH₃)₃CH₂CN]⁺. This matches with the data where the sum of charge of the substituent i.e. -CH₃ in [N(CH₃)₄]⁺, -CH₂OH in [N(CH₃)₃CH₂OH] and -CH₂CN in [N(CH₃)₃CH₂CN] is +0.324, +0.370 and +0.284 respectively. This means equal and opposite effect on the adjacent N i.e. -0.324, -0.370 and -0.284 respectively. The same order is observed in the actual charge on N when the rest of the three methyl groups and positive charge delocalisation are taken into account with N= -0.295 (methyl as reference), -0.322 (more negative as N gains electron density from electron-donating CH₂OH fragment) and -0.289 (more positive as N loses electron density to electron-drawing CH₂CN) respectively, as shown in Table 37. Note: the entire substituent fragment i.e. including -CH₂- must be taken into account in electron-donating or withdrawing effect as summing the charge of OH or CN only cannot account for the trend in N's charge.

For the C directly attached to OH, although it is attached to the electron-donating OH, it is rather electron deficient with charge= +0.088, hence the electron donating effect is not acting on this C. Instead, since the C is between two very electronegative atoms, O and N, its electron density is withdrawn to a significant extent.
For the C directly attached to CN, although it is attached to the electron-withdrawing CN, its electron density is not as low as expected with charge= -0.358. Instead, the more electronegative central N is even more electron deficient than this methylene C when it is expected to have a greater electron density due to ability to pull electron towards itself. Hence, the electron withdrawing effect of CN is really acting on the central N instead of the adjacent methylene C. Also, as the methylene C is only attached to one electronegative atom N now, it is less electron deficient and it can also potentially withdraw electron from the adjacent more electropositive hydrogens.

MO

Table 38. Comparison of MO
Molecule	[N(CH3)4]+	[N(CH3)3CH2OH]+	[N(CH3)3CH2CN]+
LUMO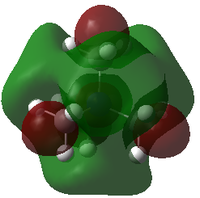
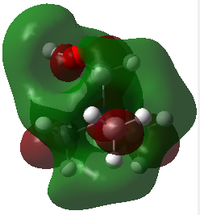
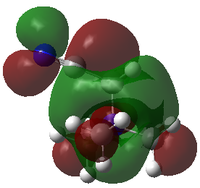
LUMO Energy/ a.u.	-0.13302	-0.12459	-0.18183
HOMO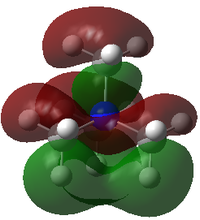
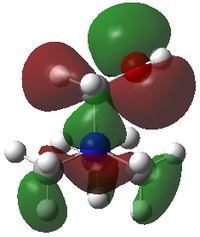
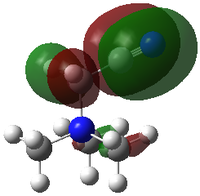
HOMO Energy/ a.u.	-0.57934	-0.48763	-0.50048
HOMO-LUMO energy difference/ a.u.	0.44632	0.36304	0.31865

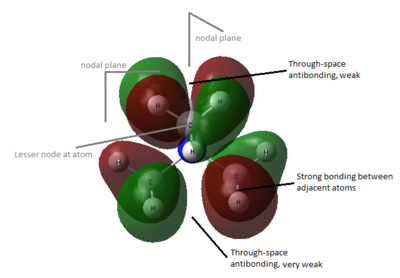
• LUMO

The shape of LUMO of the three molecules are similar. There are many weak through-space bonding interactions between the 2p orbitals of all C (green region). Although there is a node on C but as the node is on atom, its antibonding character is not strong. There are also some weak through-space antibonding interaction between the other half of 2p orbital of C (red)/2s orbital of N (red) and the rest of the MO (green) . The shape of LUMO has changed to allow electron density to be delocalised into the functional group, OH or CN, for bonding and anti-bonding interaction.
In [N(CH₃)₃CH₂OH]⁺, although bonding interaction has been extended to allow electron density to flow from the central nitrogen to oxygen, the node at oxygen also creates much more through-space anti-bonding interaction, hence raising the energy of LUMO from -0.13302 to -0.12459.
In [N(CH₃)₃CH₂CN]⁺, there is additional strong through-space bonding extended to the C of nitrile group. Although there are nodes at C and N of nitrile, this is essentially a π* orbital of CN, which are normally not very strongly antibonding, with the side on C bonding with the rest of the MO. Overall, the stronger bonding interaction lowers the LUMO energy.

• HOMO

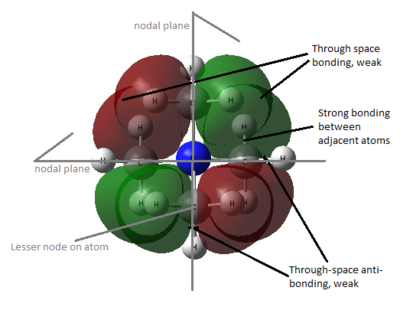
The electron density becomes less delocalised into the -N(CH₃)₃ fragment and is more localised on the substituent as which is changed from Me to CH₂OH to CH₂CN.
In [N(CH₃)₄]⁺, there is strong bonding interaction between 2p orbitals of N and C, which extends to 1s orbitals of some H atoms. There is antibonding interaction across the p orbitals of N and C due to node on these atoms. In this case, the MO is delocalised over almost the whole molecule.
In [N(CH₃)₃CH₂OH]⁺, although the antibonding interaction within OH is not strong as nodes are on the atom across the p-orbital of O, there is very strong antibonding interaction between adjacent atoms, methylene C and O, hence raising the energy of HOMO significantly.
In [N(CH₃)₃CH₂CN]⁺, there is least delocalisation of the MO among the three molecules. Any strong bonding interaction between adjacent C-H in methyl, as well as through-space bonding interaction in the -N(CH₃)₃ fragment is minimised and there is strong antibonding interaction between adjacent atoms, methylene C and nitrile C. Although there is also bonding interaction between each phase of p orbitals of C and N of nitrile, this bonding interaction did not compensate the strong antibonding interaction between atoms and weak through-space anti-bonding and overall the HOMO energy also increases.

• Energy

In general, electron withdrawing groups e.g. CN lower the energy of all non-core orbitals including HOMO and LUMO, while electron donating groups e.g. OH raise the energy of all non-core orbitals including HOMO and LUMO.
This trend is well observed in LUMO where the energy level follows the order of -0.18183 (-CH₂CN)< -0.13302 (-Me)< -0.12459 (-CH₂OH).
In HOMO, although the trend agrees for -0.57934 (-Me)< -0.48763 (-CH₂OH), (-CH₂CN) is in the intermediate at -0.50048 instead of the lowest. This is due to electron density localisation on CH₂CN fragment and absence of delocalisation into the -N(CH₃)₃ fragment which leads to loss of much bonding interaction. Hence the HOMO energy of [N(CH₃)₃CH₂CN]⁺ is raised.

Overall, the HOMO-LUMO gap decreases in the order of 0.44632 (-Me)> 0.36304 (-CH₂OH)> 0.31856 (-CH₂CN).

• Chemical Impact

1. Reduction (gaining of electrons) depends on the energy level of LUMO. Hence it will be the easiest for [N(CH₃)₃CH₂CN]⁺ to accept electron as its LUMO is lowest in energy, which can better interact with the HOMO of the reductant. Additional electron will be best stabalised. This makes sense in terms of qualitative thinking as electron withdrawing CN makes N more electropositive which is eager to gain electron. In this case, where the additional electron will go into the molecule will likely depend on both charge distribution as studied by NBO as well as electron density as studied by MO. In theory, it will be favourable to land on the most positively charged region due to electrostatic attraction and the less electron density region due to less electronic repulsion, although spatial orbital overlap between the two reactants and hybridisation also complicate things even more and ultimately it is a combination of multiple factors. Note: Calculation of the reduced species (by setting charge=0, spin=doublet) had been attempted to compare the electron density difference and the location of the additional electron but the optimisation (Link to log file) had led to the cleavage of central N- methylene C bond.
2. Oxidation (removal of electrons) depends on the energy level of HOMO. Hence it will be the easiest for [N(CH₃)₃CH₂OH]⁺ to lose electron as its HOMO is highest in energy, which can then overlap better with the LUMO of the oxidant. In this case, oxygen shows both the more negative charge in NBO and reasonable electron density in MO, hence the removal of electron is likely to occur at oxygen. However, as the entire molecule is already positively charged, in reality it will be extremely difficult to oxidise it anymore.
3. Photochemistry Any photochemistry requires the excitation of electron from HOMO to LUMO and this will be the easiest for [N(CH₃)₃CH₂CN]⁺ which has the smallest HOMO-LUMO gap which corresponds to a lower energy wavelength needed. This makes sense as CN has π and π* orbitals whose energy difference is normally smaller than that of σ and σ*. However, 0.31685 a.u. translates to a wavelength of 144 nm which is still too low for a normal photochemistry reaction where a wavelength of >300 nm is preferred to have a suitable lamp source and to avoid overlap with the solvent excitation. Nevertheless, when the molecule is used as solvent (ionic liquid) with suitable counter-anion, this can then prevent solvent excitation and exclusively allows the reactant to be excited, assuming counter-anion does not alter the energy of the cation significantly.

Conclusion

In conclusion, computational chemistry allows us to study the properties and reactivities of ionic liquids, which can be hard to achieve in wet experiments. However, caution needs to be taken as analysis from only one component e.g. NBO or MO is unlikely to produce an accurate prediction and often multiples factors including HOMO-LUMO energy, electron density, hybridisation and charge need to be taken into account for a successful computational chemistry analysis.