Rep:Mod:JLS7211

Introduction

This page is a computational chemistry exercise based on the instructions provided by Henry Rzepa for the Imperial College Year 3 Laboratory course. Numbering of the molecules follows those provided in the instructions for easier reference.

Energy calculation was performed by firstly drawing the structure using Chemdraw, saving it as .cdxml file, optimising the structure further by stretching/twisting the bond while ensuring correct stereochemistry in Avogadro with "force field= MMFF94s" and "algorithm= conjugate gradients". Avogadro was performed in preference to ChemBio3D, despite the latter being faster in energy optimisation, due to real-time energy optimisation process and forces which each atom prefers to move along shown during optimisation. Hence it allows the understanding of how moving a certain atom to certain position/conformation leads to the overall change in energy, rendering a more rational energy optimisation.

NMR simulation for the taxol intermediate was done following an initial energy optimisation of the molecule using Avogadro to generate a Gaussian file with calculation= Geometry optimisation, Theory= B3LYP, Basis= 6-31G(d,p) with solvent= benzene for taxol intermediate and chloroform for all epoxides. Job was run by Imperial College High Performance Computing (HPC) portal and NMR was analysed using GaussView 5.0.9.

Most of the calculated energy values are provided in kcal/mol. This can be easily converted to kJ using 1 kcal= 4.184 kJ for any thermodynamic analysis.

Cyclopentadiene

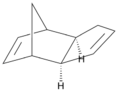
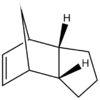
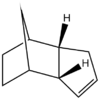
Dimerisation (thermal [4+2] cycloaddtion) of cyclopentadiene monomer

Dimerisation of Cyclopentadiene monomer Diastereoisomers exo endo Energy kcal/mol Stretching (str) 3.38095 3.29873 Angle Bending 29.06626 31.42065 Stretch Bending -1.89926 -1.93753 Out-of-plane Bending 0.01616 0.02381 Torsion (tor) -1.12787 -1.46180 Van der Waals (vdw) 12.63199 12.20842 Electrostatic 12.90735 14.05005 Total 54.97558 57.60232

Scheme 1. Reaction mechanism for dimerisation of cyclopentadiene The endo product is higher in energy than the exo product by 2.63 kcal/mol. However, under normal conditions, the less thermodynamically stable endo product is formed as there is stabilising secondary orbital interaction in the transition state of forming the endo adduct whereas there is no such secondary orbitals interaction in the transition state leading to the exo adduct, as shown in Scheme 1. The endo product is therefore the kinetic product and dimerisation of cyclopentadiene is kinetically controlled. The energy difference between endo and exo is largely due to the increase in angle bending energy (difference= 2.35 kcal/mol) which is the energy involved to bend a bond away from its equilibrium angle. In the endo conformation, the ring, which is formed by joining two adjacent axial position (concave arrangement for the two rings), tends to bend upwards to the equatorial position to minimise steric clash with the other ring and hence causes an increase in angle bending energy. In the exo product, the ring is joined at the equatorial position (linear arrangement for the two rings) and avoids steric clash with the other ring and hence the increase in angle bending energy is significantly less.

Hydrogenation of cyclopentadiene dimer

Hydrogenation of Cyclopentadiene dimer Dihydrogenated product of endo adduct Energy kcal/mol Stretching (str) 3.31117 2.82327 Angle Bending 31.93516 24.68526 Stretch Bending -2.10213 -1.65729 Out-of-plane Bending 0.01318 0.00028 Torsion (tor) -1.46919 -0.37920 Van der Waals (vdw) 13.63802 10.63817 Electrostatic 5.11951 5.14700 Total 50.44572 41.25749

Scheme 2. Reaction mechanism for the hydrogenation of cyclopentadiene dimer The hydrogenated product 4 is lower in energy than 3 by 9.19 kcal/mol. The difference in energy is mainly due to angle bending energy (difference= 7.25 kcal/mol) and to a small extent, vdw energy (difference= 3.00 kcal/mol) due to greater steric repulsion in 3. To explain the large difference in the angle bending energy, geometry of the starting material with 4 sp2 carbons is considered. In general, any sp2 carbon in a ring equal or smaller than 6-membered ring causes instability as 120° favoured by a sp2 centre cannot be geometrically achieved without ring strain. The alkene in the norbornene part of the molecule has sp2 carbons shared by both a 5-membered and a 6-membered ring whereas the sp2 carbons at the other end only causes ring strain to one 5-membered ring. Hence 4 which has less ring strain overall should have more angles close to their equilibrium and hence a lower angle bending energy. 4 should be formed as the thermodynamic product and this hypothesis is confirmed by work done by Skala and Hanika where the first hydrogenation occurs at the norbornene part of the molecule. The hydrogenation of endo dicyclopentadiene is therefore thermodynamically controlled.

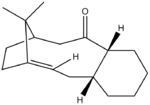
Taxol Intermediate

Atropisomerism

Atropisomerism is a type of stereoisomerism in which the free rotation around a single bond is restricted due to high energy barrier and different conformers can hence be isolated. In the example below, the C-C bonds adjacent to the carbonyl group are restricted from rotating due to constraints imposed by the bridgehead methyl groups as described by Paquette.

Atropisomerism in a key intermediate in the synthesis of Taxol
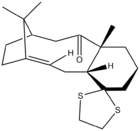
Isomer 9 with C=O pointing up	C=O up (chair)	C=O up (boat)	Isomer 10 with C=O pointing down	C=O down (chair)	C=O down (boat)
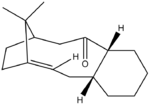
Energy	kcal/mol
Stretching (str)	7.65249	7.93580		7.56127	7.70217
Angle Bending	28.27471	29.91524		18.82556	19.54818
Stretch Bending	-0.07950	-0.00637		-0.13604	-0.07474
Out-of-plane Bending	0.97218	0.97616		0.83645	0.90462
Torsion (tor)	0.31892	3.25529		0.19400	3.49346
Van der Waals (vdw)	33.10146	35.54511		33.32592	35.02188
Electrostatic	0.30722	0.28743		-0.05434	-0.05823
Total	70.54749	77.90867		60.55281	66.53733

Note: Initial attempt to generate the lowerst energy structure in Avogadro had failed and a energy of slightly above 100 kcal/mol was originally obtained. After ensuring the correct substituents, stereochemistry and chair conformation of the cyclohexane ring, it was observed that the four substituents of the bridgehead alkene deviate significantly from a planar geometry. Trying to move the atoms towards a planar arrangement leads to restoration to their original position eventually. After many attempts, pulling the carbonyl oxygen to an extreme position towards the double bond allows the achievement of the lowest energy conformation and the double bond substituents became close to planar.

Atropisomer 10 with the carbonyl group pointing down is lower in energy (difference= 9.99 kcal/mol for chair conformer; 11.4 kcal/mol for boat conformer) and therefore more stable than 9 with carbonyl group pointing up. The lowering of energy is mainly attributed to the angle bending energy e.g. difference= 9.45 kcal/mol for chair conformation of 9 and 10, approximately 95% contribution to total energy difference. This indicated that the bond is closer to the equilibrium angle in the the chair conformer of 10 than that of 9. For instance,

• O-C1-C2 bond angle= 121° for chair conformer of isomer 10 but 117° for chair conformer of isomer 9 (where C1 is the carbonyl carbon, C2 is the carbon in the cyclohexane ring and is adjacent to C1, compared to equilibrium angle= 120° for trigonal planar arrangement;
• C1-C2-H bond angle= 106° for chair conformation of isomer 10 but 100° for chair conformation of isomer 9 (where C1 and C2 are the same atom as above and H is the hydrogen directly attached to C2, compared to equilibrium angle= 109° for tetrahedral arrangement.

A full analysis would involve calculation of all the bond angles and statistical analysis of their deviations from the equilibrium angles.

It was concluded by Maier and Schleyer that double bond joint to a bridgehead is particularly stable (termed "hyperstable") due to its "cage structure" and its corresponding hydrogenated product will experience more strain, which is confirmed by higher calculated energy of 69.53391 kcal/mol. Hence, the bridgehead alkene reacts slowly.

Boat conformation for either atropisomer is less stable than the corresponding chair conformation. The increase in energy is attributed to not only angle bending and Van der Waals energy but also a relative large increase in the torsional energy as some substituents of the cyclohexane ring become eclipsed in the boat conformation.

Spectroscopic Simulation

1. Energy Optimisation

Atropisomer of another Taxol intermediate Isomer 18 with C=O pointing down C=O down (chair) C=O down (boat) Energy kcal/mol Stretching (str) 15.00127 14.39233 Angle Bending 30.81057 28.30823 Stretch Bending 0.62615 0.49393 Out-of-plane Bending 0.89618 1.02479 Torsion (tor) 9.76923 13.83543 Van der Waals (vdw) 49.39346 50.55291 Electrostatic -6.05474 -6.39056 Total 100.44212 102.21704

The structure of isomer 18 differs from isomer 10 by a) a methyl group instead of a hydrogen attached to the carbon joining two rings and b) a dithiolane ring attached to the cyclohexane ring. As expected from the trend of isomer 9 and 10 above, isomer 18 with C=O pointing down is more stable than isomer 17 with C=O pointing up (difference= 3.93 kcal/mol for chair conformation and 6.95 kcal/mol for boat conformation). This is consistent with conclusion made by Paquette about relative stability of the two conformers. Within different conformations of cyclohexane ring in isomer 18, just like isomer 10, the boat conformer is higher in energy than the chair conformer. However, the difference is marginal at 1.77 kcal/mol compared to 5.98 kcal/mol for isomer 10. While the major contribution to the increase in energy is from torsional energy (difference= 4.07 kcal/mol) due to the unfavourable eclipsed interaction in the boat conformation, it is interesting to note that the angle bending energy is lower (difference=2.50 kcal/mol) in the boat conformer than the chair conformer, contrary to the trend for isomer 10. This could be possibly due to the zig-zag arrangement from left to right (carbon 1 and 2 to carbon 18 and 19 in the figure shown in Section 3.2.1.) in the boat conformer which seems to be a more natural arrangement than being disrupted by the chair conformation in the chair conformer. Free energy ΔG=-1651.462137 Hartree(Ha) for the chair conformation and =-1651.459536 Ha for the boat conformation. By conversion factor of 1 Hartree= 2625.499 62 kJ/mol, chair conformer is more stable than the boat conformation by 6.83 kJ/mol.

2. Comparing Calculated and Literature values

Fig 1. NMR literature values from Paquette

¹³C NMR:
Chemical shifts are arranged in descending order for both calculated values and literature values and subsequently compared.

¹H NMR:
Limitation: Coupling constants were not in the provided in the literature by Paquette and splitting pattern are often multiplets, hence it is difficult to accurately assign the methylene protons. Coupling constants can in fact be calculated but the process is too time-consuming for this exercise.
Assumptions in treatment of data: (Note: please refer to the figures shown below in the tables for identification of atoms)

1. All methyl protons are in the upfield region with integration of 3.
   
2. δ=1.58 ppm belongs to proton 16 because a) Splitting pattern is shown to be triplet which means that the proton couples to only two other chemically inequivalent protons. Proton candidates that fulfills this criteria around the δ=1.58 region are 33 and 16. However, Proton 33 couples to proton 34 which is two bonds away and proton 26 which is three bonds away. As coupling constants are hugely dependent on the distance between the two coupling protons, it is likely to give two very different coupling constants which give rise to doublet of doublet instead of a triplet. Hence proton 16 which couples to proton 35 and 36 which are both three bonds away is likely to give the triplet (actually overlapped doublet of doublets); b) Change between chair and boat conformations is likely to affect proximal proton 16 rather than proton 33 which is further away. Indeed, proton 16's chemical shift changes significantly between two different conformers (δ=2.54 ppm for chair conformer and δ=1.83 ppm for boat conformer).
   
3. δ=5.21 ppm corresponds to proton 10 which in both conformers is the sole proton with chemical shift in the 5 ppm region.
   
4. After the first 3 assumptions have been made, the rest of the protons were ranked in the order of their chemical shifts. All methylene protons are inequivalent so that they can be treated independently in matching the chemical shifts.

3. NMR Simulation Data

¹³C NMR Simulation

13C NMR Simulation
Conformer	Chair	Boat
DOI	DOI:10042/27431	DOI:10042/27441
Simulated NMR Spectra
Structure with labels
Statistical Analysis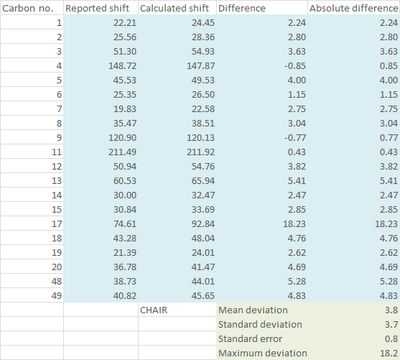
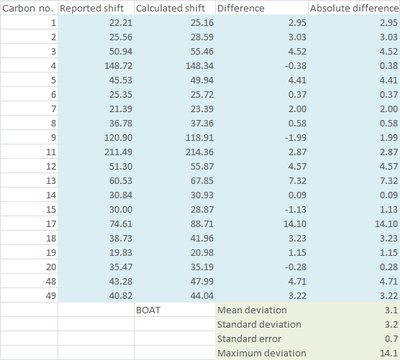
Combined Graphical Analysis

¹H NMR Simulation

1H NMR Simulation
Conformer	Chair	Boat
DOI	DOI:10042/27431	DOI:10042/27441
Simulated NMR Spectra
Structure with labels
Statistical Analysis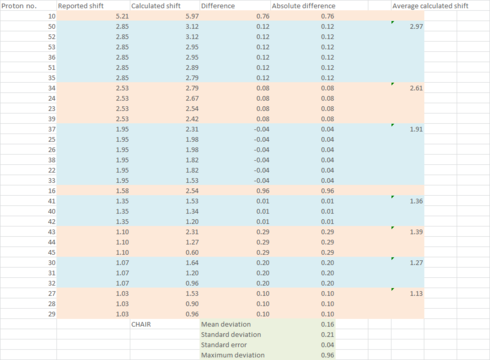
Combined Graphical Analysis

4. Results Analysis

As seen from the statistical and graphical analysis above, mean deviation, standard deviation (and hence standard error) and maximum deviation are all smaller for the boat conformer for both ¹H and ¹³C NMR. The major source of contribution to the larger deviation in the chair conformation comes from the atoms involved in the cyclohexane ring e.g. Carbon 17 and Proton 16. These lead to the conclusion that what was observed by Paquette was actually the less thermodynamically stable boat conformer of 18, even though the product was obtained by refluxing the atropisomer 17 for 5 days, which is equivalent to a thermodynamic reaction condition.

It is also worth noting that calculation for the chair conformer for both ¹H and ¹³C NMR gave a nearly consistent overestimation on the value of chemical shifts. Even for the boat conformer, the overestimation is alleviated but still exists. This can be contributed to heavy atom effect as described by Braddock and Rzepa . In this case, the maximum deviation comes from carbon 17 which is directly attached to two heavy sulfur atoms and hydrogen 16 which is three bonds away from sulfur respectively. Although spin-orbit correction value in response to the heavy atom effect has not been found for sulfur, many corrections reported for heavy halogens have suggested that the corrected value will be lower than the calculated value, hence this might bring the deviation closer to zero.

The Jacobsen and Shi Epoxidation

Crystal Structures of asymmetric epoxidation catalysts

Shi Catalyst

Fig 2. Crystal Structure of the Shi catalyst

In a cyclohexane ring, if a carbon (e.g. C2) is attached to two heteroatoms e.g. oxygen, one (e.g. O6) of which is within the cyclohexane ring and another (e.g. O2) is the substituent, the substituent would prefer the axial position rather than the less hindered equatorial position. This allows anti-periplanar alignment between the lone pair of oxygen (good donor) and the adjacent C-O2 σ* orbital (good acceptor), which leads to stabilising interaction. Consequently, O6 will lose some of its electron density and C-O2 bond will be lengthened as electrons are interacting with its anti-bonding orbital. The anomeric effect can also exhibit in five-membered rings but sometimes to a less extent due to slight deviation from the anti-periplanar alignment.

There are three anomeric centres in the Shi catalyst at C2, C9 and C10 respectively. At C2, C2-O2 (1.423Å) bond are longer than C2-O6 (1.415Å). At C9 and C10, C9-O2(1.454Å) and C10-O4 (1.456Å) are also longer than the adjacent C9-O1(1.423Å) and C10-O5 (1.428Å) respectively. It is interesting to note that even though O1 and O2 looks symmetric around C9 (same for O4 and O5 around C10), only one oxygen's lone pair (O1 for C9, O5 for C10) can anti-periplanarly align to the σ* orbital of the adjacent C-O (O2 for C9, O4 for C10). Otherwise, the mutual anomeric effect would make both adjacent C-O bond length equivalent.

Jacobsen Catalyst

Fig 3. Crystal Structure of the Jacobsen catalyst

Fig 4. Space filling model of the Jacobsen catalyst

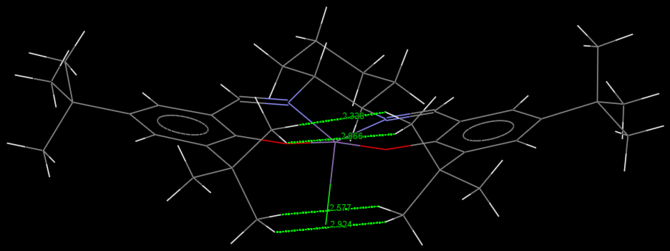
Jacobsen catalyst has a 5-coordinate manganese in the centre. As shown in Figure 3, it has a square pyramidal structure where 4 atoms joint by rings and bridge are on the same plane approximately and a chlorine atom perpendicular to that plane. The entire molecule is close to planar due to delocalisation of electron density of the salen ligands at both sides. The cyclohexane ring adopts the lowest energy chair conformation and produces two stereocentres at the C attached to N, which defines the stereochemistry of the Jacobsen catalyst i.e. (R,R) or (S,S).
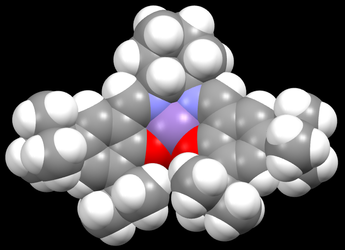
The tert-butyl groups of the salen ligands prevent side-on approach of the alkenes by steric repulsion and this helps to ensure the enantioselectivity of the epoxidation. As shown in the space-filling model in Figure 4, the tert-butyl groups completely block the entrance of any alkene to the catalytic manganese centre (shaded purple) from the side (left, right and bottom of Figure 4. It had been shown by Jacobsen et al. that if the tert-butyl groups is replaced by a smaller methyl group, alkene could have side-on approach to the catalyst. . The two tert-butyl groups in the centre are close together but the interaction between their hydrogens is attractive instead of repulsive, which is also confirmed by NCI simulation later in section 4.5. Maximum attraction for non-bonded hydrogens occurs at 2.4Å and repulsion only occurs below 2.1Å. Two out of the four interactions highlighted in Figure 3. are very close to the attractive interaction of 2.4Å i.e. 2.328Å and 2.577Å. In order to achieve at least one of such attractive interactions, the other pair in the same tert-butyl group has no choice but to be longer than 2.4Å due to the structural constraint, hence weakening the attractive interactions between each of these pairs. Overall, the two tert-butyl groups on each side provides both thermodynamic stability and selectivity of the catalyst.

NMR analysis of epoxides

Epoxides under investigation were energetically optimised by Avogadro and sent for NMR simulation, same as the procedure done for the Taxol intermediate. For full excel analysis of the results, please click (R/S=R-/S- styrene oxide, SR/RS=(S,R)-/(R,S)-dihydronaphthalene oxide). Literature values are obtained from Ji et al.'s work.

Styrene oxide

R- and S-Styrene oxide NMR Simulation
Enantiomer	R-Styrene oxide	S-Styrene oxide
DOI	DOI:10042/27550	DOI:10042/27551
Structure with labels
Simulated 1H NMR Spectra
Analysis of 1H NMR Spectra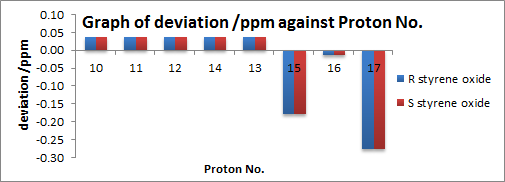
Simulated 13C NMR Spectra
Analysis of 13C NMR Spectra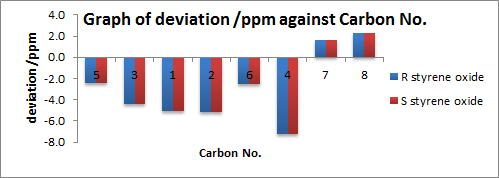

Enantiomers are found to give the same NMR patterns as expected. For ¹H NMR, mean and standard deviations are small i.e. 0.08 and 0.09 respectively. The maximum deviation comes from proton 17. This is probably due to small extent of free rotation of the phenyl ring (although the conformation shown is proven to be most thermodynamically stable by Gaussian calculation) which affects the chemical environment of the spacially proximal 17. There are an overestimation of the calculated values than the literature values for the aromatic region and an underestimation for the aliphatic region.
For ¹³C NMR, the mean and standard deviation are small at 3.8 and 1.9 respectively. However, the maximum deviation is large at 7.2ppm due to carbon 4. Just as the explanation above, this is likely due to some free rotation of the phenyl group. In this case, the chemical shift of carbon ‘’’4’’’ is particular sensitive to changing environment as it is surrounded by many NMR active nuclei. There are an underestimation of the calculated values than the literature values for the aromatic region and an overestimation for the aliphatic region.

Dihydronaphthalene oxide

(S,R) and (R,S)-dihydronaphthalene oxide NMR Simulation
Enantiomer	(S,R)-dihydronaphthalene oxide	(R,S)-dihydronaphthalene oxide
DOI	DOI:10042/27549	DOI:10042/27548
Structure with labels
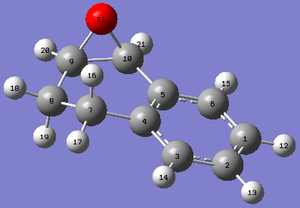
Simulated 1H NMR Spectra
Analysis of 1H NMR Spectra (Numbering corresponds to (S,R))
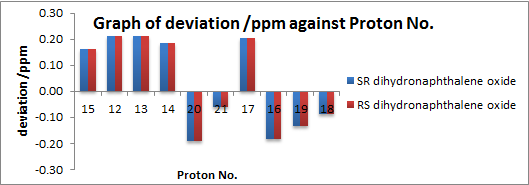
Simulated 13C NMR Spectra
Analysis of 13C NMR Spectra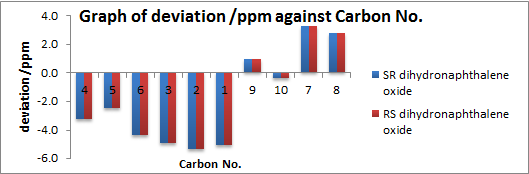

Enantiomers are found to give the same NMR patterns as expected. For ¹H NMR, mean and standard deviations are small i.e. 0.16 and 0.05 respectively. The maximum deviation comes from proton 17 shown in (S,R) (or 16 in (R,S)). Proton 17 is the only proton that is pointing towards the oxygen in the structure. Any deviation e.g. flipping 17 to the equatorial position (with 16 and 19 changing to axial and 18 changing to equatorial has shown to cause deviation in chemical shifts. As oxygen is highly electronegative, the chemical shift of 17 is hence extremely sensitive to the spacial interaction with oxygen. There are an overestimation of the calculated values than the literature values for the aromatic region and an underestimation for the aliphatic region with the exception of 17.
For ¹³C NMR, the mean and standard deviation are small at 3.3 and 1.7 respectively. There are an underestimation of the calculated values than the literature values for the aromatic region and an overestimation for the aliphatic region in general.

Assigning the Absolute Configuration using Optical Rotation

Comparison between literature and calculated values of Optical Rotation
Epoxide	R-Styrene oxide	S-Styrene oxide	(S,R)-dinaphthalene oxide	(R,S)-dinaphthalene oxide
Literature values of Optical Rotation (CHCl3), 589nm	-23.7°, 31°C	+32.1°, 25°C	+133°	-144.9°, 25°C
Calculated values of Optical Rotation (CHCl3) at 25°C, 589nm	-30.14°	+30.41°	+155.81°	-155.82°
DOI	DOI:10042/27470	DOI:10042/27471	DOI:10042/27472	DOI:10042/27476

Note: After gaussian energy optimisation using quantum mechanics, reloading the structure in Avogadro and calculating the energy gave a higher value than before. Hence there is a limitation in using force field optimisation in actually obtaining the lowest energy conformation.

All solvents are chosen to be (CHCl₃) for a fair comparison. In general, the literature values are lower than the calculated values in magnitude as there may not be 100% ee and purity (assumed in calculation) in the literature sample but otherwise there is a close agreement between the two. Temperature can also affect the optical rotation but its effect is difficult to quantify. The optical rotation for (R,S)-dihydronaphthalene oxide was at first obtained to be +35.86° and later realised that in that structure the epoxide oxygen is eclipsed with the vicinal hydrogen which is the unstable conformer. This shows that both the sign and the magnitude of optical rotation is highly sensitive to the overall shape of the molecule.

Relating Transition State to Enantiomeric Excess(trans-β methyl styrene)

The Curtin-Hammett Principle relates the relative concentration of two products to the difference in the transition states for two different conformers of the same molecule, assuming that the conformational interconversion between the two conformers is faster than the reaction towards the corresponding products.

The following steps are followed in the calculating of enantiomeric excess from the given transition state energies.

1. From the given transition state energies within each enantiomer, the lowest energy one is chosen as it represents the most probable pathway for the catalyst to give the corresponding enantiomer.
2. The difference between the lowest transition energy of each enantiomer, ΔG_TS is calculated and converted from the unit used by Gaussian, Hartree to kJ/mol using 1 Ha= 2625.49962 kJ/mol.
3. Gibbs Free Energy of transition state can be related to the K, the ratio of concentration between two enantiomers using
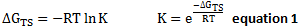
4. The ratio of concentrations of the two species,
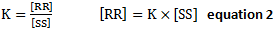
5. Enantiomeric excess,
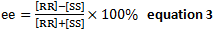
6. Substituting equation 2 into 3,

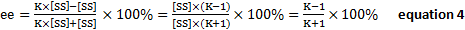
The Shi catalyst

As observed from the structures provided, for the Shi catalyst, there are choices between one of the two oxygen in the dioxirane (O1 or O2 in Figure 5), as well as whether the orientation of alkene’s phenyl group with respect to fructose can be endo or exo. This gives 2²=4 possibilities for each enantiomer.

Calculation of Enantiomeric Excess from Transition State Free energies
Free Energy of Transition State for (R,R)-Trans-β-methyl Styrene Oxide Formation	-1343.022970	-1343.019233	-1343.029272	-1343.032443
Free Energy of Transition State for (S,S)-Trans-β-methyl Styrene Oxide Formation	-1343.017942	-1343.015603	-1343.023766	-1343.024742
ΔGTS	-1343.032443-(-1343.024742) =-0.007701 Ha =-20.21897257 kJ/mol =-2.021897257 x 104 J/mol
K using equation 1	3499.272792
ee using equation 4	99.94%

From the table above, epoxidation of Trans-β-methyl Styrene with the Shi catalyst is calculated to be highly enantiomeric selective and (R,R)-Trans-β-methyl Styrene Oxide is the major product with ee=99.94%. The calculated ee has a fair agreement with literature values of 93.2 % ee of (R,R) over (S,S) at 20°C (Temperature for calculation=298.15K= 25°C)

Fig 5. Lowest transition state energy of the Shi catalyst epoxidation on trans-β methyl styrene

Fig 6. NCI of the transition state of the Shi catalyst epoxidation on trans-β methyl styrene

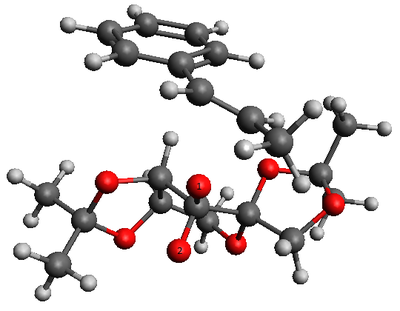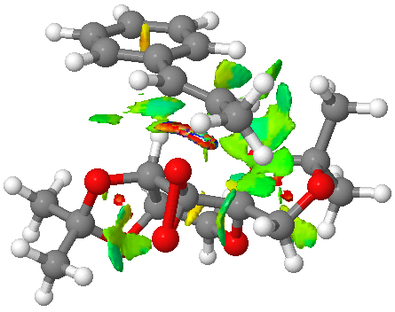The lowest energy transition state corresponds to the endo alignment of the methyl styrene's phenyl ring and the fructose of the Shi catalyst. As discussed in the example of cyclopentadiene dimerization earlier, the endo alignment allows stabilising secondary orbital interaction. O1 is favoured over O2 as the transferring atom to allow favourable van der waals interaction (attractive interaction shown in green in Figure 6 between the substrate and the upward pointing methyl group of the Shi catalyst. By examining all the transition state structures, all the transition state with O1 as the transferring atom is lower in energy than O2 being the transferring atom. This shows the significant contribution in the van der waal's attraction as the stabilising factor to the transition state.

In theory, the epoxidation should be even more enantiomeric selective as the second lowest transition state energy (-1343.029272 Ha) also leads to the (R,R) product. However, the reported value is lower possibly because firstly, the calculation was done in solvent=water whereas the actual reaction was done in organic/salt solution mixture. Solvent effects in terms of polarity and hydrogen bond formation ability will affect the transition state energy and cause deviation between the calculated and the literature values. Secondly, a small fraction of alkene may not have undergone epoxidation by the catalytic pathway and this results in the loss of product enantiomeric selectivity.

The Jacobsen Catalyst

As observed from the structures provided, for the Jacobsen catalyst, methyl styrene's phenyl can align to either salen ligands of the catalyst, resulting in either endo or exo alignment of the phenyl group of the methyl styrene to the phenyl group of the salen ligand, hence there are 2¹=2 possibilities for each enantiomer.

Calculation of Enantiomeric Excess from Transition State Free energies
Free Energy of Transition State for (S,S)-Trans-β-methyl Styrene Oxide Formation	-3383.262481	-3383.257847
Free Energy of Transition State for (R,R)-Trans-β-methyl Styrene Oxide Formation	-3383.253816	-3383.254344
ΔGTS	-3383.262481 -(-3383.254344) =-0.008137 Ha =-21.3637 kJ/mol =-2.13637x 104 J/mol
K using equation 1	5554.228363
ee using equation 4	99.96%

The difference between the transition state energy is due to the fact that in the endo conformation, there is stabilising non-covalent pi stacking between the phenyl ring of methyl styrene and the salen ligand of the catalyst whereas this interaction is absent in the exo alignment. This is due to how the alkene of the substrate must orientate in correct position for oxygen transfer at the Manganese centre and thus affects the alignment of its phenyl group with the catalyst.

There is a large deviation upon comparing the calculated ee value of 99.96% of (S,S) over (R,R) with the 1S experimental ee value of 21.3% with the following possible explanations:
(Note: Suitable literature data for a fairer comparison is unavailable due to different variations in structure and isomer of the catalyst used. Although the absolution configuration for the excess enantiomer has not been identified in experiment 1S by optical rotation due to overly diluted sample, the experimental enantiomeric selectivity is apparently low regardless of the absolute configuration.)

1. Transition state calculations had not taken into account of other possibilities such as the transition state via a metalla-oxacyclobutane and the mechanism for the Jacobsen epoxidation is indeed controversial.
2. Calculation was again done with solvent=water while the actual reaction was performed in organic/salt solution mixture. Temperature was set as 25°C in calculation but the reaction was done at 0°C. Solvent, reaction temperature, catalyst loading, reaction time and the choice of oxidant had been found to all affect ee.
3. Two out of four tert-butyl group is missing in the calculated transition state files provided. This affects the enantiomeric selectivity as the side without tert-butyl group can no longer prevent side-on attack of the alkene to the catalyst.
4. Jacobsen's catalyst is known to be more selective for cis-alkene instead of trans-alkene and hence the enantiomeric selectivity for trans-β methyl styrene decreases.

Non-Covalent Interactions (NCI)

Orbital

Van der waal's interactions can be either attractive or repulsive, which can be investigated using internuclear distance analysis done earlier (Section 4.1) for the crystal structure of the Shi and Jacobsen catalyst. However, it is inconvenient to measure every distance and NCI provides a quicker and visual way of knowing the nature of an interaction. The NCI shown on the left was generated for the most stable transition state for the Jacobsen epoxidation on trans-β methyl styrene. Blue and green represent strong and weak attraction respectively while yellow and red represent weak and strong repulsion respectively. It is observed that the alkene substrate is endo aligned to allow attraction between the phenyl group of the methyl styrene and the phenyl group of the salen ligands, which contributes to the lowering of the transition state energy and enantiomeric selectively. Interestingly, the two phenyl groups are also staggered to avoid any steric repulsion. The attraction between the tert-butyl groups also confirms the earlier conclusion of stabilisation from internuclear distance analysis of the crystal structure.

QTAIM

Using the same transition state, QTAIM allows us to see exactly which two atoms are interacting with each other instead of just an area shown in NCI. The yellow dots in the QTAIM figure on the left represent bond critical points (BCP) where the first derivative of electron density with respect to distance is zero. There are 7 BCPs between the trans-β methyl styrene and the Jacobsen catalyst i.e. between phenyl carbons, between the phenyl hydrogen and the tert-butyl hydrogen, between the benzylic carbon and N of the diimine and between the terminal hydrogen with the hydrogen of the cyclohexane ring (all the first terms refer to that of the methyl styrene while all the second term refers to that of the Jacobsen catalyst). A limitation is that QTAIM is not able to tell whether the interactions are attractive or repulsive and NCI complements this to show that these are indeed the cooperative attractive interactions which stabilise the transition state. The relative distance of BCP between two atoms is observed to be different for phenyl C-H. BCP is further away from the more electronegative atom i.e. C as the greater electron density means steeper electron density gradient and thus it extends for a longer distance along the bond before the gradient reaching zero. This concept can subsequently be exploited to investigate the acidity of hydrogens: BCP closer to hydrogen suggests greater acidity of the hydrogen which would want to leave as a proton with little electron density.

Suggested epoxide

Stereoisomers of the suggested epoxide and its isomers
Epoxide	Suggested 1	Diastereoisomer 2	Enantiomer 3
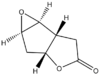
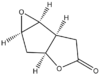
Calculated energies/ kcal/mol	9.84588	8.69922	9.84419
Literature values of Optical Rotation	+125° (CHCl3) at 22°C	not reported	-108°(CHCl3)
Calculated values of Optical Rotation	+121.75°(CHCl3) at 25°C	+59.28°(CHCl3) at 25°C	-121.75°(CHCl3) at 25°C
DOI	DOI:10042/27547	DOI:10042/27546	DOI:10042/27545

The suggested epoxide 1 can be synthesised in high yield (82%) with relatively straight forward reagent and procedure from its corresponding alkene. Only one literature value for either 1 or its enantiomer 3 is available while no optical rotation value has been reported for its diastereoisomer 2. Without the ability to cross-reference with other literature data, there is definitely a need to confirm the optical rotation value by computation. The diastereoisomer with epoxide formed at the opposite side from the suggested epoxide is calculated to be of even lower in energy as the epoxide oxygen isn't eclipsed with hydrogen. Hence the probability of formation of this diastereoisomer requires investigation.
The calculated value for 1 is +121.75° which is in close agreement with the literature value of +125°. 2 has an even lower optical rotation value and therefore its formation is unlikely. The calculated value of -121.75° for the enantiomer 3 also closely agrees with the literature value of -108°.