Rep:Mod:JK21056

Task 6: Dynamical Properties and the Diffusion Coefficient

Task 1

Using data from simulation

For the following graphs, the series Timestep was replaced by Time, which was achieved by multiplying Timestep series by a tenth of the simulation timestep (0.002).

Figure 1: Mean Squared Displacement of the gas as a function of Time. The gradient of the linear section = 1.41

Figure 2: Mean Squared Displacement of the liquid as a function of Time. The gradient of the line = 0.0509

Figure 3: Mean Squared Displacement of the solid as a function of Time. The gradient of the line is assumed to be zero at equilibrium.

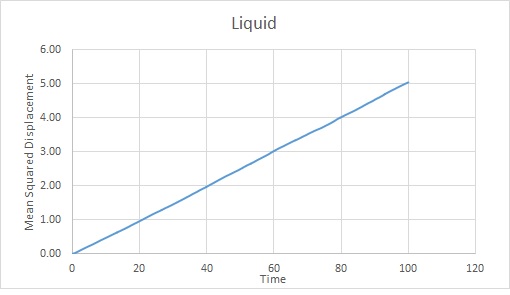
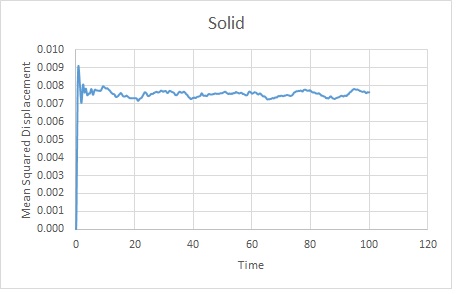
The trends are as expected. The gas becomes the most displaced as it is the most disordered phase. The rate of change of displacement increases until about timestep 2000. This is probably because the gas has diffused sufficiently to overcome Lennard Jones Potential at this point. It will continue to diffuse.

The liquid becomes more diffuse with time but at a much slower rate than the gas because it has stronger interactions between particles.

The solid rapidly takes its lattice position as this is energetically favourable. It will oscillate slightly before remaining in the lattice. Although there is a slight translation, the scale shows that this is very small so the position varies very little from its average.

Estimation of $D$, the Diffusion Coefficient:

$D=\frac{1}{6}\frac{\partial ⟨r^2\left(t\right)⟩}{\partial t}$

Using the gradients of the linear sections of the graphs, as mentioned above:

Gas: $D=\frac{1}{6}\times 1.41=0.235$ Reduced units

Liquid: $D=\frac{1}{6}\times 0.0509=0.00848$ Reduced units

Solid: $D=\frac{1}{6}\times 0=0$ Reduced units

Data from one million atom simulations

Time could not be calculated as the simulation's timestep was not given:

Figure 4: Mean Squared Displacement of the gas as a function of Timestep. The gradient of the linear section = 0.0376

Figure 5: Mean Squared Displacement of the liquid as a function of Timestep. The gradient of the linear section = 0.00105

Figure 6: Mean Squared Displacement of the solid as a function of Timestep. The gradient of the line is assumed to be zero at equilibrium.

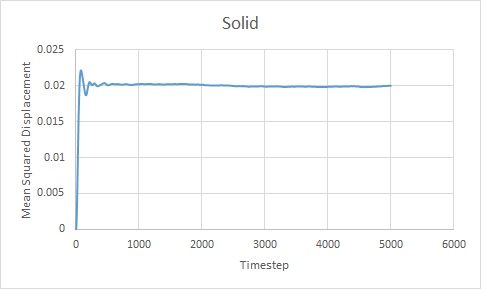
Using the gradients of the linear sections of the graphs, as mentioned above:

Gas: $D=\frac{1}{6}\times 0.0376=0.00627$ Unknown units

Liquid: $D=\frac{1}{6}\times 0.00105=0.000175$ Unknown units

Solid: $D=\frac{1}{6}\times 0=0$ Unknown units

Task 2

Evaluating the normalised velocity autocorrelation function for a 1D harmonic oscillator:

Figure 7: VACF evaluation

Figure 8: VACF evaluation part 2

Figure 9: The VACF for a harmonic oscillator, solid and liquid plotted for timesteps 0 to 500.

Task 3

The trapezium rule was used to evaluate the area beneath the graphs for my own simulation. This gave an integration of -5.39 for the solid, -5.39 for the liquid and 3499 for the gas. The diffusion coefficient, $D$ was calculated in each case: $D_{solid}=\frac{1}{3}\times -5.39=-1.80$

$D_{liquid}=\frac{1}{3}\times -5.39=-1.80$

$D_{gas}=\frac{1}{3}\times 3499=1166$

Figure 9: Running integration using the trapezium rule for solid and liquid. The two integrations overlap.

Figure 10: Running integration using the trapezium rule for gas.