Section 3: Equilibration

Task 1

Generating atoms in random positions will place them in situations in which they wouldn't naturally be found. The simulation is therefore deviating from reality. For example, two atoms could be generated very close to each other, a configuration which has very high energy and will give an imperfect simulation.

Task 2

Satisfying that the lattice spacing and density match:

$D e n s i t y = \frac{N}{V}$

Here the volume is the lattice spacing cubed, while the number of atoms equals one in the unit cell.

$D e n s i t y = \frac{1}{1.0772 2^{3}} = 0.800$

Now we are considering a face-centred cubic lattice with a lattice point number density of 1.2. There are four atoms per unit cell, therefore:

$1.2 = \frac{4}{(s i d e l e n g t h)^{3}}$

So:

$S i d e l e n g t h = 1.49$

Task 3

4000 atoms would be created in the face-centred cubic lattice because each unit cell contains 4 atoms.

Task 4

'mass 1 1.0' means set the mass of atom type 1 to 1.0 in reduced units.

'pair_style lj/cut 3.0' sets the interactions between pairs of atoms. lj/cut means set Lennard-Jones interactions for atoms beyond a distance of 3.0 to 0. This function does not compute a Coulombic interaction.

'pair_coeff * * 1.0 1.0' This is setting the coefficients in the Lennard-Jones potential equation. The asterisks mean apply the following coefficients to all atom types. The first 1.0 sets $ϵ = 1.0$ and the second 1.0 sets $σ = 1.0$ , both in energy units.

Task 5

We will use the Verlet algorithm.

Task 6

*Figure 1:* Energy against time for the timestep 0.001

*Figure 2:* Temperature against time for the timestep 0.001

*Figure 3:* Pressure against time for the timestep 0.001

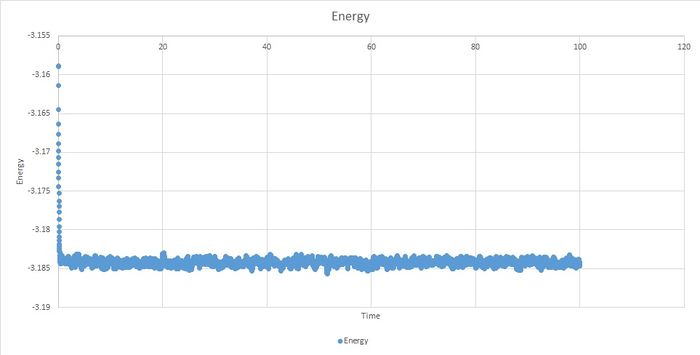
The system reaches equilibrium, within the boundaries $t = 0.3$ and $t = 0.4$ .

*Figure 4:* Energy vs time for all timesteps. Key: 0.0075 = Blue, 0.0025 = Green, 0.015 = Orange, 0.01 = Yellow, 0.001 = Grey

The best timesteps appear to be 0.001 and 0.0025 because they converge. The larger of these two is 0.0025 so this is the best timestep to use.

Timestep of 0.015 gave particularly bad results. It bears no resemblance to other data and it does not equilibrate.