Rep:Mod:JK2105

Section 2: Introduction to Molecular Dynamics Simulation

Task 1

Figure 1: Analytical is the classical position at time t

Figure 2: Energy is the Velocity-Verlet position at time t

Figure 3: Error is the absolute difference between the two energy calculations at time t

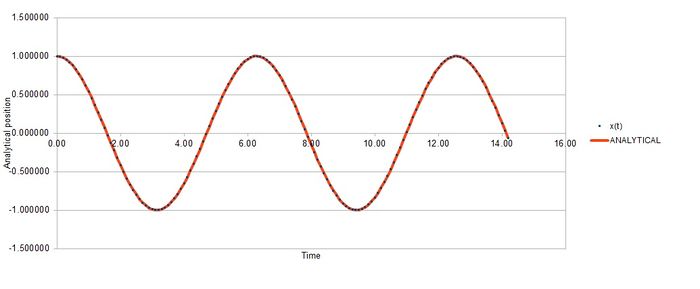
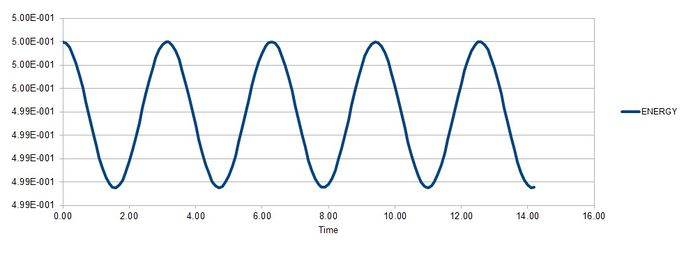
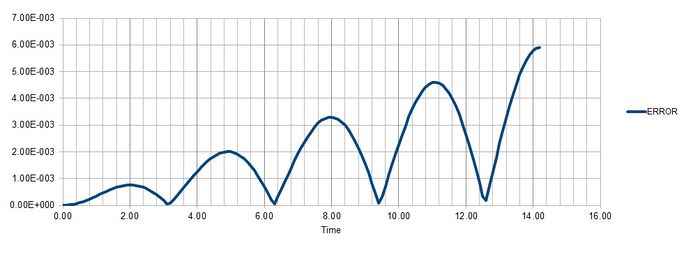
Task 2

Maximum error is found at Time = 2, 4.9, 8, 11.1, 14.2 for timestep 0.1.

Figure 4: Showing the positions of maximum error, fitted with a trend line and function

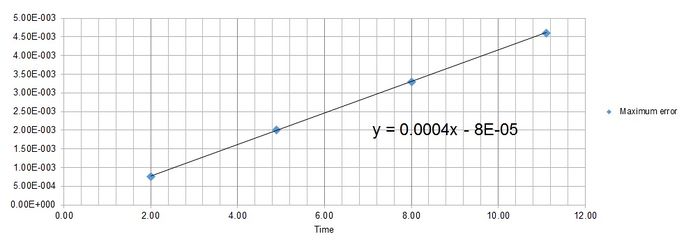
Figure 4 shows the function of the maximum error as $y=0.0004x-8\times 10^{-5}$ where y = error and x = time.

Task 3

The timestep must be less than or equal to 0.2 in order to avoid a change in error greater than 0.005, which is a 1% change. If the energy increases largely, it is an indication that the simulation is incorrect because the total energy of a system experimentally will always want to decrease.

Task 4

Finding the separation, $r_0$, at which the potential energy is 0:

$\varphi \left(r\right)=4ϵ(\frac{{\sigma }^{12}}{r_0^{12}}-\frac{{\sigma }^6}{r_0^6})=0$

Assumed that:

$(\frac{{\sigma }^{12}}{r_0^{12}}-\frac{{\sigma }^6}{r_0^6})=0$

If $r_0=\sigma$ then $(\frac{{\sigma }^{12}}{r_0^{12}}-\frac{{\sigma }^6}{r_0^6})=(1-1)=0$

Therefore $r_0=\sigma$

Next the force was calculated at this separation:

$F=\frac{dv}{dr}=4ϵ(-12\frac{{\sigma }^{12}}{r_0^{13}}+6\frac{{\sigma }^6}{r_0^7})$. Substitute $r_0=\sigma$ to obtain $F=4ϵ-6\sigma$.

Subsequently the equilibrium separation, $r_{eq}$ was calculated:

At equilibrium, $F=\frac{dv}{dr}=4ϵ(-12\frac{{\sigma }^{12}}{r_{eq}^{13}}+6\frac{{\sigma }^6}{r_{eq}^7})=0$.

Assumed that:

$(-12\frac{{\sigma }^{12}}{r_{eq}^{13}}+6\frac{{\sigma }^6}{r_{eq}^7})=0$

And so:

$(2\frac{{\sigma }^{12}}{r_{eq}^{13}}=\frac{{\sigma }^6}{r_{eq}^7})$ so $(2\frac{{\sigma }^{12}}{{\sigma }^6}=\frac{r_{eq}^{13}}{r_{eq}^7})$ so $2{\sigma }^6=r^6$

Substitute back into:

$\varphi \left(r\right)=4ϵ(\frac{{\sigma }^{12}}{r_{eq}^{12}}-\frac{{\sigma }^6}{r_{eq}^6})$

To give:

$\varphi \left(r\right)=4ϵ(\frac{{\sigma }^{12}}{4{\sigma }^{12}}-\frac{{\sigma }^6}{2{\sigma }^6})=4ϵ(\frac{1}{4}-\frac{1}{2})=-ϵ$

This has shown that $ϵ$ is the well depth.

Evaluating the integrals:

$\int \varphi \left(r\right)\mathrm{d}r=4ϵ(\frac{{\sigma }^6}{7r^7}-\frac{{\sigma }^{12}}{13r^{13}})$

$\sigma =ϵ=1.0$

Between $r=2\sigma$ and $r=\mathrm{\infty }$:

$\underset{2\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)\mathrm{d}r=-0.0248$

Between $r=2.5\sigma$ and $r=\mathrm{\infty }$:

$\underset{2.5\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)\mathrm{d}r=-0.00818$

Between $r=3\sigma$ and $r=\mathrm{\infty }$:

$\underset{3\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)\mathrm{d}r=-0.00329$

Task 5

There is 1 mL of water present, which equals 1 g. First, calculate moles:

$Moles=\frac{Mass}{M_r}=\frac{1}{18.0}$

Next, multiply by Avogadro's number to calculate the number of molecules present:

$Numberofmolecules=6.02\times 10^{23}\times \frac{1}{18.0}=3.34\times 10^{22}molecules$

The calculation is reversed to find the volume occupied by 10,000 water molecules:

$\frac{10000}{6.02\times 10^{23}}=1.66\times 10^{-20}moles$

Then to calculate mass:

$Mass=M_r\times Moles=18.0\times 1.66\times 10^{-20}=2.99\times 10^{-19}g=2.99\times 10^{-19}ml$

The simulation clearly models very small volumes.

Task 6

The atom moves to $(0.5,0.5,0.5)+(0.7,0.6,0.2)=(1.2,1.1,0.7)$. Taking into account the Periodic Boundary Conditions, this becomes $(0.2,0.1,0.7)$.

Task 7

Calculating the LJ cutoff in real units: $r^{*}=\frac{r}{\sigma }$

$r^{*}=3.2=\frac{r}{0.34}$

$r=1.088nm$

Calculating the well depth, $ϵ$:

$\frac{ϵ}{k_B}=120K$

Using the Boltzmann Constant: $8.31\times 10^{-3}kJ{K}^{-1}mo{l}^{-1}$

$ϵ=8.31\times 10^{-3}\times 120=0.997kJmo{l}^{-1}$

Calculating the temperature in real units, where $\frac{ϵ}{k_B}=120$:

$T=\frac{T^{*}ϵ}{k_B}=1.5\times 120=180K$