Rep:Mod:JHM
Inorganic Computational Lab
BH3 Modelling
Details of modelling:
Calculation Method: B3LYP
Basis Set: 631_g, dp
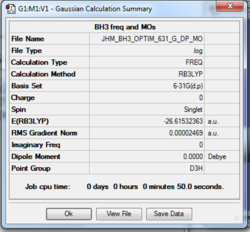
Summary Table
Item table
Item Value Threshold Converged?
Maximum Force 0.000049 0.000450 YES
RMS Force 0.000032 0.000300 YES
Maximum Displacement 0.000196 0.001800 YES
RMS Displacement 0.000128 0.001200 YES
Predicted change in Energy=-1.449838D-08
Optimization completed.
-- Stationary point found.
Log File
Low Frequencies Table
Low frequencies --- -0.2272 -0.0080 -0.0005 22.0746 22.0758 24.0996 Low frequencies --- 1163.1741 1213.2731 1213.2733
Jmol
BH3 Optimisation |
Summary of frequency analysis
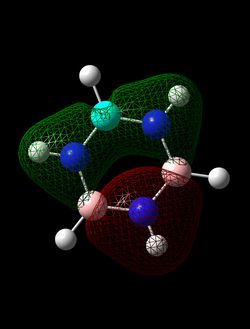
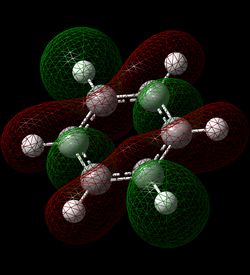
| Wavenumber (cm^-1) | Intensity (arbitrary units) | Symmetry | IR active | Type |
|---|---|---|---|---|
| 1163 | 93 | A1' | Yes | Out of plane bend |
| 1213 | 14 | E' | Slight | Bend |
| 1213 | 14 | E' | Slight | Bend |
| 2582 | 0 | A1' | No | symmetric stretch |
| 2715 | 126 | E' | Yes | Assymetric stretch |
| 2715 | 126 | E' | Yes | Assymetric stretch |
Missing frequency analysis
Certain IR stretches are IR inactive because there is no net change in dipole moment during the vibration, breaking the IR selection rule.
Smf115 (talk) 22:36, 16 May 2018 (BST)Mostly correct but there is an error in one of the assigned symmetries and mention of the degenerate modes is missing.
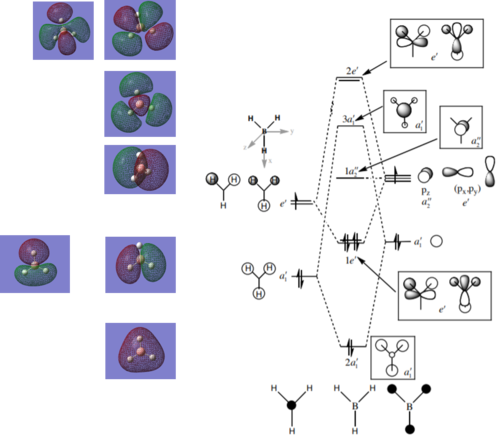
MO Diagram
LCAO diagram for BH3 taken from tutorial problem sheet at http://www.huntresearchgroup.org.uk/teaching/teaching_comp_lab_year2a/Tut_MO_diagram_BH3.pdf, accessed on 01/05/2018.
The LCAO approach produces the correct phases, but the orbitals do not spread over the entire molecule. The change in phase gives the nodes of the computed AOs, however the areas of calculated electron density are skewed away from the LCAO derived orbitals.
The shapes of MO produced by LCAO method are calculated within considerable approximations. The MOs themselves are qualitative solutions to Hartree-Fock equations which assume an independent particle model approximation of the many electron system. Thus electron interactions, which skew the electron density considerably, are neglected in this level of approximation.
NH3 Modelling
Details of modelling:
Calculation Mehtod: B3LYP
Basis Set: 631_g, dp
Summary Table
Item Table
Item Value Threshold Converged?
Maximum Force 0.000006 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000014 0.001800 YES
RMS Displacement 0.000009 0.001200 YES
Predicted change in Energy=-1.141686D-10
Optimization completed.
-- Stationary point found.
Log File
Jmol
NH3 Optimisation |
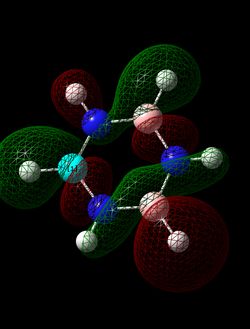
Frequency Analysis
Low frequencies --- -0.0128 0.0015 0.0022 7.1034 8.1048 8.1051 Low frequencies --- 1089.3834 1693.9368 1693.9368
NH3BH3 Modelling
Details of modelling:
Calculation Mehtod: B3LYP
Basis Set: 631_g, dp
Summary Table
Item Table
Item Value Threshold Converged?
Maximum Force 0.000123 0.000450 YES
RMS Force 0.000058 0.000300 YES
Maximum Displacement 0.000515 0.001800 YES
RMS Displacement 0.000296 0.001200 YES
Predicted change in Energy=-1.635696D-07
Optimization completed.
-- Stationary point found.
Log File
Jmol
NH3BH3 Optimisation |
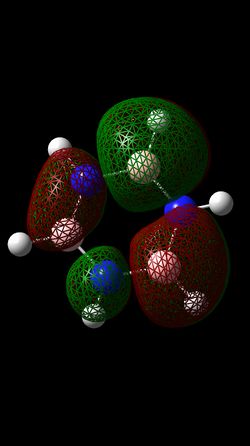
Frequency Analysis
Low frequencies --- -0.0251 -0.0033 -0.0005 17.1178 17.1201 37.1124 Low frequencies --- 265.7770 632.2034 639.3465
Energy Calculations
E(NH3) = -56.5 Eh = -148 kJ/mol
E(BH3) = -26.6 Eh = -65 kJ/mol
E(NH3BH3) = -83.2 = -218 kJ/mol
Association Energʏ
ΔE = E(NH3BH3)-[E(BH3)+E(NH3)] = -0.0515 Eh = -135 kJ/mol
This compares favourably to the DFT calculations used in the following paper:
Covalent and Ionic Nature of the Dative Bond and Account of Accurate Ammonia Borane Binding Enthalpies
Joshua A. Plumley and Jeffrey D. Evanseck*
The Journal of Physical Chemistry A 2007 111 (51), 13472-13483
DOI: 10.1021/jp074937zr
The dative bond is of medium strength, and in the correct ballpark for a bond with a considerable ionic component. It is considerably stronger than an intermolecular force, e.g. H-bonding in water of around 20 KJ/mol, but weaker than a C-C bond of 350 KJ/mol.
BBr3 Modelling
Details of modelling:
Calculation Mehtod: B3LYP
Basis Set: 631_g, (B), LanLDZ (Br) (manually specified pseudopotentials)
Summary Table
DSpace Link
Item Table
Item Value Threshold Converged?
Maximum Force 0.000008 0.000450 YES
RMS Force 0.000005 0.000300 YES
Maximum Displacement 0.000036 0.001800 YES
RMS Displacement 0.000024 0.001200 YES
Predicted change in Energy=-4.086466D-10
Optimization completed.
-- Stationary point found.
Log File
Jmol
BBr3 Optimisation |
Frequency Analysis
Low frequencies --- -0.0137 -0.0064 -0.0046 2.4315 2.4315 4.8421 Low frequencies --- 155.9631 155.9651 267.7052
Project: Aromaticity
Benzene
Parameters
Method: B3LYP
Basis set: 631G, d, p
Summary Table
Item Table
Item Value Threshold Converged?
Maximum Force 0.000194 0.000450 YES
RMS Force 0.000084 0.000300 YES
Maximum Displacement 0.000767 0.001800 YES
RMS Displacement 0.000328 0.001200 YES
Predicted change in Energy=-3.990543D-07
Optimization completed.
-- Stationary point found
Log file
Low Frequencies
Low frequencies --- -16.9682 -14.6636 -14.6636 -0.0056 -0.0055 0.0006 Low frequencies --- 414.1239 414.1239 620.9400
Jmol
BBr3 Optimisation |
Borazine Calculation
Parameters
Calculational level: B3LYP
Basis Set: 631G d,p
Summary Table
Log File
Item Table
Item Value Threshold Converged?
Maximum Force 0.000414 0.000450 YES
RMS Force 0.000174 0.000300 YES
Maximum Displacement 0.000853 0.001800 YES
RMS Displacement 0.000399 0.001200 YES
Predicted change in Energy=-9.378417D-07
Optimization completed.
-- Stationary point found.
Low Frequencies
Low frequencies --- -2.9951 -0.0012 -0.0011 -0.0007 5.8360 8.5180 Low frequencies --- 289.6696 289.8120 404.3662
Jmol
BBr3 Optimisation |
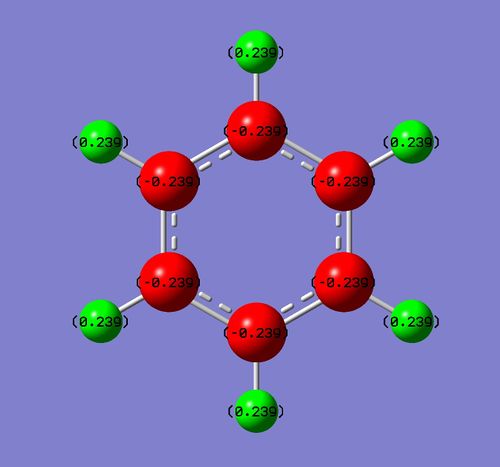
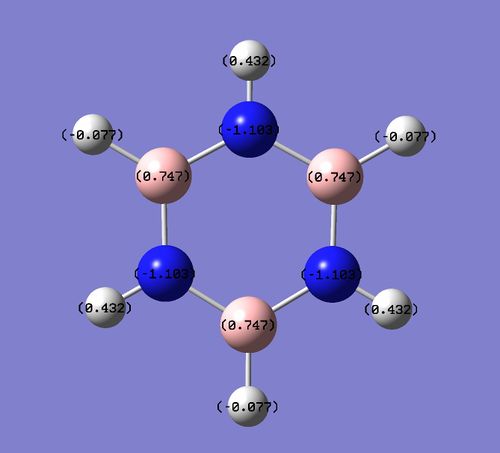
Charge Distribution
Each charge distribution runs on the interval [-1,1]
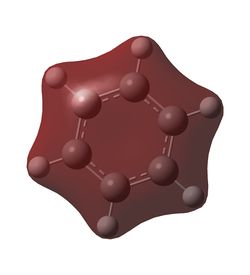
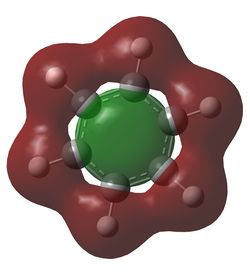
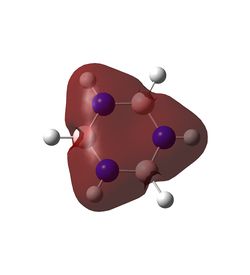
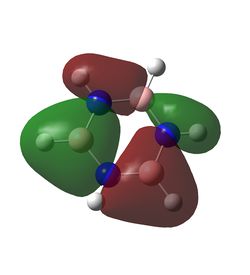
In benzene, each carbon has the same charge density, as does each hydrogen, since they are identical under C6 rotation. In each C-H unit, carbon is slightly more electronegative than hydrogen, adopting a charge of -0.24 Db, and the hydrogen adopts a +0.24 Db charge. The inversion centre of benzene explains why each dipole cancels the equivalent on the opposite side, creating a zero net dipole in benzene.
Borazine exhibits a significant reduction in symmetry compared to benzene, and the difference in electronegativity between boron and nitrogen lead to two different dipoles. Boron, being slightly more electropositive than hydrogen,adopts a partial positive charge of +0.75 Db, whilst the bonded hydrogen adopts a partially negative charge of -0.08 Db. The much more electronegative nitrogen adopts a charge of -1.10 Db and its bonded hydrogen a +0.43 Db charge. Hence each N-H-B-H unit has a net dipole of zero. Since an NH unit is opposite a BH unit across the ring, these dipoles do not cancel each other out, hence borazine has an overall non-zero dipole moment.
Smf115 (talk) 22:33, 16 May 2018 (BST)Good discussion although it would have been good to see the charge distribution highlighted by an equal colour range on both molecules and mention of the neutral charge of the molecules overall.
MO Comparisons
| Benzene MO | Borazine MO | Comments |
|---|---|---|
 |
 |
These two σ orbitals (MO 8) have a nodal plane perpendicular to the plane of the ring. In benzene, this plane intersects carbons para to each other. In borazine, however, this nodal plane is deformed to intersect the centre of the ring and two boron atoms meta to each other. In benzene, all but two protons contribute to the MOs, whereas three hydrogens at the 1,3,5 positions in borazine do not contribute to the MOs. The lobe sizes are equal in carbon and are symmetric by a σ v mirror plane, however in borazine, one lobe (green) extends across two nitrogen atoms, whilst the red lobe is centred on the single remaining nitrogen. |
 |
 |
In MO 19, a bonding σ orbital, there are 4 nodal planes running perpendicular to the plane of the ring. In benzene, the nodes have multiple σ v symmetry planes, whereas the lobes on borazine are less symmetric and are distorted due to the differences in electron density between boron and nitrogen. The lobes are located in the same places as benzene, however. Since each NH unit sits para to a BH group, the orbital components on opposite sides of the borazine ring are of mismatched sizes, with larger contributions from the partially negatively charged hydrogens of the BH unit than NH, as discussed previously. The orbitals that sit between nitrogen and boron are similarly skewed with a larger contribution from the more electronegative nitrogen. |
 |
 |
This antibonding π orbital (MO 22) represents the LUMO of both molecules. In benzene, there exist 4 lobes whose phase alternates moving around the ring and a nodal plane in the plane of the ring. Two of these orbitals cover two carbons each, where the remaining two orbitals spread over only one carbon. Borazine has the same four lobes and phase pattern, however the size of the orbitals is much less regular. There is one large and one small orbital for each of the two types described above (spreading over two and one ring centres respectively). In both molecules, the orbitals do not extend to cover the hydrogens. Interestingly, the orbital lobes that extend over two centres (B and N) in borazine do not vary in size between the two centres, despite the difference in electronegativity which previously caused difference in orbital size |
Smf115 (talk) 22:38, 16 May 2018 (BST)Strong MO analysis with nice mention of the symmetry elements
Aromaticity discussion
The MO analysis of benzene gave three bonding and three antibonding π MOs, intermixed with various σ MOs. Each π MO shows a nodal plane in the plane of the ring and lobes extending accross multiple carbon atoms. This gives the notion of charge being delocalised over multiple carbon atoms, leading to a basic picture of aromaticity. MO 17 in particular shows one large lobe above and one below the plane of the ring. This explains the commonly cited criteria for aromaticity such as intermediate bond lengths and increased energetic stability compared to the alkene equivalent. However, MOs 20 and 21 also show more complicated phase patterns of p-orbital overlap, both of which contribute to the delocalised electron cloud above and below the ring.
The p-orbital overlap picture of aromaticity is, however, insufficient as the σ framework is of key importance to the more detailed picture of aromaticity [1]. Literature suggests that in benzene, π electrons prefer to localise, whilst σ electrons prefer to delocalise. Hence the idea of equivalent intermediate bonding is in fact not an effect of p-orbital electron delocalisation but of the σ framework. This notion is in qualitative agreement with the MOs calculated, and can be employed to understand the relative aromatic resonance energy of benzene and borazine. If we assume that the relative number of delocalized sigma MOs for each molecule gives an indication of the relative contribution of the sigma framework, we can see that in benzene 2 MOs (7 and 12) contribute to a delocalised sigma framework, whereas in borazine, only MO 7 contributes to this framework. This reduced component of sigma framework explains the reduced resonance energy of borazine compared to benzene.
Analysis of the log files and the coefficients of the basis sets for the delocalised orbitals show a very symmetric picture for benzene, compared to a much more distorted set of coefficients for borazine. This inconsistency of electron density further contributes to a reduced aromatic resonance stability of borazine compared to benzene
Smf115 (talk) 22:28, 16 May 2018 (BST)Excellent discussion of aromaticity. Great to see reference to the MOs just viewed for benzene and borazine and to supporting literature.
Smf115 (talk) 22:28, 16 May 2018 (BST)Overal an excellent and thorough report.