Rep:Mod:JH1729
Module 1
Week 1
Molecular Mechanics
Cyclopentadiene Dimer and Hydrogenation
The two different forms, exo and endo, of the cyclopentadiene dimer were defined and optimised to confirm the energy differences and hence the most stable form of the dimer. Using an MM2 field for energy minimization the following energy minima were reached:
Exo form of the dimer;
------------MM2 Minimization------------ Note: All parameters used are finalized (Quality = 4). Iteration 108: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 1.2847 Bend: 20.5794 Stretch-Bend: -0.8382 Torsion: 7.6562 Non-1,4 VDW: -1.4169 1,4 VDW: 4.2337 Dipole/Dipole: 0.3775 Total Energy: 31.8765 kcal/mol Calculation completed ------------------------------------ |
 |
Endo form of the dimer;
------------MM2 Minimization------------ Note: All parameters used are finalized (Quality = 4). Iteration 99: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 1.2514 Bend: 20.8445 Stretch-Bend: -0.8362 Torsion: 9.5114 Non-1,4 VDW: -1.5426 1,4 VDW: 4.3213 Dipole/Dipole: 0.4476 Total Energy: 33.9975 kcal/mol Calculation completed ------------------------------------ |
 |
Comparing the final energies of the two calculations shows that the optimised endo dimer is less stable by 2.121 kcal/mol which is a significant difference this energy difference would lead to the exo form being the major product for the dimerisation. However the endo form is preferred due to orbital effects.
The dimer can also be hydrogenated at either of the double bonds leading to two different structures. The structures have been optimised and the energies are given below:
First hydrogenation product;
------------MM2 Minimization------------ Note: All parameters used are finalized (Quality = 4). Iteration 113: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 1.2355 Bend: 18.9359 Stretch-Bend: -0.7610 Torsion: 12.1246 Non-1,4 VDW: -1.5007 1,4 VDW: 5.7293 Dipole/Dipole: 0.1631 Total Energy: 35.9266 kcal/mol Calculation completed ------------------------------------ |
 |
Second hydrogenation product;
------------MM2 Minimization------------ Note: All parameters used are finalized (Quality = 4). Iteration 135: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 1.0978 Bend: 14.5217 Stretch-Bend: -0.5494 Torsion: 12.4981 Non-1,4 VDW: -1.0686 1,4 VDW: 4.5118 Dipole/Dipole: 0.1406 Total Energy: 31.1520 kcal/mol Calculation completed ------------------------------------ |
 |
The total energies of the two species can be compared, this suggests that the second product shown is more stable, by 4.7746 kcal/mol, and hence this is the thermodynamic product for the hydrogenation reaction. The major difference between the component energies is in the bending energy of the two molecules, the first molecule has a bending energy of 18.9359 kcal/mol whereas the second is 4.4142 kcal/mol lower, at 14.5217 kcal/mol, this accounts for most of the stability difference and can be thought of in terms of how close to the bridge the hydrogenation is taking place. When the hydrogenation occurs on the double bond closest to the bridge there is not a large change in the amount of bending modes available as the system is still constrained by the bridge however if the double bond furthest from the bridge is hydrogenated the amount of bending increases.
The stretching energy also slightly disfavours hydrogenation on the more distant double bond but the difference between the two species is small this will again be due to the bridge limiting the movement of the molecule. The torsion energy of the two molecules are very similar, they differ by about 0.4kcal/mol in favour of the first product, this suggests that most of the strain is still in the system which is due to the bridge.
The non-1,4 van der Waals interactions in the systems shows preference for the first system although in both cases the interaction has a negative energy. This suggests that the non-1,4 hydrogens are interacting in beneficial fashion in both systems. The 1-4 interactions give positive contributions in both systems with the energy difference of about 1.2 kcal/mol in favour of the second system, this is the positive interactions of the hydrogens leading to slightly more stabilised species the calculation suggests that this type of interaction is exploited to a greater degree in the second product.
Atropisomerism of an intermediate in the synthesis of Taxol
An intermediate in the synthesis of Taxol has two isomers from two differing positions of the ketone, rotation is possibly to interconvert between the isomers but the energy required is high due to the ring structure of the molecule. Which isomer is formed depends on the stability of the two forms with the more stable form being the major product. Molecular mechanics calculations gives the following energy data when optimising the species geometries:
Carbonyl in plane with the axial alkene proton;
------------MM2 Minimization------------ Warning: Some parameters are guessed (Quality = 1). Iteration 230: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 2.7829 Bend: 16.5403 Stretch-Bend: 0.4299 Torsion: 18.2568 Non-1,4 VDW: -1.5547 1,4 VDW: 13.1093 Dipole/Dipole: -1.7249 Total Energy: 47.8396 kcal/mol Calculation completed ------------------------------------ |
 |
Carbonyl out of plane with the axial alkene proton;
------------MM2 Minimization------------ Warning: Some parameters are guessed (Quality = 1). Iteration 118: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 2.6226 Bend: 11.3362 Stretch-Bend: 0.3431 Torsion: 19.6729 Non-1,4 VDW: -2.1587 1,4 VDW: 12.8697 Dipole/Dipole: -2.0029 Total Energy: 42.6830 kcal/mol Calculation completed ------------------------------------ |
 |
As can be seen from the data above the favoured form is the second isomer with the carbonyl group out of plane with the proton on the alkene which would suggest that this is the preferred product; this priority is mainly due to the bending energy available for the system as the molecule is made from a large ring and for this isomer the two sp2 carbons, on the carbonyl and alkene, create a bend in this ring.
Using MMFF94 calculations leads to the same structure being the most stable but the energies given are much higher with a much greater difference:
Isomer 1:
------------MMFF94 Minimization------------ Iteration 113: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Final Energy: 70.5285 kcal/mol Calculation completed ------------------------------------
Isomer 2:
------------MMFF94 Minimization------------ Iteration 86: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Final Energy: 60.5446 kcal/mol Calculation completed ------------------------------------
Functionalisation of the alkenes proceeds at a much slower rate than expected for a similarly accessible alkene this is because the bicyclic structure is more stable for the alkene[1] at the bridgehead than for the functionalised system with sp3 carbons at the bridgehead. Further research[2] into this suggests that for hydrogenation, which would be one of the simplest reactions to occur, the double bond undergoes isomerisation around the structure to the position with the most substitution before reacting, which would be at the bridgehead, the paper goes on to show through calculation that the olefin strain for the most substituted system is negative and so extremely stable, more stable than the hydrogenated species.
Regioselective Addition of Dichlorocarbene to a diene
Molecular Mechanics
The structure of the diene, right, was optimised by molecular mechanics calculations, MM2, giving the energy in the first section below. The second section shows the MOPAC method which was used to further optimise the structure taking into account electronic and stereoelectronic effects.
------------MM2 Minimization------------ Warning: Some parameters are guessed (Quality = 1). Iteration 131: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 0.6178 Bend: 4.7377 Stretch-Bend: 0.0399 Torsion: 7.6597 Non-1,4 VDW: -1.0699 1,4 VDW: 5.7971 Dipole/Dipole: 0.1123 Total Energy: 17.8945 kcal/mol Calculation completed ------------------------------------ |
 |
------------ Mopac Interface ------------ Model: Untitled-6 Mopac Job: AUX RM1 CHARGE=0 EF GNORM=0.100 SHIFT=80 Finished @ RMS Gradient = 0.08036 (< 0.10000) Heat of Formation = 22.82760 Kcal/Mol -----------------------------------------
The two different optimisation methods give slightly different geometries for the molecule these are explored in the image below:
 |
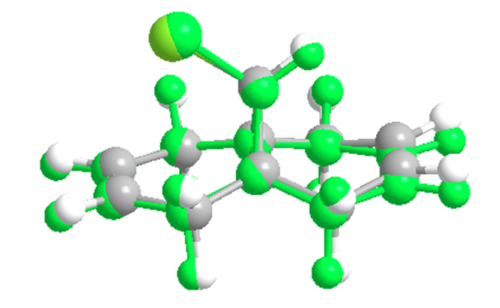| Image of the overlapping dienes highlighting the structural differences, the green structure is the MM2 optimised form |
As can be seen from the image the two structures are almost identical but there are key differences. The overlap of the bridge and chlorine side ring is very good as the structures of these sections very similar between the two with only small variations, 0.02Å or less, in bond lengths and also minor angle discrepancies. The most difference is seen in the other ring with the alkene in this ring shifted up slightly, for the MOPAC structure, as the angle from the bridge to the alkene has changed, for the MM2 optimised structure this angle is 114.4° whereas for the MOPAc structure this is 112.5°.
Molecular Orbitals
A calculation to determine the molecular orbitals of the molecule was performed using Gaussian[3]. Starting with the geometry of the MOPAC optimised molecule the molecular orbital calculation was performed using the B3LYP method and 6-31G basis set, the calculation output file yielded the following HOMO and LUMO orbitals:
|
| ||||||
| HOMO | LUMO |
As can be seen above the HOMO is based mainly on the double bond closest to the chlorine the orbital is quite diffuse being spread across the Cl side of the molecule. Most of the character of this orbital is bonding across the alkene as well as a contribution from the Cl atom (p orbital like).
The LUMO is mostly based on the other alkene, near the proton on the bridge, this is anti bonding across the alkene and has most character on the proton side alkene. There are less diffuse lobes available on the chlorine side which are also anti-bonding. The chlorine again shows p orbital like character but with a different orientation to the HOMO. The chemistry expected here would be attacking into the proton side alkene via a nucleophile to break the double bond as this is the most accessible region of the LUMO.
Electrostatic Potential Surface
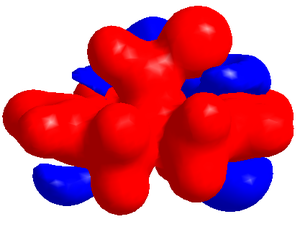
The surface, shown to the right, gives a qualitative view of the potential across the molecule. The ispotential was chosen to show the maximum difference between the two alkenes. As can be seen from the image most of the negative surface is based around the alkenes with the surface being larger closer to the chlorine side, Cl atom is the largest lobe on the bridge, this could be due to the HOMO being based on this region and so electron density will be strongest there.
Vibrational Frequencies of C=C and the effect of nearby C-Cl
The vibrational frequencies were found for the molecule using Gaussian, the calculation was ran on the SCAN system and gave the folling when published [1]. A summary of the calculation is given below:
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| E(RB3LYP) | -887.15337424 a.u. |
| RMS Gradient Norm | 0.0001343 a.u. |
| Dipole Moment | 2.2103 Debeye |
| Point Group | C1 |
| Vibrational Frequency/cm-1 | Intensity | Vibration |
|---|---|---|
| 373 | 0 | 
|
| 396 | 0 | 
|
| 1737 | 4 | 
|
| 1757 | 4 | 
|
| 771 | 25 | 
|
The above table shows a bending and stretching frequency for the two alkenes as well as the major C-Cl stretch (highest intensity). The two bends are very low intensity, almost 0, and so mot much of an effect is seen, for the bends the alkene on the proton side has a higher frequency, ~20cm-1 higher, which is probably due to the bending modes being much lower in energy than stretching modes and so the effect of the C-Cl vibration is opposite to expected as another feature is taking precedence. The stretching modes have the opposite with the stretch close to the Cl being ~20cm-1 higher this is most likely due to the C-Cl stretch shown as the movement is much more towards the proton side of the structure distorting it more which would cause the frequency change. The intensity of the two stretches is almost the same.
Monosaccharide Chemistry
MM2 and MOPAC of A
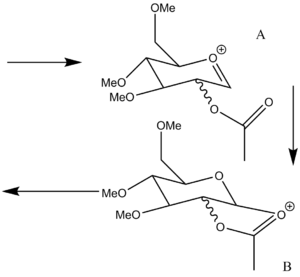
The glycosidation reaction, right, has two intermediates A and B which each have 2 different configurations with 2 different conformations the outcome of the reaction is determined by the intermediate geometries which have been explored below. The oxonium ion, A, has configurations based on the axial or equatorial position of the acyl group. Each of the configurations has 2 conformations based on whether the carbonyl on the acyl group is above or below the oxonium ion. Molecular mechanics, MM2, and MOPAC calculations were performed on the 4 structures with the data from these given below:
MM2:
Axial, below:
------------MM2 Minimization------------ Warning: Some parameters are guessed (Quality = 1). Iteration 540: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 2.8355 Bend: 13.6088 Stretch-Bend: 1.0211 Torsion: 2.3810 Non-1,4 VDW: 2.2933 1,4 VDW: 19.5541 Charge/Dipole: -39.7028 Dipole/Dipole: 10.2322 Total Energy: 12.2230 kcal/mol Calculation completed ------------------------------------
Axial, above:
------------MM2 Minimization------------ Warning: Some parameters are guessed (Quality = 1). Iteration 453: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 2.5261 Bend: 12.2235 Stretch-Bend: 0.8676 Torsion: 2.6367 Non-1,4 VDW: -2.1992 1,4 VDW: 19.6057 Charge/Dipole: -20.3743 Dipole/Dipole: 7.1808 Total Energy: 22.4670 kcal/mol Calculation completed ------------------------------------
Equatorial, above:
------------MM2 Minimization------------ Warning: Some parameters are guessed (Quality = 1). Iteration 402: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 2.7062 Bend: 12.6614 Stretch-Bend: 0.9782 Torsion: 2.9517 Non-1,4 VDW: -0.3639 1,4 VDW: 19.6849 Charge/Dipole: -30.9644 Dipole/Dipole: 10.9091 Total Energy: 18.5631 kcal/mol Calculation completed ------------------------------------
Equatorial, below:
------------MM2 Minimization------------ Warning: Some parameters are guessed (Quality = 1). Iteration 1039: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 2.3479 Bend: 10.5292 Stretch-Bend: 0.7595 Torsion: 1.4856 Non-1,4 VDW: -0.5764 1,4 VDW: 20.0076 Charge/Dipole: -25.1987 Dipole/Dipole: 5.6960 Total Energy: 15.0506 kcal/mol Calculation completed ------------------------------------
MOPAC
Axial, below:
------------ Mopac Interface ------------ Model: monosacc_mm2 Mopac Job: AUX RM1 CHARGE=1 EF GNORM=0.100 SHIFT=80 Finished @ RMS Gradient = 0.07692 (< 0.10000) Heat of Formation = -76.88217 Kcal/Mol -----------------------------------------
Axial, above:
------------ Mopac Interface ------------ Model: monosacc_mm2_conf Mopac Job: AUX RM1 CHARGE=1 EF GNORM=0.100 SHIFT=80 Finished @ RMS Gradient = 0.08943 (< 0.10000) Heat of Formation = -61.13441 Kcal/Mol -----------------------------------------
Equatorial, above:
------------ Mopac Interface ------------ Model: monosacc_mm2_2 Mopac Job: AUX RM1 CHARGE=1 EF GNORM=0.100 SHIFT=80 Finished @ RMS Gradient = 0.07639 (< 0.10000) Heat of Formation = -77.53737 Kcal/Mol -----------------------------------------
Equatorial, below:
------------ Mopac Interface ------------ Model: monosacc_mm2_2_conf Mopac Job: AUX RM1 CHARGE=1 EF GNORM=0.100 SHIFT=80 Finished @ RMS Gradient = 0.09521 (< 0.10000) Heat of Formation = -65.71069 Kcal/Mol -----------------------------------------
The data from the calculations above has been collated and is displayed in the following table with key geometries:
| Conformer | MM2 energy/ kcal/mol | MM2 O-C length/Å | MM2 O-C-O angle | MOPAC energy/ kcal/mol | MOPAC O-C length/Å | MOPAC O-C-O angle | |||
|---|---|---|---|---|---|---|---|---|---|
|
12.2230 | 2.50 | 83° | -76.88217 | 1.47 | 106° | |||
|
22.4670 | 4.20 | 121° | -61.13441 | 4.08 | 119° | |||
|
18.5631 | 2.53 | 104° | -77.53737 | 1.47 | 106° | |||
|
15.0506 | 2.90 | 158° | -65.71069 | 2.87 | 159° |
The O-C distance is between that of the carbonyl on the acyl group and the carbon double bonded to the oxonium ion, the angle measured was along the same distance and continuing to the oxygen. The data from the calculations suggests that the first conformation above has the lowest strain with the acyl group axial with the carbonyl groups close together. The other axial form is much higher in strain and has a long distance between the two carbonyl groups. If the acyl group is axial the conformation with the two carbonyl groups close together is most stable. This is also apparent in the MOPAC energy which is much more in favour of the close carbonyl groups; this can be justified by the acyl carbonyl donating into the ion reducing the strain and energy. The angle of this interaction is close to 90° which suggests an orbital effect and supports the acyl group donating.
For the equatorial group a similar effect is seen with the closer carbonyl groups being lower in energy, MOPAC, but the strain is in favour of the far acyl group. Again the angle is ~90° with the length of the interaction becoming close to bond length, 1.47Å, when the groups are close.
The two forms with the group close are much lower in energy to the other two conformations which implies they will be favoured. Of these two the energy of formation is very similar, a difference of less than 1 kcal/mol, but the strain is in favour of the axial acyl group. The distance and angle measured are the same in both systems suggesting a strong interaction between the two carbonyl groups.
MM2 and MOPAC of B
There are also 2 configurations of B with two conformers each, the calculations below were performed to find the geometry and energies of the different forms. The notation used is based on the position of the acyl group with the first term defining the position of the group and the second the position of the acyl ion bonding to the ring:
MM2:
Below, Below:
------------MM2 Minimization------------ Warning: Some parameters are guessed (Quality = 1). Iteration 316: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 2.0760 Bend: 14.1166 Stretch-Bend: 0.7521 Torsion: 9.6779 Non-1,4 VDW: -2.2920 1,4 VDW: 17.9017 Charge/Dipole: -9.5267 Dipole/Dipole: -2.0837 Total Energy: 30.6219 kcal/mol Calculation completed ------------------------------------
Below, Above:
------------MM2 Minimization------------ Warning: Some parameters are guessed (Quality = 1). Iteration 443: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 2.8094 Bend: 18.1009 Stretch-Bend: 0.8692 Torsion: 9.3802 Non-1,4 VDW: -2.2419 1,4 VDW: 19.0838 Charge/Dipole: 2.4684 Dipole/Dipole: -1.5852 Total Energy: 48.8847 kcal/mol Calculation completed ------------------------------------
Above, Below:
------------MM2 Minimization------------ Warning: Some parameters are guessed (Quality = 1). Iteration 671: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 2.6824 Bend: 19.8191 Stretch-Bend: 0.7843 Torsion: 8.6665 Non-1,4 VDW: -2.8757 1,4 VDW: 18.7670 Charge/Dipole: 2.0408 Dipole/Dipole: -1.5750 Total Energy: 48.3095 kcal/mol Calculation completed ------------------------------------
Above, Above:
------------MM2 Minimization------------ Warning: Some parameters are guessed (Quality = 1). Iteration 576: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 2.0264 Bend: 13.0410 Stretch-Bend: 0.7077 Torsion: 10.8720 Non-1,4 VDW: -4.2910 1,4 VDW: 18.5203 Charge/Dipole: -4.9102 Dipole/Dipole: -1.1299 Total Energy: 34.8363 kcal/mol Calculation completed ------------------------------------
MOPAC:
Below, Below:
------------ Mopac Interface ------------ Model: monosacc_mm2_bb Mopac Job: AUX RM1 CHARGE=1 EF GNORM=0.100 SHIFT=80 Finished @ RMS Gradient = 0.09636 (< 0.10000) Heat of Formation = -79.45281 Kcal/Mol -----------------------------------------
Below, Above:
------------ Mopac Interface ------------ Model: monosacc_mm2_ba Mopac Job: AUX RM1 CHARGE=1 EF GNORM=0.100 SHIFT=80 Finished @ RMS Gradient = 0.09200 (< 0.10000) Heat of Formation = -54.08797 Kcal/Mol -----------------------------------------
Above, Below:
------------ Mopac Interface ------------ Model: monosacc_mm2_ab Mopac Job: AUX RM1 CHARGE=1 EF GNORM=0.100 SHIFT=80 Finished @ RMS Gradient = 0.08254 (< 0.10000) Heat of Formation = -56.29131 Kcal/Mol -----------------------------------------
Above, Above:
------------ Mopac Interface ------------ Model: monosacc_mm2_aa Mopac Job: AUX RM1 CHARGE=1 EF GNORM=0.100 SHIFT=80 Finished @ RMS Gradient = 0.08035 (< 0.10000) Heat of Formation = -76.27828 Kcal/Mol -----------------------------------------
The data from the calculations above has been collated and is displayed in the following table with key geometries:
| Conformer | MM2 energy/ kcal/mol | MM2 O-C length/Å | MM2 O-C-O angle | MOPAC energy/ kcal/mol | MOPAC O-C length/Å | MOPAC O-C-O angle | |||
|---|---|---|---|---|---|---|---|---|---|
|
30.6219 | 1.41 | 119° | -79.45281 | 1.47 | 106° | |||
|
48.8847 | 1.41 | 123° | -54.08797 | 1.46 | 110° | |||
|
48.3095 | 1.41 | 124° | -56.29131 | 1.45 | 111° | |||
|
34.8363 | 1.41 | 111° | -76.27828 | 1.45 | 100° |
The O-C distance is the bond length between the acyl ion and the carbon it is singly bonded to, the angle is the O-C-O bond angle between the acyl group and the single bonded carbon to oxygen. As the length given is the bond length the MM2 calculation gives the bond length as the same which is due to the calculation type keeping the length standard. The analysis is very similar to the system above, A, with two conformers being higher in energy. The two higher strain systems also have lower energies of formation which suggests these are very disfavoured comparatively this is due to the bond angle being larger by about 5° making the bonding slightly less effective.
The other two conformers are the same as the two most stable A conformers with very similar geometries and energies, the difference being minor, this implies that in the system A a bond is formed which was the conclusion from the data. The difference between the two proposed structures is a small electronic change to move the cation however this is only formally whereas it is most likely there is no difference between the species.
Week 2
Spectroscopy of Taxol intermediate
Optimisation of taxol intermediate
| The structure shown is an intermediate in the formation of taxol, further along the synthetic path than the intermediate studied above, only one isomer has been used although another is possible with similar differences to those above. The use of this molecule is to practice calculating NMR spectra. To start with the molecule is minimized by molecular mechanics calculations which gives the data below: |
|
------------MM2 Minimization------------ Warning: Some parameters are guessed (Quality = 1). Iteration 304: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 5.4335 Bend: 20.8065 Stretch-Bend: 0.8275 Torsion: 21.8136 Non-1,4 VDW: 1.9593 1,4 VDW: 16.6333 Dipole/Dipole: -2.2659 Total Energy: 65.2078 kcal/mol Calculation completed ------------------------------------
Taking this optimised structure the system was further optimised to the conditions that NMR will be calculated. The system was optimised using DFT B3LYP calculations with 6-31G(d,p) as the basis set. The NMR calculation will be performed using simulated solvent and so the optimisation was also performed using this, the solvent model used was CPCM with chloroform as solvent. The calculation gave the following when published [2] with the summary of the calculation given below:
| Calculation type | FOPT |
| Calculation Method | RB3YP |
| Basis Set | 6-31G(d,p) |
| E(RB3LYP) | -1651.80160881 a.u. |
| RMS Gradient Norm | 0.00001012 a.u. |
| Dipole Moment | 4.1259 Debeye |
| Point Group | C1 |
NMR of optimised structre
The optimised structure was then used to calculate the NMR of the molecule using the rmpw1pw91 calculation method with the same basis set as above, 6-31G(d,p), and the same solvent system, CPCM, solvent=chloroform, the results of the calculation are given here [3].
| Calculation type | SP |
| Calculation Method | RMPW1PW91 |
| Basis Set | 6-31G(d,p) |
| E(RB3LYP) | -1651.64063734 a.u. |
| RMS Gradient Norm | 0.00000000 a.u. |
| Dipole Moment | 4.2030 Debeye |
| Point Group | C1 |
The calculated NMR spectrum is given below, using TMS as zero:
The NMR from literature [4] is also given as data which is compared to the calculated data in the table below:
| Experimental Data/ppm | Calculated Data/ppm |
| 218.8 | 217.7 |
| 144.6 | 146.6 |
| 125.3 | 125.5 |
| 72.9 | 88.7 |
| 56.2 | 60.1 |
| 52.5 | 57.2 |
| 48.5 | 52.0 |
| 46.8 | 51.3 |
| 45.8 | 47.6 |
| 39.8 | 43.6 |
| 38.8 | 41.6 |
| 35.9 | 41.5 |
| 32.7 | 35.9 |
| 28.8 | 31.3 |
| 28.3 | 28.7 |
| 26.9 | 28.5 |
| 25.7 | 27.4 |
| 23.9 | 26.3 |
| 21.0 | 24.5 |
| 18.7 | 20.3 |
The data for the experimental and calculated data are very similar but there are some significant differences. Most of the peaks correlate reasonably with only minor discrepancies in ppm which could be due to calculation errors as the model is not perfect the error could also be due to impurities in the sample or other error. A major difference is around 72.9 ppm a peak is given in the experimental data however the corresponding peak is at 88.7 ppm which is hugely different and suggests that the molecule orientation may be wrong or the peak is very small on the experimental NMR and so was neglected however no other calculated peak corresponds well with the peak at 72.9 ppm. The peak at 60.1 ppm is also not seen in the experimental data and the other peaks correlate better if this peak is not used, again this may be due to the relaxation time of the carbon being too long to give a noticeable signal. The lower ppm peaks correlate well with the peak in the next row, experimental to calculation, which suggests that the carbons at 88 and 60 ppm are wrong in the calculation although due to time this cannot be re-done.
Literature Molecule
Proposed literature structure optimisation and NMR
| A molecule was found in recent literature [5] which has the possibility to be one of 4 isomers. The paper suggests that only one isomer is formed, shown right, this will be tested using NMR calculations to confirm whether the structure is correct. NMR will give small differences between the isomers due to minor changes is environment which can be used to confirm structure. Also IR spectroscopy could be used as the vibrations for the isomers will be slightly different for each form. To decide on which form was created the molecule was optimised using molecular mechanics, MM2, which lead to the data below: |
|
------------MM2 Minimization------------ Separating coincident atoms: Lp(50)-Lp(51) Pi System: 23 22 5 6 21 9 24 25 Pi System: 18 17 8 2 16 1 19 20 Pi System: 13 12 11 10 14 15 Warning: Some parameters are guessed (Quality = 1). Iteration 941: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 2.4489 Bend: 12.0909 Stretch-Bend: 0.1052 Torsion: -17.7670 Non-1,4 VDW: 0.3694 1,4 VDW: 26.1761 Dipole/Dipole: -0.4993 Total Energy: 22.9241 kcal/mol Calculation completed ------------------------------------
Further optimisation for NMR calculations was performed using Gaussian with the method similar to that used above. RB3YP/6-31G(d,p) method and basis set was used with solvent model CPCM and chloroform as solvent, the optimisation gave the following when published [4]. A summary of the calculation is given below:
| Calculation type | FOPT |
| Calculation Method | RB3YP |
| Basis Set | 6-31G(d,p) |
| E(RB3LYP) | -1116.38190321 a.u. |
| RMS Gradient Norm | 0.00000617 a.u. |
| Dipole Moment | 4.7952 Debeye |
| Point Group | C1 |
NMR calculations were performed using the MPW1PW91 method, 6-31G basis set and CPCM solvent model(chloroform) the published data is given here[5]. A summary of this data is below:
| Calculation type | SP |
| Calculation Method | RMPW1PW91 |
| Basis Set | 6-31G(d,p) |
| E(RB3LYP) | -1116.1259020 a.u. |
| RMS Gradient Norm | 0.00000000 a.u. |
| Dipole Moment | 4.8482 Debeye |
| Point Group | C1 |
The calculated NMR spectrum of the proposed structure is given, when TMS is used as zero in CDCl3:
The literature NMR:
A summary of the calculated NMR and the literature NMR are given in the following table:
| Experimental Data | Calculated Data |
| 201.1 | 198.2 |
| 156.8 | 154.7 |
| 136.9 | 135.5 |
| 135.8 | 133.3 |
| 133.9 | 132.9 |
| 131.9 | 131.9 |
| 128.4 | 131.1 |
| 128.3 | 129.8 |
| 128.1 | 128.1 |
| 127.7 | 127.3 |
| 127.4 | 127.1 |
| 126.9 | 126.1 |
| 125.8 | 125.9, 125.8, 125.6, 124.0 |
| 120.6 | 122.9, 122.9, 117.0 |
| 110.2 | 108.2 |
| 54.7 | 56.0 |
| 52.6 | 54.0 |
| 49.8 | 54.0 |
| 37.8 | 41.6 |
The data shows a strong correlation with all the points being within a small ppm range when comparing experimental to calculated data. The issue with the data however is that the peaks from 125.9 to 117.0 ppm in the calculated system are 7 separate signals however only two signals are reported in the experimental data this could be due to overlapping signals as they are very close together, this can be seen in the data as some signals are much stronger than others which could be due to overlap or relaxation times. Overall the data shows quite strongly that the proposed molecule is correct however another isomer of the species will be looked at for completion.
Isomer of literature structure optimisation and NMR
| An isomer of the system above was optimised in the same manner starting with molecular mechanics, MM2, calculations the results are given below: |
|
------------MM2 Minimization------------ Pi System: 23 22 5 6 21 9 24 25 Pi System: 18 17 8 2 16 1 19 20 Pi System: 13 12 11 10 14 15 Warning: Some parameters are guessed (Quality = 1). Iteration 759: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 2.6737 Bend: 12.8507 Stretch-Bend: 0.1380 Torsion: -15.8603 Non-1,4 VDW: 0.4464 1,4 VDW: 26.3650 Dipole/Dipole: 0.4396 Total Energy: 27.0531 kcal/mol Calculation completed ------------------------------------
The system was then further optimised using the RB3LYP method with 6-31G basis set, the chloroform solvent was modelled using CPCM. The published data is given here[6]. A summary of the calculation is given below:
| Calculation type | FOPT |
| Calculation Method | RB3YP |
| Basis Set | 6-31G(d,p) |
| E(RB3LYP) | -1116.37085713 a.u. |
| RMS Gradient Norm | 0.00000765 a.u. |
| Dipole Moment | 1.9420 Debeye |
| Point Group | C1 |
The NMR spectrum was then calculated for the isomer using the RMPW1PW91 method with 6-31G(d,p) basis set and same solvent model as above the results were published here [7]. A summary of the calculation is below:
| Calculation type | SP |
| Calculation Method | RMPW1PW91 |
| Basis Set | 6-31G(d,p) |
| E(RB3LYP) | -1116.11497652 a.u. |
| RMS Gradient Norm | 0.00000000 a.u. |
| Dipole Moment | 1.9725 Debeye |
| Point Group | C1 |
The calculated spectrum is shown here, using TMS as zero:
| Experimental Data | Calculated Data |
| 201.1 | 195.7 |
| 156.8 | 155.6 |
| 136.9 | 134.5 |
| 135.8 | 133.9 |
| 133.9 | 132.7 |
| 131.9 | 132.2 |
| 128.4 | 130.5 |
| 128.3 | 127.8 |
| 128.1 | 127.7 |
| 127.7 | 127.1 |
| 127.4 | 126.4 |
| 126.9 | 126.0 |
| 125.8 | 125.7, 125.6, 124.8, 123.7 |
| 120.6 | 123.0, 122.6, 116.4 |
| 110.2 | 108.1 |
| 54.7 | 55.6 |
| 52.6 | 54.0 |
| 49.8 | 53.7 |
| 37.8 | 39.6 |
The comparison is to the above experimental to see if the structure is correct. Again this is very similar as expected and the analysis above applies here as well with the same issue of multiple signals and minor differences. The calculated system for the isomer does however have slight differences from the other calculated system which make it further from the experimental spectrum overall suggests that the isomer is not the correct species.
Conclusion
The NMR data doesn't strongly suggest the correct structure either way due to calculation inadequacies however it is assumed that the correct form was given in the paper as this is the form produced by the mechanism, proposed in the paper[5], which is shown below. The isomer could also be determined using infrared spectroscopy as there will be slightly different vibrations due to the different geometries:
The preference for the given stereochemistry will be due to the addition of the dione to the activated species, I. The mechanism could be explored by calculating the intermediates with differing stereochemistry and determining the most stable species and so which species is preferred when the reaction continues.
References and citations
- ↑ W. F. Maier , P. V. R. Schleyer, J. Am. Chem. Soc., 1981, 103, 1900 DOI:10.1021/ja00398a003
- ↑ D. K. Johnson, B. P. Mundy, Tetrahedron Letters, 1989, 30 (48), 6633 DOI:10.1016/S0040-4039(00)70637-X
- ↑ 3.0 3.1 Gaussian 03, Revision E.01, M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez, and J. A. Pople, Gaussian, Inc., Wallingford CT, 2004.
- ↑ L. A. Paquette , N. A. Pegg , D. Toops , G. D. Maynard , R. D. Rogers, J. Am. Chem. Soc., 1990, 112, 283 DOI:10.1021/ja00157a043
- ↑ 5.0 5.1 R. R. Paul, K. S. Lakshmi, E. Suresh, V. Nair, Tetrahedron Letters, 2013, 54 (16), 2046 DOI:10.1016/j.tetlet.2013.01.100