Rep:Mod:JF1234
Computational Lab: Introduction to Molecular Modelling 2
Haber-Bosch Process
I am investigating the Haber-Bosch process by using computations to optimise the structures of ammonia, hydrogen and nitrogen. This also results in an estimate of their energies which can be used to calculate the energy change of the reaction.
NH3
Molecule: NH3
Calcuation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy (au): -56.55776873
RMS gradient (au): 0.00000485
Point group: C3v
N-H bond length (Å): 1.01798
H-N-H bond angle (°): 105.741
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
NH3 |
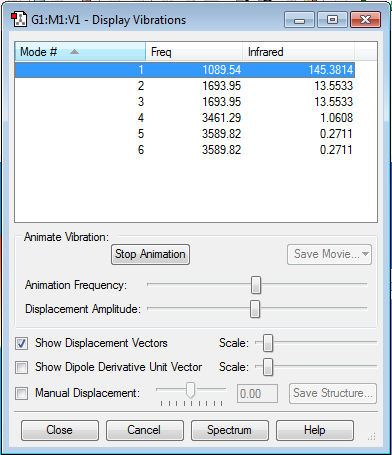
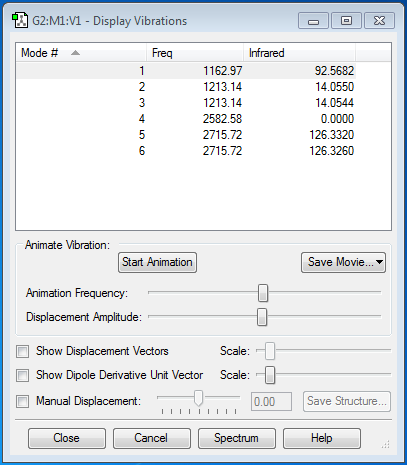
According to the 3N-6 rule, 6 vibrational modes are expected, and 6 modes are present. There are 2 sets of 2 modes which are degenerate, 2&3 and 5&6. Modes 1-3 are bending modes and 4-6 are stretching. Mode 4 is highly symmetric, having a C3 axis, 3 C2 axes and 3 σv. Mode 1 is the 'umbrella' mode. I would expect to see 2 bands in an experimental spectrum of gaseous ammonia because vibrational modes 4-6 are of a low intensity so are likely to be lost due to noise and modes 2&3 are degenerate so will result in a single band.
N Charge: -1.125 e
H Charge: 0.375 e
This tallies with expectation - nitrogen is more electronegative than hydrogen so will attract more electrons, causing a negative charge to collect.
N2
Molecule: N2
Calcuation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy (au): -109.52412868
RMS gradient (au): 0.00000060
Point group: D∞h
N-N bond length (Å): 1.10550
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
N2 |
According to the 3N-5 rule, only one vibrational mode is expected. No bands would be seen in a spectrum because the intensity of the mode is 0.
The charge on each atom is 0, this is expected as there is no electronegativity difference so the charge will be distributed evenly.
H2
Molecule: H2
Calcuation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy (au): -1.17853936
RMS gradient (au): 0.00000017
Point group: D∞h
H-H bond length (Å): 0.74279
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
H2 |
According to the 3N-5 rule, only one vibrational mode is expected. No bands would be seen in a spectrum because the intensity of the mode is 0.
The charge on each atom is 0, this is expected as there is no electronegativity difference so the charge will be distributed evenly.
Reaction Energies for Haber-Bosch Process
E(NH3)= -56.55776873 au
2*E(NH3)= -113.11553746 au
E(N2)= -109.52412868 au
E(H2)= -1.17853936 au
3*E(H2)= -3.53561808 au
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05522798 au
ΔE= -145.00 kJ/mol
The product is more stable than the reactants.
HCl
Results of Optimisation
Molecule: HCl
Calcuation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy (au): -460.80077875
RMS gradient (au): 0.00005211
Point group: C∞h
H-Cl bond length (Å): 1.28599
Item Value Threshold Converged? Maximum Force 0.000090 0.000450 YES RMS Force 0.000090 0.000300 YES Maximum Displacement 0.000139 0.001800 YES RMS Displacement 0.000197 0.001200 YES
HCl |
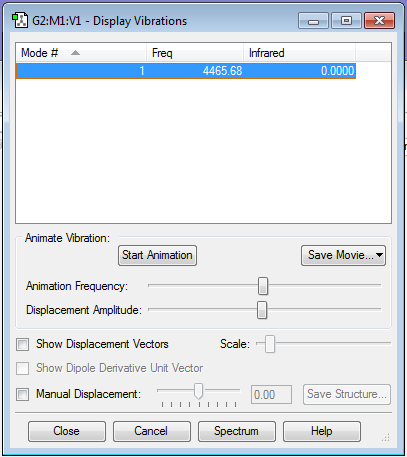
The molecule has only 1 vibration mode which is expected under the 3N-5 rule. This will produce a band in the spectrum of HCl.
Chlorine has a charge of -0.284 e, meaning hydrogen has a charge of 0.284 e. This is expected as chlorine is more electronegative than hydrogen.
Molecular Orbitals
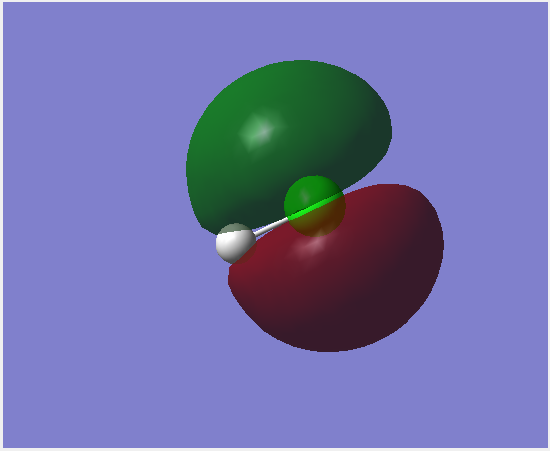
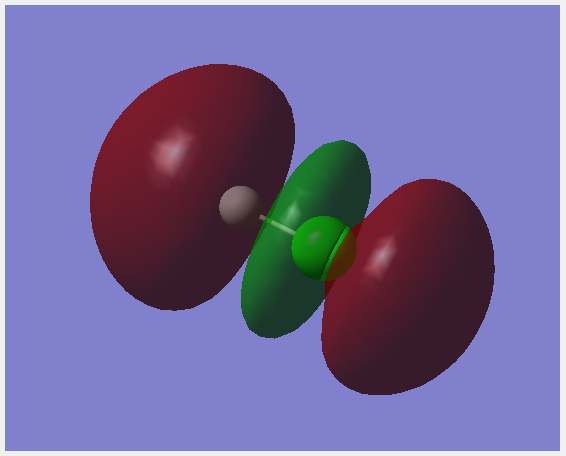
This molecular orbital is made up of the 1s orbital on chlorine. It is occupied and non-bonding. It is very low in energy.
The 3s orbitals on chlorine forms this bonding orbital with a small interaction from 1s on hydrogen. This orbital is occupied and contributes to bonding. It is relatively low in energy.
The 3p orbital on chlorine directed along the bond interacts with the 1s orbital on hydrogen together to form this σ bonding orbital. It is occupied and is close to the energy of the HOMO.
This orbital is formed by a 3p orbital on chlorine, it is a non-bonding orbital. This orbital is the HOMO. It is occupied.
This is the anti-bonding combination of a 3p orbital pon chlorine and the 1s on hydrogen forming a σ anti-bonding orbital. It is the LUMO. It is unoccupied.
BH3
Molecule: NH3
Calcuation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy (au): -26.61532364
RMS gradient (au): 0.00000211
Point group: D3h
B-H bond length (Å): 1.19232
H-B-H bond angle (°): 120.000
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000003 0.000300 YES Maximum Displacement 0.000017 0.001800 YES RMS Displacement 0.000011 0.001200 YES
BH3 |
Borane has 6 vibrational modes which follows the 3N-6 rule. Much like ammonia, there are 2 sets of 2 degenerate modes. I would expect to see 3 bands in the spectrum because there are 2 degenerate peaks and 1 of very low intensity.
The boron atom has a charge of 0.095 e on it and each hydrogen has a charge of -0.032 e on it. This is expected because hydrogen is slightly more electronegative than boron.