Rep:Mod:JB1995
Introduction
Gaussian, introduced in 1970, is a computer software which allows the user to model molecules in order to explore how they react with one another. This task was an exercise in characterising and locating the transition structures focussing solely on the molecules reacting pericyclically.
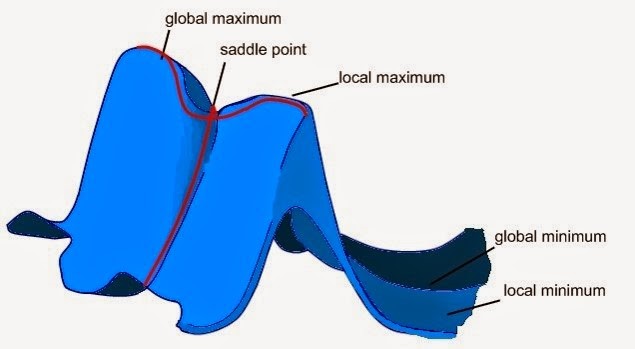
Figure 1: 2D potential energy surface [1]
As shown from the figure above, the bottom of the valley on a 2D potential energy surface is known as a minimum, these can be; local minimum, global minimum, or a saddle point. The dimension of the potential energy surface is directly related to the number of degrees of freedom in the system, in this case the number of normal modes, therefore the value of the energy is a function of these two normal modes. Upon optimisation of a molecule, a stationary point is located, such stationary point is where the first derivative of the energy is equal to zero, therefore locating either a minima or a saddle point, meaning the forces are zero. Such optimisations in geometry are used in order to locate the minimum energy structure, therefore resulting in a molecule that is closest to the ‘actual’ initial geometry. A transition state is the maximum along the minimum energy of the reaction path, which is located between the reactants and products, the minimum energy points, this is also known as a first order saddle point.
Because the first derivative of a saddle point and a minima point are both zero, a second derivative needs to be calculated in order to differentiate between them. If the second derivative is negative, the energy must decrease in the direction of the reaction path, and therefore is a saddle point, the opposite is said for a minima, in which the energy increases in all directions.
(It is important to note that for an N-dimensional PES, there are N orthogonal coordinates in which the second derivative can be taken. How many of these need to be maxima to be a transition state? Tam10 (talk) 14:16, 22 June 2017 (BST))
Computational Methods
In order to approximate the molecular orbitals, a linear combination of Gaussian functions are used. In this task there were two methods used in order to evaluate these integrals;
- PM6, Semi empirical- Many approximations and parameters are obtained from empirical data in order for inclusion of electron correlation is used within the Hartree-Fock analysis method. This method provides a much faster but less precise evaluation. This is used to find an initial geometry. [2]
- B3LYP, 631G(d), DFT- Density Function Theory uses the electron density of a molecule to determine the properties of the molecule. This is much more expensive and longer than the Semi-Empirical method. [3]
Exercise 1: Reaction of Butadiene with Ethylene
This reaction is a [4+2] cycloaddition reaction between a diene, in the s-cis conformation and a dienopile, a substituted alkene. The transition state is a 6π electron system in which 2 new sigma bonds are formed. These reactions are controlled by kinetics and orbital symmetry. [4]
Figure 2: Exercise 1 Mechanism
In Exercise 1 the reaction between butadiene and ethylene is computed and analysed with the pm6 semi empirical method.
Molecular Orbital Analysis
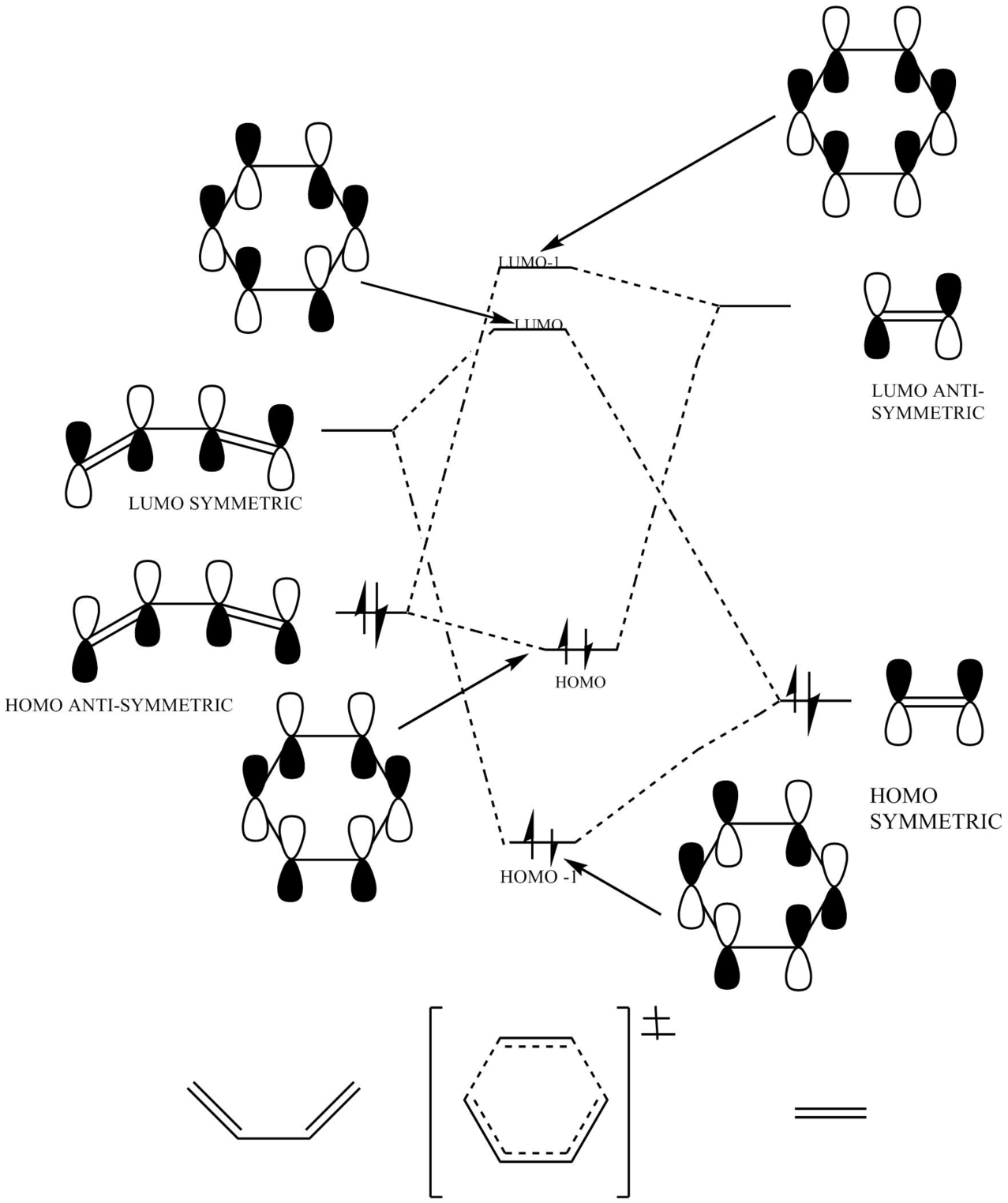
A molecular orbital diagram was constructed using the frontier molecular orbitals present in the diene and dienophile.
Figure 3: Exercise 1 Molecular Orbital Diagram
(Your MO diagram is a bit misleading. Don't use full bonds for the formed MOs as it looks like it could be planar from this angle. You have a mistake in the BD HOMO Tam10 (talk) 14:16, 22 June 2017 (BST))
From Figure 3 it is evident that molecular orbitals can only react if they are the same symmetric, meaning that antisymmetric-symmetric interactions are forbidden and do not take place. This is due to the nature of the orbital overlap integral equalling zero for 'non-same' interactions.
| Molecule | Butadiene | Ethylene |
|---|---|---|
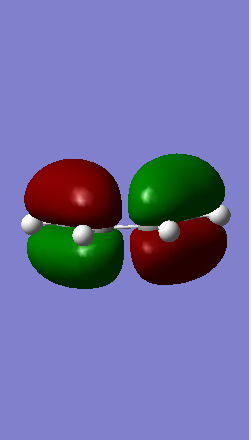 Antisymmetric Antisymmetric
|
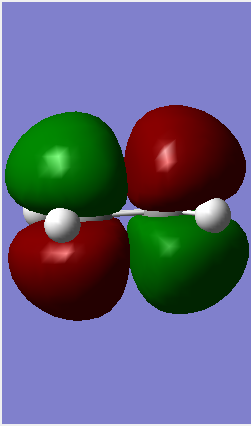 Symmetric Symmetric
| |
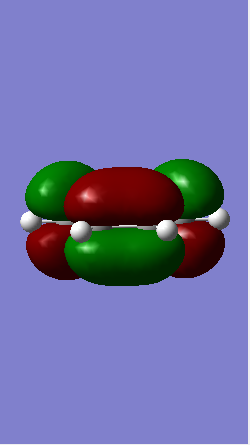 Antisymmetric Antisymmetric
|
 Symmetric Symmetric
|
| Transition State Molecular Orbitals | |||
|---|---|---|---|
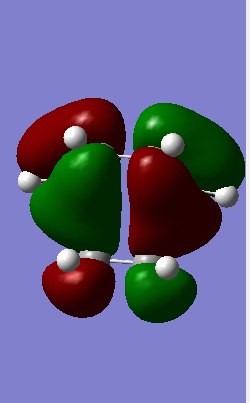 HOMO-1 Antisymmetric HOMO-1 Antisymmetric
|
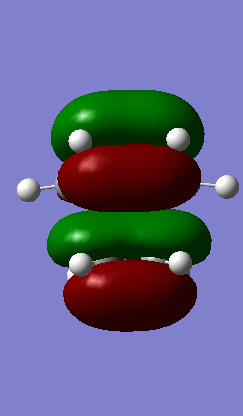 HOMO Symmetric HOMO Symmetric
|
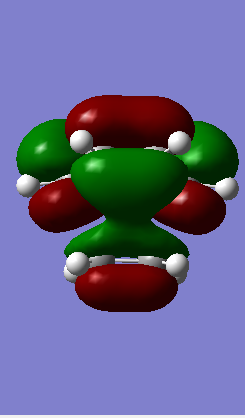 LUMO Symmetric LUMO Symmetric
|
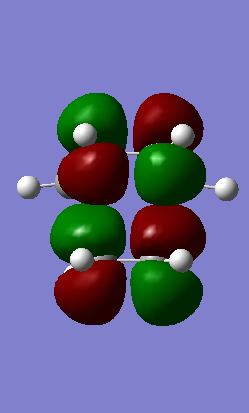 LUMO+1 Antisymmetric LUMO+1 Antisymmetric
|
Table 1: Molecular Orbital Representation from Gaussview
From Table 1 it is clear that only symmetric-symmetric or antisymmetric-antisymmetric interactions take place, with the transition state maintaining the same symmetry label as that for the two reacting molecular orbitals.
(What about the overlap integrals for differing symmetries? Tam10 (talk) 14:16, 22 June 2017 (BST))
Bond Distances
A bond distance analysis is compiled below, documenting the change in bond distances from reactants to the transition state.
Figure 5: Cyclohexene Bond Distances
| Internuclear Distances between Carbons/Å | C1-C2 | C2-C3 | C3-C4 | C4-C5 | C5-C6 | C6-C1 |
|---|---|---|---|---|---|---|
| Reactants | 1.47 | 1.34 | - | 1.33 | - | 1.34 |
| Transition State | 1.41 | 1.38 | 2.11 | 1.38 | 2.11 | 1.38 |
| Product | 1.34 | 1.50 | 1.54 | 1.54 | 1.54 | 1.50 |
Table 2: Table showing relevant bond distances
From Table 2 the typical bond length of two sp2 hybridised carbons doubly bonded is around 1.34Å and for two sp3 hybridised singly bonded to one another is around 1.53Å.[5] As a transition state approaches the double bond lengths become much shorter almost to the similar length to that of a singly bonded Carbon-Carbon. The sigma bonds that are produced in this reaction still remain longer than that of the a normal sp3 carbon- carbon in the transition state.
Vibrational Analysis and IRC
The obtained transition state underwent an intrinsic reaction coordinate calculation, this along with the vibration obtained from the imaginary frequency can be seen below.
| Vibrational Analysis | IRC |
|---|---|
 -948.98cm−1 -948.98cm−1
|
 Synchronous Synchronous
|
Table 3: Vibrations and IRC
Because bond formation occurs at the same time on each side of the reactant, this diels alder reaction can be thought of as synchronous.
Calculation Files
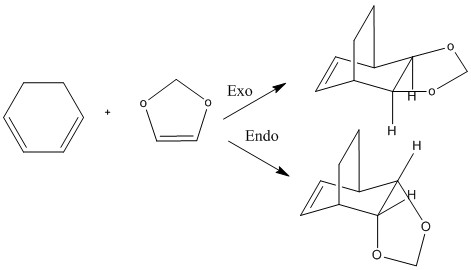
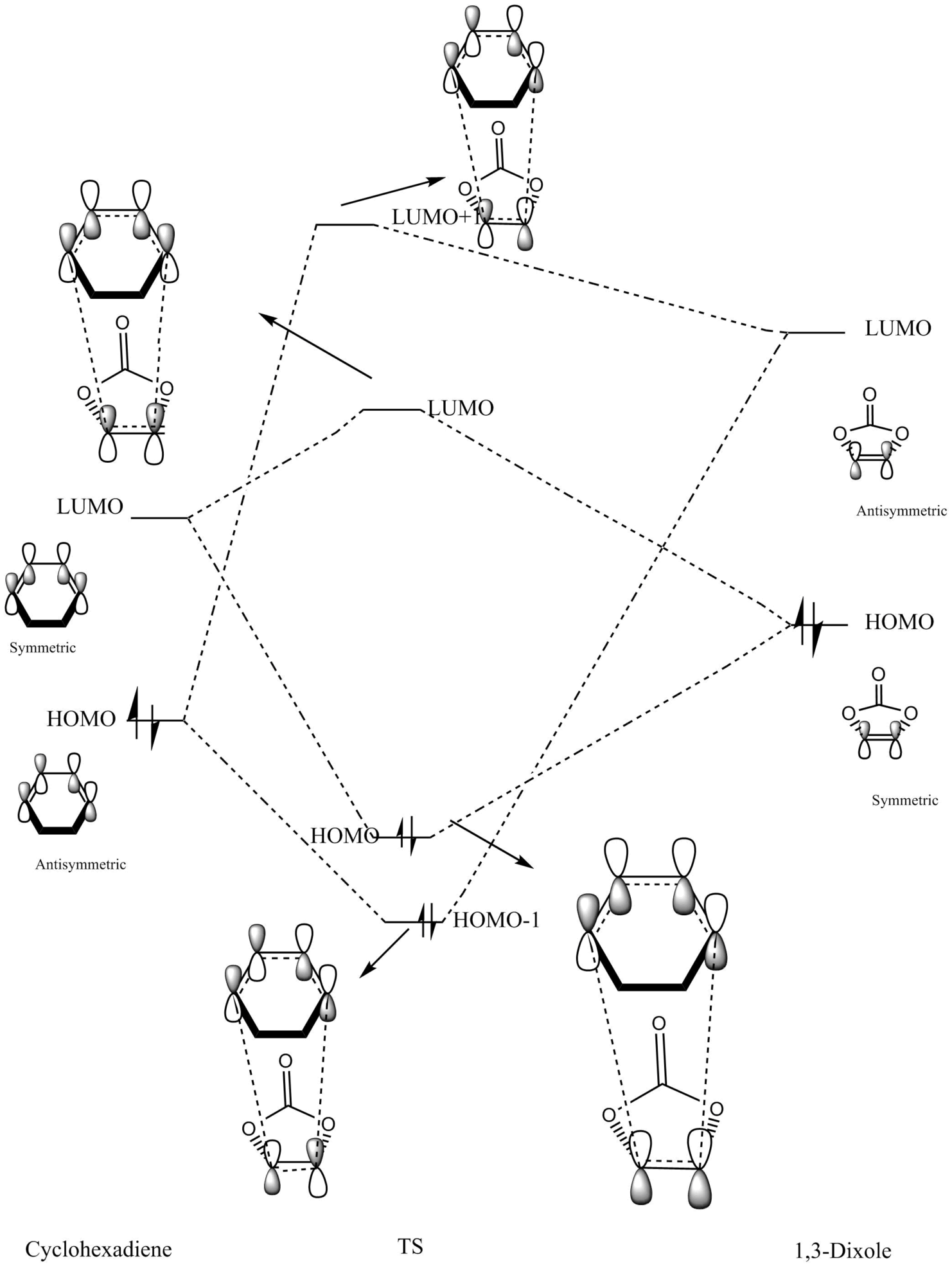
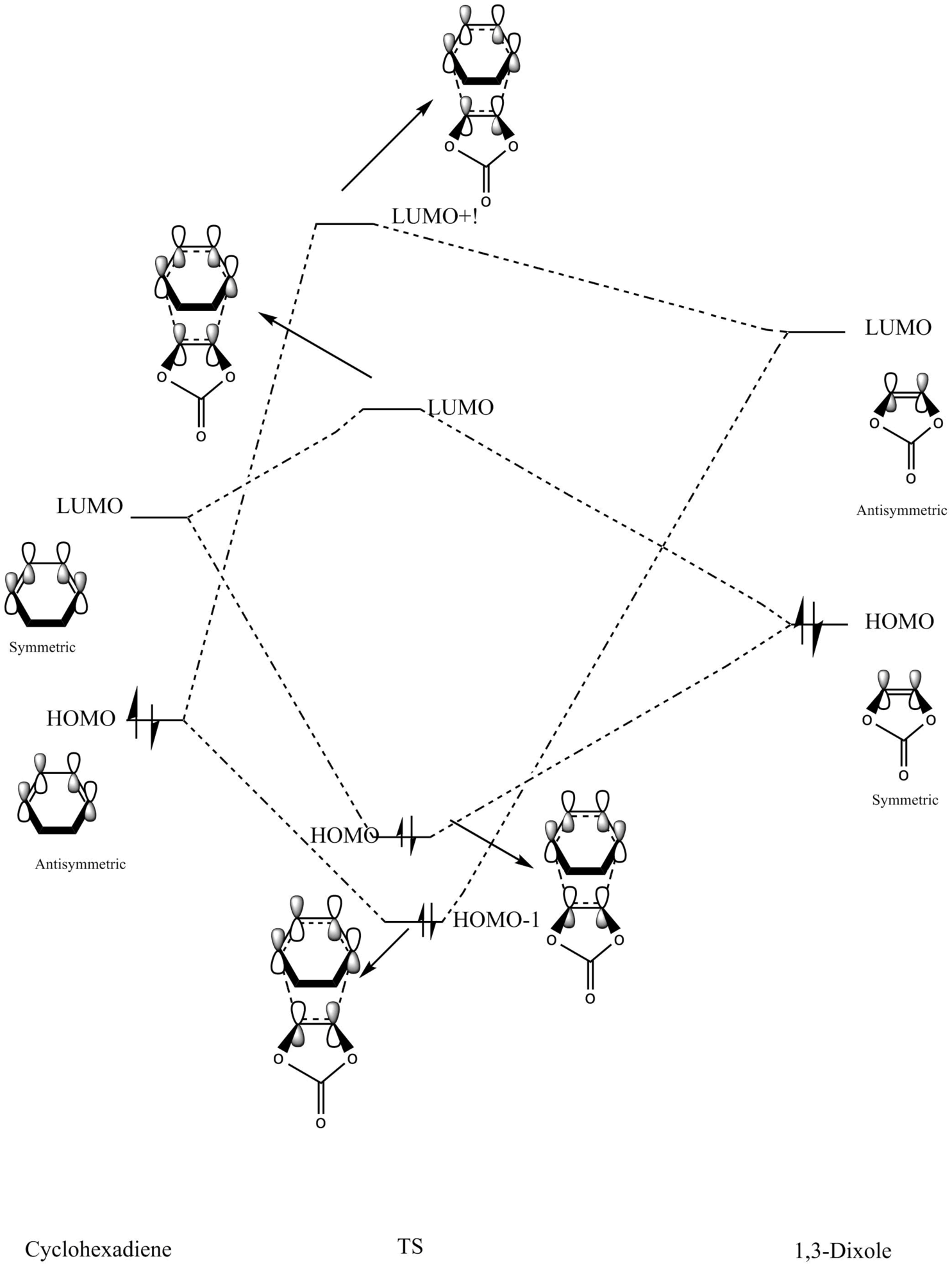
Exercise 2: Reaction of 1,3-dixole and cyclohexadiene
Figure 7: Mechansim for reaction between 1,3-dixole and cyclohexadiene Reference
Cyclohexadine and 1,3-dioxole react to form two products, an exo and an endo adduct. This reaction, again, is a [4+2] Diels-Alder cycloaddition. Because 1,3-dioxole contains two oxygen atoms in place of carbon atoms, this dienophile can produce better orbital overlap. This calculation was performed under the density function theory method with a basis set B3LYP/6-31(d).
Molecular Orbital Analysis
| Endo Transition State Molecular Orbital Diagram | Exo Transition State Molecular Orbital Diagram |
|---|---|
|
|
(These images are a bit too large Tam10 (talk) 14:16, 22 June 2017 (BST))
Figure 8: Molecular Orbital Analysis of Endo and Exo Transition States
| Column 1, Row 1 | ENDO | EXO |
|---|---|---|
| LUMO +1 | 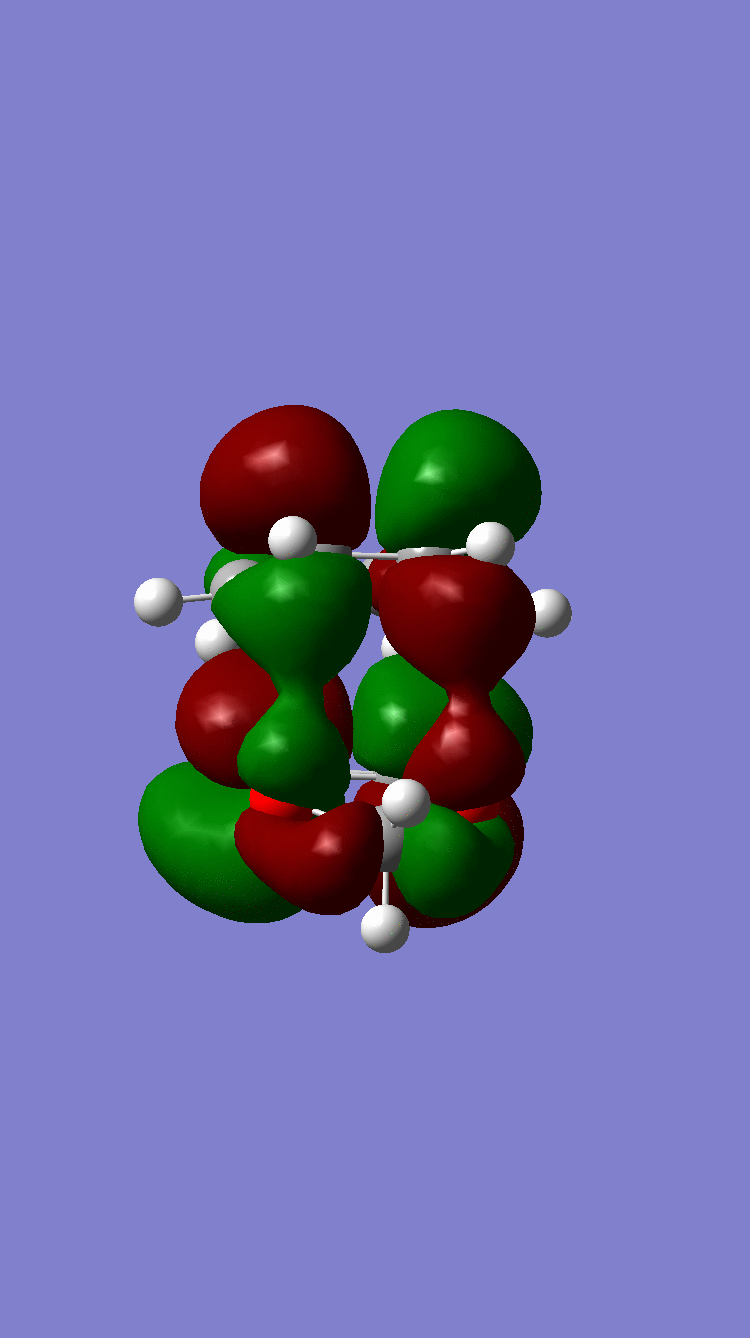 Antisymmetric Antisymmetric
|
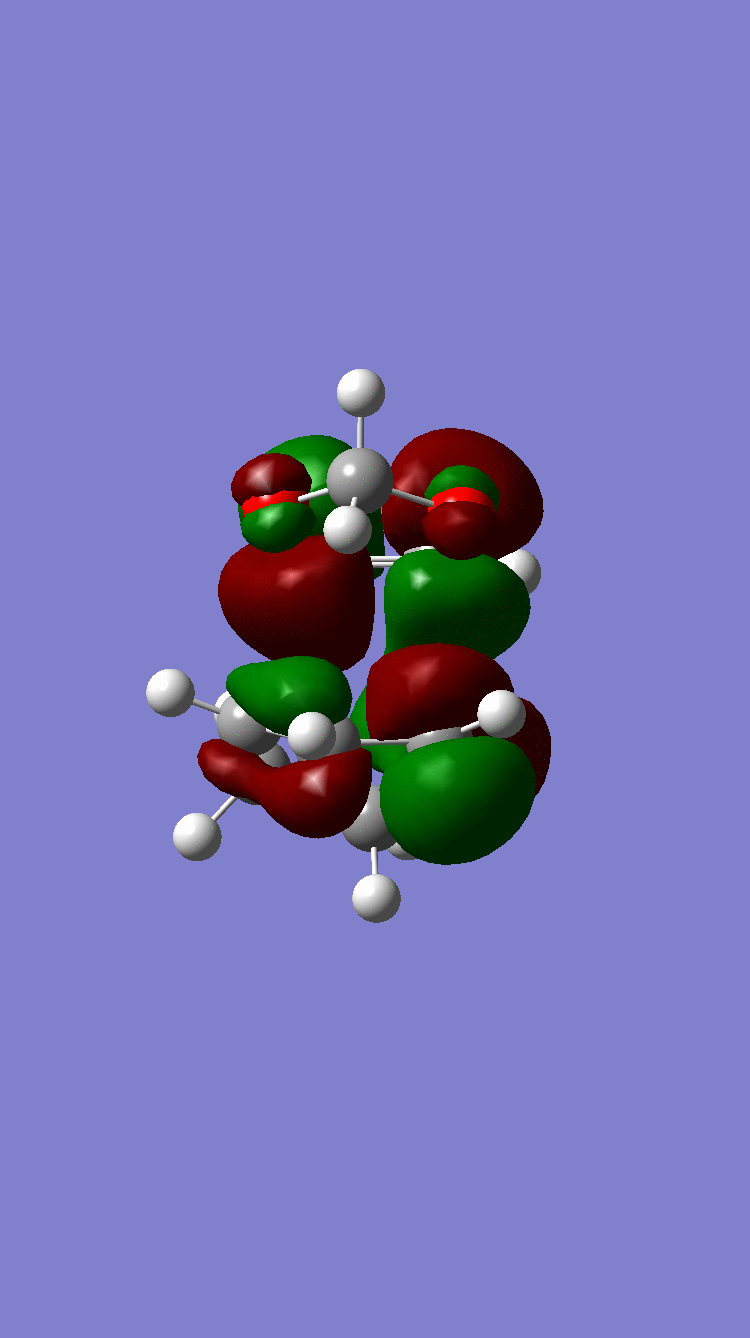 Antisymmetric Antisymmetric
|
| LUMO | 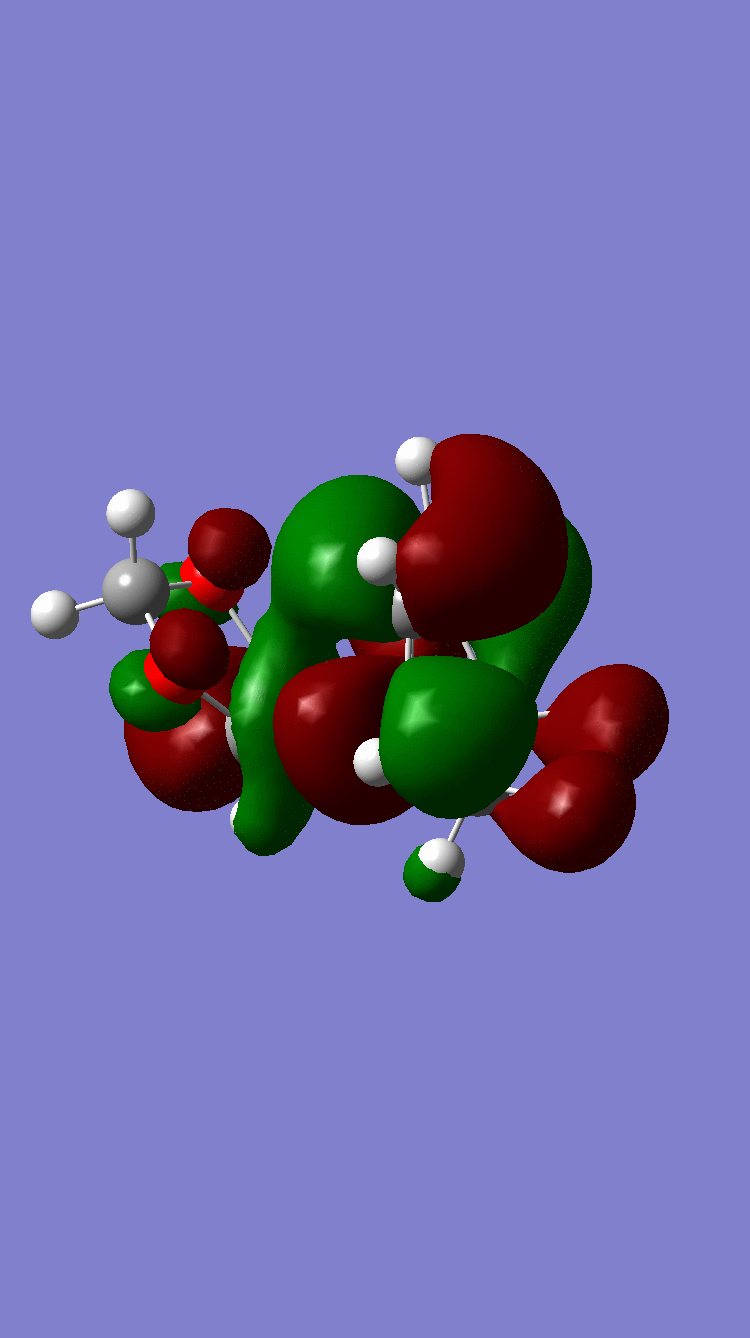 Symmetric Symmetric
|
 Symmetric Symmetric
|
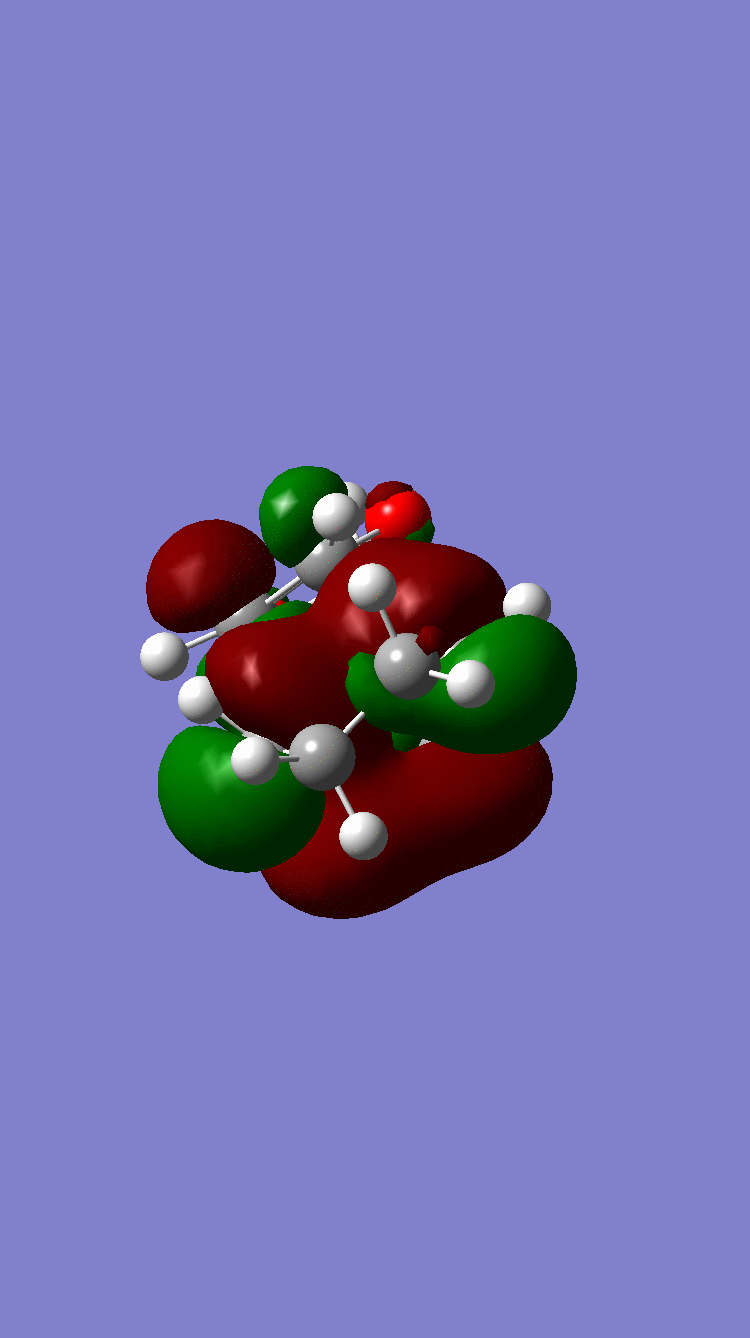
| HOMO | 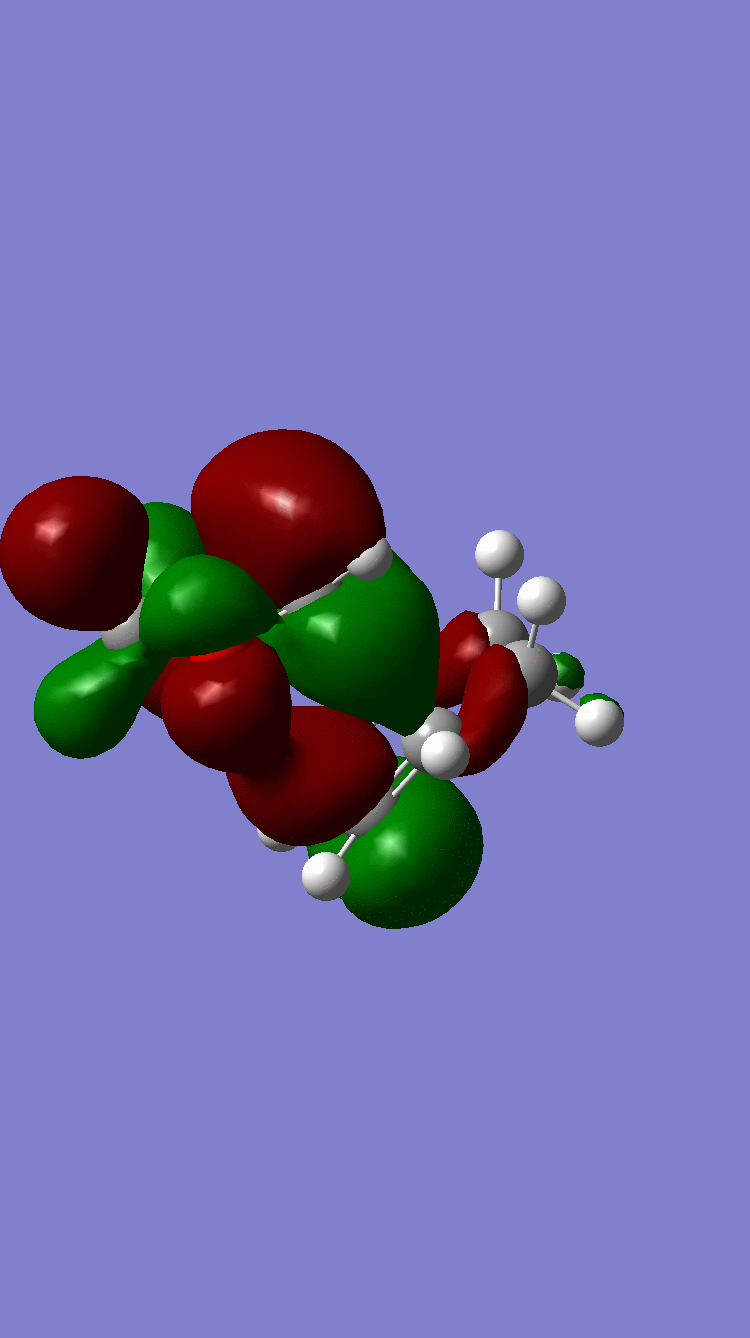 Symmetric Symmetric
|
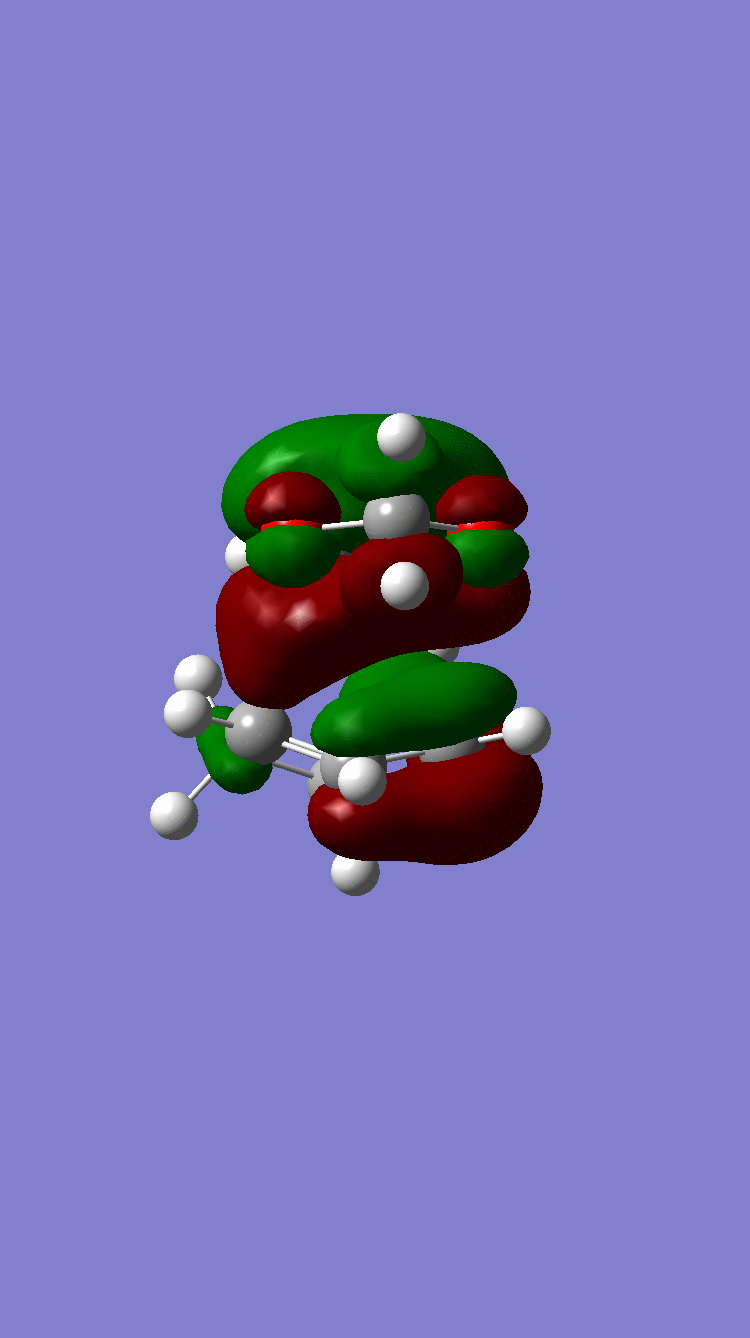 Symmetric Symmetric
|
| HOMO-1 | 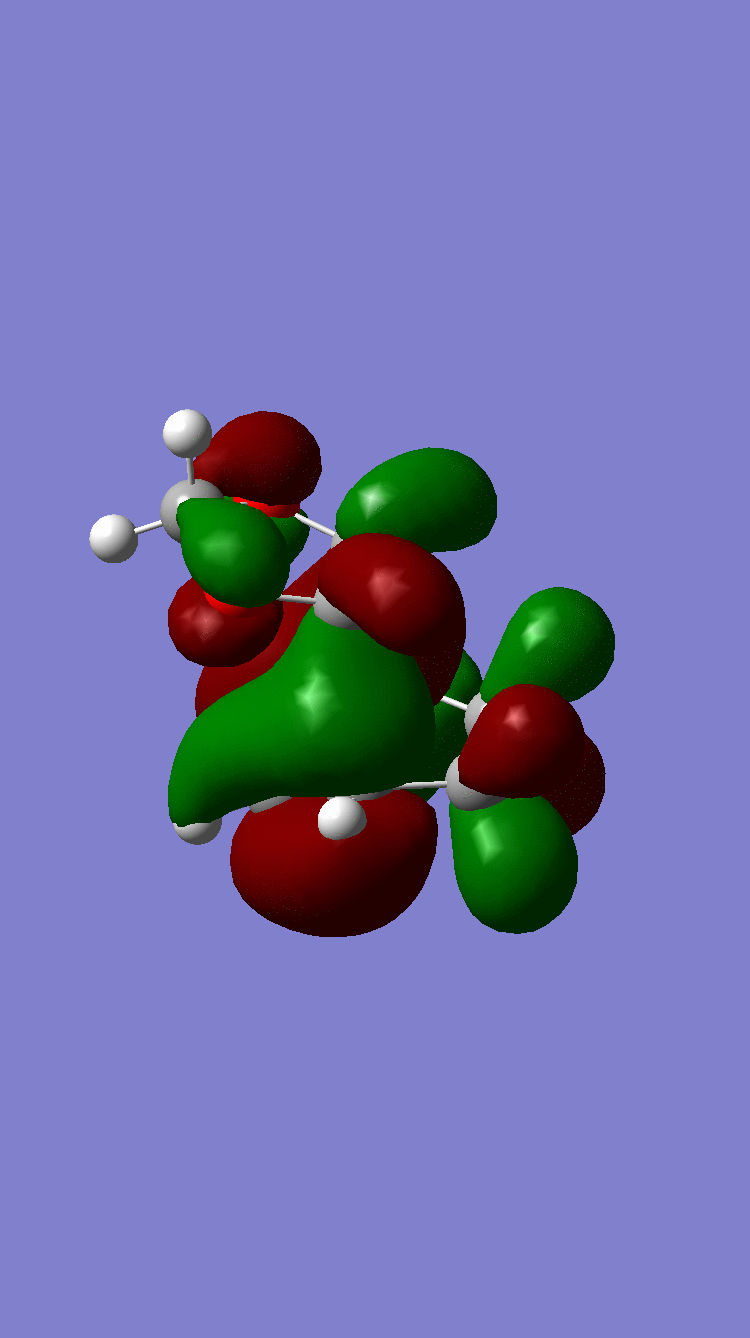 Antisymmetric Antisymmetric
|
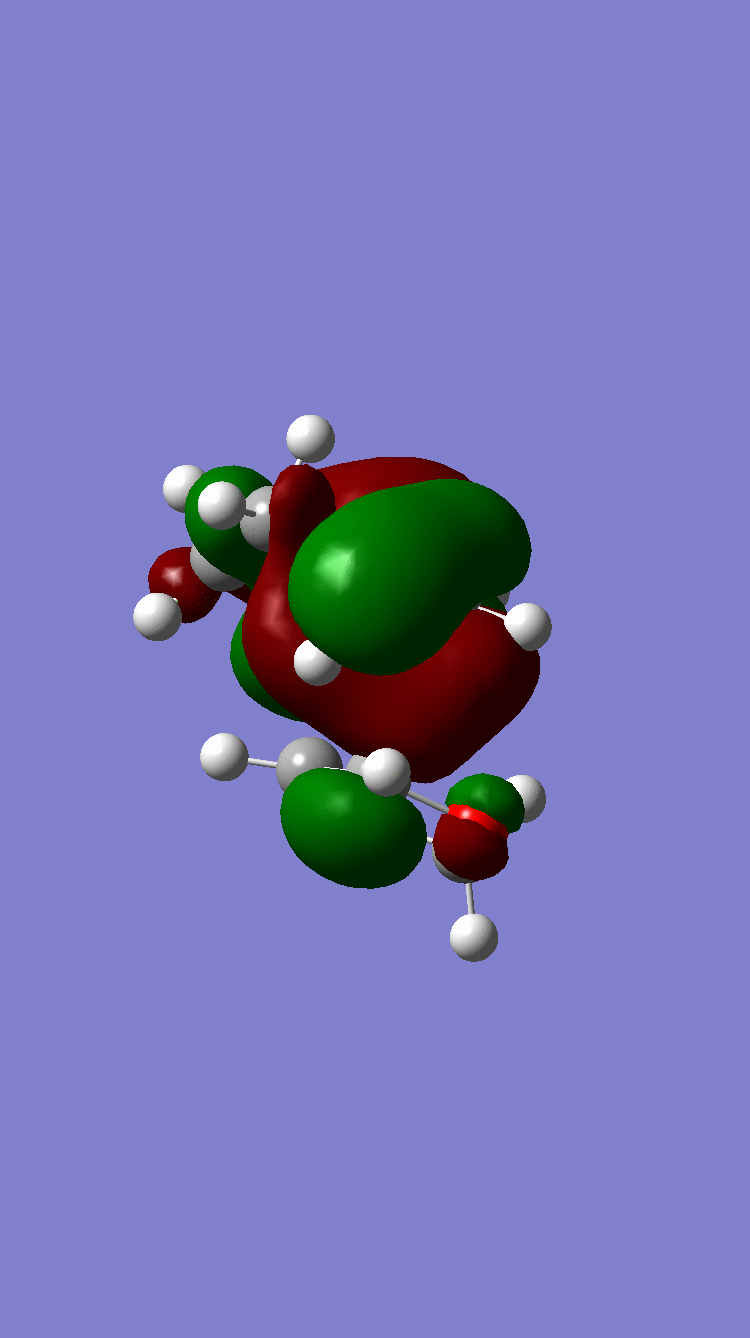 Antisymmetric Antisymmetric
|
(It's hard to see what's going on at these angles. The exo looks a bit off. Tam10 (talk) 14:16, 22 June 2017 (BST))
Because of the pi electron donating nature of the oxygens next to the C=C, the energy of the 1,3-dioxole increases, therefore the HOMO and LUMO of this dienophile are much higher than that of the ethylene present in exercise 1. Because of this increased energy, there is a much stronger interaction between the diene and the dienophile because the HOMO of the the dienophile and LUMO of the diene, both symmetric, are much closer in energy. This therefore leads to a much more energetically favourable reaction, because of the larger stabilisation energy, than that in exercise 1 and therefore occurs at a faster rate. This is said to be a inverse electron demand Diels-Alder reaction, in which an electron rich dienophile reacts with an electron poor diene. [6]
Thermochemistry
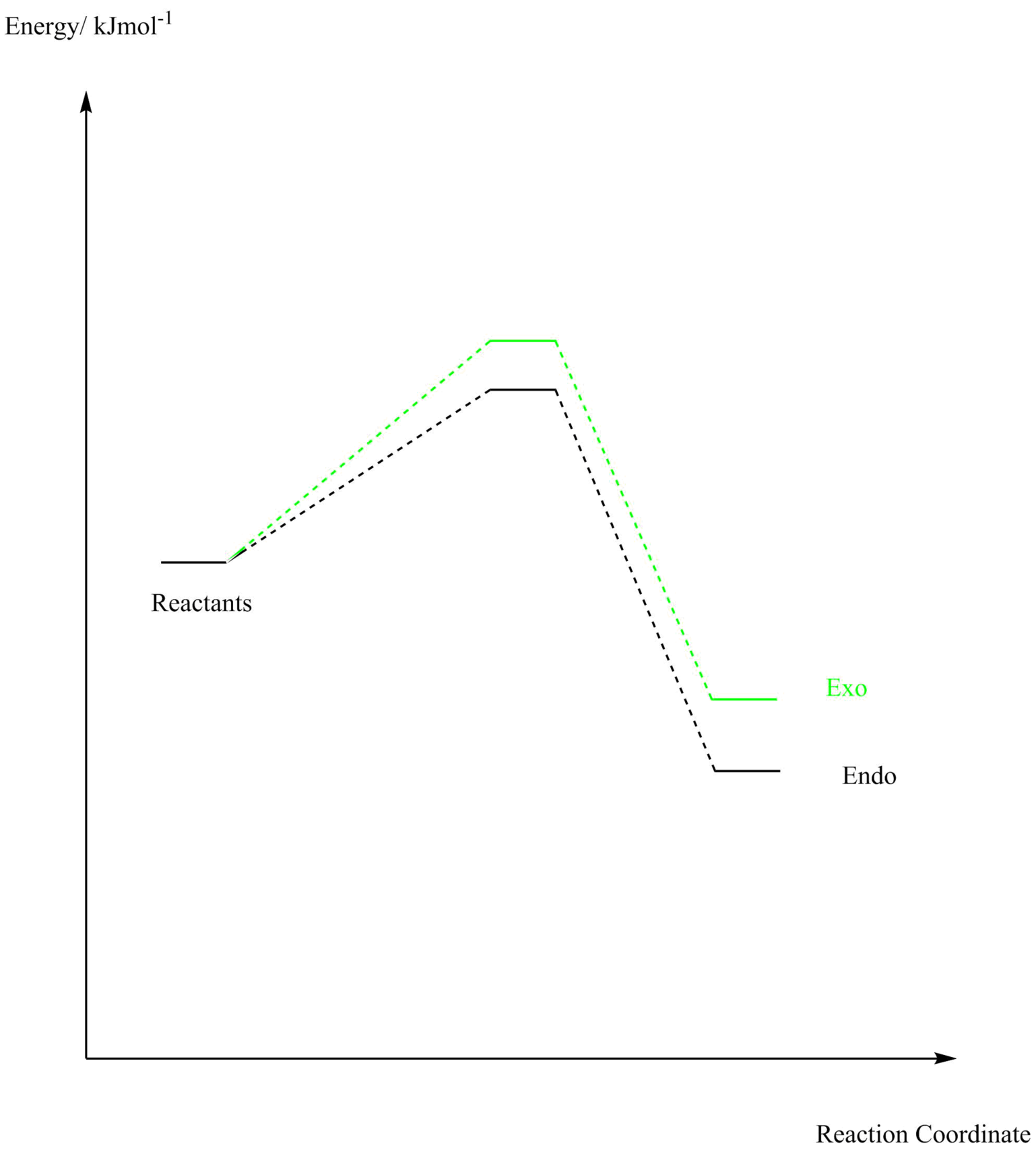
The reaction and energies and barriers for the reactants, transition states and products can be taken from the log files of each calculation undertaken. From the table and schematic below it is clear to see that both the reactions are exothermic, however the endo product has a much lower energy than that of the exo product, as well as having a lower reaction barrier. From this we can determine that the endo product is kinetically and thermodynamicaly favoured product.
Figure 9: Energy Profile Exercise 2
(Where's the data to support this image? How do they compare numerically Tam10 (talk) 14:16, 22 June 2017 (BST))
The endo product can be seen as the kinetically and thermodynamically favourable product because of the lower reaction barrier and lower energy of product, however this could also be due to steric and electronic factors.
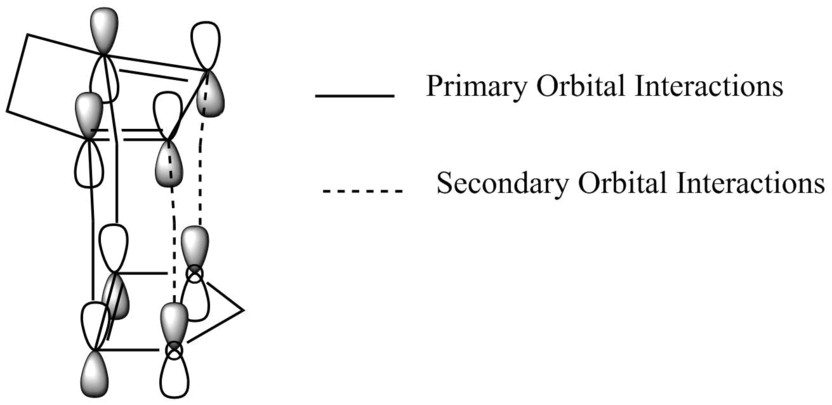
These steric and electronic factors are known as secondary orbital interactions, and in this case stabilise the endo transition state. The p-orbitals present on the diene are able to interact with the p-orbitals on the oxygen in the 1-3,dioxole dienophile. This lowers the energy of the transition state and in turn lowers the activation energy.
In the exo product there is clear steric clashes between the carbon atoms on the cyclohexadiene and the 1,3-dioxole, leading to destabilisation, these are not felt by the endo product.
Figure 10: Molecular Orbital Representation of Secondary Orbital Interactions in the endo pathway
Figure 11: Steric Clashes in the exo pathway'
Vibration Analysis and IRC
| Endo | Exo | |
|---|---|---|
| IRC | Concerted Synchronous | Concerted Synchronous |
| Vibration | 
|
|
Table 4: Vibrations and IRC for endo and exo pathways
Calculations Files
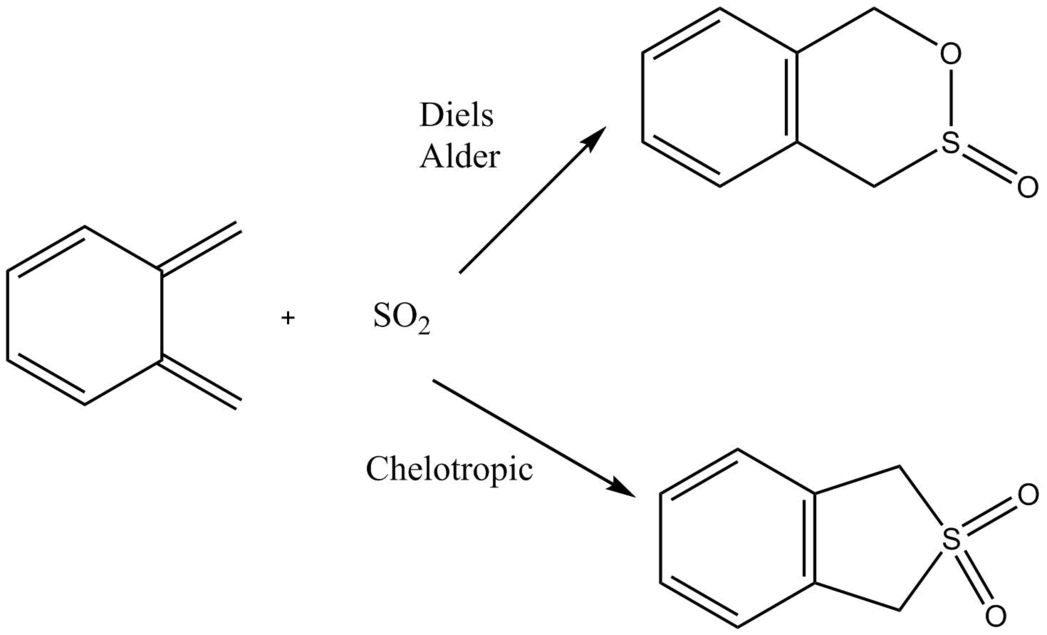
Exercise 3: Diels Alder vs Cheletropic
Figure 12: Exercise 3 Mechanism
Molecular Orbital Analysis
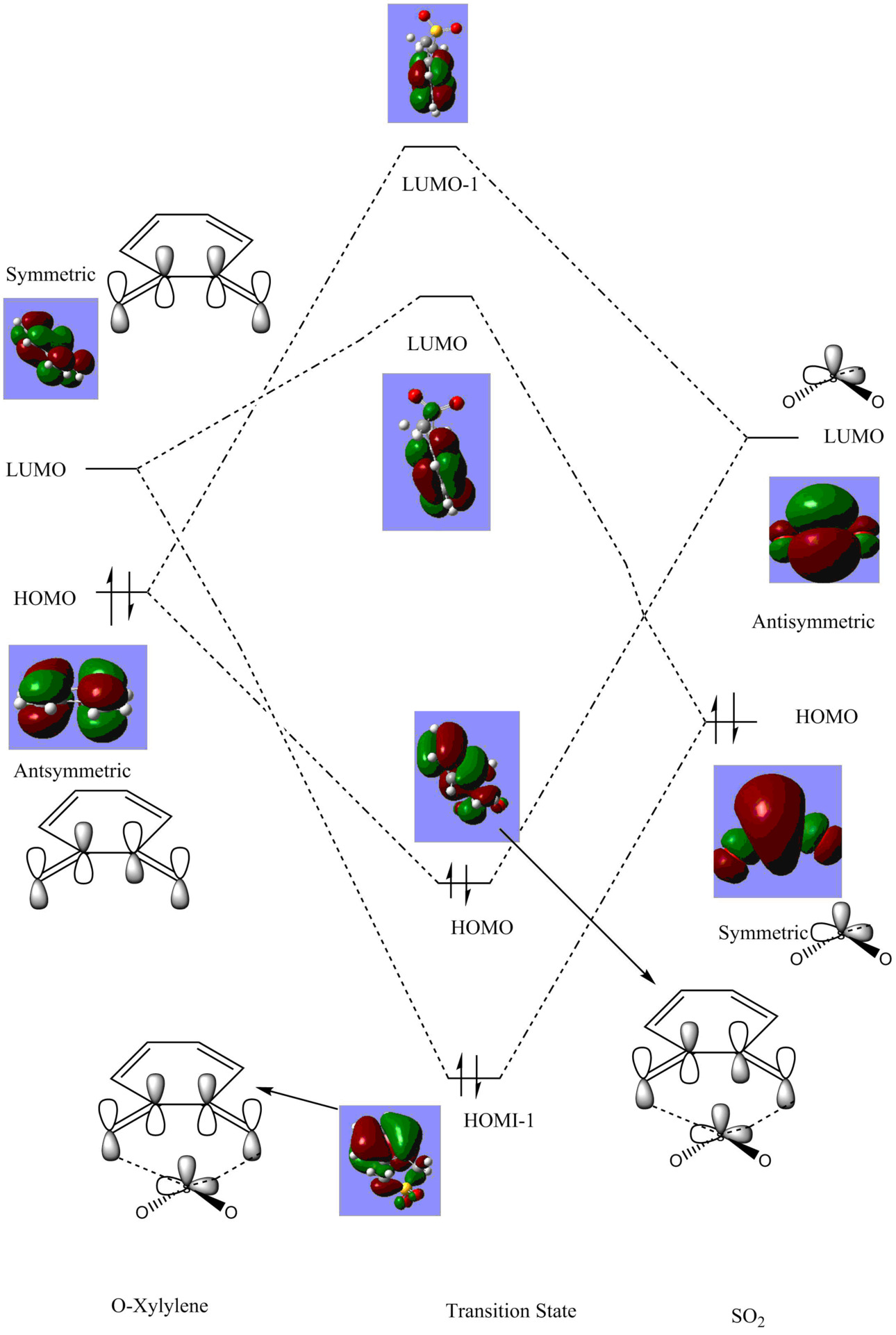
In this reaction o-xylylene was reacted with So2 in a Diels-Alder reaction forming an endo and exo product, such was the case in Exercises 1 and 2. However, because So2 is an electron deficient dienophile, its HOMO and LUMO energy levels are much lower than the dienophiles used in the earlier exercises. Because of this, this reaction occurs via a normal electron demand, due to a large energy gap between the HOMO of the diene and the LUMO of the dienophile. As well as the two Diels Alder reactions, a cheletropic reaction also takes place. A cheletropic reaction is defined as one that on one of the reagents both of the new bonds formed are to the same atom. [7]
Figure 13: Molecular Orbital Digaram for the Cheletropic Reaction Pathway
(The TS LUMO+1 doesn't look like there is any interaction with SO2 Tam10 (talk) 14:16, 22 June 2017 (BST))
Thermochemistry
| o-Xylylene/Hartrees | So2/Hartrees | Transition State/Hartrees | Product/Hartrees | Reaction Barrier/Hartrees | Reaction Energy/Hartrees | |
|---|---|---|---|---|---|---|
| Endo | 0.178816 | 0.118615 | 0.09056179 | 0.021695 | 0.03035179 | -0.038515 |
| Exo | 0.178816 | 0.118615 | 0.092078 | 0.021453 | 0.031868 | -0.038757 |
| Cheletropic | 0.178816 | 0.118615 | 0.099062 | 0.000002 | 0.038852 | -0.060208 |
| o-Xylylene/kJmol-1 | So2/kJmol-1 | Transition State/kJmol-1 | Product/kJmol-1 | Reaction Barrier/kJmol-1 | Reaction Energy/kJmol-1 | |
|---|---|---|---|---|---|---|
| Endo | 469.481444 | 311.423706 | 237.76999776 | 56.9602268 | 79.688630715 | -101.1211402 |
| Exo | 469.481444 | 311.423706 | 241.750807 | 56.3248558 | 83.6694404 | -101.7565113 |
| Cheletropic | 469.481444 | 311.423706 | 260.087301 | 0.0052510004 | 102.005934 | -158.076116 |
Table 5: Reaction Energies for Exercise 3
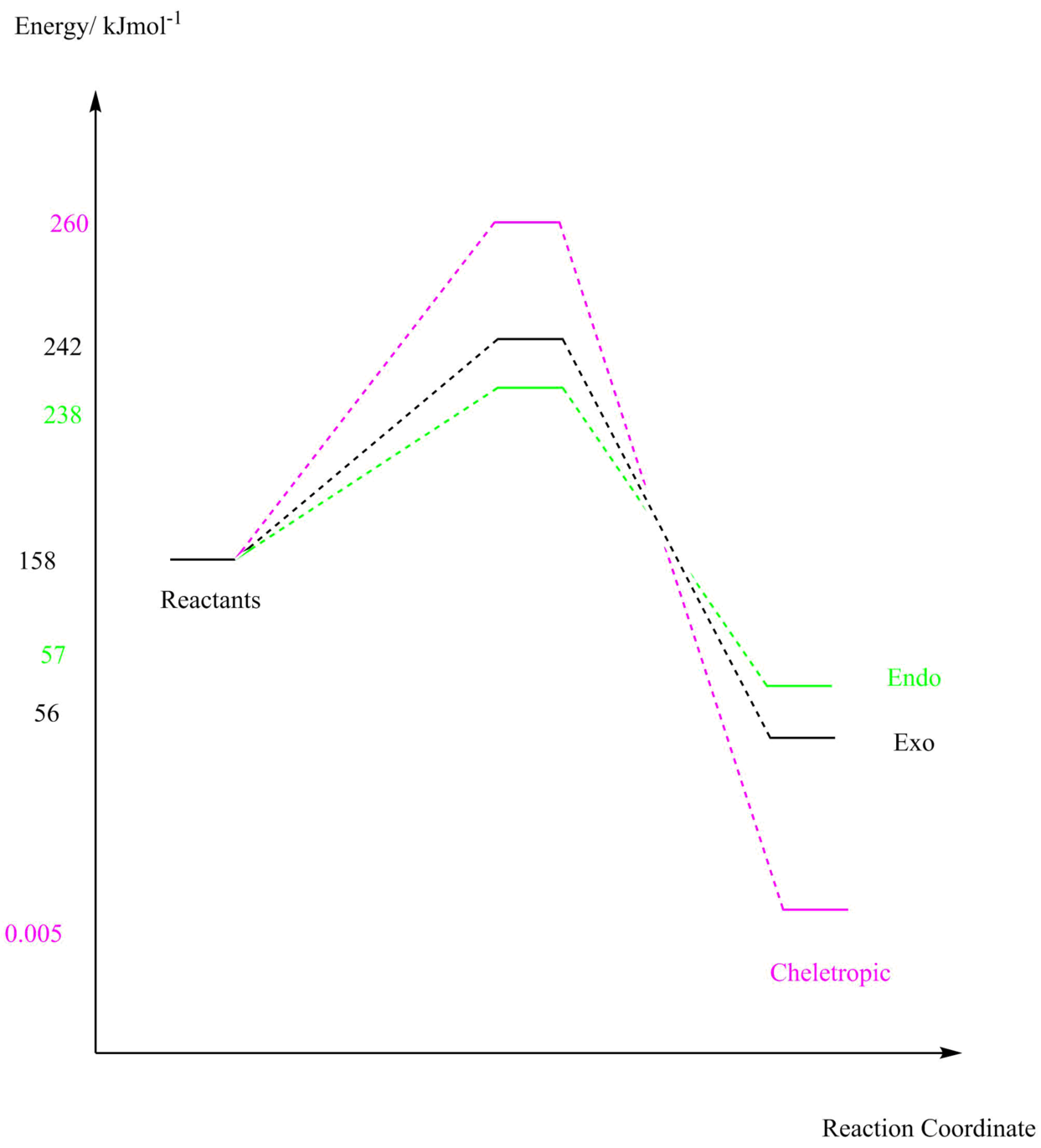
Figure 14: Energy profile for Exercise 3
(Why are these numbers on the left? They should also be normalised to the reactants Tam10 (talk) 14:16, 22 June 2017 (BST))
As shown from the tabulated data and the energy profile of the three potential pathways, the endo product is the most kinetically favourable product as it has the lowest energy transition state. The lowest energy product is that from the cheletropic product and therefore is the most thermodynamically favoured product. This is consistent with experimental data found in these reactions.
Vibration Analysis and IRC
| Diels Alder Endo | Diels Alder Exo | Cheletropic | |
|---|---|---|---|
| IRC | 
Concerted Asynchronous |

Concerted Asynchronous |
Concerted Synchronous |
| Vibration | 
334i cm-1 |

352i cm-1 |

487i cm-1 |
Table 6: Vibrational and IRC data for Exercise 3
From the table above it is clear to see that both Diels Alder reactions, exo and endo, exhibit asynchronous bond formation, the C-S bond is formed after the C-O bond. However in the cheletropic reaction both C-S bonds are formed at the same time, exhibiting synchronous bond formation.
Calculation Files
File:EX3 JB ENDO PRODUCT PM6.LOG
File:EX3 JB CHELOTROPIC PRODUCT PM6.LOG
File:EX3 JB CHELOTROPIC TS PM6.LOG
File:EX3 JB CHELOTROPIC IRC PM6.LOG
Conclusion
In the 3 Exercises, the three Diels Alder reactions were examined using the semi-empirical PM6 method and in Exercise 2 the geometries were optimised further using a basis set of B3LYP 6-31G(d) using the DFT method. In Exercise 3 a different type of pericyclic reaction, the cheletropic reaction, was introduced and investigated. Throughout all 3 Exercises, all reactants were optimised to a minima and then the respective transition states were optimised to first order saddle points. In Exercise 1, internuclear distance was shown to vary as the reaction proceeded. In Exercise 2, a direct comparison between exo and endo Diels Alder reactions were studied. This further lead to the rise of kinetic and thermodynamically favoured products also linking to secondary orbital interactions as well as steric effects. Finally in Exercise 3, it was demonstrated that percyclic reactions can proceed via synchronous or asynchronous concerted mechanisms completely dependent on the symmetry of the molecular orbitals of the reactants. In this circumstance, the cheletropic pathway was found to be synchronous concerted whilst exo and endo were found to be asynchronous concerted mechanisms.
References
<references>
- ↑ Cite error: Invalid
<ref>tag; no text was provided for refs namedPES Diagram - ↑ 2.0 2.1 Hückel Theory for Organic Chemists, C. A. Coulson, B. O'Leary and R. B. Mallion, Academic Press, 1978.
- ↑ 3.0 3.1 Levy, Mel (1979). "Universal variational functionals of electron densities, first-order density matrices, and natural spin-orbitals and solution of the v-representability problem". Proceedings of the National Academy of Sciences. United States National Academy of Sciences. 76 (12): 6062–6065. Bibcode:1979PNAS...76.6062L. doi:10.1073/pnas.76.12.6062
- ↑ 4.0 4.1 Dewar, M. J.; Olivella, S.; Stewart, J. J. (1986). "Mechanism of the Diels-Alder reaction: Reactions of butadiene with ethylene and cyanoethylenes". Journal of the American Chemical Society. 108 (19): 5771–5779. PMID 22175326. doi:10.1021/ja00279a018
- ↑ 5.0 5.1 Handbook of Chemistry & Physics (65th ed.). CRC Press. ISBN 0-8493-0465-2.
- ↑ 6.0 6.1 Bodwell, Graham J.; Zulan Pi; Ian R. Pottie (1999). "Electron Deficient Dienes. 2. One Step Synthesis of a Coumarin-Fused Electron Deficient Diene and its Inverse Electron Demand Diels–Alder Reactions with Enamines" (PDF). Synlett. 1999 (4): 477–479. doi:10.1055/s-1999-2645. Retrieved 31 March 2013.
- ↑ 7.0 7.1 Eric V. Anslyn and Dennis A. Dougherty Modern Physical Organic Chemistry University Science Books, 2006.
- ↑ Geometry optimization, Potential Energy Surface (PES) and Transition State Optimization in Gaussian 09 http://studynights.blogspot.co.uk/2015/03/geometry-optimization-potential-energy.html