Rep:Mod:Introduction to Modelling
Introduction to Modelling - Molecule Information
Ammonia - NH3
General Information
test molecule |
jmol link: File:AMIN NH3 OPTIMISED.LOG
Calculation method: RB3LYP
Basis set: 6-31G(d.p)
Final energy: -56.44297188 a.u.
RMS gradient: 0.05399560 a.u.
Point group: C3V
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
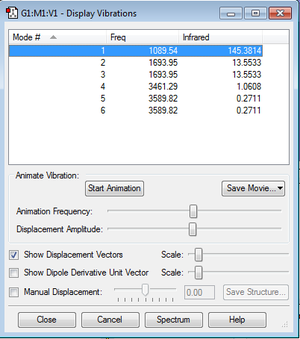
Vibration
Number of expected vibraton modes:
3N-6 is expected to give 3 vibration modes.
Degenerate modes:
Degenerate modes are #2-#3 and #5-#6 as they have the same vibration frequency.
Types of vibration displayed:
Modes 1,2 and 3 display bending vibrations whilst modes 4,5 and 6 display bond stretch vibrations.
Symmetry in vibration and "Umbrella mode":
Mode 4 and 1 both show high symmetry in vibrations. Mode 1 is known as the "umbrella" mode.
Number of expected IR peaks:
4 peaks are expected to appear in the IR spectrum due to 4 different absorption intensities.
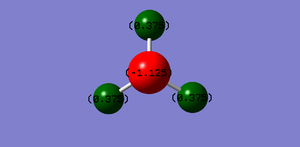
Atomic Charges
The N atom shows a negative charge at -1.125 and the hydrogen atoms show a positive charge of 0.375, implying that nitrogen is more electronegative thus the electrons reside in closer proximity to the nitrogen atom.
Nitrogen - N2
General Information
test molecule |
jmol link: File:AMIN N2 OPTIMISED.LOG
Calculation method: RB3LYP
Basis set: 6-31G(d.p)
Final Energy: -109.52412868 a.u.
RMS gradient: 0.00000060 a.u.
Point group: D∞h
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
Vibrations
N2 is a linear molecule with only one mode of vibration. Frequency: 2457.33
Hydrogen - H2
General Information
test molecule |
jmol link: File:AMIN H2 OPTIMISED.LOG
Calculation method: RB3LYP
Basis set: 6-31G(d.p)
Final Energy: -1.1785393 a.u.
RMS gradient: 0.00000017 a.u.
Point group: D∞h
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
Vibrations
H2 is a linear molecule with one mode of vibration. Frequency: 4465.68
The Haber Process Energies
E(NH3)= -56.55776873 a.u.
2*E(NH3)= -113.1155375 a.u.
E(N2)= -109.52412868 a.u.
E(H2)= -1.1785393 a.u.
3*E(H2)= -3.5356179 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -146.4789554 kJ/mol
The reaction is exothermic, therefore the product is expected to lie lower in energy (more stable).
Various values from different sources show an enthalpy change value of -92kJ/mol.[1-2] This is likely due to the different conditions used for the reaction and the nature of the calculations the programme GaussView calculates final energies of molecules.
Fluorine - F2
General Information
test molecule |
jmol link: File:AMIN F2 OPT.LOG
Calculation method: RB3LYP
Basis set: 6-31G(d.p)
Final Energy: -199.49825220 a.u.
RMS gradient: 0.00001139 a.u.
Point group: D∞h
Optimised bond length: 1.40292 A
Item Value Threshold Converged? Maximum Force 0.000041 0.000450 YES RMS Force 0.000041 0.000300 YES Maximum Displacement 0.000051 0.001800 YES RMS Displacement 0.000071 0.001200 YES
Vibrations
Fluorine is a diatomic molecule and only has one vibrational mode. There is no overall charge as both atoms are fluorine atoms, thus have the same electronegativity.
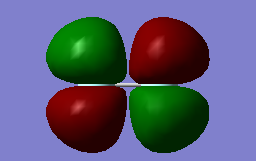
Molecular Orbitals
This diagram represent the HOMO (highest occupies molecular orbital) in a molecule of fluorine. This is the pi* orbital formed by the combination of 2p orbitals. The energy of this orbital is -0.39192 a.u. Two of this molecular orbital is formed as the number of atomic orbitals is equal to the number of molecular orbitals. Each holds 2 electrons and is filled. The presence of these molecular orbital alongside the pi molecular orbitals means that there is no pi bonding present in fluorine.
This diagram shows the LUMO (lowest unoccupied molecular orbital). This is the sigma* antibonding orbital formed from the combination of p-orbitals. This is the highest 2p molecular orbital in energy at -0.12687 a.u. The different colours shown in the diagram represent the phases of the molecular orbital, and it is clear that destructive interference is present due to out-of-phase components being adjacent.
This diagram displays the pi bonding orbital of fluorine, formed by 2p atomic orbitals. Constructive interference is shown clearly in this image as the pi-bonds are formed by atomic obritals being in-phase. Pi-bonding, however, is not present in the fluorine molecule due to the counter effect of the pi* antibonding orbital. Two equivalent pi bonding orbitals are formed. The energy of this MO is -0.52330 a.u.
This shows the first sigma antibonding molecular orbital formed by the combination of the 1s atomic orbitals. Energy of this orbital lies lower than the 2s molecular orbitals at -1.09050 a.u. (2s bonding energy = -0.58751 a.u.). Formation of antiboding is clear due to the out-of-phase atomic orbitals (shown in different colours) forming this MO.
This is the sigma bonding orbital and is the lowest energy molecular orbital formed in flourine at an energy of -1.33654. This MO is formed by the mixing of the 1s orbitals from each fluorine atom. Although this is a sigma orbital, the MO that forms the bond in F2 is the molecular orbital formed from the 2s AOs. This is because of the formation of an antibonding orbital alongside the bonding orbital in 1s mixing, whereas the antibonding MO formed by 2s does not contain electrons.
References
[1] Jim Clark, (2002). The Haber Process, http://www.chemguide.co.uk/physical/equilibria/haber.html (03/03/2017)
[2] Dr Phil Brown (2000-2017). The synthesis of ammonia - The Haber Process of Nitrogen Fixation, http://www.docbrown.info/page04/4_74revNH3c.htm (03/03/2017)