Rep:Mod:ISS7756
Inorganic Computational Lab Part 1
The purpose of the following exercises in part 1 of the computational lab was to gain familiarity with methods and calculations to be performed with Gaussian.
Initially, molecules of BH3, GaBr3, BBr3 were drawn, optimised and energies and bond lengths compared in order to assess the impact of changing ligands and centres in the above lewis acids.
A molecule of ammonia was also drawn and optimised, and later, the energy found was used in conjunction with the energy found for BH3 to find the energy of formation of ammonia-borane, a lewis acid/base adduct.
Creation and Optimisation of a Molecule of BH3
Method
A molecule of BH3 was drawn in Gaussview, with its bond distances manipulated to values of 1.51, 1.52 and 1.53Å. The molecule was then optimised using the B3LYP method with a 3-21G basis set. A link to the optimisation calculation can be found here. Using the optimised molecule obtained, a higher level basis set, a 6-31G(d,p) was then used to optimise the BH3 further, a link to which can be found here.
Analysis
The optimisation of the molecule was essentially a traverse along the Potential Energy Surface of the molecule, with energy as a funtion of distance. The optimised molecule therefore represented a minimum of this surface, where the gradient dE(R)/dR=0. It is important to note that the Born Oppenheimer approximation is evoked, essentially that the nuclei of the molecule are fixed, therefore energy was solely dependent on the frozen positions of the nuclei, with calculations being performed constantly with slight changes in the collective positions of the nuclei until a minimum was reached.
Upon optimisation using the 3-21G basis set, the bond distances and angles for the molecule of BH3 were found to be 1.19467, 1.19445, 1.19480Å, and 120.016o, 119.986o and 119.998o. The calculation performed was relatively simple and quick, yet still showed the expected D3h symmetry to 3 decimal places in the bond distances and 1 in the bond angles. Furthermore the bond distance calculated showed good agreement with a literature calculated value of 1.1867Å[1]. The summary of information obtained from the optimisation can be seen in the image on the right.
The job was confirmed to have completed upon analysis of the log file:
Furthermore, upon looking at graphs of the total energy and the RMS gradient, the energy gradient was seen to reach zero at optimisation step number 7.
Item Value Threshold Converged? Maximum Force 0.000220 0.000450 YES RMS Force 0.000106 0.000300 YES Maximum Displacement 0.000940 0.001800 YES RMS Displacement 0.000447 0.001200 YES Predicted change in Energy=-1.672478D-07 Optimization completed. -- Stationary point found.
Upon use of the 6-31G (d,p) basis set for optimisation, the calculation was observed to have worked by once again looking at the Item table of the log file, as before:
Item Value Threshold Converged? Maximum Force 0.000012 0.000450 YES RMS Force 0.000008 0.000300 YES Maximum Displacement 0.000061 0.001800 YES RMS Displacement 0.000038 0.001200 YES Predicted change in Energy=-1.069047D-09 Optimization completed. -- Stationary point found.
The bond lengths and bond angles calculated with the 6-31G(d,p) basis set were found to be 1.19231, 1.19232, 1.19231Å, with bond angles of 120.001o, 119.994o and 120.005o, again all consistent to 1dp in bond angles, however now to 4dp in bond lengths to a D3h symmetry. The energy was calculated to be -26.61532360au. The summary information can be found in the image to the left.
Creation and Optimisation of a Molecule of GaBr3
Method
A molecule of GaBr3 was drawn and the symmetry restricted to D3h with the tolerance at "very tight (0.0001)". An optimisation calculation was then performed using the B3LYP method with a LanL2DZ basis set. The optimisation file can be found here: DOI:10042/26199
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000003 0.001800 YES RMS Displacement 0.000002 0.001200 YES Predicted change in Energy=-1.282692D-12 Optimization completed. -- Stationary point found.
Analysis
Since both Br and Ga are heavier elements in the periodic table, this calculation used pseudo-potentials on the heavier elements in the molecule. Pseudo-potentials are used as a method of easier calculations for heavier elements, a way of modelling the "core" electrons of an atom since the chemistry of most atoms is in fact dominated by the interactions of valence electrons, hence the reason for groups in the periodic table: the general trends in reactivity based largely upon the number of electrons in their valence shells. Use of pseudo-potentials causes calculations to be much quicker.
Since the molecule was restricted to a D3h symmetry all bond distances were found to be 2.35018Å, with bond angles of 120.000o. The bond distance was compared to literature values and seen to have reasonable agreement as the literature reported a value of 2.277 Å[2]
Creation and Optimisation of BBr3
Method
The previously optimised molecule of BH3 using the 6-31G(d,p) basis set was opened and all H atoms were changed to Br atoms. The basis sets for all atoms were specified, namely that the B atom used the 6-31G(d,p) basis set, whereas pseudo potentials were used for the Br atoms (LanL2DZ as with the GaBr3 molecule). A link to the file is presented here: DOI:10042/26204
The item table once again showed the calculation to have completed:
Item Value Threshold Converged?
Maximum Force 0.000018 0.000450 YES
RMS Force 0.000010 0.000300 YES
Maximum Displacement 0.000112 0.001800 YES
RMS Displacement 0.000064 0.001200 YES
Predicted change in Energy=-2.260115D-09
Optimization completed.
-- Stationary point found.
Analysis
The bond distances calculated for BBr3 were 1.93397, 1.93393 and 1.93401 Å with bond angles of 120.001o, 119.997o and 120.002o. Therefore to the 3 dp agreement, the bond lengths were found to be 1.934 Å, with optimised bond angles of 120.00o to 2 dp, the 120o can essentially be seen as fixed in the trigonal planar arrangement with three substituents due to this being the furthest apart from each other the bromine atoms can be. Finally the energy was found to be a value of -64.43644911au. All information can be found in the summary table attached here.
Structural Comparisons BH3, BBr3 and GaBr3
| Molecule | M - X Bond Length (Å) |
| BH3 | 1.192 |
| BBr3 | 1.934 |
| GaBr3 | 2.35 |
Generally, as the ligand is increased in size, the bond length with boron increases. Furthermore, as the central boron atom is replaced with the larger gallium atom, whilst keeping the bromine ligand constant, the bond length again increases. Both observations may have been guessed using the general assumption: "more electrons equals larger atoms and therefore larger bond distances", however, the changes are can be seen to be not as uniform as may be expected and therefore the subject of interesting analysis.
Firstly, the bond lengths in BH3 and BBr3 shall be examined and compared. Firstly, both hydrogen and bromine have an unpaired electron in their ground states which can be used to form a bond with the sp2 hybridised boron (or gallium) centre. The boron-hydrogen bond in BH3 is seen to be substantially shorter than that of the boron-bromine bond in BBr3. This observation can be explained very simply in terms of the sizes of the ligands: hydrogen and bromine. Boron is found in period 2, meaning that its valence electrons reside in atomic orbitals with the orbital quantum number 2; therefore, bonding to the boron centre would involve the overlap of a ligand orbital with the 2sp2 orbitals of the boron. Overlap with the 1s electron of hydrogen therefore shows a much better energy match, with electrons in shells where n=1 and n=2, rather than overlaps with bromine where electrons are found in shells where n=2 and n=4 (for bromine).
However, it must be noted that bonding with bromine does in fact differ rather significantly from simple B-H bonds. Boron-halogen bonds in fact benefit from an extra degree of stabilisation due to the long pairs present on the halogen. The sp2 hybridised boron centre has an empty P orbital, perpendicular to the plane of the B-ligand bonds. Since all molecules analysed here can be termed "electron deficient", the bromine can act as a partial donor of electron density to relieve the electron deficiency of the central boron. In the explanation just given, it must be noted that boron can in these terms be seen as interchangeable with "gallium" or more generally, "group 3 element". This can be seen in the pictorial representation to the right. (Note: The other bromine lone pairs have been omitted from the picture for clarity)
However, there is a rather poor overlap with between the 2p orbital of the boron with the diffuse 4p orbital of bromine, therefore the interaction described can be considered largely insignificant with boron and bromine. The effect, however, becomes far more significant as better orbital overlaps are achieved, for example, in GaBr3. As Ga is also in period 4, the overlap between the Ga 4p and the Br 4p orbitals is far better and therefore the Ga-Br bond can be described as having a greater double bond character than the B-Br bond. This is manifested in the fact that although Ga is substantially larger than B, the M-Br bond is only larger by ~ 0.4 Å.
Frequency Analysis of BH3
Method
A frequency calculation was performed upon the optimised molecule of BH3 using the 6-31G(d,p) basis set. It was checked upon output that the energy was the same as that of the input file, therefore could be assumed that the structure remained unchanged. A link to the initial frequency analysis can be found here. The symmetry was then enabled to D3h, and the energy was only seen to differ in the final decimal place in comparison to the previous optimisation file. The summary can be found in the thumbnail on the left. Another frequency calculation was performed with the correct D3h symmetry as described just before. A link to the frequency analysis with the enabled symmetry can be found here.
The low frequency lines for the first frequency calculation were as follows:
Low frequencies --- -24.9985 -13.1089 -0.0006 -0.0004 0.0008 15.1347 Low frequencies --- 1162.9971 1213.0264 1213.1460
The low frequency lines for the second frequency calculation, when the correct symmetry was enabled, were as follows:
Low frequencies --- -5.0068 -1.2203 -0.0053 0.9880 9.0091 9.0914 Low frequencies --- 1162.9783 1213.1705 1213.1732
Analysis
| Number | Form of Vibration | Vibrational Frequency | Intensity | Symmetry in D3h Point Group |
| 1 |  H's move in and out of plane, B moves up as H's move down and vice versa |
1162.98 | 92.55 | A2 |
| 2 |  B-H unit moves down as H's in the BH2 unit separate |
1213.17 | 14.05 | E' (doubly degenerate) |
| 3 |  H's in BH2 unit move in unison clockwise as other H moves anticlockwise and vice versa |
1213.17 | 14.06 | E' (doubly degenerate) |
| 4 |  All H atoms move in and out in unison, B stays stationary |
2582.34 | 0.00 | A1' (totally symmetric) |
| 5 |  Asymmetric stretch H's in a BH2 unit |
2715.52 | 126.33 | E' (doubly degenerate) |
| 6 |  H's in BH2 unit stretch out as other B-H contracts |
2715.52 | 126.32 | E' (doubly degenerate) |
Frequency Analysis GaBr3
Just as before with BH3 molecule, however with the previously optimised GaBr3 molecule. The energy of GaBr3 was observed to be the same as before the frequency calculation was run with the pseudo potentials still being there, therefore the the calculation was assumed to be successful. A link to the frequency analysis can be found here DOI:10042/26213 .
Analysis
The low frequency information was found to be:
Low frequencies --- -0.5252 -0.5247 -0.0024 -0.0010 0.0235 1.2010 Low frequencies --- 76.3744 76.3753 99.6982
Similar stretches as with BH3 were found from the animations and therefore pictures shall not be included in the below table.
| Number | Description | Frequency | Intensity | Symmetry in D3h point group |
| 1 | 2 Br bend clockwise as the other bends anticlockwise and vice versa (as no. 3 for BH3) | 76.37 | 3.34 | E' |
| 2 | Ga-Br unit moves up as 2 Br's bend towards eachother (as no 2 for BH3) | 76.37 | 3.34 | E' |
| 3 | Ga moves up and down out of plane (as no 1 for BH3) | 99.70 | 9.22 | A2 |
| 4 | All Br's move in and out in unison (as no. 4 for BH3) | 197.34 | 0.00 | A1' |
| 5 | Asymmetric bend in a GaBr2 unit (as no. 5 for BH3) | 316.18 | 57.07 | E' |
| 6 | Ga-Br unit stretches as GaBr2 unit contracts (as no. 6 for BH3) | 316.18 | 57.07 | E' |
IR Spectra of both BH3 and GaBr3
IR spectra obtained for both molecules can be found below:
Although there are clearly 6 vibrations, only 3 are seen in the spectrum. It must be noted at the formula "3N-6" represents the maximum number of vibrations of a molecule, not how many peaks will necessarily be present in the IR spectrum. In an IR spectrum, only vibrations associated with a change in dipole will appear, therefore the symmetric stretch of the B-H bonds would not appear on the spectrum. Furthermore, it can be seen from the frequencies that 2 sets of stretches are degenerate.
Comparisons Between Vibrational Frequencies of BH3 and GaBr3
| symmetry in D3h | Vibrational Frequency BH3 | Vibrational Frequency GaBr3 |
| E' | 1213.17 | 76.37 |
| A2 | 1162.98 | 99.70 |
| A1' | 2582.34 | 197.34 |
| E' | 2715.52 | 316.19 |
The large differences in frequencies can be explained by the sizes of the atoms involved. The energy of the vibration is directly proportional to the frequency of oscillation. Since oscillation frequency is inversely proportional to μ, the reduced mass of the system, the larger the mass, the larger the reduced mass, and therefore the lower the oscillation frequency. The lower the oscillation frequency, the lower the energy. Therefore resulting in far lower vibrational frequencies of GaBr3 compared to BH3. There was also observed a reordering of vibrational modes, where in GaBr3 the E' modes were seen to be lower than the A2,,, opposite to the case in BH3.
The 2 IR spectra, however, cannot be described as entirely dissimilar. For example, the relative intensities of each of the peaks is the same in both spectra, with the lowest set of E' being the least intense, the A2,, the second least, and the highest frequency E' being significantly the largest in intensity. These can be seen to be in the ordering of the least significant change in dipole (the least intense) to the most significant change in dipole (the most intense - namely including an asymmetric stretch).
The energy levels can see to increase with the order of the orbitals in the MO diagram. A2,, and E', relatively close levels, at higher energies, and therefore not as tightly bound to the nuclei, are at lower frequencies, whereas the E' and A1' levels are more tightly bound to the nuclei, with lower energies, and therefore are observed at higher frequencies.
The same method and basis sets must be used for the optimisation and frequency analysis as the calculations are highly dependent upon the quality of the basis set used. If a better basis set was used, for example, in the frequency calculation, the error from the previous optimisation calculation would be carried forward. One can only gain information from the results is the same basis sets have been used on every molecule in the optimisation and frequency analysis. Furthermore, the frequency analysis essentially is a second derivative of the potential energy surface, with positive frequency values showing a minimum, the minimum of which was found using a certain basis set. With a different basis set, this minima may have changed, and therefore the frequency analysis would not work.
Frequency analysis allows for the confirmation that a minima on the potential energy surface has been found with the optimisation calculation. It is essentially a second derivative, with the frequency values as positive numbers showing the the fact that a minima has been reached (note: d2y/dx2 > 0, minimum, d2y/dx2 < 0, maximum. the second derivative being the change in curvature of the function). Along with a confirmation of minima, the frequency analysis also serves the purpose of computing vibrational modes, and computes IR and Raman spectra, allowing for comparison with experimental data.
Every molecule has 3N-6 vibrations, not all of which, of course, manifest themselves in the IR spectrum. the "-6" refer to the motions of the centre of mass of the molecule. For a stationary centre of mass, essentially that the centre of mass does not change in the vibration which is what we would expect in a vibration, the low frequencies should be as close to zero as possible.
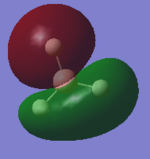
MO Analysis of BH3
The molecular orbitals of BH3 were computed, a link to the file can be found here DOI:10042/26236 . The HOMO and LUMO computed were then compared to LCAO MOs to assess the accuracy and usefulness of the LCAO approach. Pictorial representations of both can be found in the table.
| 'Real" (Computed) MO | LCAO MO | HOMO/LUMO? |
 |
 |
HOMO |
 |
|
HOMO |
 |
 |
LUMO |
It can be seen from the table that there is good agreement between the shapes of the HOMO and LUMO orbitals from LCAO and "Real" MOs, although there can be seen a slight, although not significant difference in the shape of one of the HOMOs. Therefore it can be concluded that LCAO gives a useful, although maybe not entirely accurate, picture of molecular orbitals in a simple picture.
NBO Analysis of NH3
Method
Firstly, a molecule of NH3 was drawn and optimised using the B3LYP method with a 6-31G(d,p) basis set, the link to the optimisation file can be found here. The energy was found to be -56.55776856au, with bond lengths of 1.018 Å and bond angles of 105.7o. Proof of convergence of optimisation can be found below:
Item Value Threshold Converged? Maximum Force 0.000024 0.000450 YES RMS Force 0.000012 0.000300 YES Maximum Displacement 0.000079 0.001800 YES RMS Displacement 0.000053 0.001200 YES Predicted change in Energy=-1.629712D-09 Optimization completed. -- Stationary point found.
A frequency analysis was then performed on the optimised molecule, a link to which can be found here. The low frequency lines of which are shown below:
Low frequencies --- -30.8045 0.0011 0.0012 0.0015 20.2188 28.2150 Low frequencies --- 1089.5530 1694.1235 1694.1861
As before, the symmetry was then corrected to C3v and the frequency analysis was performed again, the link to which can be found here. Again, the low frequency lines are displayed below:
Low frequencies --- -31.6906 -0.0019 -0.0017 -0.0011 13.0032 25.5425 Low frequencies --- 1089.5009 1694.1076 1694.1682
For both frequency analyses performed, it was confirmed that the energy of the NH3 remained constant. Furthermore, the low frequencies were observed to be quite low, with no negative frequencies, implying a minima had indeed been found. Finally, a population analysis was performed, a link to which can be found here. This file was then used for NBO analysis.
Analysis
The first image shows the NBO (natural bonding orbital) charge distribution with associated charge limites as -1.0-+1.0. The red shows a highly negative charge whereas green represents a highly positive charge. Therefore, as expected, the electronegative N is coloured red, with the more electropositive hydrogens appearing green. Below the coloured NBO image can be seen the specific numerical NBO charges which are -1.125 for N, and 0.375 for H.
Upon analysis of the .log file, more information can be gained on the nature and energies of the bonds.
From the information underneath the "bond orbit/ coefficient/ hybrids" heading, a more "organic" picture of the bonds can be seen. The hybridisation is shown where the N-H bonds are seen to comprise of a nitrogen orbital, with 75% p character and 25% s, namely, sp3 hybridisation, and 100% s character in the nature of the H orbital, with 69% contribution from the nitrogen atom and 31% contribution from the hydrogen atom to the bond; therefore showing the bond to be more "nitrogen-like" in character. This is also the case for the lone pair of nitrogen, which is 100% nitrogen based. Only the first part of the summary is shown below.
(Occupancy) Bond orbital/ Coefficients/ Hybrids --------------------------------------------------------------------------------- 1. (1.99909) BD ( 1) N 1 - H 2 ( 68.83%) 0.8297* N 1 s( 24.87%)p 3.02( 75.05%)d 0.00( 0.09%) -0.0001 -0.4986 -0.0059 0.0000 -0.2910 0.0052 0.8155 0.0277 0.0000 0.0000 0.0281 0.0000 0.0000 0.0032 0.0082 ( 31.17%) 0.5583* H 2 s( 99.91%)p 0.00( 0.09%) -0.9996 0.0000 0.0072 -0.0289 0.0000
Upon analysis of the "natural bond orbitals (summary)" section, the energies of all N-H bonds are seen to be the same, and in a region of 0--1 au. The core orbital of the nitrogen, the 1s, is seen to be far lower in energy at a value of -14 au, therefore a rationalisation of why core orbitals can be omitted from an MO diagram. Finally, the lone pair of the nitrogen is seen to be the highest in energy, and therefore a rationalisation of why this is the most reactive part of the molecule.
Natural Bond Orbitals (Summary): Principal Delocalizations NBO Occupancy Energy (geminal,vicinal,remote) ==================================================================================== Molecular unit 1 (H3N) 1. BD ( 1) N 1 - H 2 1.99909 -0.60417 2. BD ( 1) N 1 - H 3 1.99909 -0.60417 3. BD ( 1) N 1 - H 4 1.99909 -0.60416 4. CR ( 1) N 1 1.99982 -14.16768 5. LP ( 1) N 1 1.99721 -0.31756
Creation and Optimisation of NH3BH3
An ethane fragment was used initially to create a molecule of NH3BH3. Firstly, an initial optimisation calculation was run with the B3LYP method, with a 3-21G basis set. The calculation can be found here. The optimised molecule was then subjected to another optimisation with a higher basis set, namely the 6-31G(d,p), a link to the calculation can be found here DOI:10042/26303 , the energy was recorded at -83.22469028au.
Item Value Threshold Converged? Maximum Force 0.000137 0.000450 YES RMS Force 0.000038 0.000300 YES Maximum Displacement 0.001013 0.001800 YES RMS Displacement 0.000223 0.001200 YES Predicted change in Energy=-1.124439D-07 Optimization completed. -- Stationary point found.
A frequency analysis was also performed on the optimised molecule to ensure a minima had been reached. The energy was confirmed to remain the same in the summary section, and the low frequencies were indeed found to be low, with no negative vibrational frequencies. A link to the frequency calculation can be found here DOI:10042/26329 along with the low frequency lines shown below:
Low frequencies --- -8.8823 -0.0013 -0.0013 -0.0013 19.3700 19.5955 Low frequencies --- 263.3201 631.2465 638.5716
Association Energies: Ammonia-Borane
| Molecule | Energy (au) |
| BH3 | -26.61532360 |
| NH3 | -56.55776856 |
| NH3BH3 | -83.22469028 |
The energy difference is seen to be a value of -0.05159812au. This is equivalent to an energy change of -135.78 kJmol-1, showing formation of ammonia borane to be favourable as its energy is lower than of its constituent molecular fragments.
Inorganic Computational Lab Part Two: Ionic Liquids, Designer Solvents Mini Project
Creation and Optimisation of [N(CH3)4]+
Method
A molecule of [N(CH3)4]+ was drawn and Optimised using the B3LYP method with a 6-31G(d,p) basis set. The link to the optimisation calculation can be found here DOI:10042/26330 . The energy was found to be -214.18127262au. The bond lengths from the central nitrogen to the carbons of the ligands were seen to be between 1.5095-1.5096 Å, with bond angles of 109.5o.
Item Value Threshold Converged? Maximum Force 0.000074 0.000450 YES RMS Force 0.000017 0.000300 YES Maximum Displacement 0.001416 0.001800 YES RMS Displacement 0.000362 0.001200 YES Predicted change in Energy=-5.555862D-08 Optimization completed. -- Stationary point found.
A frequency calculation was also performed in order to confirm that a minima had been reached DOI:10042/26333 . The low frequencies calculated were seen to be low, with no negative frequencies and therefore confirming a minima had been reached.
Low frequencies --- -13.0294 -0.0010 -0.0006 -0.0005 6.1665 11.9572 Low frequencies --- 179.8930 278.8636 285.7089
Creation and Optimisation of [P(CH3)4]+
Method
A molecule of [P(CH3)4}+ was drawn and optimised using the B3LYP method with a 6-31G(d,p) basis set. The link to the optimisation calculation can be found here DOI:10042/26331 . The energy was found to be -500.82700313au. 3 of the bond lengths were found to lie at values of 1.8166 Å, with one lying at a slightly higher value of 1.8169 Å, however all near 1.817 Å. 2 of the bond angles were found to lie near to value of 109.5o.
Item Value Threshold Converged? Maximum Force 0.000148 0.000450 YES RMS Force 0.000033 0.000300 YES Maximum Displacement 0.000900 0.001800 YES RMS Displacement 0.000305 0.001200 YES Predicted change in Energy=-1.784699D-07 Optimization completed. -- Stationary point found.
A frequency calculation was also performed in order to confirm a minima had been reached DOI:10042/26334 . The low frequencies were observed to be low as well as the presence of no negative frequencies and therefore confirmation that a minima had been reached.
Low frequencies --- -16.5125 -0.0024 -0.0019 0.0010 4.9608 16.2249 Low frequencies --- 153.3784 183.0443 191.0015
Creation and Optimisation of [S(CH3)4]+
Method
A molecule of [S(CH3)4]+ was drawn and optimised using the B3LYP method with a 6-31G(d,p) basis set. The link to the optimisation calculation can be found here DOI:10042/26332 . The energy was found to be -557.53219535au. The bond angles and distances around the central sulphur were seen to be far more distorted than for the N and P counterparts. One of the S-C bonds was seen to be a value of 3.690 Å, with the others at values of 1.822 Å. Also, the bond angles were seen to be far from tetrahedral type values with angles of 77.4o, 2x102.6o and finally one of 180.0o.
Item Value Threshold Converged? Maximum Force 0.000035 0.000450 YES RMS Force 0.000010 0.000300 YES Maximum Displacement 0.000035 0.001800 YES RMS Displacement 0.000013 0.001200 YES Predicted change in Energy=-2.728916D-07 Optimization completed. -- Stationary point found.
A frequency calculation was also performed DOI:10042/26335 . The low frequencies again were observed to be low, with no negative vibrational frequencies confirming a minimum.
Low frequencies --- -36.5434 -30.6695 -18.6906 -0.0019 -0.0014 0.0017 Low frequencies --- 2.4264 17.7747 53.3374
Comparisons in Structures of the 3 Cations
Bond Lengths to the Central Atom
| Bond | Length (Å) |
| N-C | 1.51 |
| P-C | 1.82 |
| S-C | 1.82 (x3), 3.69 |
Variances in NBO Charge Analysis
| Complex | Atom | Charge |
| [N(CH3)4]+ | N | -0.295 |
| C | -0.483 | |
| H | 0.260 | |
| [P(CH3)4]+ | P | 1.667 |
| C | -1.050 | |
| H | 0.298 | |
| [S(CH3)4]+ | S | 0.915 |
| C | -0.842(x3), -0.581 | |
| H | -0.276 - -0.295(x9), 0.200(x3) |
Creation and Optimisation of [N(CH3)3(CH2OH)]+
Firstly, a molecule of [N(CH3)3(CH2OH]+ was drawn and optimised using the B3LYP method with a 6-31G(d,p) basis set DOI:10042/26346 . An energy of -289.39323120au was found. Furthermore, the item table showed that the optimisation had converged.
Item Value Threshold Converged?
Maximum Force 0.000056 0.000450 YES
RMS Force 0.000009 0.000300 YES
Maximum Displacement 0.000361 0.001800 YES
RMS Displacement 0.000103 0.001200 YES
Predicted change in Energy=-1.576530D-08
Optimization completed.
-- Stationary point found.
Unfortunately, the frequency analysis showed a negative vibrational frequency and therefore showed a minimum had not been reached. Both the optimisation calculation and frequency analysis were run again, yet still a negative vibrational frequency was obtained.
Creation and Optimisation of [N(CH3)3(CH2CN)]+
A molecule of [N(CH3)3(CH2CN)]+ was drawn and optimised using a B3LYP method with a 6-31G(d,p) basis set DOI:10042/26352 . The energy was found at a value of -306.39376846au. The iten table showed that the optimisation had converged.
Item Value Threshold Converged?
Maximum Force 0.000141 0.000450 YES
RMS Force 0.000026 0.000300 YES
Maximum Displacement 0.001794 0.001800 YES
RMS Displacement 0.000491 0.001200 YES
Predicted change in Energy=-1.965716D-07
Optimization completed.
-- Stationary point found.
A frequency analysis was also performed DOI:10042/26466 and found to have reached a minimum, with low values for the low frequencies.
Low frequencies --- -11.6949 -0.0007 -0.0007 0.0005 7.9226 13.2068 Low frequencies --- 91.6093 154.0073 210.0755
References
<references>
- ↑ M. S. Schuuman, W. D Allen and A. F. Scaefer III, "The an initio limit quartic function force field of BH3", J. Comp. Chem., 2005, 26, 1106-1112.DOI:10.1002/jcc.20238
- ↑ D. Dai and K. Balasubramanian, "Geometries and Potential Energies of Electronic States of GaX2 and GaX3 (X=Cl, Br and I)", J. Chem. Phys, 1993, 99, 293.DOI:10.063/1.465807