Rep:Mod:IR511(P)
Physical Chemistry Computational Experiment
In this computational investigation, transition structures for two different reactions, the Cope rearrangement and the Diels Alder cycloaddition, were characterised on potential energy surfaces. Unlike the dynamics calculations that can be made for simple molecules (e.g. diatomics) using model potential energy surfaces, molecular mechanics methods cannot be applied to study transition states of larger molecules. The molecules in this investigation were thus be analysed using molecular orbital-based methods, where transition structures are located based on the local shape of a potential energy surface.
The Cope Rearrangement
The Cope Rearrangement of 1,5-hexadiene
The Cope Rearrangement of 1,5-hexadiene is an example of a [3,3] sigmatropic rearrangement. There are two minimum energy conformations for the molecule, having an anti-periplanar and gauche geometry respectively. In addition, different higher energy conformations exist; free rotation about C-C single bonds allows for interconversion between these. The rearrangement, displayed below, occurs in a concerted fashion via either a chair or boat transition state structure. In the following tutorial the lowest energy conformer of 1,5-hexadiene was determined using the computer modelling programme Gaussian to calculate activation energies and enthalpies, allowing for the determination of the preferred mechanism of reaction.
| Cope Rearrangement of 1,5-hexadiene |
Optimising the reactants and products
Based on a consideration of sterics it would generally be expected that the app conformer (central dihedral angle of 180°) is lower in energy than the gauche conformer (dihedral angle of 60°). Using GaussView, input files for each structure were created and submitted to Gaussian for a structure optimisation at the HF/3-21G level of theory (Hartree Fock and basis set 3-21G). The Hartree Fock basis set takes the average of a molecule's exchange energies over all of its electronic wavefunctions. It thus provides information on the physical quantities of a molecule on a very basic level.[1]
The obtained optimised structures were compared based on their electronic energies and symmetry point groups:
| Linkage | Final energy (a.u.) | Point group | Name | File |
|---|---|---|---|---|
| Anti | -231.69253528 | Ci | anti 2 | LOG |
| Gauche | -231.69266122 | C1 | gauche 3 | LOG |
Despite being very close in energy, this result contradicts the initial hypoythesis of the app/anti linkage being more favourable and lower in energy. A likely reason for this observation is the fact that the HF/3-21G level does not take all electronic interactions (stabilisation due to conjugation etc.) into account. The two conformations were thus reoptimised at a higher level of theory basis set; B3LYP/6-31G*. The B3LYP method accounts for effects related to electronic interactions as it includes DFT (density functional methods). The electronic energies obtained are more accurate and indeed provide the expected relative energy for the anti and gauche linkage that is in line with the result proposed by Woodward and Hoffmann.[2]
| Linkage | Final energy (a.u.) | Point group | Name | File |
|---|---|---|---|---|
| Anti | -234.61170280 | Ci | anti 2 | LOG |
| Gauche | -234.61132934 | C1 | gauche 3 | LOG |
Finding the lowest energy conformation
Two further optimisations were performed, again at the HF/3-21G level of theory. The dihedral angles for the terminal four carbon atoms were adjusted each time, giving rise to different conformations.
| Linkage | Final energy (a.u.) | Point group | Name in appendix 1 |
|---|---|---|---|
| Gauche | -231.69153029 | C2 | gauche 4 |
| Gauche | -231.68961575 | C1 | gauche 5 |
 |
 |
Investigation of the anti 2 conformation
The optimised anti 2 conformer was then investigated further. Following an initial result for electronic energy of -231.692535 a.u. for the HF/3-21G basis set, the energy decreased by almost 3 a.u. to -234.611702 a.u. when reoptimising at the higher B3LYP/6-31G* level. As explained above, the geometry of the reoptimised molecule corresponds to a closer match with reality. Models of the two molecules, including the display of bond lengths, are given below.
Shiprecusor21 |
Shiprecusor21 |
Whilst bond angles differ only slightly, a trend regarding bond lengths was observed: The higher optimised molecule displayed longer C=C and shorter C-C bonds than the less optimised molecule:
| Level of optimisation | Double bond length | C2-C3, C4-C5 bond length | Central single bond length | Dihedral angle |
|---|---|---|---|---|
| HF/3-21G LOG | 1.31614 | 1.50881 | 1.55288 | -179.95080 |
| B3LYP/6-31G* LOG | 1.33358 | 1.50417 | 1.54814 | -179.95482 |
Frequency analysis
All the electronic energies obtained from the output files so far correspond to the energy of the molecule on the bare potential energy surface only and can thus not be compared to experimental values. Additional terms, given by a frequency calculation, are required. This calculation was performed for the previously optimised anti 2 conformer. The structure represents an energy minimum and hence all vibrational frequencies are real (positive). (LOG HF)
| Type of energy (kcal/mol) | Associated equation | Energy (a.u.) |
|---|---|---|
| Sum of electronic and zero-point energies at 0 K | E = Eelec + ZPE | -234.469207 |
| Sum of electronic and thermal energies | E = E + Evib + Erot + Etrans | -234.461864 |
| Sum of electronic and thermal enthalpies | H = E + RT | -234.460920 |
| Sum of electronic and thermal free energies | G = H - TS | -234.500770 |
Transition state structures
Transition structure optimisations, for both the "chair" and "boat" geometries, were then performed using three different ways:
- Computation of the force constant matrix
- Freezing the reaction coordinate by using the Redundant coordinate editor
- Using the QST2 Method by specifying reactant and product molecules to interpolate the transition state geometry
Having identified the minimum energy geometries for both states the Intrinsic reaction coordinate (IRC) method will be used to determine the conformer of 1,5-hexadiene each transition state will form.
"Chair" Transition Structure
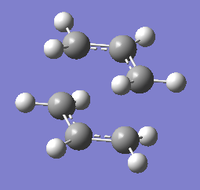
Firstly, the chair transition state, consisting of two C3H5 allyl fragments with C2h symmetry, was analysed. To do so, two optimised identical allyl fragments (HF/3-21G level of theory) were oriented approximately 2.2A apart, ensuring an eclipsed arrangement for the terminal carbons (shown on the right). Since the exact geometry of the transition state is unknown this structure represents a guess only.
Using method 1, the force constant matrix, it had to be assumed that the guess structure for the transition state constitutes a close match to the geometry of the actual structure: In order to compute the force constant matrix (Hessian), the negative direction of curvature (i.e. the reaction coordinate) needs to be clearly defined.
A transition state optimization for the guess structure was set up by selecting Opt+Freq and setting the calculation to a TS (Berny). The force constant was calculated exactly once; the frequency calculation yielded an imaginary frequency of -817.75 cm-1 and the corresponding animation, showing bond vibrations, is shown below. This frequency of vibration corresponds exactly to this particular bond forming/ breaking reaction. (LOG)
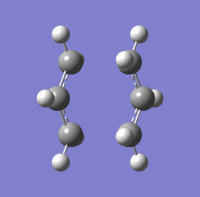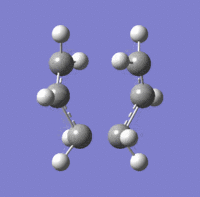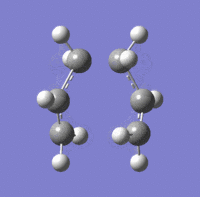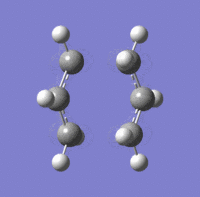
A second method to derive at this optimised structure by using the redundant coordinate editor in conjunction with the same guess structure for the transition state was tested. The terminal carbon distance at either end of the eclipsed allyl fragments were frozen (i.e. to freeze the reaction coordinate), doing so allowed for an initial optimisation of the rest of the molecule. Differentiating along the reaction coordinate does thus not require a computation of the whole force constant matrix.
The optimization was then compared to the structure obtained from using method 1. As expected, the structures of the two molecules were similar, only that the bond forming/breaking carbon distances in the second molecule were fixed to 2.2Å. The bonds were then unfrozen and a transition state optimisation (TS (Berny)) was run, yielding exactly one imaginary frequency at -817.89cm-1 (LOG). This arises from the fact that the transition state corresponds to the only maximum (negative concavity, negative second derivative) along the reaction coordinate.
The bond making/breaking distances in the transition state obtained using method 1 were 2.02017Å, compared to 2.02075Å in the transition state optimised using the redundant coordinate editor. The high level of similarity for the two differently optimised molecules suggests that the guess structure used indeed provides a close match with the actual geometry of the transition state. If this would not be the case, the computation of the force constant matrix (Hessian) in method 1 would not have yielded a similar result to the one obtained by differentiating along the reaction coordinate in method 2. Both methods are thus reliable in terms of arriving at the same optimised chair transition state. Each optimised structure gave rise to one imaginary frequency around -818cm-1 only; the conditions for a transition state are fulfilled.
"Boat" Transition Structure
The QST2 method was used to optimise the "boat" transition state. This method works based on the specification of reactants and products and the calculation then interpolates between the two geometries to find the transition state between them. The only requirement using this method is that both the reactant and product molecule must be numbered in the same way, before and after the rearrangement. This was done for the anti 2 structure:
| Reactant | Product |
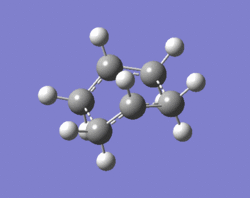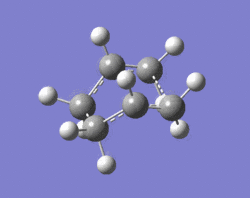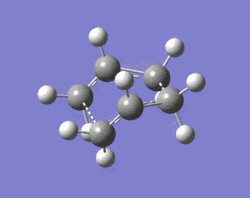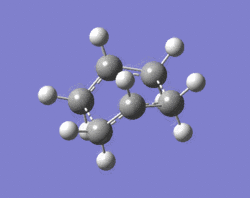
The QST2 calculation was set up to an optimisation of the transition state (TS (QST2)). This calculation, however, is unsuccessful which suggests that the reactants and products in the input file are not close enough to the actual transition structure. LOG
It was thus necessary to modify the reactant and product geometries manually so that they resemble the "boat" structure and a second minimisation was run, in which the two allyl fragments converged to the "boat" structure (LOG). The fact that the optimised structure state was indeed the transition state geometry was verified by the fact that only one imaginary frequency existed (-840.05cm-1), an animation of the bond vibration in the transition state is shown below.
It is thus apparent that the rearrangement of the anti 2 structure can pass via the boat transition state. It cannot be claimed that this is exclusively the case as the geometries of reactant and product molecules had to be manipulated for this observation to be made.
IRC Method
Simply based on the geometry of the "boat" and "chair" transition state it was not possible to predict the conformation of 1,5-hexadiene formed. Using the IRC Method (Intrinisic Reaction Coordinate), the minimum energy path (i.e. where the potential energy surface is the steepest) from a given transition state can be followed down into the product channel. "Snapshots" of the structure's geometry are taken along the path at different steps and allow for a determination of the lowest energy structure formed from a particular transition state.
The IRC method was tested on the optimised chair transition state that was obtained using the frozen coordinate method; the computation was run in the forward direction only (symmetrical reaction pathway, meaning that both the reactant and product channel are identical) and the force constant was calculated at every step along the IRC. Once the computation had run a chk file with all intermediate molecular structures was obtained (LOG). Contrary to the specified 50 points only a total of 44 steps were recorded, indicating that the computation had identified an energy minimum earlier than expected. This prediction was verified by an inspection of the gradient and energy.
 |
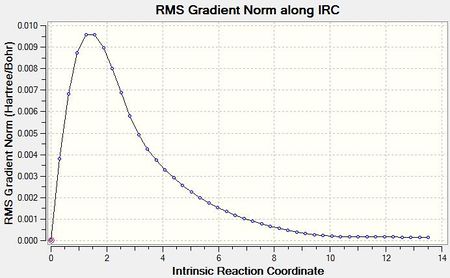 |
Since the last step on the IRC corresponds to a step in the reaction coordinate that is closest to the product conformation, an optimisation using this point as input file for Gaussian was run and the geometry of the resulting molecule (LOG) was compared to the original minimum energy conformer generated in the IRC (step 44). Despite their identical visual appearance, a comparison of bond angles and lengths suggested slight differences in the two geometries.
| Level of optimisation | Central dihedral angle | C1-C2, C5-C6 double bond length | C2-C3, C4-C5 single bond length | C3-C4 central single bond |
|---|---|---|---|---|
| Step 44 on IRC | -67.19115 | 1.31583 | 1.50789 | 1.55249 |
| Optimised step 44 | -64.16940 | 1.31566 | 1.50829 | 1.55082 |
From the table it can be seen that the further optimised structure approaches a 60° angle characteristic for a "gauche" conformation. This suggests that the rearrangement of the "gauche" conformer can proceed via the chair transition state. The further optimised step 44 represents a closer match to reality, from its energy -231.69166702 a.u. and point group C2 it follows that this geometry corresponds to gauche 2 in appendix 1. The fact that this conformation indeed corresponds to an energy minimum was verified by the log file, specifying that a stationary point had been reached:
Item Value Threshold Converged? Maximum Force 0.000010 0.000450 YES RMS Force 0.000003 0.000300 YES Maximum Displacement 0.000298 0.001800 YES RMS Displacement 0.000091 0.001200 YES Predicted change in Energy=-2.411150D-09 Optimization completed. -- Stationary point found.
The same IRC calculation was performed for the "boat" transition state that had previously been optimised using the QST2 method. Initially, however, a minimum energy conformation was not reached within the specified number of 50 steps. The calculation was run again, selecting 100 steps this time and the resulting minimum energy structure was obtained after 75 steps. The molecule was minimised to the gauche 3 conformation. LOG
Calculating activation energies
In the last part of the tutorial it was envisaged to calculate the activation energy of the Cope Rearrangement via each of the two transition states. Both geometries were optimised at higher level of theory B3LYP/6-31G* and frequency calculations were performed in order to to obtain thermodynamic data. (LOG chair HF, LOG boat HF, LOG chair B3LYP, LOG boat B3LYP)
The results are tabulated below (using the table from the script as template).
Summary of energies (in hartree)
| HF/3-21G | B3LYP/6-31G* | |||||
|---|---|---|---|---|---|---|
| Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | |
| at 0 K | at 298.15 K | at 0 K | at 298.15 K | |||
| Chair TS | -231.619322 | -231.466706 | -231.461346 | -234.556983 | -234.414924 | -234.409004 |
| Boat TS | -231.602845 | -231.450928 | -231.445299 | -234.543093 | -234.402342 | -234.396008 |
| Reactant (anti2) | -231.692535 | -231.539540 | -231.532567 | -234.611710 | -234.469207 | -234.461864 |
1 hartree = 627.509 kcal/mol
Summary of activation energies (kcal/mol)
| HF/3-21G | HF/3-21G | B3LYP/6-31G* | B3LYP/6-31G* | Experimental [3] | |
| at 0 K | at 298.15 K | at 0 K | at 298.15 K | at 0 K | |
| ΔE (Chair) | 45.70 | 44.69 | 34.06 | 33.17 | 33.5 ± 0.5 |
| ΔE (Boat) | 55.60 | 54.76 | 41.96 | 41.33 | 44.7 ± 2.0 |
The Diels Alder Cycloaddition
The Diels Alder reaction is an important [4+2] cycloaddition; a type of concerted pericyclic rearrangement which leads to the formation of two sigma and one new π bond. The reaction was first described by the Germans Otto Diels and Kurt Alder, an achievement for which they were awarded the Nobel Prize in Chemistry in 1950. The reaction, which provides a reliable method for the formation of six-membered cyclic ring systems is particularly favoured if it proceeds between an electron rich diene and an electron poor dienophile (alkene). According to the Woodward-Hoffmann selection rules this (4n+2)π electron reaction proceeds thermally with all suprafacial components, meaning that the bonds are formed on the same face of the π-system.[4] Diels-Alder reactions are usually under kinetic control and thus yield the fastest formed product via the lowest energy transition state.
Reaction of cis-butadiene and ethene
The most basic Diels-Alder reaction is the [4+2] cycloaddition between cis-butadiene and ethene to form cyclohexene. Neither reactant has a substituent with electronic demands and thus stereoselectivity does not need to be considered. The two reactants were optimised using the AM1 semi-empirical molecular orbital method and examining their HOMO and LUMO symmetries (LOG cis-butadiene, LOG ethene). These molecular orbitals are of particular importance as the reaction is governed by frontier molecular orbital (FOMO) symmetry. Unless specified otherwise, the relatively lower AM1 level of theory was be used throughout this exercise to optimise reactant molecules as the high level result provided by the HF and B3LYP basis sets as in the previous exercise are not required here. In fact, the level of optimisation would potentially be too high, as the increase in optimisation leads to bend structures that are unsuitable for a molecular orbital discussion. Flat structures are preferred in order to illustrate orbital interactions in the most meaningful way.
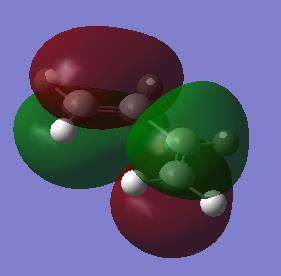
The AM1 optimisation of cis-butadiene gave the following results:
|
 |
 |
 |
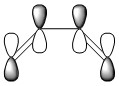 |
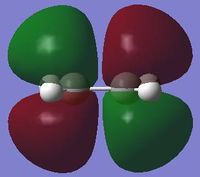
With respect to a plane of symmetry passing through the central bond and perpendicular to the plane of the molecule, the HOMO of cis-butadiene is asymmetric (a) and the LUMO symmetric (s). The opposite symmetry was observed for ethene:
|
 |
 |
Optimising the transition structure of the prototype reaction
These optimised structures were then used to compute the transition state for the reaction between butadiene and ethene. The dienophile is thought to approach butadiene from above to allow for maximum overlap of the interacting HOMO-LUMO orbitals. A requirement for a successful reaction is that reacting orbitals need to be of the same symmetry.

The transition state corresponding to this reaction was computed and analysed with respect to bond lengths and orbital symmetry. This was achieved by computing the force constants at the beginning of the calculation. As done previously in the Cope Rearrangement, a guess structure for the transition state was created by arranging the carbon atoms involved in the bond formation approximately 2.2A apart. The guess structure was firstly optimised at the AM1 level, then further using the B3LYP/6-31G* basis set (LOG AM1, LOG B3LYP/6-31G*). The results of these calculations, showing the expected asymmetry of the HOMO, are displayed below.
|
 |
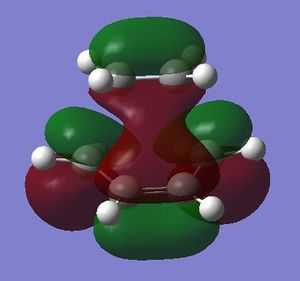 |
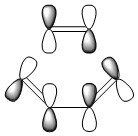
From the MO illustration above it follows that the transition state HOMO is asymmetric; this results from an interaction between the HOMO (a) of cis-butadiene and the LUMO (a) of ethene. The condition for a [4n+2] pericyclic reaction promoted by heat is that it must have only suprafacial components; the bond must be formed via orbital overlap on the same face of the π-system. This condition is given by the suggested interaction between the HOMO of cis-butadiene and the LUMO of ethene that are both asymmetric. The reaction is therefore allowed.
The interatomic carbon-carbon distance at the transition state is exactly 2.12A (slightly longer 2.27A for B3LYP/6-31G*). A comparison to average bond lengths shows that despite being longer than both sp3 and sp2 C-C bonds, the distance is shorter than two times the van der Waals atomic radius of carbon (3.40A). Hence, although a formal σ bond has not yet formed, a bonding interaction does exist between the carbons at the transition state.
| Bond | average length (nm)[5], [6] |
|---|---|
| C-C (sp3) | 0.153 |
| C=C (sp2) | 0.146 |
| VdW radius C | 0.170 |
| optimised TS at AM1 | 0.212 |
| optimised TS at B3LYP | 0.227 |
The vibrations corresponding to the reaction path at the transition state were visualised and exactly one imaginary frequency of -955.94cm-1 (-525.07cm-1 for B3LYP/6-31G*) was obtained. This frequency of vibration corresponds to the formation of the σ bond when following the reaction coordinate down into the product channel. As shown by the illustration below, the vibration is synchronous; the carbon atoms involved in the bond formation are brought into closer proximity by this motion and thus facilitate the essential orbital overlap. The remaining frequencies obtained by the calculation correspond to vibrations of the structure itself. They follow paths for which the transition state would be a local minimum. These paths go up the walls of the energy surface and are thus not responsible for the bond formation. The lowest frequency vibration of this kind occurs at 147.24cm-1 (135.80cm-1 for B3LYP/6-31G*), this asynchronous vibration is also illustrated below.
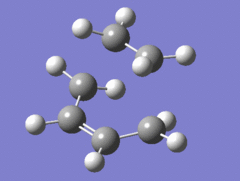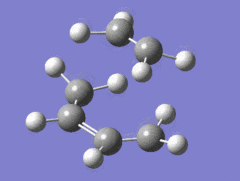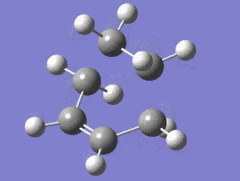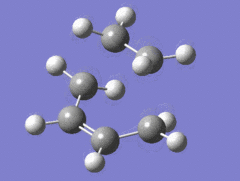 |
 |
Lastly, an IRC analysis of the transition state was run in order to verify that the proposed structure indeed leads to the expected product cyclohexene. Contrary to the Cope Rearrangement the reaction coordinate is not symmetrical and the IRC had to be run in both the forward and reverse direction. The reaction coordinate clearly indicates an exothermic reaction, the formation of the products is favourable due to the good HOMO-LUMO overlap of the reactants (LOG IRC).

Regioselectivity of the Diels-Alder reaction: Cyclohexa-1,3-diene and maleic anhydride
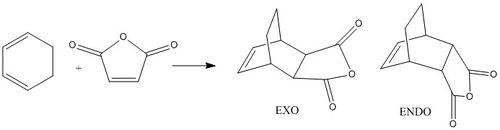
The reaction between cyclohexa-1,3-diene and maleic anhydride is an example of a Diels-Alder reaction in which stereoselective outcome is dependent on the orientation of the electron-poor dienophile during the bond formation, to yield either the exo or the endo product. According to literature the latter is formed as the major product.[7] Since the reaction proceeds under kinetic control, the endo transition state must therefore be lower in energy. This hypothesis will be tested in the following by comparing the two possible transition states based on structure, vibrational motion and MO overlap.
Optimising the reactant molecules
The endo and exo transition states were obtained by optimising the two reactant molecules individually, the corresponding frontier molecular orbitals are shown below:
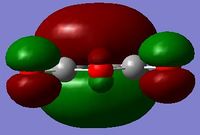
| Cyclohexa-1,3-diene (LOG) | Maleic anhydride (LOG) | |
| HOMO | 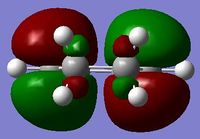 asymmetric asymmetric
|
 symmetric symmetric
|
| LUMO | 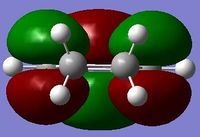 symmetric symmetric
|
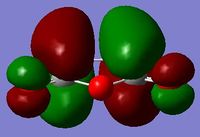 asymmetric asymmetric
|
Optimising the transition structures
The optimised structures were then arranged on top of each other in a way that the maleic anhydride olefin carbons were positioned approximately 2.2A above the centre of the cyclobutadiene. In the exo approach the carbonyl substituents on the dienophile are directed away from the electron-rich diene, whilst they are directed toward the diene in the endo approach. The guess transition state was then optimised using the Redundant coordinate editor in the frozen coordinate method at the AM1 level of theory (LOG endo, LOG exo). In the final step the resulting structure was reoptimised to the B3LYP/6-31G* level for a more accurate geometry (LOG endo, LOG exo). The latter step was found to be rather lengthy and this high level of theory would thus not be recommended for even more complex systems. The distance between the -(C=O)-O-(C=O)- fragment to the "opposite" H-atom was measured from the carbonyl carbon of maleic anhydride to the closest hydrogen atom on the diene (-CH=CH- fragment for the endo and -CHH-CH2- fragment for the exo structure).
The data clearly supports the initial hypothesis; the endo transition state is relatively lower in energy by 0.681 kcal/mol (2.56kcal/mol for B3LYP/6-31G*). The fact that this energy difference is larger for the more optimised structure suggests that the semi-empirical AM1 level does not consider all the orbital interactions and/or electron repulsions present. Still, it was confirmed that reaction proceeds under kinetic control, giving rise to the formation of endo product in excess.
A reason for this is the increased steric strain in the exo adduct, which becomes apparent in the structural features of the transition state; the distance between the -(C=O)-O-(C=O)- fragment of the approaching dienophile to the "opposite" -CH2-CH2- fragment on the diene was measured to be only 2.53A, and is hence 0.60A shorter than in the less strained endo approach. In fact, the C-H distance here is shorter than the sum of C and H van der Waals radii (2.70A), suggesting partial orbital overlap and consequently significant structural strain. The approaching maleic anhydride cannot get as close to the cyclohexadiene carbons and as a result the distance between the partially formed bonds is longer in this transition state than the corresponding distance in the endo structure.
Another important observation was that the two structures obtained for each transition state using the different levels of theory were highly similar. Differences were found primarily in the lengths of bonds formed during the reaction as the partially formed C-C bond was slightly longer for the B3LYP/6-31G* level whilst the newly formed π bond was slightly shorter. Assuming that both theories compute the transition structure at the same step along the reaction coordinate, this might be due to the higher level of theory taking a larger number of repulsive/ attractive interactions into account. Alternatively, the higher level structure could simply correspond to a transition state that occurs earlier than the one computed for AM1. Either way, the differences observed for the two levels of theory were rather insignificant. For the purpose of this exercise the semi-empirical AM1 method would have sufficed.
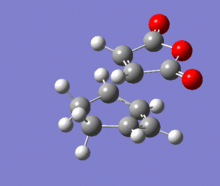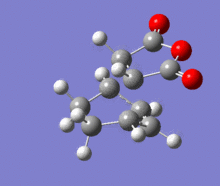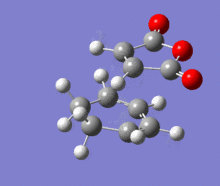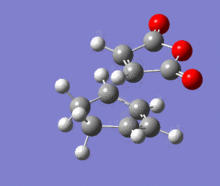
A structural representation including the relevant atomic distances (at the B3LYP/6-31G* level) is given below in addition to the corresponding vibrational animation (LOG frequ endo, LOG frequ exo).
| Endo transition state | Exo transition state | ||||||||
|---|---|---|---|---|---|---|---|---|---|
|
 |
|
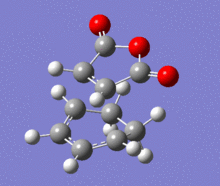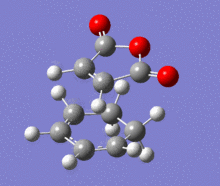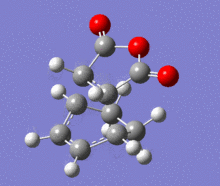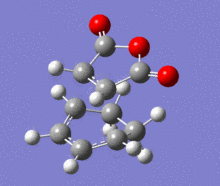 | ||||||
Each structure gave rise to exactly one imaginary frequency, hence confirming the transition state. The vibrational energy of the molecules required for bond formation in the exo approach is slightly higher. This relative difference was expected since the imaginary frequency obtained from each respective computation corresponds to the successful product formation and the energy barrier for the formation of exo product is higher.
Molecular orbital analysis
From an inspection of the molecular orbitals it follows that the antisymmetric HOMO of both the endo as well as the exo transition structure results from an interaction between the HOMO (a) of cyclohexadiene and the LUMO (a) of maleic anhydride. This observation, i.e. the diene contributes its HOMO whilst the dienophile contributes its LUMO, is identical to the one made previously for cis-butadiene and ethene. Since a flow of electrons from an electron-rich diene to an electron-poor dienophile is particularly favoured, this interaction would be expected to result in the most effective orbital overlap.
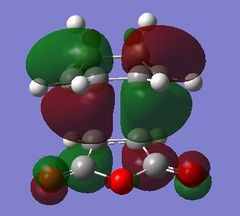
The origin of the endo selectivity proposed for this reaction can be explained using the illustration of the HOMO below. Woodward and Hoffmann proposed the so-called "secondary orbital interactions" (SOI); a stabilising interaction arising from the overlap of the carbonyl π-bond with the π-cloud on the opposite -CH=CH- fragment.[7] This stabilising effect would be relatively stronger in the endo approach as the newly formed double bond is directly above the carbonyl C=O. This is, however, not given for the exo approach where the relevant orbitals are on opposite sides of the structure. The illustrations below show the origin of this effect based on the orientation of the MOs: The electron density is further away from the carbonyl group in the exo, giving rise to more significant nodes around the -(C=O)-O-(C=O)- group. The opposite is the case for the endo structure where a significant proportion of the orbital density is getting closer to the carbonyl substituents during the approach.
 |
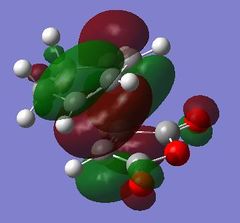 |
 |
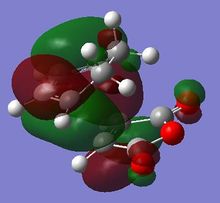 |
However, even the HOMO of the endo transition state shows no actual evidence of overlap between said orbitals. On the contrary, several nodal planes separate the -(C=O)-O-(C=O)- fragment from the rest of the structure. In fact, an analysis of the MOs obtained from the B3LYP/6-31G* basis set did not provide stronger evidence of these interactions either. In line with this observation made from a computational investigation, the theory related to "secondary orbital interactions" has caused considerable debate in the past. They were first proposed by Woodward and Hoffmann[8], but have been challenged by alternative theories in the past. Alder, for example, suggested that endo selectivity was the consequence of a plane-to-plane orientation of the diene and dienophile with "maximum accumulation of double bonds".
Moreover, the actual existence of SOI has been challenged by Garcia et al., suggesting that the existence of these interactions cannot be supported by the current state of chemical understanding.[9] This claim is based on the observation of a step-wise mechanism (as opposed to the concerted one proposed by Alder) in [6+4] and [3+4] cycloadditions as well as the relatively long through-space distance between the "interacting" orbitals (2-3A). After all, the endo selectivity observed in this computational exercise as well as in the laboratory may simply be attributed to a combination of other established interactions, such as electrostatic forces, solvent effects or steric interactions. Doubt regarding the SOI theory was supported by the fact that the MOs obtained in this experiment from using different levels of theory (AM1 vs. B3LYP/6-31G*) yielded different frontier orbitals. This renders a conclusive analysis based on Frontier Molecular Orbital Theory impossible.
References and citations
- ↑ M. J. Frisch, J. A. Pople, J. S. Binkley, J. Chem. Phys., 1984, 80, 3265. DOI:10.1063/1.447079
- ↑ R. Hoffmann, R. B. Woodward, J. Am. Chem. Soc., 1965, 87, 4389–4390. DOI:10.1021/ja00947a034
- ↑ O. Wiest, K. A. Black, K. N. Houk, J. Am. Chem. Soc., 1994, 116, 10336. DOI:10.1021/ja00101a078
- ↑ R. Hoffmann, R. B. Woodward, J. Am. Chem. Soc., 1965, 87, 2048. DOI:10.1021/ja01087a034
- ↑ F. H. Allen, O. Kennard, D. G. Watson, J. Chem. Soc., 1987, Perkin Trans. 2, S6-S8. DOI:10.1039/P298700000S1
- ↑ R. S. Rowland, R. Taylor, J. Phys. Chem., 1996, 100 (18), 7384–7391. DOI:10.1021/jp953141+
- ↑ 7.0 7.1 R. Hoffmann, R. B. Woodward, J. Am. Chem. Soc., 1965, 87, 4388–4389. DOI:10.1021/ja00947a033
- ↑ R. B. Woodward, R. Hoffmann; The Conservation of Orbital Symmetry; Academic Press: New York, 1970.
- ↑ J. I. Garcia, J. A. Mayoral, L. Salvatella, Acc. Chem. Res., 2000, 33, 658-664. DOI:10.1021/ar0000152