Rep:Mod:IJBFZ7LJRG

The Cope Rearrangement

Optimising Reactants & Products

Two guess conformers of 1,5-hexadiene were optimised - one gauche and one anti. Once optimised at the HF/3-21G level, the energies were compared with previous calculated known values.

The anti conformer (Anti2) is lower in energy than the Gauche conformer(Gauche4). Both conformers have a pair of alkyl protons loosely orthogonal to the allyl protons, and so have stabilising sigma conjugation into the π* orbitals. The anti conformer maximises the C-C σ/C-C σ* overlap, which is poorer in the gauche conformer.

Gaussian Calculation Summary
An Anti Conformer of 1,5-hexadiene(Anti2)	File Name	ANTI2OPT1
	File Type	.chk
	Calculation Type	FOPT
	Calculation Method	RHF
	Basis Set	3-21G
	Charge	0
	Spin	Singlet
	Total Energy	-231.69253530 a.u.
	RMS Gradient Norm	0.00000496 a.u.
	Imaginary Freq
	Dipole Moment	0.0001 Debye
	Point Group

The anti conformer (Anti2) is lower in energy than the Gauche conformer(Gauche4). Both conformers have a pair of alkyl protons loosely orthogonal to the allyl protons, and so have stabilising sigma conjugation into the π^* orbitals. The anti conformer maximises the C-C σ/C-C σ^* overlap, whereas these are not present in the gauche conformer.

Gaussian Calculation Summary
A Gauche Conformer of 1,5-hexadiene(Gauche4)	File Name	GAUCHE4OPT1
	File Type	.chk
	Calculation Type	FOPT
	Calculation Method	RHF
	Basis Set	3-21G
	Charge	0
	Spin	Singlet
	Total Energy	-231.69153036 a.u.
	RMS Gradient Norm	0.00000299 a.u.
	Imaginary Freq
	Dipole Moment	0.1281 Debye
	Point Group

From here, a number of other guess conformer structures were produced by altering the relative conformation of the allyl groups. Two conformers of interest (Gauche 3 & 6) both feature an allyl dihedral angle of around 60^o with varying alkene geometry. Gauche3 is the more stable than Gauche6, and also the most stable 1,5-hexadiene conformer of all. In the gauche3 conformer, the distance between the allyl groups is maximised, while still preserving the favourable C-H σ/C-H σ* and C-H σ/C-C σ* overlaps.

Gaussian Calculation Summary
A Gauche Conformer of 1,5-hexadiene(Gauche3)	File Name	ANTI3OPT1
	File Type	.chk
	Calculation Type	FOPT
	Calculation Method	RHF
	Basis Set	3-21G
	Charge	0
	Spin	Singlet
	Total Energy	-231.69266122 a.u.
	RMS Gradient Norm	0.00000449 a.u.
	Imaginary Freq
	Dipole Moment	0.3407 Debye
	Point Group	C1

Gaussian Calculation Summary
A Gauche Conformer of 1,5-hexadiene(Gauche6)	File Name	GAUCHE6XOPT1
	File Type	.chk
	Calculation Type	FOPT
	Calculation Method	RHF
	Basis Set	3-21G
	Charge	0
	Spin	Singlet
	Total Energy	-231.68961575 a.u.
	RMS Gradient Norm	0.00000449 a.u.
	Imaginary Freq
	Dipole Moment	0.4438 Debye
	Point Group	C1

Gaussian Calculation Summary
File Name	ANTI2OPT2TEST
File Type	.chk
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d)
Charge	0
Spin	Singlet
Total Energy	-234.61171035 a.u
RMS Gradient Norm	0.00000300 a.u.
Imaginary Freq
Dipole Moment	0.4438 Debye
Point Group	C1

The lowest energy anti conformer (Anti2) was then reoptimised at the B3LYP/6-31G* level. The energy at the B3LYP/6-31G* level is slightly higher, while the geometry of the molecule is minimally altered. The C=C bond lengths increase from 131.6pm to 133.3pm while the dihedral angle between allyl fragments remains at 180^o. The HĈH bond angle decreases slightly on the alkyl groups from 107.7^o to 106.7^o.

Frequency calculations were then run at both levels of optimisation and found to be in agreement with previously reported calculation

	HF/3-21G	B3LYP/6-31G*
Sum of electronic and zero-point energies (0K)	-231.539540	-234.469204
Sum of electronic and thermal energies (298.15K)	-231.532567	-234.461857

Optimizing the "Chair" and "Boat" Transition Structures

The Chair Transition Structure

The known chair transition state(TS) of the Cope rearrangement of 1,5-hexadiene was explored by first optimising a three carbon allyl fragment at the HF/3-21G level.

Gaussian Calculation Summary
An Allyl Fragment	File Name	ALLYLFRAGOPT1
	File Type	.chk
	Calculation Type	FOPT
	Calculation Method	UHF
	Basis Set	3-21G
	Charge	0
	Spin	Doublet
	Total Energy	-115.82303992 a.u.
	RMS Gradient Norm	0.00009295 a.u.
	Imaginary Freq
	Dipole Moment	0.0294 Debye
	Point Group	CS

Two of these fragments were then optimised to a transition state using two independent methods. In one the fragments were optimised to a TS using the berny algorithm, whilst in the other the system was optimised to an energy minimum having frozen the distance between the fragments.

Gaussian Calculation Summary
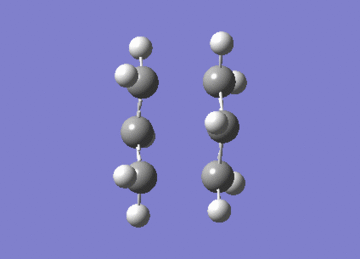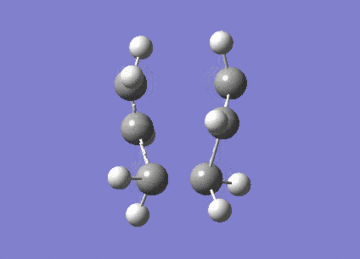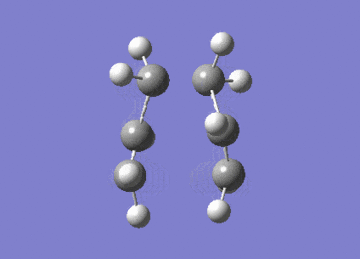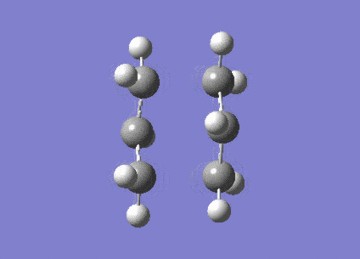Calculated Imaginary Vibration of Cope Rearrangement Chair TS	File Name	CHAIRTSOPT1ANDFREQ	CHAIRTSOPTLAS
	File Type	.chk	.chk
	Calculation Type	FREQ	FTS
	Calculation Method	RHF	RHF
	Basis Set	3-21G	3-21G
	Charge	0	0
	Spin	Singlet	Singlet
	Total Energy	-231.61932218 a.u.	-231.61932240 a.u.
	RMS Gradient Norm	0.00005635 a.u.	0.00003213 a.u.
	Imaginary Freq	1
	Dipole Moment	0.0008 Debye	0.0001
	Point Group	C1	C1

Both methods lead to the same TS as seen by the similarities in energies, and exhibit an imaginary vibration at 818cm^-1. The presence of one imaginary vibration is indicative of TSs.

The Boat Transition Structure

Geometric Data for Conformers and TS

	Anti2 conformer	Modified reactant conformer	TS
C2-C3-C4-C5 Dihedral Angle(o)	180	0	0
C2-C3-C4/C5-C4-C3 Angle(o)	111.34	100	103.39

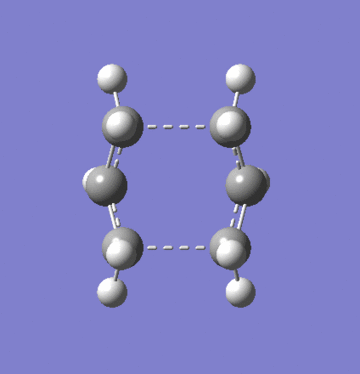
Attempts were made to generate the boat transition state using QST2 TS optimisation. QST2 optimisation requires reactant and product structures to interpolate a transition state. Using the anti2 conformation of 1,5-hexadiene, the TS could not be found. It was only when the geometry of both reactant and product were altered to more closely resemble the known TS geometry, that the boat TS was found.

Just as with the chair TS, the boat TS from the QST2 optimisation has one imaginary vibration.

Gaussian Calculation Summary
Calculated Imaginary Vibration of Cope Rearrangement Boat TS	File Name	BOAT TS QST2 FREQ
	File Type	.chk
	Calculation Type	FREQ
	Calculation Method	RHF
	Basis Set	3-21G
	Charge	0
	Spin	Singlet
	Total Energy	-231.60280249 a.u.
	RMS Gradient Norm	0.00001111 a.u.
	Imaginary Freq
	Dipole Moment	0.1584 Debye
	Point Group

From Transition States To Product

The validity of the boat and chair TSs was tested by calculating the intrinsic reaction coordinate (IRC) for each. The IRC optimises the supplied TS to it's minimum energy, generating a product associated with that energy. In the case of the Chair TS which reached a local potential energy minima in 40 steps, one IRC calculation was enough for it to generate the product - the Gauche2 conformer[1]. For the Boat TS, the IRC failed to find the local minima. In this case the calculation was run again starting with the geometry associated with the last point on the first IRC potential energy curve, with the number of points calculated increased from 50 to 75, and force constants generated for all geometries along the IRC. The second IRC calculation resulted in the energy minima correspoding to the Gauche3 conformer[2] [3].

Summary of Energetic Parameters (Hartree)

	HF/3-21G			B3LYP/6-31G*
Molecule	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.61932	-231.46670	-231.46134	-234.55698	-234.41492	-234.40900
Boat TS	-231.60280	-231.45093	-231.44529	-234.54309	-234.40233	-234.39600
Reactant (anti2)	-231.69253	-231.53954	-231.53256	-234.61171	-234.46920	-234.46185

Summary of Activation Energies (kcal/mol)

	HF/3-21G		B3LYP/6-31G*		Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.71	44.69	34.06	33.17	33.5 ± 0.5
ΔE (Boat)	55.60	54.76	41.96	41.32	44.7 ± 2.0

With both calculated transition structures in agreement with previously calculated and experimental geometries, they were optimised at the B3LYP/6-31G*[4] [5] level and frequency calculations run. These produce activation values of 34.34kcal/mol and 43.0kcal/molfor the chair and boat transition structure respectively.

The Diels Alder Cycloaddition

Prototype Reaction Of 1,3 Butadiene and Ethylene

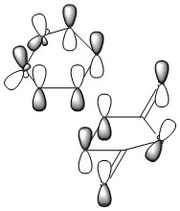
The first diels alder reaction under consideration is that of ethylene and 1,3 butadiene. The QST3 method was chosen to optimise the transition state of the reaction as the nature of the TS has been widely reported. A guess TS was built using previously reported geometric data, with an interfragment distance of 2.25Å which is consistent with reported values. Reported geometries of reactants and products were also used , and this saved on running initial semi-empirical optimisations to find a guess TS and also improved the accuracy of the optimised TS.

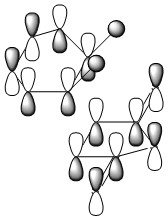
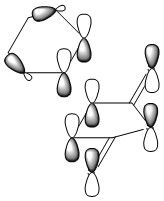
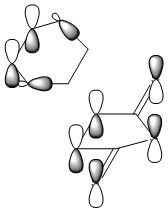
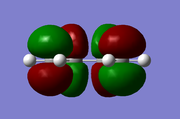
The TS was initially calculated HF/3-21G level, and its the geometry can be rationalised in terms of HOMO/LUMO interactions between 1,3 butadiene and ethylene. 1,3 butadiene has four MOs derived purely from the π system and ethylene two, as seen below;

π Electron Derived MOs

1,3 Butadiene	Ethylene
LUMO+1, s	LUMO, a
LUMO, a
HOMO, s	HOMO, s
HOMO-1, a

In a standard electron demand Diels-Alder reaction the strongest orbital overlap should be between the HOMO of the diene and the LUMO of the dieneophile. The transition state produced by the QST3 calculations also features MOs in the HOMO-LUMO region derived from other 1,3 butadiene orbitals.

The TS shows an interfragment distance of 2.2Å, significantly longer than typical C-C sp²(1.12-1.35Å) or C-C sp³(1.42-1.55Å) bond lengths. Despite this, the MOs of the HOMO/LUMO region show good overlap between the 1,3 butadiene and ethylene orbitals and this can be attributed to the relatively diffuse nature of π orbitals. Although diffuse orbitals generally lead to poorer overlap, the ethylene orbitals approach from above the plane of the 1,3 butadiene π system in forming the transition state resulting in stronger overlap and explaining the non-planar geometry of the transition state. Furthermore in the TS the fragments are much closer than they usually would prefer based purely on the Van der Waal radii of the carbon atoms (3.7Å)

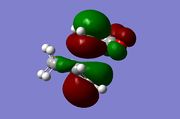
This is supported by frequency calculations at the HF/3-21G level showing an imaginary vibration corresponding to symmetric C-C bond formation (with increased bond order/length). The lowest real vibration corresponds to an asynchronous rocking between the two fragments.

Gaussian Calculation Summary
Calculated Imaginary Vibration of Diels-Alder TS	File Name	QST3 vibr input
	File Type	.chk
	Calculation Type	FREQ
	Calculation Method	RHF
	Basis Set	3-21G
	Charge	0
	Spin	Singlet
	Total Energy	-231.60320853 a.u.
	RMS Gradient Norm	0.00001111 a.u.
	Imaginary Freq	1
	Dipole Moment	0.5758 Debye
	Point Group

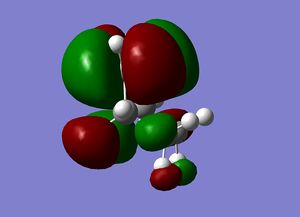
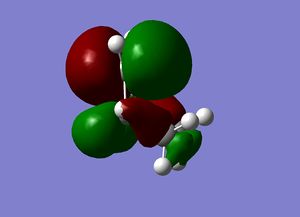
Cyclohexene MOs

LUMO+1, a

LUMO, s

HOMO, a

HOMO-1, s

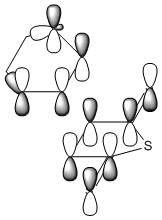
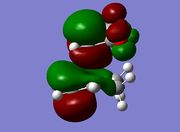
The orbitals of the HOMO-LUMO region of the calculated transition state illustrate a bonding more complex than simply π system overlap. Although the orbitals are dominated by π type interactions, the TS HOMO is an antibonding combination of a low energy antisymmetric butadiene orbital and ethylene HOMO.

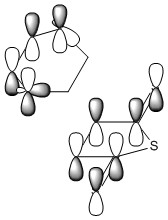
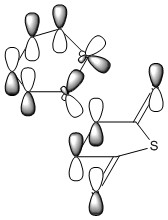
Reaction Of 1,3 Cyclohexadiene and Maelic Anhydride

The reaction between 1,3 cyclohexadiene and maelic anhydride is also suggested to occur through a concerted Diels-Alder mechanism. With the analogous reaction between cyclopentadiene and maelic anhydride being widely reported to give high endo selectivity, the reaction was also inspected using the QST3 method. The guess transition state was loosely based upon the data from the first Diels-Alder reaction studied.

Due to the more complex nature of the reactants and their interactions- namely secondary orbital overlap and steric repulsions, QST3 method was first run at AM1 level, to confirm the geometry of the TS with the guess TS. The use of semi-empirical methods has it's disadvantages and advantages. In optimising the endo-TS, calculation speed was the only real bonus to using the AM1 method and this came at the cost of accurate energy calculations. As the endo-TS is generated through maximising orbital overlap, similar theoretical transition states would also have been calculated using HF and post-HF methods. For the exo-TS however, the use of semi-empirical methods would arguably improve the acurracy of TS geometry. The exo-TS minimises steric repulsions at the expense of orbital overlap, and so electron correlation becomes an important factor in the calculation. Semi-empirical basis sets better model correlation energy than HF, resulting in a poorer improvement in TS geometry than should be expected. This is because the HF method assumes that each electron interacts with a mean field of charge with contributions from other electrons, as opposed to instantaneous electron-electron repulsions.

The TS was optimised using progressively more complex methods and larger basis sets[6] [7]. Frequency and IRC calculations were then used to confirm that the TSs are correct[8][9], with the both TSs showing one imaginary vibration. The IRC calculations were run in both forward and reverse to yield the correct product and reactant, further confirming the theoretical TS.

Summary of Diels-Alder TS Parameters

	Endo			Exo
	AM1	HF/3-21G	B3LYP/6-31G*	AM1	HF/3-21G	B3LYP/6-31G*
Electronic Energy(Hartree)	-0.05150	-605.61036	-612.68339	-0.0504	-605.60359	-612.68339
Imaginary Vibration(cm-1)	-805.35	-644.21	-446.29	-812.53	-647.44	-446.29
C-C Bond Length(Å)	2.16	2.23	2.27	2.17	2.26	2.27

In the Exo TS, the formed C-C bond length is marginally longer. The MOs for both forms are composed of the same frontier orbitals for each fragment. The HOMO-1 orbital of the endo form presents an addition orbital interaction outside of the bond forming overlap. This secondary orbital overlap between the -(C=O)-O-(C=O)- fragment and the newly formed π orbitals of the C=C bond stabilises the molecule as a whole, as in the exo form the -(C=O)-O-(C=O)- π orbitals are surrounded by orbitals of the opposite phase. The secondary orbital overlap should extend to the HOMO of the endo form as well, however is not seen due to the methods used. As previously discussed, methods with more accurate electron correlation energies will more accurately model the shape of the orbitals. Due to computational time constraints it was not viable to model the transition state using methods that would show secondary orbital overlap in the HOMO.

The exo LUMO has significantly more antibonding interactions, with a considerably larger relative energy that that of the endo LUMO. In the endo structure both the LUMO and LUMO+1 have negative relative energies, possibly indicating that the structure would be more stable with addition electrons. This could however be wrong, and simply a product of the methods and basis sets used to optimise the structure.

MOs of endo and exo product	Endo		Exo
LUMO+1, a	LCAO for LUMO+1, a	LUMO+1, a	LCAO for LUMO+1, a
LUMO, s	LCAO for LUMO, s	LUMO, s	LCAO for LUMO, s
HOMO, s	LCAO for HOMO, s	HOMO, s	LCAO for HOMO, s
HOMO-1, a	LCAO for HOMO-1, a	HOMO-1, a	LCAO for HOMO-1, a