Rep:Mod:IGE15
Revision
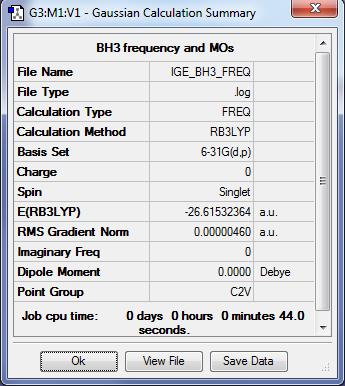
BH3
Optimisation summary
Method: RB3LYP
Basis set: 6-31G(d,p)
Item Table
Item Value Threshold Converged? Maximum Force 0.000009 0.000450 YES RMS Force 0.000006 0.000300 YES Maximum Displacement 0.000040 0.001800 YES RMS Displacement 0.000024 0.001200 YES
Low Frequencies Table
Low frequencies --- -18.4109 -13.9057 -9.0110 0.0002 0.0008 0.0008 Low frequencies --- 1162.9560 1213.1296 1213.1435
After constraint to D3h and optimisation, molecule remained C2V, demonstrator said to continue. Negative frequency not within 15cm-1 as a result.
Log file
jmol image
BH3 |
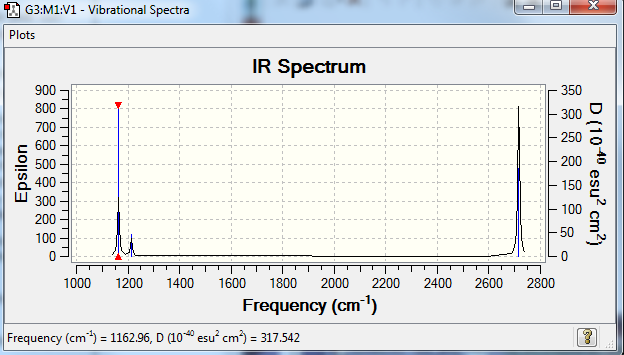
IR Spectrum
| wavenumber (cm-1 | Intensity (arbitrary units) | symmetry | IR active? | type |
| 1163 | 93 | A2ˈˈ | yes | out-of-plane bend |
| 1213 | 14 | Eˈ | yes | bend |
| 1213 | 14 | Eˈ | yes | bend |
| 2583 | 0 | A1ˈ | No | Symmetric stretch |
| 2716 | 126 | Eˈ | Yes | Asymmetric stretch |
| 2716 | 126 | Eˈ | Yes | Asymmetric stretch |
Molecule in calculation is C2V and so Gaussian calculated vibrations to be B1 A1 B2 A1 A1 B2. However correct symmetries for D3h are displayed in the above table.
To be IR active, the vibration must cause a change in dipole moment. The symmetric stretch does not cause any change in dipole moment and does not feature in the IR spectrum. Additionally, there are 2 pairs of degenerate vibrations which will each feature as a single peak. As a result, there are 3 peaks representing 3 discrete energies that arise from 5 IR active vibrations.
Smf115 (talk) 18:34, 23 May 2018 (BST)Good consideration of the symmetry shown by checking with the demonstrator and reassigning the symmetries to the correct point group. Clear explaination and correctly assigned vibrational modes.
Computed vs LCAO MO comparison
LCAO diagram for BH3 taken from tutorial problem sheet at http://www.huntresearchgroup.org.uk/teaching/teaching_comp_lab_year2a/Tut_MO_diagram_BH3.pdf, accessed on 08/05/2018.
It can be seen that the orbitals derived qualitatively using LCAO somewhat resemble the MOs calculated in Gaussian. The locations of the nodes are correctly predicted, however the orbital shapes are inaccurate and do not cover the whole molecule as the calculated MOs do.
This indicates that LCAO is sufficient to give a rough understanding of the phases of the orbital and in some simple cases such as a2ˈˈ or a1ˈ accurately predicts electron density, but cannot be relied upon to predict orbital shapes.
Smf115 (talk) 18:35, 23 May 2018 (BST)Nice inclusion of the MOs and good explaination of both the similarities and differences.
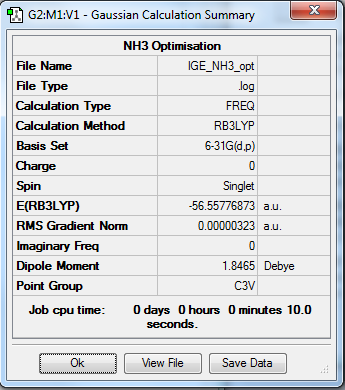
NH3
Optimisation summary
Method: RB3LYP
Basis set: 6-31G(d,p)
Item Table
Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000014 0.001800 YES RMS Displacement 0.000009 0.001200 YES
Low Frequencies Table
Low frequencies --- -0.0130 -0.0028 -0.0008 7.0749 8.0912 8.0915 Low frequencies --- 1089.3840 1693.9368 1693.9368
Log file
jmol image
NH3 |
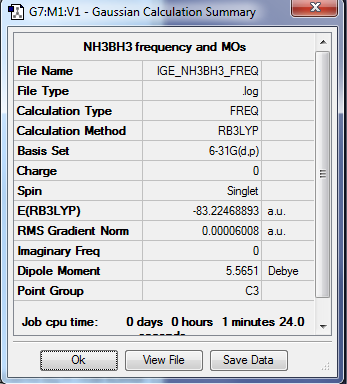
NH3BH3
Optimisation summary
Method: RB3LYP
Basis set: 6-31G(d,p)
Item Table
Item Value Threshold Converged? Maximum Force 0.000122 0.000450 YES RMS Force 0.000058 0.000300 YES Maximum Displacement 0.000541 0.001800 YES RMS Displacement 0.000298 0.001200 YES
Low Frequencies Table
Low frequencies --- -0.0250 -0.0034 -0.0012 17.1370 17.1394 37.1731 Low frequencies --- 265.7959 632.2130 639.3537
Log file
jmol image
NH3 |
Energy Calculations
E(BH3) = -26.6153 Eh
E(NH3) = -56.5578 Eh
E(NH3BH3) = -83.2246 Eh
Association Energy = E(NH3BH3)-E(BH3)-E(NH3) = -0.0515 Eh = -138 kJmol-1
This magnitude of bond strength is moderate: stronger than intermolecular bonding such as Hydrogen bonding (~20 kJmol-1), but weaker than typical covalent bonds such as C-C (~346 kJmol-1).
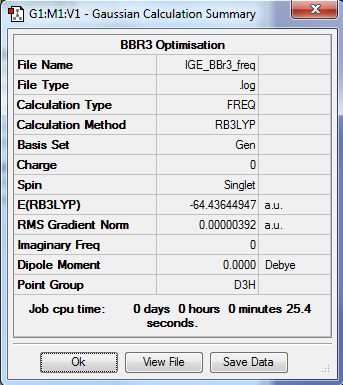
BBr3
Optimisation summary
Method: RB3LYP
Basis set: 631_g(d,p), (B), LanLDZ (Br)
Item Table
Item Value Threshold Converged? Maximum Force 0.000008 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000037 0.001800 YES RMS Displacement 0.000018 0.001200 YES
DOI
Low Frequencies Table
Low frequencies --- -2.3055 -0.0029 -0.0018 0.0774 0.7534 0.7534 Low frequencies --- 155.9402 155.9405 267.6894
Log file
jmol image
BBr3 |
Project: Aromaticity
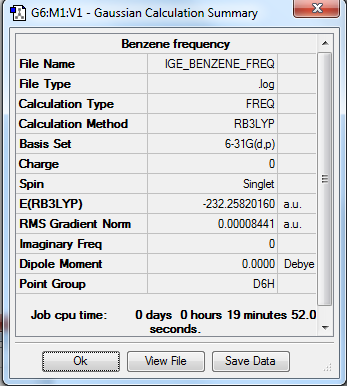
Benzene
Optimisation summary
Method: RB3LYP
Basis set: 6-31G(d,p)
Item Table
Item Value Threshold Converged? Maximum Force 0.000195 0.000450 YES RMS Force 0.000084 0.000300 YES Maximum Displacement 0.000767 0.001800 YES RMS Displacement 0.000327 0.001200 YES
Low Frequencies Table
Low frequencies --- -16.9596 -14.6538 -14.6538 -0.0056 -0.0055 -0.0007 Low frequencies --- 414.1246 414.1246 620.9394
Log file
jmol image
Benzene |
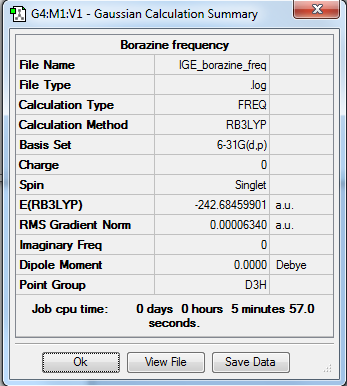
Borazine
Optimisation summary
Method: RB3LYP
Basis set: 6-31G(d,p)
Item Table
Item Value Threshold Converged? Maximum Force 0.000201 0.000450 YES RMS Force 0.000063 0.000300 YES Maximum Displacement 0.000308 0.001800 YES RMS Displacement 0.000098 0.001200 YES
Low Frequencies Table
Low frequencies --- -0.0272 -0.0123 -0.0040 3.0694 3.0949 4.1862 Low frequencies --- 289.7205 289.7212 404.4111
Log file
jmol image
Borazine |
Comparison
Charge Distribution
Carbon is slightly more electronegative than hydrogen. The result is that in benzene, every carbon has the same negative charge, -0.239. Because of the perfect symmetry of the molecule, each C-H subunit is equivalent and so every hydrogen has a positive charge of the same magnitude as carbon, 0.239. Carbon has a centre of inversion and so there is no net dipole moment.
Nitrogen is significantly more electronegative than hydrogen, while boron is slightly more electropositive than hydrogen. Depending on which atom the hydrogen is bonded to, its charge varies. In the B-H subunit, the slight electronegativity difference causes hydrogen to have a slight negative charge, -0.077. In the N-H subunit hydrogen is positively charged more so than in benzene, owing to the higher electronegativity of nitrogen versus carbon. Because the neighbouring atoms in the ring of borazine are of different electronegativity, the boron (0.747) and nitrogen (-1.103) atoms are much more charged than the carbon atoms in the ring of benzene, which are all of the same electronegativity. Each opposite pair of H-N B-H has a net dipole of 0 however and so borazine, like benzene, also has no net dipole moment, despite the loss of symmetry.
Smf115 (talk) 18:32, 23 May 2018 (BST)Great explaination of the charge distribution due to the difference in electronegativities and consideration of the dipole moment and symmetry. To improve the point groups of the molecules could be mentioned and the charge distributions should be highlighted by the same colour range across the molecules.
MOs
| Benzene MO | Borazine MO | Comments |
|
|
Benzene MO 19 (-0.33962 Eh) and borazine MO 18 (-0.31995 Eh) are examples of occupied sigma bonding orbitals with significant anti-bonding character. In both orbitals there are 4 nodal regions running across the molecule. In the borazine orbital symmetry is lost in one axis. As a result, it is a slightly higher energy. |
|
|
Benzene MO 17 (-0.35997 Eh) and borazine MO 17 (-0.36130 Eh) are occupied pi bonding orbitals with predominantly bonding character. They are extremely similar in shape and are both very delocalised. Most of the symmetry present in the benzene orbital is retained in the borazine orbital. As a result, they are very close in energy. |
|
|
Benzene MO 13 (-0.45822 Eh) and borazine MO 16 (-0.38649 Eh) are occupied sigma bonding orbitals with some antibonding character. There are 3 nodal planes running through the molecules, between each X-H subunit, leading to very localised electrons on each X-H bond. In the borazine orbital, there is a loss of symmetry as well as greater antibonding character, with the addition of nodes on each boron atom. The result of this is a much higher energy borazine orbital. |
Aromaticity Discussion
At the surface level, the shape of the pi bonding MOs in benzene and borazine show the delocalisation of electrons across multiple atoms above and below the ring.
The consideration of only pi electron in contributing to aromaticity is, however, a flawed approximation. It has been widely postulated that the sigma electron structure has an important role.[1]
In fact, it is suggested that contrary to classical thinking, pi electrons prefer to localise while sigma electrons prefer to delocalise.[2] Using this idea, the relative aromatic resonance energies of benzene and borazine can be explained.
It can be seen that in benzene there is significantly more sigma delocalisation compared with borazine, whose comparative MOs often have limited delocalisation, wherein some hydrogen atoms are not involved (MO7) and/or each lobe only includes 2 or 3 bonds (MO9). The end result of this poorer delocalisation is that benzene has a larger aromatic resonance energy than borazine. This result is more difficult to explain using only a pi orbital approach, hence why the concept of overlapping pz AOs is a poor description.
Smf115 (talk) 18:30, 23 May 2018 (BST)Excellent reference to the MOs just visualised in explaining how the overlapping pz AOs is a bad description of aromaticity. To improve, the key concepts of aromaticity could have been discussed and developed more to give a wider discussion.
Smf115 (talk) 18:30, 23 May 2018 (BST)Overall a very good report with clear understanding throughout.
Optional Comments
As always, viewing the "real" orbitals is extremely elucidating into the character of a molecule. The conclusion that sigma electrons may contribute more to aromatic resonance than pi electrons was surprising. Although I have been exposed to other ideas of aromaticity such as in 3d systems of boranes, it has always been drilled in that pi electrons are the driving force for stability ever since first learning about resonance stabilisation.