Rep:Mod:IAB
Ignacy Bartnik's Wiki Page
NH3 Molecule
Results of Gaussian calculations
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| E(RB3LYP) | -56.5577687 a.u. |
| RMS Gradient Norm | 0.00000485 a.u. |
| Point Group | C3V |
| N-H bond length | 1.02 Å |
| H-N-H bond angle | 106° |
Final results table from .log file
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986274D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
.log File of NH3 Molecule
File:IAB18 NH3 OPTIMISATION.LOG
Interactive model of NH3 Molecule
NH3 molecule |
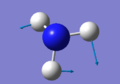
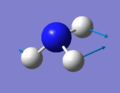
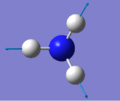
NH3 Vibrations
Screen Shot of calculated Vibrations
Calculated Vibrations of NH3
| Mode | 1 | 2 | 3 | 4 | 5 | 6 |
| wavenumber cm-1 |
1090 | 1694 | 1694 | 3461 | 3590 | 3590 |
| symmetry | A1 | E | E | A1 | E | E |
| intensity arbitrary units |
145 | 14 | 14 | 1 | 0 | 0 |
| image | 
|
|
|
|
|
|
Modes 2 and 3 are degenerated with respect to each other and modes 5 and 6 are also degenerated with respect to each other. 6 modes of vibrations would be expected of NH3 using the 3N-6 rule and indeed 6 modes were calculated. Modes 1, 2, and 3 are bending vibration modes, while modes 4, 5, and 6 and bond stretching vibration modes. Mode 4 is highly symmetric. 2 bands would be expected in an IR spectrum, corresponding to absoptions for 1 and 2 & 3. 2 & 3 would be indistinguishable as they are degenerate, vibrational mode 4 does not have a change in dipole, so it would not be visible in an IR spectrum and mode 5 & 6 have a very low intensity so they could be seen in a very delicate spectrometer but most of the time, they too would be undetectable. Vibration mode 1 is the so called umbrella motion vibration.
Charge Distribution of NH3
| Atom | N | H |
|---|---|---|
| Charge (elementary charge) | -1.125 | 0.375 |
It would be expected for the nitrogen to have a negative charge and hydrogen to have a partial positve charge as the nitrogen is more electronegative and indeed, this is also found in the calculations.
N2 Molecule
Results of Gaussian calculations
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| E(RB3LYP) | -109.5241287 a.u. |
| RMS Gradient Norm | 0.00000060 a.u. |
| Point Group | D*H |
| N-N bond length | 1.11 Å |
| N-N bond angle | 180° |
Final results table from .log file
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.401096D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
.log File of N2 Molecule
File:IAB18 N2 OPTIMISATION.LOG
Interactive model of N2 Molecule
N molecule |
N2 Vibrations
Screen Shot of calculated Vibrations
Calculated Vibrations of N2
| Mode | 1 |
| wavenumber cm-1 |
2457 |
| symmetry | SGG |
| intensity arbitrary units |
0 |
| image | 
|
For the N2 molecule, only 1 mode of vibration would be expected from the 3N-5 rule (not 3N-6 as it is a linear molecule), and indeed only 1 vibrational mode is predicted by the calculations. Since there is only one mode, there is no degeneracy possible. The one mode is a bond stretch vibration. It would not be IR active as it does not change the dipole of the molecule, so N2 would not be visible in an IR spectrum.
Charge Distribution of N2
| Atom | N |
|---|---|
| Charge (elementary charge) | 0 |
It would be expected that there is equal charge distribution over the whole N2 molecule as it is a elementary diatomic molecule, meaning it is purely covalent and both the nitrogens are identical in their electronegativity. Therefore, their electron attraction cancels each other out completely. This is also what was calculated, resulting in no charge on the individual atoms and no dipole.
H2 Molecule
Results of Gaussian calculations
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| E(RB3LYP) | -1.1785394 a.u. |
| RMS Gradient Norm | 0.00000017 a.u. |
| Point Group | D*H |
| H-H bond length | 0.74 Å |
| H-H bond angle | 180° |
Final results table from .log file
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
.log File of H2 Molecule
File:IAB18 H2 OPTIMISATION.LOG
Interactive model of H2 Molecule
H molecule |
H2 Vibrations
Screen Shot of calculated Vibrations
Calculated Vibrations of H2
| Mode | 1 |
| wavenumber cm-1 |
4466 |
| symmetry | SGG |
| intensity arbitrary units |
0 |
| image | 
|
For the H2 molecule, only 1 mode of vibration would be expected from the 3N-5 rule (not 3N-6 as it is a linear molecule), and indeed only 1 vibrational mode is predicted by the calculations. Since there is only one mode, there is no degeneracy possible. The one mode is a bond stretch vibration. It would not be IR active as it does not change the dipole of the molecule, so H2 would not be visible in an IR spectrum. In this aspect the H2 molecule is very similar to the N2 molecule.
Charge Distribution of H2
| Atom | H |
|---|---|
| Charge (elementary charge) | 0 |
It would be expected that there is equal charge distribution over the whole H2 molecule as it is a elementary diatomic molecule, meaning it is purely covalent and both the hydrogens are identical in their electronegativity. Therefore, their electron attraction cancels each other out completely. This is also what was calculated, resulting in no charge on the individual atoms and no dipole.
Bond Length of N2 in mono-metallic transition metal complex
Interactive model of MABVER Molecule |
| Complex | N-N bond length(Å) |
|---|---|
| MABVER | 1.08[1] |
The transition metal complex with N2 can be found here [1]
The bond length of the N2 in the MABVER complex is shorter than the calculated bond length of N2 . This is not expected as the N2 would donate some of its electrons from its bonding orbitals to the metal (as it has none in non-bonding orbitals), and then there would be some overlap of its non bonding orbitals and the metal electrons orbitals, so the N2 bond should be weaker resulting in a longer bond. However, this is not necessarily true, and it is possible that if the whole complex and not just N2 was calculated, the same bond length would be found. Even if it was not, this can still be explained by the fact that a simplified theory is being used to reduce compute time, and it also does not incorporate packing effects, which could well result in a shorter bond length as well.
Calculating the energy of Haber Bosch Process
| E(NH3) | 2*E(NH3) | E(N2) | E(H2) | 3*E(H2) | ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= | |
|---|---|---|---|---|---|---|
| Energy (au) | -56.5577687 | -113.1155375 | -109.5241287 | -1.1785394 | -3.5356181 | -0.0557907 |
| Energy (kJ mol -1) | -148492.4 | -296984.8 | -287555.6 | -3094.3 | -9282.8 | -146.5 |
In terms of energy, N2 is most stable, NH3 is less stable and H2 is least stable. Even though N2 is very stable, the reaction of 3H2 + N2 → 2NH3 is energetically favorable, as NH3 is also quite stable and H2 has a reltively low stability.
CN- Molecule
Results of Gaussian calculations
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| E(RB3LYP) | -92.8245315 a.u. |
| RMS Gradient Norm | 0.00000704 a.u. |
| Point Group | CinfV |
| C-N bond length | 1.18 Å |
| C-N bond angle | 180° |
Final results table from .log file
Item Value Threshold Converged?
Maximum Force 0.000012 0.000450 YES
RMS Force 0.000012 0.000300 YES
Maximum Displacement 0.000005 0.001800 YES
RMS Displacement 0.000008 0.001200 YES
Predicted change in Energy=-6.650397D-11
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1841 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
.log File of CN- Molecule
File:IAB18 CN- OPTIMISATION.LOG
Interactive model of CN- Molecule
CN- molecule |
CN- Vibrations
Screen Shot of calculated Vibrations
Calculated Vibrations of CN-
| Mode | 1 |
| wavenumber cm-1 |
2139 |
| symmetry | SG |
| intensity arbitrary units |
8 |
| image | 
|
For the CN- molecule, only 1 mode of vibration would be expected from the 3N-5 rule (not 3N-6 as it is a linear molecule), and indeed only 1 vibrational mode is predicted by the calculations. Since there is only one mode, there is no degeneracy possible. The one mode is a bond stretch vibration. Unlike the other diatomics analysed on this wiki page, the CN- would be IR active as it does change its dipole of the molecule with the vibration, as it has an overall dipole and the distance between the charges changes as it vibrates.
Charge Distribution of CN-
| Atom | C | N |
|---|---|---|
| Charge (elementary charge) | -0.246 | -0.754 |
It would be expected that there is an unequal charge distribution that is overall negative for the CN- molecule as it is a simple diatomic with a negative charge. Indeed, the calculations show that both the nitrogen and carbon have negative charges, with the nitrogen having more of the negative charge, which again agrees with expectations as nitrogen is more electronegative and more electron rich, starting in its elemental state with a lone pair.
MOs of CN-
| Arbitrary MO number | 1 | 2 | 3 | 4 | 5 |
| image | 
|
|
|
|
|
| MO number as seen in gaussian | 1 | 6 | 7 | 8 | 10 |
| Energy au |
-14.00393 | -0.01696 | 0.01857 | 0.35435 | 0.59206 |
| Occupied? | Occupied | Occupied | Occupied | Unoccupied | Unoccupied |
| Bonding? |
Bonding | Bonding | Bonding | Anti bonding | Anti bonding |
| AO contribution |
According to a traditional MO diagram, this orbital consists of 1s AOs of C and N combinding to make a σ bonding orbital, but gaussian predicts that this will be practically just the 1s nitrogen AO which is also what it displays in the image. | According to a traditional MO diagram, this orbital consists of 2p AOs of C and N combinding to make a π bonding orbital. According to the calculations,2px orbitals of both the N and C are the major contributors while the 3px also play a role. The other AOs do not play a relevant role. Both C and N contribute more or less equally. | According to a traditional MO diagram, this orbital consists of 2p AOs of C and N combinding to make a σ bonding orbital. According to the calculations, the major positively contributing AOs are the 3s orbital from the carbon and the 2pz from the nitrogen. The negative contributers are the carbon 3pz and 2pz. | According to a traditional MO diagram, this orbital consists of 2p AOs of C and N combinding to make a π* anti-bonding orbital. According to the calculations,3py orbitals of both the N and C are the major contributors while the 2py also play a role. The other AOs do not play a relevant role. Both C and N contribute equally. | According to a traditional MO diagram, this orbital consists of 2p AOs of C and N combinding to make a σ* anti-bonding orbital. According to the calculations, the nitrogen 3s orbital has a large positive contribution while the carbon 3s has an equal but negative contribution and then, the C 3pz also has a large negative contribution. This is very interesting as for the 4th MO, the traditional understanding fit very well with the calculations, while here it does not. This is probably partly due to the "traditional understanding" being referenced being quite simplistic and also, gaussian not being as reliable in calculating energetically high unoccupied MOs. |
| General comment? |
This is an orbital that is increadibly deep in energy and will therefore being practically completely inert. Nitrogen is more electronegative, so it makes sense that it will be the major contributor to the MO, although it is suprising to see just how much of the MO is due to the N and how little the C contributes. | This orbital is one level below the HOMO, so it is not as relevant for reactions, but could still concievable affect them. It is bonding and occupied, so it contributes to the bonding. It is well predicted by a traditional MO diagram, with the 2p orbitals being the largest contributing AOs. It is also degenerate with what gaussian would call MO 5, as that one is just shifted by 90° as it is made of px orbitals instead of py. | This is a very relevant orbital as it is the HOMO. It is occupied and bonding so it adds to the C-N bond. It is quite high in energy, and accessible, so it will participate in reactions whenever the molecule acts as a nucleophile. This is the orbital that will "attack" the LUMO of whatever it is reacting with. It is worthy to note that this σ orbital is higher in energy than the corresponding π orbitals, which only happens for atoms with low atomic numbers (the π/σ switch occurs for only a few compounds). | This is an unoccupied bond so it does not play a role in the bond of the molecule. However, it is the LUMO, degenerate with what gaussian labeled MO number 9, which is the other π* anti-bonding orbital. That one was not included as it is the same, just shifted 90° as it is made of px orbitals instead of py. Both of these orbitals might seem quite important, as being the LUMO, they will take part in reactions where CN- acts as an electrophile, but CN- rarely acts as an electrophile, so they are not as important. It is interesting that the 3p orbitals contribute more than the 2p orbitals. This is further evidence for it being unoccupied and being quite high in energy. | This is an unoccupied bond so it does not play a role in the bond of the molecule. Additionally, there are two other energetically lower unoccupied orbital, so it is also unlikely to take part in things lewis acid base reactions, as there the LUMO orbital will be more relevant. |
Independence Mark: CN- bond length
For my independece mark, I decided to investigate the literature value of CN- bond lengths, but because it is an ion, I decided to look at it bonded in a transition metal complex. I looked at 3 different complexes, taken from here [2] [3] [4]
Interactive model of AVARUM Molecule |
Interactive model of DEHMIP Molecule |
Interactive model of FILDEL01 Molecule |
| Complex | Average C-N bond length(Å) |
|---|---|
| AVARUM | 1.12[2] |
| DEHMIP | 1.15[3] |
| FILDEL01 | 1.14[4] |
All of these bond lengths are shorter than the 1.18 Å bond length calculated in gaussian for the ion in a vacuum. This is again, similar to what was observed for the N2 molecule. CN- and N2 are isoelectronic and have all their electrons in bonding orbitals, so when they bond to something else, like in the transition metal complexes, their bond should become weaker and therefore longer, however the opposite is observed in the examples shown above. It is impossible to tell if this is due to too many approximations in the calculation made with gaussian, or if it due to the packing effects from just this information. However, a literature value was found to be 1.14 Å [5], suggesting that it is not the packing effects that make the bond length shorted in the transition metal complexes, but that it is the gaussian calculations which wrongly predict a longer bond than is found in nature. The fact that gaussian, with the method of calculation that was used, does not meet reality exactly, should not be suprising as it is a computationally much simplified method, again, to enable performing it on a regular PC by students, and requiring hours and days of CPU time. If a different method of calculations was used, it well maybe that the correct bond length would be calculated, but then students would not be able to perform these calculations on regular PCs.
- ↑ 1.0 1.1 S.M.P.R.M.Cunha, M.F.C.G.da Silva, A.J.L.Pombeiro, Inorganic Chemistry, 2003, 42, 2157, DOI: 10.1021/ic026176e
- ↑ 2.0 2.1 Zong-xin Pi, Jian-Hong Bi, Hua-Ze Dong, Asian Journal of Chemistry, 2015, 27, 2729, DOI: 10.14233/ajchem.2015.17812
- ↑ 3.0 3.1 Maria-Gabriela Alexandru, Diana Visinescu, Sergiu Shova, Francesc Lloret, Miguel Julve, Inorganic Chemistry, 2017, 56, 12594, DOI: 10.1021/acs.inorgchem.7b02050
- ↑ 4.0 4.1 Mohammed A. Abbas, Colin D. McMillen, Julia L. Brumaghim, Inorganica Chimica Acta, 2017, 468, 308, DOI: 10.1016/j.ica.2017.07.003
- ↑ F. H. Allen, O. Kennard, D. G. Watson, L. Brammer, A. G. Orpen. Tables of bond Lengths determined by X-Ray and Neutron Diffraction. Part 1. Bond Lengths in Organic Compounds. J. Chem. Soc. Perkin Trans. II 1987, S1-S19.
Marking
Note: All grades and comments are provisional and subject to change until your grades are officially returned via blackboard. Please do not contact anyone about anything to do with the marking of this lab until you have received your grade from blackboard.
Wiki structure and presentation 1/1
Is your wiki page clear and easy to follow, with consistent formatting?
YES
Do you effectively use tables, figures and subheadings to communicate your work?
YES
NH3 1/1
Have you completed the calculation and given a link to the file?
YES
Have you included summary and item tables in your wiki?
YES
Have you included a 3d jmol file or an image of the finished structure?
YES
Have you included the bond lengths and angles asked for?
YES
Have you included the “display vibrations” table?
YES
Have you added a table to your wiki listing the wavenumber and intensity of each vibration?
YES
Did you do the optional extra of adding images of the vibrations?
YES
Have you included answers to the questions about vibrations and charges in the lab script?
YES, good explanations and sentence structure well done!
N2 and H2 0/0.5
Have you completed the calculations and included all relevant information? (summary, item table, structural information, jmol image, vibrations and charges)
YES, However you have given a bond angle of 180 for N2 and H2, there are no bond angles in diatomic molecules. Bond angles involve exactly 3 atoms.
Crystal structure comparison 0.5/0.5
Have you included a link to a structure from the CCDC that includes a coordinated N2 or H2 molecule?
YES
Have you compared your optimised bond distance to the crystal structure bond distance?
YES
Haber-Bosch reaction energy calculation 1/1
Have you correctly calculated the energies asked for? ΔE=2*E(NH3)-[E(N2)+3*E(H2)]
YES
Have you reported your answers to the correct number of decimal places?
YES
Do your energies have the correct +/- sign?
YES
Have you answered the question, Identify which is more stable the gaseous reactants or the ammonia product?
YES
Your choice of small molecule 4.5/5
Have you completed the calculation and included all relevant information?
YES, you lost the half mark for giving the bond angle - invalid for a diatomic.
Have you added information about MOs and charges on atoms?
YES, good job on the MO analysis, very detailed explanations! On MO 1 there is not much C contribution because MO 2 contains the C 1s, the AOs are too localised to interact and forming a bonding anti-bonding pair so instead you get two MOs, each with just one AO.
Independence 1/1
If you have finished everything else and have spare time in the lab you could:
Check one of your results against the literature, or
Do an extra calculation on another small molecule, or
Do some deeper analysis on your results so far
You looked up some crystal structures and analysed the different C-N bond lengths, well done!