Rep:Mod:Heg18 (01512138) IMM2 Report
NH3 Optimisation
Molecule: NH3
Calculation Method: RB3LYP
Basis Set: 6-31G(d.p)
Final Energy (a.u.): -56.5577686
RMS Gradient (a.u.):0.0005697
Point Group: C3V
Optimised H-N bond distance (Å): 1.02
Optimised H-N-H bond angle (degrees): 106
Optimisation Data
| Item | Value | Threshold | converged? |
|---|---|---|---|
| Maximum Force (N) | 0.000323 | 0.000450 | YES |
| RMS Force (N) | 0.000153 | 0.000300 | YES |
| Maximum Displacement (m) | 0.001116 | 0.001800 | YES |
| RMS Displacement (m) | 0.000922 | 0.001200 | YES |
JMol of NH3 structure
test molecule |
Analysing the Vibrations in NH3
| Mode | Wavenumber (cm-1) | Symmetry | Intensity (arbitrary units) | Image of Vibration |
|---|---|---|---|---|
| 1 | 1092 | A1 | 145 |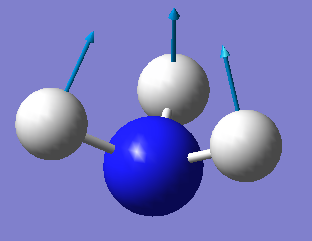 
|
| 2 | 1694 | E | 13 |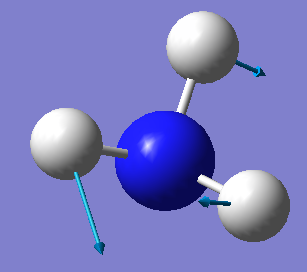 
|
| 3 | 1694 | E | 13 |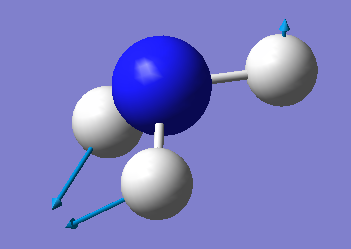 
|
| 4 | 3462 | A1 | 1 | 
|
| 5 | 3590 | E | 0.3 |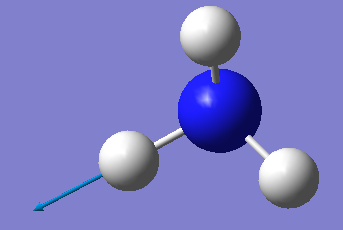 
|
| 6 | 3590 | E | 0.3 |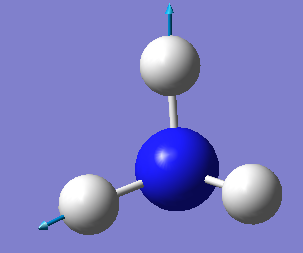 
|
How many modes do you expect from the 3N-6 rule? N=4 so you would expect 6 modes
Which modes are degenerate (ie have the same energy)? Modes 2 and 3 and modes 5 and 6 are degenerate.
Which modes are "bending" vibrations and which are "bond stretch" vibrations? Modes 1, 2 and 3 are bending vibrations whereas modes 4, 5 and 6 are stretching vibrations.
Which mode is highly symmetric? Mode 4 is highly symmetric.
One mode is known as the "umbrella" mode, which one is this? Mode 1 is the umbrella mode.
How many bands would you expect to see in an experimental spectrum of gaseous ammonia? You would expect to see 4 bands, however 2 of these bands may not be visible due the small intensity values.
NBO charges in NH3
You would expect the charge on the nitrogen atom to be negative and positive for the hydrogen atom. This is because nitrogen is more electronegative than hydrogen and therefore draws electron density towards itself. The values of the relative charge on the nitrogen and hydrogen atoms are -1.125 and 0.375 respectively.
N2 Optimisation
Molecule: N2
Calculation Method: RB3LYP
Basis Set: 6-31G(d.p)
Final Energy (a.u.): -109.5241287
RMS Gradient (a.u.): 0.0000006
Point Group: D∞H
Optimised N≡N bond distance (Å): 1.10550
Optimised N≡N bond angle (degrees): 180
Optimisation Data
| Item | Value | Threshold | converged? |
|---|---|---|---|
| Maximum Force (N) | 0.000001 | 0.000450 | YES |
| RMS Force (N) | 0.000001 | 0.000300 | YES |
| Maximum Displacement (m) | 0.000000 | 0.001800 | YES |
| RMS Displacement (m) | 0.000000 | 0.001200 | YES |
JMol of N2 structure
test molecule |
Analysing the Vibrations in N2
| Mode | Wavenumber (cm-1) | Symmetry | Intensity (arbitrary units) |
|---|---|---|---|
| 1 | 2457 | SGG | 0 |
There's no permanent dipole for N2 so the IR intensity is zero, and there will be no peak present in the spectrum.
NBO charges in N2
You would expect the charge on each nitrogen atom to be neutral with respect to each other because they are identical and the molecule has no overall charge. The relative charges of the two nitrogen atoms is 0.000.
H2 Optimisation
Molecule: H2
Calculation Method: RB3LYP
Basis Set: 6-31G(d.p)
Final Energy (a.u.): -1.1785394
RMS Gradient (a.u.):0.0000002
Point Group: D∞H
Optimised H-H bond distance (Å): 0.74279
Optimised H-H bond angle (degrees): 180
Optimisation Data
| Item | Value | Threshold | converged? |
|---|---|---|---|
| Maximum Force (N) | 0.000000 | 0.000450 | YES |
| RMS Force (N) | 0.000000 | 0.000300 | YES |
| Maximum Displacement (m) | 0.000000 | 0.001800 | YES |
| RMS Displacement (m) | 0.000001 | 0.001200 | YES |
JMol of H2 structure
test molecule |
Analysing the Vibrations in H2
| Mode | Wavenumber (cm-1) | Symmetry | Intensity (arbitrary units) |
|---|---|---|---|
| 1 | 4466 | SGG | 0.0000 |
There's no permanent dipole for H2 so the IR intensity is zero, and there will be no peak present in the spectrum.
NBO charges in H2
You would expect the charge on each hydrogen atom to be neutral with respect to each other because they are identical and the molecule has no overall charge. The relative charges of the two hydrogen atoms is 0.000.
A mono-metallic TM complex that coordinates N2
Unique Identifier: DAYSUR (mer-Chloro-dinitrogen-(methylisocyanide)-tris(trimethylphosphite)-rhenium)
N≡N bond distance (Å)= 1.120
The value of the N≡N bond distance obtained using Gaussian varied from that found in Mercury. In Gaussian the optimised bond distance for N≡N was 1.10550 Å whereas in Mercury, the value was 1.120 Å. There are a few reasons why these two results differ. Firstly, in Gaussian an optimisation process is used whereas in Mercury, the result is experimentally determined. This gives rise to differences in the state of the two molecules being measured- in Gaussian the N≡N molecule is in the gas phase, in Mercury the N≡N bond distance is measured for a solid transition metal complex. The central atom of the transition metal complex is Rhenium- some electron density is donated to the Re-N bond. This decreases the overlap of orbitals on the two nitrogen atoms, weakens the interaction and hence, lengthens the bond.
Haber-Bosch Process
E(NH3)= -56.5577686 a.u
2*E(NH3)= -113.1155372 a.u
E(N2)= -109.5241287 a.u
E(H2)= -1.1785394 a.u
3*E(H2)= -3.5356182 a.u
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.0563283 a.u
ΔE=-147.9 KJmol-1
Thermodynamically and entropically, N2 is a very stable molecule. This created problems for the production of NH3 in the Haber-Bosch process. This is solved by the use of an iron catalyst and small amounts of aluminium. The reaction occurs at high pressure, driving the reaction in favour of the formation of ammonia and high temperatures. The forwards reaction is endothermic, therefore favours lower temperatures, however a balance is necessary to ensure the rate of reaction is sufficient. [[2]].[2]
Choice of Molecule: NF3
Molecule: NF3
Calculation Method: RB3LYP
Basis Set: 6-31G(d.p)
Final Energy (a.u.): -354.0713106
RMS Gradient (a.u.): 0.00010257
Point Group: C3V
Optimised H-N bond distance (Å): 1.38404
Optimised F-N-F bond angle (degrees): 101.830
Optimisation Data
| Item | Value | Threshold | converged? |
|---|---|---|---|
| Maximum Force (N) | 0.000164 | 0.000450 | YES |
| RMS Force (N) | 0.000108 | 0.000300 | YES |
| Maximum Displacement (m) | 0.000613 | 0.001800 | YES |
| RMS Displacement (m) | 0.000296 | 0.001200 | YES |
JMol of NF3 structure
test molecule |
Analysing the Vibrations in NF3
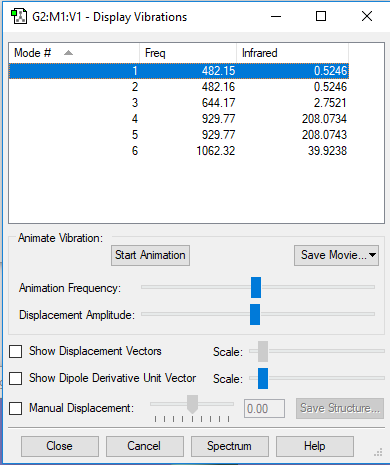
| Mode | Wavenumber (cm-1) | Symmetry | Intensity (arbitrary units) |
|---|---|---|---|
| 1 | 482 | A1 | 1 |
| 2 | 482 | E | 1 |
| 3 | 644 | E | 3 |
| 4 | 930 | A1 | 208 |
| 5 | 930 | E | 208 |
| 6 | 1062 | E | 40 |
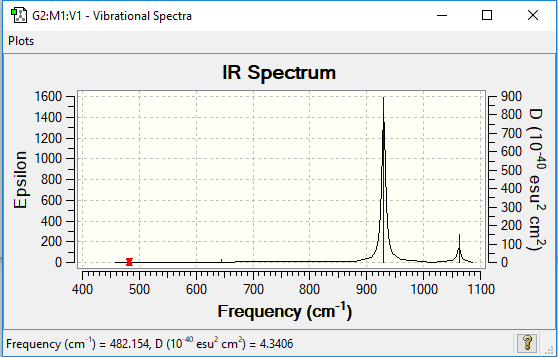
IR Spectrum of NF3
How many modes do you expect from the 3N-6 rule? N=4 so you would expect 6 modes.
Which modes are degenerate (i.e. have the same energy)? Modes 1 and 2 and modes 4 and 5 are degenerate.
The IR spectrum shows two distinct peaks, corresponding to the vibration modes 4,5 and 6. There is also small peaks at frequencies of 644cm-1 and 482cm-1 due to vibration modes 3 and modes 1 and 2 respectively.
NBO charges in NF3
You would expect the charge on the nitrogen atom to be positive and negative for the fluorine atoms. This is because fluorine atoms are more electronegative than nitrogen and therefore draw electron density towards them. The values of the relative charge on the nitrogen and fluorine atoms are -0.660 and -0.220 respectively.
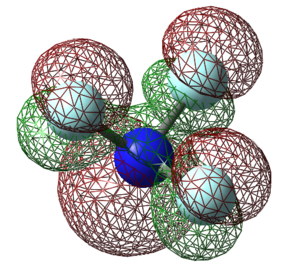
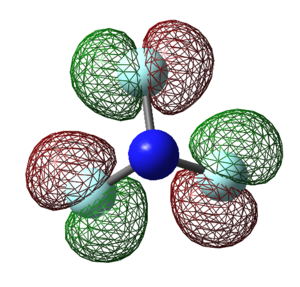
Molecular Orbitals of NF3
The molecular orbitals (MOs) for NF3 are derived from the linear combination of atomic orbitals on nearby atoms (fluorine).
| Snapshot of Molecular Orbital | Character of Molecular Orbital | |
|---|---|---|
| 1 |  |
The MO shown is the lowest unoccupied molecular orbital (LUMO) for NF3. It is a combination of bonding and anti-bonding orbitals, there is nodes along the N-F bonds. It is not very deep in energy, this is shown by the fact that large amounts of electron density can be found further from the nucleus of the central atom. The further the electron density from the nucleus, the greater the effect of shielding. This means that the electrostatic attraction between the nucleus and the electrons is reduced, and the attractive force experienced by the electrons is lessened. The energy of the MO is 0.01947 a.u. The AOs on the central atom arise from the symmetric and anti-symmetric combination of the s orbital of nitrogen with the fluorine 2p orbitals. This gives the lobes of electron density shown. |
| 2 |  |
The MO shown represents a MO that is very deep in energy, the MO is only bonding and this can be shown by the fact that there are no nodes present along the bonds. The MO is likely a combination of only s orbitals on the fluorine and nitrogen atoms. A large contribution to the MO is from the overlap of the 2s and 2s orbitals of the nitrogen and fluorine atoms. The MO shows 100% s overlap character. The MO is non-bonding since it is very deep in energy and therefore cannot provide sufficient overlap. |
| 3 |  |
The MO shown is the highest occupied molecular orbital (HOMO) for NF3. The MO has some bonding and anti-bonding character. The bonding is largely due to overlap of 2p orbitals on the nitrogen and fluorine atoms. The MO is not very deep in energy, a large amount of electron density is found at some distance from the nucleus of the central atom. It is likely that there will be no contribution of the 1s and 2s orbitals to the bonding since these orbitals are very deep in energy and cannot contribute to the bonding. The MO is a bonding orbital and electrons will be removed from this MO in order to ionise the molecule. There is likely to be some contribution of the unoccupied d orbitals. |
| 4 |  |
The MO shown here is a bonding MO, formed from the symmetric overlap of 2s and 2p orbitals on nitrogen and fluorine atoms to give bonding orbitals with some s-p mixing character. The MO will have little effect during the bonding of NF3 since it is fairly deep in energy. |
| 5 |  |
The MO shown is formed by the combination of 2px, 2py and 2pz orbitals on nitrogen and fluorine. The MO is antibonding, shown by the nodes on the N-F bonds and will not contribute to the bonding of the NF3 molecule. The MO is not very deep in energy and is occupied. The energy of the MO is -0.43590 a.u. |
Independent Work: Optimising SiH4
Molecule: SiH4
Calculation Method: RB3LYP
Basis Set: 6-31G(d.p)
Final Energy (a.u.): -291.8880276
RMS Gradient (a.u.):0.0000000
Point Group: C3V
Optimised Si-H bond distance (Å): 1.48485
Optimised H-Si-H bond angle (degrees): 109
Optimisation Data
| Item | Value | Threshold | converged? |
|---|---|---|---|
| Maximum Force (N) | 0.000000 | 0.000450 | YES |
| RMS Force (N) | 0.000000 | 0.000300 | YES |
| Maximum Displacement (m) | 0.00000 | 0.001800 | YES |
| RMS Displacement (m) | 0.000000 | 0.001200 | YES |
JMol of SiH4 structure
test molecule |
Analysing the Vibrations in SiH4
| Mode | Wavenumber (cm-1) | Symmetry | Intensity (arbitrary units) |
|---|---|---|---|
| 1 | 919 | A1 | 136 |
| 2 | 919 | E | 136 |
| 3 | 919 | E | 136 |
| 4 | 979 | A1 | 0 |
| 5 | 979 | E | 0 |
| 6 | 2244 | E | 0 |
| 7 | 2255 | E | 143 |
| 8 | 2255 | A1 | 143 |
| 9 | 2255 | E | 143 |
References
- ↑ https://www.ccdc.cam.ac.uk/structures/Search?Ccdcid=DAYSUR&DatabaseToSearch=Published (Date accessed: 01/03/19).
- ↑ https://www.chm.bris.ac.uk/~paulmay/haber.html (Date accessed: 01/03/19).
Marking
Note: All grades and comments are provisional and subject to change until your grades are officially returned via blackboard. Please do not contact anyone about anything to do with the marking of this lab until you have received your grade from blackboard.
Wiki structure and presentation 0.5/1
Is your wiki page clear and easy to follow, with consistent formatting?
YES
Do you effectively use tables, figures and subheadings to communicate your work?
YES - but you have left the captions on all the jmols as "test molecule" this is not helpful to the reader.
NH3 1/1
Have you completed the calculation and given a link to the file?
YES
Have you included summary and item tables in your wiki?
YES
Have you included a 3d jmol file or an image of the finished structure?
YES
Have you included the bond lengths and angles asked for?
YES
Have you included the “display vibrations” table?
YES
Have you added a table to your wiki listing the wavenumber and intensity of each vibration?
YES
Did you do the optional extra of adding images of the vibrations?
YES
Have you included answers to the questions about vibrations and charges in the lab script?
YES
N2 and H2 0/0.5
Have you completed the calculations and included all relevant information? (summary, item table, structural information, jmol image, vibrations and charges)
YES
However you have given a bond angle of 180 for N2 and H2, there are no bond angles in diatomic molecules. Bond angles involve exactly 3 atoms.
Crystal structure comparison 0.5/0.5
Have you included a link to a structure from the CCDC that includes a coordinated N2 or H2 molecule?
YES
Have you compared your optimised bond distance to the crystal structure bond distance?
YES - good explanation of the bonding.
Haber-Bosch reaction energy calculation 1/1
Have you correctly calculated the energies asked for? ΔE=2*E(NH3)-[E(N2)+3*E(H2)]
YES
Have you reported your answers to the correct number of decimal places?
YES
Do your energies have the correct +/- sign?
YES
Have you answered the question, Identify which is more stable the gaseous reactants or the ammonia product?
YES
Your choice of small molecule 4/5
Have you completed the calculation and included all relevant information?
YES
Have you added information about MOs and charges on atoms?
YES - good charges explanations. Some of your MO explanations are good, however some are not quite right for example MO4 is actually the antibonding counterpart to the bonding MO2.
Independence 1/1
If you have finished everything else and have spare time in the lab you could: Check one of your results against the literature, or Do an extra calculation on another small molecule, or
YES - well done!
Do some deeper analysis on your results so far