Rep:Mod:Hayley Weir Transition states and reactivity

This computational lab aims to explore the Cope Rearrangement and the Diels-Alder Reaction's potential energy surfaces. This is determined by calculating transition states structures, running IRCs and comparing activation energies. Both the Cope rearrangement and Diels Alder reaction are examples of pericyclic reactions, a class of reaction in which there is a cyclic transition state and the reaction is concerted. There are 3 main types of pericyclic reactions: electrocyclic reactions, cycloaddition and sigmatropic rearrangements.

• Electrocyclic reaction is "A molecular rearrangement that involves the formation of a σ-bond between the termini of a fully conjugated linear π-electron system (or a linear fragment of a π-electron system) and a decrease by one in the number of π-bonds, or the reverse of that process."

• A cycloaddition reaction consists of "Two or more unsaturated molecules (or parts of the same molecule) combine with the formation of a cyclic adduct in which there is a net reduction of the bond multiplicity."

• A sigmatropic rearangement is "A molecular rearrangement that involves both the creation of a new σ-bond between atoms previously not directly linked and the breaking of an existing σ-bond"

The Woodward Hoffman rules determine whether a pericyclic reaction is 'allowed'. The rule states:

In allowed thermal pericyclic reactions the number of (4q+2)_s and (4r)_a components must be odd.'

The opposite is true for photochemical reactions. This lab considers only thermally allowed reactions. 'q' and 'r' are integers, and the 's' bracket corresponds to suprafacial components and the 'a' bracket corresponds to antarafacial components.

Cope Rearrangement

The Cope rearrangement is classified as a [3,3] sigmatropic reaction. The numbers [i,j] correspond to the number of atoms between the bond breaking and bond forming in both directions of the reactions.This system is _π2_a +_π2_s + _σ2_a or _π2_s +_π2_s + _σ2_s as shown below.

Woodward Hoffman analysis of cope reaction

Diels alder WWH

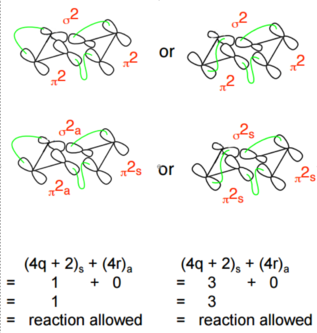
Applying Woodward Hoffman analysis to this system: _π2_s counts as 1 towards the (4q +2)_s component when q = 0 and _π2_a counts as 0 towards both components. Overall this gives (1)_s + (0)_a = 1 or (3)_s + (0)_a = 3 which are both odd, therefore this reaction is thermally allowed.

The Diels-alder reaction is classified as a [4+2] cycloaddition. The [i+j] numbering represents the number of atoms in the reacting pi systems. This system is _π4_s + _π2_s. Applying Woodward Hoffman analysis to this system: _π4_s counts as 0 towards both components as it does not satisfy either, and _π2_s counts as 1 towards the (4q +2)_s component when q = 0. Overall this gives (1)_s + (0)_a = 1 which is odd, therefore this reaction is thermally allowed.

Diels-Alder reaction mechanism

NOTE: THERE ARE LINKS TO JMOLS ON OTHER WIKI PAGES IN THIS DOCUMENT

Nf710 (talk) 16:39, 17 December 2015 (UTC)Very nic eundertsanding of the background chemistry, the reference picture is particularly good

The Cope Rearrangement Tutorial

Optimizing the Reactants and Products

Aims of section:

1. Optimize structure of anti periplanar and gauche conformers of 1,5-hexadiene
2. Determine point group of optimized structures
3. Calculate and visualize vibrational frequencies
4. Calculate potential energies to compare them with experimental values

Computational Methods

The structures in table 1 were optimized at the HF/3-21G level of theory. HF refers to Hartree-Fock and 3-21G refers the basis set. Later the 6-31G* basis set is used, which uses a higher level of theory and hence give an increased accuracy to the calculations. Hartree-Fock method uses assumptions to simplify the Schrodinger equation. Assumptions made are: total electrons in orbit around a nuclei, approximates wave functions as single electron functions (each with spacial and spin part), where the spin functions are orthonormal. These single electron wave functions can be multiplied together to form the total wave function, however the more functions, the more complicated the calculation. The Hartree-Fock method uses the minimum number of functions and so uses only a single Slater Determinant. This is a good first approximation method. More information about Hartree-Fock can be found here.

The DFT (Density Functional) method is also used in this lab. The DFT energy is given by the equation below.

E_DFT = E_NN + E_T + E_v + E_coul + E_exch+ E_corr

Where E_NN is the nuclear - nuclear repulsion energy, E_T is the kinetic energy of the electron, E_v is the nuclear - electron attraction energy, E_coul is the electron - electron Coulomb repulsion, E_exch is the electron - electron exchange energies, and E_corr is the correlated movement of electrons in different spin (not taken into account with Hartree-Fock). DFT takes into account only electron density, which the total energy is a function of, however it is unknown what this function is. Instead Local Density Approximation (LDA) or Generalized Gradient Approximation (GGA) is used.

Although DFT and Hartree-Fock are both reliable methods for describing the quantum states of many electron systems, DFT is generally preferred over the HF method. This is due to a focus in recent years of the thorough tuning of DFT to give more reliable results.

Nf710 (talk) 17:21, 17 December 2015 (UTC)Very good understanding of the methods. particularly the HF approximatations and great explanation of DFT, very impressive for a 3rd year with minimal teaching on the subject.

The reaction studied in this section is the Cope rearrangement. The reaction scheme is shown below.

Reaction scheme of the Cope rearrangement

First, several conformers of 1,5-hexadiene were optimized to determine the lowest energy conformer.

Table 1. The optimized conformer, what level of theory was used and the corresponding energy.

	Conformer	Structure	Central C-C-C-C Dihedral / o	Theory Level	Energy/ Hartrees	Point group	Comment
a)	Anti periplanar 1,5-hexadiene		-178.33742	HF/3-21G	-231.69097054	C1
b)	Gauche 1,5-hexadiene		-71.13685	HF/3-21G	-231.68961573	C1	Prediction: Higher energy than app due to steric clash. Result matched prediction.
ci)	Anti1 (Predicted lowest energy conformer)		176.87805	HF/3-21G	-231.69260231	C2	This is predicted to be the lowest energy conformer due to it being the lowest energy anti periplanar conformer in the appendix. The reason the anti periplanar conformer was expected to be the lowest energy conformer is due to consideration of steric effects in the gauche conformers that this molecule does not have.
cii)	Gauche3 (Actual lowest energy conformer)		67.69976	HF/3-21G	-231.69266116	C1	Gauche3 is the lowest conformer according to the appendix. This can be explained by looking at the HOMO, which can be seen HERE This illustrates that the two gauche pi bonds are in phase due to the 60 degree twist and so can interact to give favorable secondary orbital interactions. This lowers the energy of the HOMO, outweighing the steric effect and hence gives the lowest energy conformer.
d)	Comparision: Anit periplanar 1,5-hexadiene corresponds to anti4 in the appendix and Gauche 1,5-hexadiene corresponds to gauche5 This was deduced by comparing the energies.
e)	Anti2		179.99391	HF/3-21G	-231.69253520 cf -231.69254 from table	Ci	This structure is c i as it has a center of inversion and no other symmetry elements. The difference between this calculated energy and the energy given in appendix 1 is -4.8x10-6, and if the appendix energy is rounded then the energies are identical.

Nf710 (talk) 17:02, 17 December 2015 (UTC) This table is full of data. its good! however its a shame that on the mols of the orbitals the isovalue isnt high enough to see the secondary oritbal interaction as the orbitals are too localised. all your energies in the section are correct.

f) Reoptimization of anti2

Anti2 was run at the B3LYP/6-31G* level of theory. The B3LYP (Becke, three-parameter, Lee-Yang-Parr) exchange-correlation function is a hybrid function which comes under the DFT method and the 6-31G* basis set is of higher level of theory than the 3-21G basis set. The optimized anti2 structure at the B3LYP/6-31G* level is shown below.

A table below summarizes the comparison of anit2 at the HF/3-21G level vs B3LYP/-6-31G*of theory is shown below.

	Dihedral C=C-C-C / o	Dihedral C-C-C-C / o	Angle C=C-C /o	Angle C-C-C /o
Anti2 HF/3-21G Basis Set	114.64150	179.99391	124.80384	111.34792
Anti2 B3LYP/6-31G* Basis Set	118.58802	-179.99961	125.29922	112.67069

It can be seen from the data above that overall the geometry does not change significantly. The central C-C dihedral is negligible, however the dihedrals adjacent to the central C-C single bond vary by 4 degrees, from 114 to 118 degrees. These dihedrals are shown below.

Comparison of ethyl dihedrals from 6-31G* and 3-21G basis set calculations

The B3LYP/6-31G* method gave an energy of -234.611711664 Hartree compared to the HF/3-21G method giving an energy of -231.69253520 Hartree. These energies are significantly different, therefore it can be concluded that the 3-21G basis set gives a good approximation to the structure, however the 6-31G* basis set is needed to optimizes further and achieve the lowest and most accurate.

Nf710 (talk) 16:57, 17 December 2015 (UTC) IT IS MEANINGLESS TO COMPEAR ENERGIES! DFT and HF have completely different hamiltonians which you have just explained! you also didnt put bond lengths in but i will let you off as you have the JMOLS

g) Frequency analysis of anti2

A frequency calculation at the B3LYP/6-31G* level of theory on the optimized anti2 structure above was run. All the frequencies were positive and real, highlighting that this is a minimum structure. The frequencies and IR spectrum of the molecule are shown below.

Positive frequencies of anti2 minimum conformer

IR Spectrum of anti2 minimum conformer

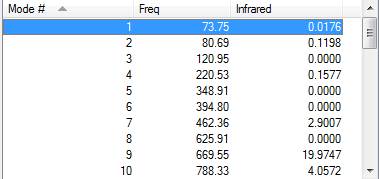
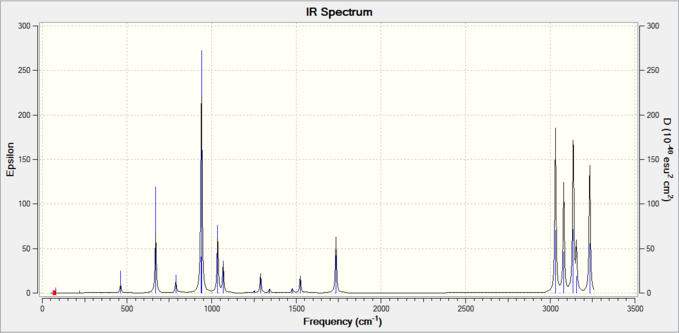
The lowest positive frequency (73.75 cm^-1) is animated below.

Task	Energy/ Hartree	Comments
(i) the sum of electronic and zero-point energies	234.469215	E = Eelec + ZPE where E is potential energy at 0 K, Eelec is electronic energy, ZPE is zero point energy
(ii) the sum of electronic and thermal energies	234.461866	E = E + Evib + Erot + Etrans where E is energy at 295 K, 1 atm and Evib, Erot,Etrans are vibrational, rotational and translational energies respectively.
(iii) the sum of electronic and thermal enthalpies	234.460922	H = E + RT Where H is enthalpy, E is energy , R is gas constant, and T is tempurature
(iv) the sum of electronic and thermal free energies	234.500800	G = H - TS Where H is Enthalpy, S is entropy, T is temperature and G is Free energy

Optimizing the "Chair" and "Boat" Transition Structures

Aims of section:

Set up a transition structure optimization of the 'chair' and 'boat' transition states by

1. Computing force constants
2. Using redundant coordinate editor and QST2 methods
3. Visualizing the Intrinsic Reaction Coordinate (IRC)
4. Calculating activation energies for Cope rearrangement for both the 'chair' and 'boat' transition state structures.
5. Determine the preferred reaction mechanism

a) Optimization of allyl fragment and guess transition state

An allyl fragment was optimized at HF/3-21G level of theory. The structure is shown below.

A Guess transition state structure was constructed consisting of two optimized allyl groups 2.2 Å apart. The point group was relaxed and then the 'symmetrize' option in Gaussview was selected to give the C_2h.

b) Optimization of chair TS

The of transition state guess structure was optimized at the HF/3-21G level and a frequency analyis was run, giving one imaginary frequency with a magnitude of -817.87 cm^-1. The optimized structure with C_2h symmetry, and the vibration corresponding to the imaginary frequency are shown below.

Chair transition state guess frequencies

This animation shows that this transition state is likely to corresponds to the formation/breaking of the single bonds from reactants to products of the cope rearrangement. This is confirmed later with an IRC.

Minimum energy structures have all positive vibrational frequencies and transition states have only one imaginary vibrational frequency.

Equation to calculate frequency

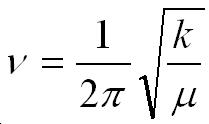
The equation above can be used to calculate the frequency according to the harmonic oscillator approximation, where v is the frequency, k is the force constant and m is the reduced mass.

Transition states are found at saddle points where all the directions leading to the saddle are positive, except one (the one the reaction coordinate will follow) as it is the second derivative of the potential energy surface. This negative gradient will therefore have a negative force constant, which will give the square root of a negative number according to the equation above which gives an imaginary number. This is why transition states give one imaginary frequency.

c) Optimization of chair TS using frozen coordinate method

The guess chair transition state was then copied into a new molecule group and one set of terminal carbons of the allyl fragments that formed/broke in the cope rearrangement where selected and the bond between them was frozen to 2.2 Å using the keyword 'opt=modredundant'. This was repeated for the other two terminal carbons. This was then optimized to a minimum at the HF/3-21G level. This is done in order to optimize the rest of the structure first to get near the transition state, and then unfreeze the bonds to get the final transition state. It is a good technique for shallow transition states or ones that are hard to find. It can be seen below that these bonds distances have remained 2.2 Å during the optimization.

d) Unfreezing bonds of chair TS and re optimizing to transition state

Now the same terminal carbons as above were selected, and instead of freezing the bond and optimizing to the structure to a minimum, the derivative was taken and the structure was optimized to a transition state as in section b. This time the force constants are not calculated as to use a normal guess Hessian modified to differentiate along the two coordinates.

A frequency analyis was run, giving one imaginary frequency with a magnitude of -817.88 cm^-1, very similar to the frequency from part b). The vibration corresponding to the imaginary frequency is shown below.

Chair transition state frequencies

Like before this animation shows that this transition state is likely to corresponds to the formation/breaking of the single bonds from reactants to products of the cope rearrangement. This is confirmed later with an IRC. A comparison of the structures from part b) and part d) are compared in the table below. Overall they are very similar.

TS structure	Distance between terminal C's of allyl groups	allyl bond angle	alyll bond length
Optimised without freezing terminal C bonds	2.02103	120.48441	1.38922
Optimised with freezing terminal C bonds	2.02071	120.52865	1.38930

e) Optimization of boat transition state using QST2 method

The QST2 method allows the reactant and product structure to be inputted into the calculation and an interpolation between them is run in an attempt to find a transition state linking the two. The structures below were inputted as the product and reactant in a QST2 calculation.

QST2 input structures with labels

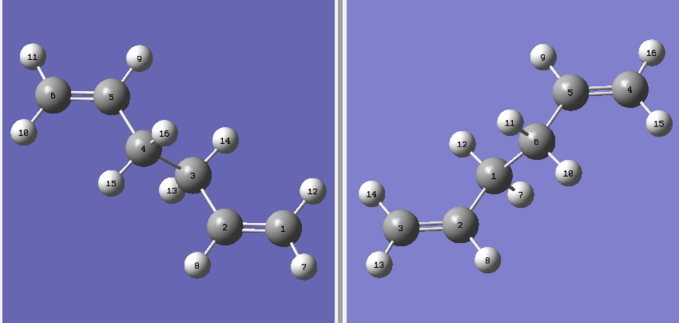
The QST2 calculation failed due to Gaussian only considering translational motion, rather than rotational and so the structure fails to reach the desired boat transition state structure.

The reactant and product structures were adjusted to look more like the boat structure. The central C-C-C-C dihedral was adjusted to 0 ^o and the central C-C-C bond angles were adjusted to 100^o. The new input structures for the QST2 are shown below.

modified QST2 input structures

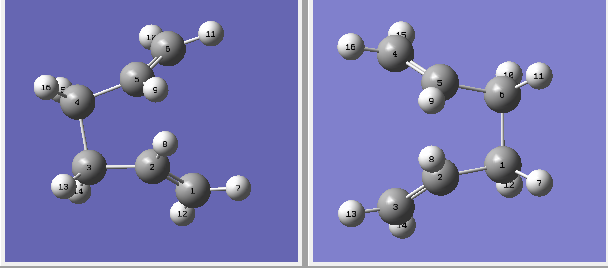
This time the interpolation gave the correct boat transition state structure, which can be seen below. This optimized boat transition state has C_2v symmetry.

A frequency calculation on this structure gave one imaginary frequency, corresponding to the formation/breaking of the terminal C-C bonds and so it is likely to be the correct transition state. An IRC is run later to confirm this.

QST2 boat transition state frequencies

Nf710 (talk) 17:06, 17 December 2015 (UTC) all your frequencies for this section are correct excellent use of jmols and great understanding of the way that a TS is derived.

f) Intrinsic Reaction Coordinate

It is hard to tell which conformers of 1,5-hexadiene the transition states correspond to from appendix 1, therefore an Intrinsic Reaction Coordinate (IRC) was run, which follows the steepest gradient of the minimum energy path to a local minimum where it stops. The IRC was only run in the forward direction only due to the energy pathway being symmetrical. An animation of the IRC and the energy level diagram is shown below.

forward IRC from Chair transition state with 50 steps

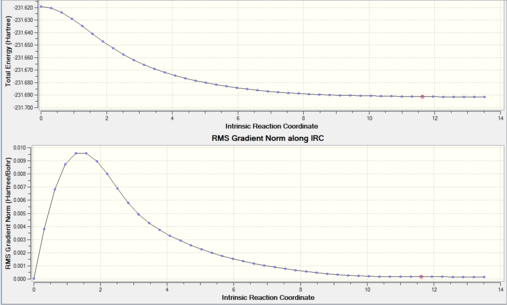
The IRC did not use all 50 steps (only 44) to complete, however the RMS gradient path does not quite reach 0 and so the final structure is not exactly the minimum. There is no point in adding more steps as not all of them have been used. Instead, since the structure was very close to a minimum, the output structure was optimized to a minimum using the HF/3-21G method. The optimization energy diagram and structure are shown below.

optimization of IRC final structure

The optimized diene had energy -231.69166702 Hartree which corresponds to the gauche2 structure from appendix 1.

Correct deduction of the confomer which connects the TS. well done

g) Calculation of Activation Energies

Structure	HF/3-21G			B3LYP/6-31G*
	Eelec/ Hartree	Eelec + ZPE/ Hartree	Eelec + Evib + Erot + Etrans/ Hartree	Eelec/ Hartree	Eelec + ZPE/ Hartree	Eelec + Evib + Erot + Etrans/ Hartree
		at 0 K	at 298 K, 1 atm		at 0 K	at 298 K, 1 atm
Chair TS	-231.61932238	-231.466705	-231.461345	-234.55698264	-234.414929	-234.409009
Boat TS	-231.60280223	-231.450930	-231.445302	-234.54309307	-234.402342	-234.396008
Reactant (anti2)	-231.69253520	-231.539540	-231.532566	-234.61171166	-234.469215	-234.461866

1 Hartree = 627.509 kcal/mol

	HF/3-21G		B3LYP/6-31G*
	at 0 K	at 298.15 K	at 0 K	at 298.15 K
ΔE (Chair)/ kcal/mol	45.70461801	44.69181849	34.06495357	33.16824321
ΔE (Boat)/ kcal/mol	55.60357249	54.75894538	41.96340936	41.32648772

In conclusion it can be seen that the cope rearrangement can proceed via a chair or boat transition state. The chair transition state has a lower activation energy than the boat transition state, illustrating that the preferred reaction pathway proceeds via the chair transition state.

Nf710 (talk) 17:14, 17 December 2015 (UTC) You have computed your energys correctly and they very closely correspond to experiment. well done. However you didn't check to see if they had imaginary frequencies or check geometries to so come to the conclusion that lower basis sets are very good at getting geoms but very bad at getting the thermodynamics correct.

Nf710 (talk) 17:14, 17 December 2015 (UTC) Beside from that this is an excellent report, one of the best I have marked, all the theory was understood to a very high level so well done.

The Diels Alder Cycloaddition

Aims of section

1. Characterize transition structures
2. Look at the shape of some of the molecular orbitals.

In this section the level of theory used for calculations was the semi-empirical AM1 (Austin Model 1) method. This method is suitable to use because it is much cheaper than B3LYP and Hartree Fock methods used before (which are purely theoretical). This is due to AM1 being heavily parameterized by using pre calculated empirical data given in the gaussian software. Since the Diels Alder reaction is a simple reaction with small molecules and only Carbon and Hydrogen atoms, the AM1 method gives reasonably accurate results so is a suitable method.

Exercise

i) Optimization of butadiene

The reaction studied in this section is the simplest Diels Alder reaction. The scheme is shown below.

Reaction shcheme of ethene + butadiene to give cyclohexadiene via cyclic transition state

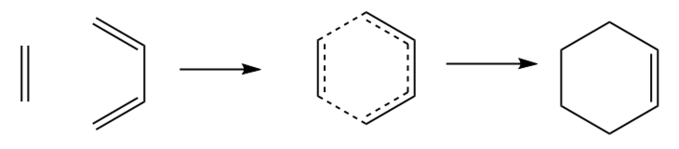
Butadiene was optimized to a minimum.

THE HOMO AND LUMO ARE SHOWN HERE.

(VERY NICE JMOLS Tam10 (talk) 17:01, 11 December 2015 (UTC))

It can be seen that the HOMO is antisymmetric and the LUMO is symmetric with respect to the plane of symmetry of the central 2 carbons.

ii) Optimization of transition state

Ethene was also optimized and the two structures where placed near each other to construct a guess transition state. An optimization of this guess structure was run. At first this calculation failed due to the molecules being too far apart (2.2 angstoms). They were placed closer together and the optimization was rerun. This time a transition state was found. The imaginary frequency is shown below with the corresponding vibration.

Imaginary frequency of Diels-Alder Transition State

To confirm that the transition state corresponds to the correct reactants and products an IRC was run. An animation of the IRC and energy diagram are shown below.

Imaginary frequency of Diels-Alder Transition State

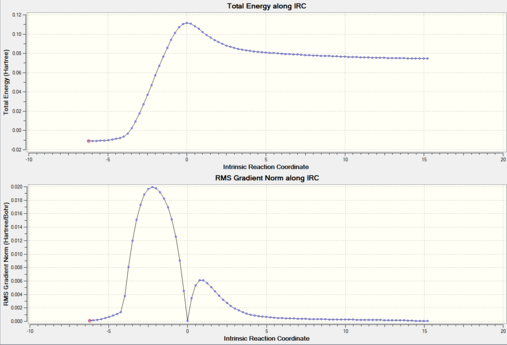Hammond postulate states that "The hypothesis that, when a transition state leading to an unstable reaction intermediate (or product) has nearly the same energy as that intermediate, the two are interconverted with only a small reorganization of molecular structure" From the IRC above it can be seen that this is a late transition state. Therefore according to Hammond postulate the energy of the transition state and hence structure is more similar to that of the products than the reactants. The HOMO and LUMO of the transition state can be seen here

iii) Studying regioselectivity of the Diels Alder Reaction

The reaction scheme studied in this section is given below.

Maleic Anhydride and Cyclohexadiene Diels Alder reaction

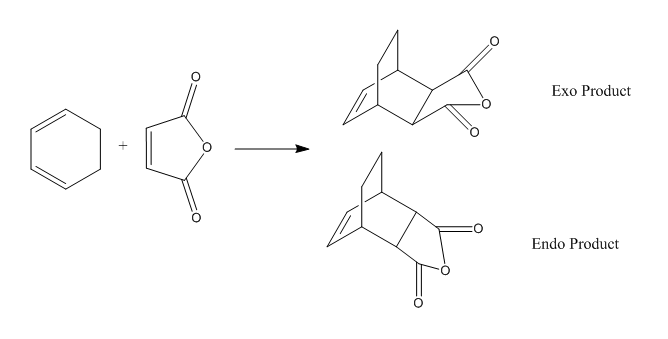
(The endo product image is a little dodgy. It makes the bonded MA carbons look sp2 hybridised. Tam10 (talk) 17:01, 11 December 2015 (UTC))

This reaction is interesting as there are two possible products: the exo product and endo product. This section will consider the regioselectivity to determine which structure is likely to be formed.

First maleic anhydride and hexadiene were both optimized individually and the optimized structures were put near to each other to produce a guess structure. These structures were then optimized to give the endo and exo minima. These minima were then adjusted slightly by lengthening the bond formed in the reaction and the structure was optimized to a transition state. Both structures have one negative frequency and the IRC running in both directions proceeds directly to the desired reactants and products. The structures of both transition states and products as well as animations of the imaginary frequency vibrations and IRCs given in the table on the link below.

THE ENDO AND EXO STRUCTURES ARE SUMMARIZED IN A TABLE HERE]

Structure
	Eelec/ Hartree	Eelec + ZPE/ Hartree	Eelec + Evib + Erot + Etrans/ Hartree
		at 0 K	at 298 K, 1 atm
Endo TS	-0.05150475	0.133494	0.133494
Exo TS	-0.05041982	0.134882	0.144883
Reactants	-0.09411295	0.089157	0.099535
Exo Products	-0.15990938	0.031701	0.040680
Endo Products	-0.16017078	0.031463	0.040461

1 Hartree = 627.509 kcal/mol

	ΔE/ kcal/mol
	at 0 K	at 298.15 K
Endo activation energy	27.82186653	27.70957813
Exo activation energy	28.69284903	28.45627813
Endo Reaction energy	-36.20350425	-37.06946667
Exo Reaction energy	-36.0541571	-36.9320422

From the data in the table it can be seen that the endo transition state is more stable that the exo transition state.

Both the endo and exo transition states HOMOs are antisymmetric. THE HOMO FOR THE ENDO AND EXO TRANSITION STATES CAN BE FOUND HERE

This can be used to explain why the endo transition state is more stable. It can be seen that the HOMO of the endo transition state's C=O bond and C=C bond from the hexadiene's pi bonds orientated so they can interact, and so secondary orbital overlap effect is excepted. This interaction cannot be seen in the exo HOMO as the oxygen is on the other side of the molecule. Looking closely at the endo transition state HOMO however, it can be seen that there is a node between the two orbitals and so secondary orbital interactions cannot occur . With this in mind it is hard to understand why the endo transition state is slightly lower in energy that the exo transition state. A possible explanation for this is the weak through space bonding between a small amount of pi bond orbitals that are in phase due to the slight twist of the molecule.

(This is fair enough. Perhaps it makes more sense looking at the reactants individually. Tam10 (talk) 17:01, 11 December 2015 (UTC))

Interestingly, the calculations show that both the endo transition state and product structure are lower in energy than the corresponding exo conformers. This implies that the endo conformer is the kinetic and thermodynamic product. However, literature agrees that the endo product is the kinetic product but states that the exo product is the thermodynamic product. This could be due to using the semi empirical method for calculations which give unreliable results.

(I'd agree more with the statement that endo is lower in energy for both the TS and product. The reference you have is talking about cyclopentadiene Tam10 (talk) 17:01, 11 December 2015 (UTC))

A summary of the bond lengths of the endo and exo transition states are shown below.

Atoms Endo TS	Bond Lengths/ Å
C3-C5	1.39724	Endo TS numbered
C5-C7	1.39305
C7-C9	1.49054
C9-C12	1.52297
C12-C1	1.49052
C1-C3	1.39305
C15-C17	1.40849
C17-C20	1.48923
C20-O23	1.40896
O23-C19	1.40896
C19-C15	1.48923

Atoms Exo TS	Bond Lengths/ Å
C3-C5	1.39677	Exo TS numbered
C5-C7	1.39439
C7-C9	1.48972
C9-C12	1.52208
C12-C1	1.48975
C1-C3	1.39437
C15-C17	1.41009
C17-C20	1.48818
C20-O23	1.40964
O23-C19	1.40962
C19-C15	1.48820

(The through-space distances between the -C(=O)-O-C(=O)- and CHD are quite important here. You need to talk about the steric effects and how they could affect the TS energies Tam10 (talk) 17:01, 11 December 2015 (UTC))

Discussion

cis butadiene

The HOMO and LUMO for cis butadiene are shown below. The HOMO is antisymmetric and the LUMO is symmetric with respect to the plane.

THE HOMO AND LUMO ARE SHOWN HERE.

ethylene + cis butadiene transition structure

The HOMO and LUMO for the ethylene + cis butadiene transition structure are shown below. The HOMO is symmetric with respect to the plane, and the LUMO is antisymmetric with respect to the central 2 carbons

THE HOMO AND LUMO OF THE ETHYLENE, CIS BUTADIENE TRANSITION STATE CAN BE SEEN HERE

The geometry of the transition structure is shown below. It can be seen that the C-C bond breaking/making distance is 0.212 Å.

|

Typical sp3 and sp2 C-C bond lengths are 154 pm and 134 pm, respectively and the Van der Waals radius of the Carbon atom is 170 pm. It can therefore be concluded that the C-C bonds highlighted above are clearly shorter than 2x the van der waals radius (340 pm) but shorter than both C-C bond lengths. This shows that there is some interaction between the Carbon atoms, as can be seen by looking at the HOMO.

The vibration of the imaginary frequency, which corresponds to the making/breaking of the C-C bond and the lowest positive frequency vibration are shown below.

Frequencies of diels alder transition state

The formation of the two new bond is synchronous. In comparison the first positive frequency does not show the formation/brekaing of the new C-C bonds.

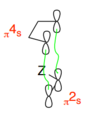
The MO's of butadiene and ethylene that have been used to form the HOMO are 3 pi orbitals of the C=C bonds on the hexadiene and the ethene. The HOMO as the transition structure is s as both the pi bonds are suprafacial. Applying woodward Hoffman analysis: _π4_s and _π2_s gives (1)_s + (0)_a = 1 which is odd, therefore this reaction is thermally allowed.

(Not quite. The MOs are delocalised across the system whereas you're talking about the bonds involved in the reaction. The MOs that make up the TS HOMO are the HOMO of butadiene (anti-symmetric) and LUMO of ethene (anti-symmetric) Tam10 (talk) 17:01, 11 December 2015 (UTC))

cyclohexa-1,3-diene reaction with maleic anhydride

The energies of the exo and endo transition states are -0.05041982 and -0.05150475, respectively. A sketch of the endo and exo transition states is shwon below.

Comparison of the endo and exo transition states

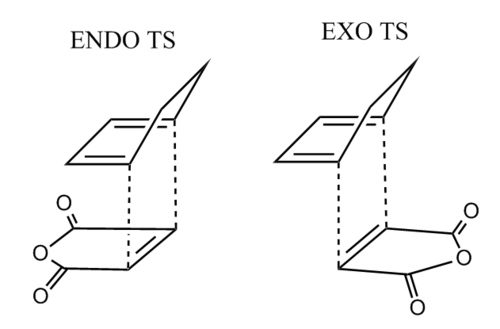
It can be seen from this diagram that the endo transition structure is able to experience secondary orbital interaction between the C=O pi bonds of the maleic anhydride and the C=C pi bonds of the hexadiene. The experimental results are discussed in the section above.

Further Discussion

The AM1 Semiempirical Method was used in this section. This is not as accurate as Hartree Fock methods used previously, as two-electron and one-electron integrals are neglected and empirical parameters are used instead. This has the plus of make the calculations cheaper however the accuracy is reduced. The error in ΔH_f for AM1 si 5.7 kcal/mol

(How does this ΔH_f compare to the other methods you're using? Tam10 (talk) 17:03, 11 December 2015 (UTC))

Conclusion

This lab has explored the potential energy surfaces of the cope rearrangement and the Diels Alder reaction. First the ground state structures of 1,5-butadiene were explored using HF/3-21G and B3LYP 6/31-G* to find the product/reactant of the cope rearrangement. It was determined that the gauche3 structure was the lowest energy conformer due to secondary orbital overlap lowering the energy of the HOMO. Next the boat and chair transition states were optimized and compared. The chair structure was optimized both directly from a guess and by freezing the C-C breaking/making bond length, and the boat transition state structure was calculated using the QST2 method. Both chair and boat optimized structures gave one negative frequency corresponding to the making/breaking of the C-C bonds, proving their transition state nature and forward IRCs were run to confirm that they were the correct structures and identify the exact reactant/product conformer. The chair structure has a lower activation energy than the boat structure and so it was concluded that the reaction proceeded via this transition state.

The second reaction studied was the Diels Alder reaction using the AM1 semi empirical method. First the reaction of ethene and butadiene was studied and the transition state was located along and an IRC frequency calculation confirmed that this was indeed the desired transition state. Finally the regioselectivity of the Diels Alder reaction was studied via the reaction between maleic anhydride and cyclohexadiene. Here two products were possible: the exo product and endo product. There was expected to be secondary orbital overlap between the C=O and C=C pi orbitals, however due to a node between the orbitals, there was a very minor interaction and so the HOMO was not significantly lowed in energy. It was also observed that the exo product was the thermodynamic product, despite the endo product being kinetically favored.

An improvement to this lab could be to repeat the calculations at the B3LYP/6-31G* level of theory to gain a higher level of accuracy. An extension could be to investigate the oxy-cope reaction to determine if it also proceeds via the chair transition state and if the gauche conformer is still the lowest in energy.