Rep:Mod:HarryAllingham
Introduction
The energy of a system can be shown by a Potential Energy Surface (PES). On a PES there is a minima and a maxima, also known as stationary points. At the minima the second derivative will be positive, while the second derivative will be negative for a maxima. The minima indicates a position where the chemical species present are stable. In the case of the exercises seen latter these chemical species are the reactants, such as butadiene and cyclohexadiene. The maxima is where the transition state is located and will occur when the energy of a reaction is at its highest.
In the three exercises, the reactants, transition states and products were all optimised at the PM6 level, while IRC analysis was used in all of the exercises to illustrate the reaction coordinate. The frequency of the reactants, transition states and products were also calculated. In exercise two, the transitions states of the endo and exo products were also found at the B3LYP/6-31G(d) level. The indication that the transition state had been found was a single negative imaginary frequency. For the reactants and products no imaginary frequencies are found.
Nf710 (talk) 16:37, 10 February 2017 (UTC) Nice brief intro, A TS has positive curvature in all co-ordinates apart from the reaction co ordinate.
Exercise 1: Reaction of Butadiene and Ethylene

MO Diagram
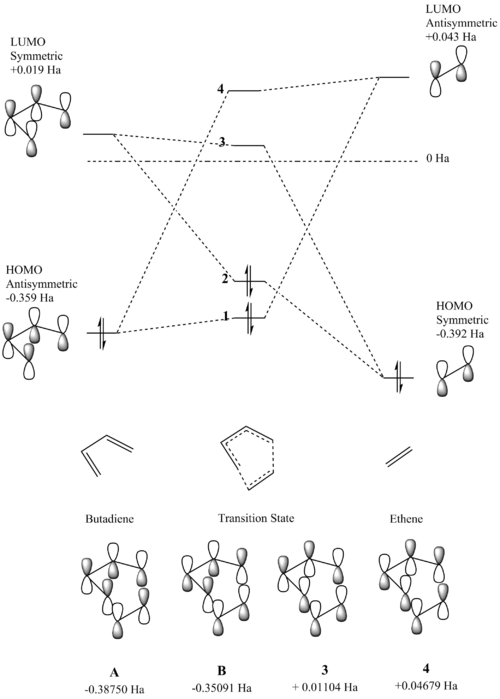
HOMOs and LUMOs
| HOMO (MO 11) | LUMO (MO 12) |

|

|
Media:BUTADIENE_OPT+FREQ_HDA14.LOG
| HOMO (MO 6) | LUMO (MO 7) |

|
|
Media:ETHENE_OPT+FREQ_HDA14.LOG
| MO 16 | HOMO (MO 17) | LUMO (MO 18) | MO 19 |
|
|
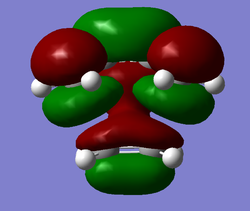
|

|
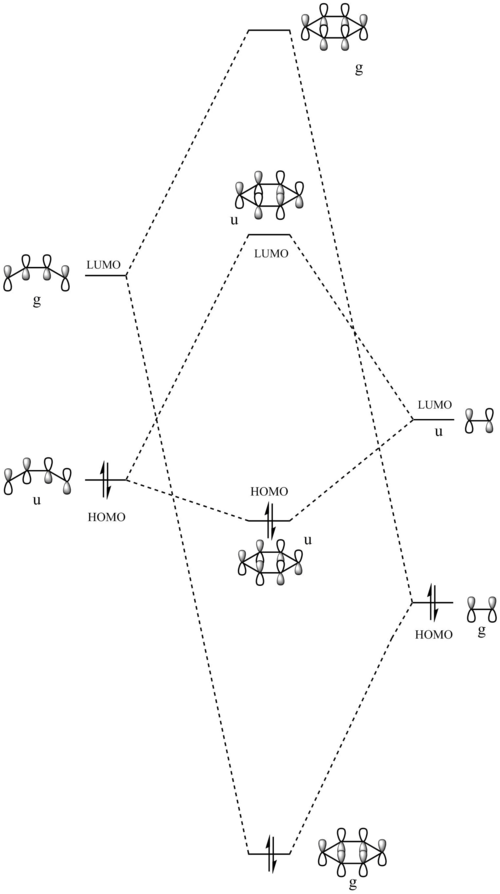
For the Diels-Alder reaction to take place a gerade orbital must be combined with another gerade orbital, while an ungerade orbital must be combined with another ungerade orbital. This is confirmed by the molecular orbitals produced for this reaction. It is known that the HOMO of the diene interacts with the LUMO of the dienophile, while the HOMO of the dienophile interacts with the LUMO of the diene. In the case of this reaction the HOMO of the diene (MO 11) is ungerade and this interacts with the ungerade LUMO of the dienophile (MO 7) resulting in the formation of an ungerade bonding orbital and an ungerade antibonding orbital, while the LUMO of the diene (MO 12) is gerade and this interacts with the gerade HOMO of the dienophile (MO 6) resulting in the formation of a gerade HOMO bonding orbital and a gerade LUMO antibonding orbital.
The overlap of the diene HOMO and dienophile LUMO will result in the orbital overlap integral being non-zero. This is because both these orbitals are ungerade. The overlap of the diene LUMO and dienophile HOMO will also result in a non-zero orbital overlap integral. This is because both orbitals are gerade. It can therefore be concluded that for the orbital overlap integral to be non-zero, the two sets of atomic orbitals combined must be of the same symmetry.
Nf710 (talk) 16:43, 10 February 2017 (UTC) Not strictly u and g as this would suggest a center of inversion which it doesnt have.
Carbon-Carbon Bond Lengths
| Carbon-Carbon Bonds | Bond Lengths (Å) | ||
|---|---|---|---|
| Reactants | Transition State | Product | |
| C1-C2 | 1.33532 | 1.37974 | 1.50034 |
| C2-C3 | 1.46838 | 1.41111 | 1.33766 |
| C3-C4 | 1.33532 | 1.37976 | 1.50034 |
| C4-C5 | 2.11458 | 1.54003 | |
| C5-C6 | 1.32732 | 1.38174 | 1.54075 |
| C6-C1 | 2.11488 | 1.54003 | |
The table shows that the carbon-carbon bond lengths C1-C2, C3-C4 and C5-C6 all increase. The bond length C5-C6 increases more than C1-C2 and C3-C4 because both carbons in the C5-C6 bond become sp3 hybridised, whereas as only C1 and C4 in the C1-C2 and C3-C4 bonds become sp3 hybridised because a new double bond forms between C2-C3. The new bonds formed, C4-C5 and C6-C1, are the same length as C5-C6 because all the carbons are sp3 hybridised.
The literature value for an sp3 hybridised carbon-carbon single bond is 1.550 Å, while the for an sp2 hybridised carbon-carbon double bond is 1.335 Å. [1] These values are very similar to the ones shown in the table above, showing that the calculations performed were accurate.
The Van der Waals radius of a carbon atom, according to Pauling (1939) is 1.70 Å [2]. This is compared to the distance of the partially formed carbon-carbon single bonds, which both had distances of 1.54003 Å. Therefore the carbons atoms that are becoming bonded are within the required distance to react.
Transition State Vibration
The transition state vibration corresponds to the imaginary frequency which comes from the second derivative of the degree of freedom. This therefore corresponds to the reaction coordinate.
Reaction Coordinate
(One issue with not choosing unique names when uploading files into a public namespace is overwriting other people's files. This example is even worse as you have forgotten to upload the image at all and have linked someone else's image! Tam10 (talk) 14:10, 27 January 2017 (UTC))
The IRC analysis of the Diels-Alder Reaction illustrates the reaction pathway that this Diels-Alder reaction takes. It shows the lengthening of carbon-carbon bonds C1-C2, C3-C4 and C4-C5, due to carbons moving from sp2 to sp3 hybridised, and the shortening of the C2-C3 bond shortly before it shows the synchronous forming of the carbon-carbon bonds C4-C5 and C6-C1 as a result of the [4+2]-Cycloaddition.
Nf710 (talk) 16:45, 10 February 2017 (UTC) Good first section. What was the electron demand of the reaction?
Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole
Molecular Orbitals
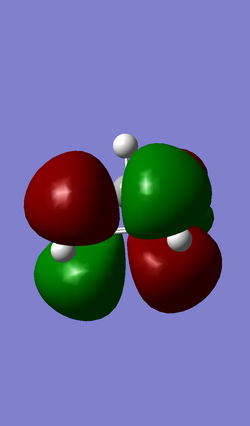
| HOMO (MO 22) | LUMO (MO 23) |
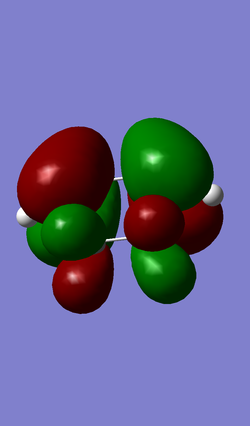
|
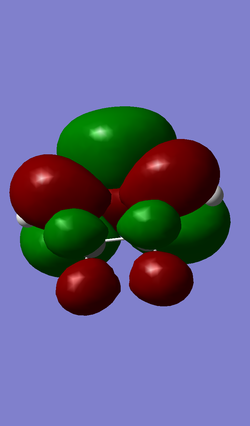
|
(Easier to see what's going on if you use transparent/mesh-type orbitals. For the casual reader, they wouldn't be able to see what atoms are where Tam10 (talk) 12:15, 7 February 2017 (UTC))
Media:CYCLOHEXADIENE_B3LYP_HDA14.LOG
| HOMO (MO 19) | LUMO (MO 20) |

|
|
| MO 40 | HOMO (MO 41) | LUMO (MO 42) | MO 43 |
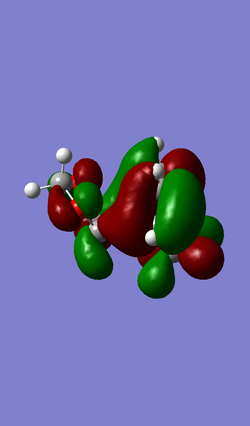
|

|
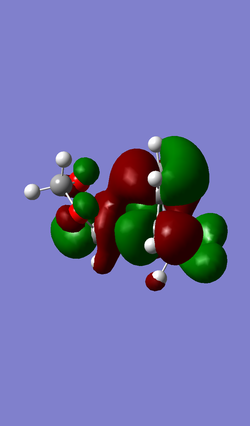
|

|
| MO 40 | HOMO (MO 41) | LUMO (MO 42) | MO 43 |

|
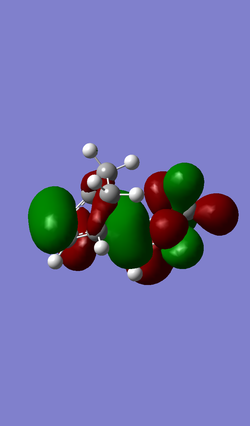
|
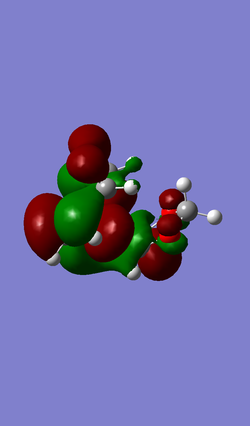
|
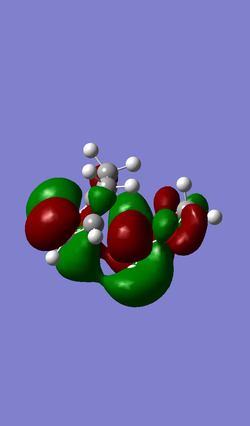
|
MO Diagram
An inverse Diels-Alder reaction is one that takes place with an electron-poor diene and an electron-rich dienophile. In the case of this reaction between cyclohexadiene and 1,3-dioxole, the diene, 1,3-dioxole, is very electron rich due to the electron donating effect of the two oxygens, which has two sets of lone pairs each. This results LUMO of the dienophile having a more similar energy to the HOMO of the diene, compared to a standard Diels-Alder, as seen in Exercise 1, where they are further apart in energy.
(Adding EDGs to the dieneophile will raise its energy, not lower it. Above, you have antisymmetric HOMO and LUMO. Below they are symmetric. You have also used the wrong symmetry labels "u" and "g", which require a centre of inversion. We ask for "a" and "s" Tam10 (talk) 12:15, 7 February 2017 (UTC))
Atomic and Molecular Orbitals have been simplified to represent the key interacting orbitals.
Thermochemistry
| Diels-Alder Product | Reactants | Transition State | Product | Activation Energy (kJ/mol) | Gibbs Free Energy (kJ/mol) |
| Exo | -1313772 | -1313614 | -1313846 | 157.5221 | 73.9262 |
| Endo | -1313772 | -1313622 | -1313849 | 149.6903 | 77.52051 |
The thermochemical data shows that the endo product will be the thermodynamic product since this reactions has the largest change in Gibbs Free Energy meaning that the product will be lower in energy. This in turn means that the exo product will be the kinetic product.
The activation energy for the formation of the endo product is lower than for the exo product because the oxygen p-orbitals of the 1,3-dioxole are able to overlap with the p-orbitals of the newly formed carbon-carbon double bond, thus stabilising the transition state. Due to the conformation of the exo product, this overlap, and so stabilisation, can not take place.
Nf710 (talk) 17:15, 10 February 2017 (UTC) You got the right answer for the reaction. which shows that the endo is both the thermo and kenetic, but you have not said this. You could have backed up these conclusions with the SOO and the sterics. But well done on getting the correct answer. not many people do.
Exercise 3: Diels-Alder vs. Cheletropic

Diels-Alder Reaction: Exo Product
Reaction Coordinate
Media:IRC_Exercise_3_exo_HDA14.LOG
IRC Analysis
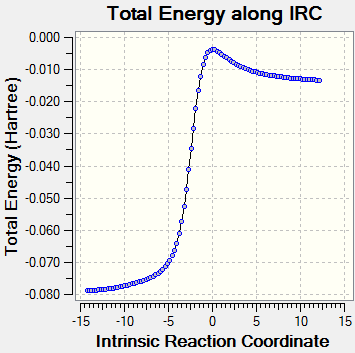
Reaction Profile

(How were these energies calculated? What did you use for reactants? Tam10 (talk) 12:15, 7 February 2017 (UTC))
The reaction profile has been normalised with respect to the reactants.
Diels-Alder Reaction: Endo Product
Reaction Coordinate
Media:IRC_Exercise_3_endo_HDA14.LOG
IRC Analysis
The two reaction coordinates for the exo and endo Diels-Alder reactions show the formation of the second 6-membered ring. The bonds between carbon and sulfur and carbon and oxygen are formed asynchronously. However the main thing to notice is that as the reaction coordinates proceed the bonding in xylylene becomes delocalised for a short period of time.
Reaction Profile

The reaction profile has been normalised with respect to the reactants.
Cheletropic Reaction
Reaction Coordinate

The Cheletropic reaction coordinate shows the formation of the 5-membered ring, instead of the 6-membered ring as seen in the Diels-Alder reactions. The two carbon-sulfur bonds are also formed synchronously, unlike in the Diels-Alder reaction where the carbon-sulfur and carbon-oxygen bonds are formed asynchronously. Once again the bonding in xylylene becomes delocalised for a small period of time, like in both the Diels-Alder reactions.
IRC Analysis
Reaction Profile

(These profiles should all be on the same diagram to allow comparison Tam10 (talk) 12:15, 7 February 2017 (UTC))
The reaction profile has been normalised with respect to the reactants.
The reactions profiles show that the Cheletropic reaction has the largest Gibbs Free Energy. This means that the product formed as a result of this reaction will be the thermodynamic product. This therefore implies that the kinetic product is the one formed as a result of the Diels-Alder reaction. The Cheletropic reactions, however, proceeds via a higher activation energy than both the exo and enod Diels-Alder product. This will be down to the higher strain associated with a 5-membered ring compared to a 6-membered ring. The endo product also has a lower activation energy than the exo, albeit only slightly. This implies that when this reaction is under kinetic control the endo product is likely to be the major product.
Conclusion
For all three exercises the reactants, transition states and products were successfully optimised at PM6 level along with frequency and IRC analysis. Exercise two also saw the successful optimisation of the reactants, transition states and products at the B3LYP/6-31G(d) level. Once again frequency and IRC analysis was performed. From these calculations, in exercise one and two, the important molecular orbitals were determined thus allowing for the construction of two MO diagrams. These calculations, for exercises two and three, allowed for the analysis of the thermochemical data. As a result major/minor and thermodynamic/kinetic products could be determined by evaluating the Activation Energies and Gibbs Free Energies of these reactions.
