Mod: Physical

Introduction

In the following exercises the Cope Rearrangement and the Diels Alder Reactions are investigated and their relative transition states are characterised. The exercise and the further examples are then explored using computational methods. Due to the fact that in many of the reactions investigated bonds are both made and broken the computational methods utilised are slightly different for those used in prior exercises. This is also maintained for the size of the molecules, as slightly larger and complex molecules are investigated. In particular molecular orbital based theory will be utilised in order to solve Schrödinger's equation numerically. The shape of the multi-dimensional potential energy surface will help to locate the various transition states. Methods such as the Hartree Fock method were an initial estimate of the wave function is made from a collection of molecular orbitals. The estimates accuracy is progressively improved with the increasing number of iterations, of the energies gradient. Another computational method utilised will be the DFT, density functional theory, where the ground state electron density is the one that is primarily focused on to provide the necessary information regarding the wave function. DFT generally is the quickest method utilised. Semi-empirical methods can also be used prior to the more advanced methods in order to ensure even more accurate calculations and potentially to reduce the time for calculations that may take longer to complete.

The Cope Rearrangement

The Cope Rearrangement is one where 1,5-hexadiene undergoes a [3,3] sigmatropic shift. The reaction has been extensively researched and studied and it is now considered to proceed via a concerted mechanism with two transition states the chair or the boat. Theory shows that the chair-like transition state lies slightly lower in energy than the twist boat. Using the Hartree-Fock and DFT method one will see whether the computational calculations give corresponding and supportive data.

Optimising the Reactants and Products

A 1,5-hexadiene molecule was drawn in Gaussview, an anti-periplanar relation between the middle intersection of carbon's. This initial structure was cleaned using the CLEAN function under the edit tab in Gaussview. The molecule was then optimised under the follwing constraints:

Method: "Hartree-Fock"
Basis Set: "3-21G"
Calculation (Job Type): "Optimisation"

The returned structure was analysed and the relative energy was noted by opening the checkpoint file (*.fchk) and under the Results tab the summary sheet of the optimisation was opened. The structure was then checked to see if they had symmetry using the symmetrize function under the Edit tab, and the returned point group (if any) was noted. The operations were repeated changing the arrangement and geometry, initially, of the central 4 carbon chain. The table below depicts the structures that were optimised.

Conformer

Energy (a.u.)

Point Group

conformer 1

anti1

-231.69260

C₂

conformer 2

anti2

-231.69253

C_i

conformer 3

gauche1

-231.68771

C₁

conformer 4

gauche3

-231.69266

C₁

The initial conformer shown had the anti central carbon arrangement and was shown to have symmetry that corresponds to the C₂ point group, using the reference table ^[1] one can ascertain that this particular conformer is the anti1. The second conformer that was found corresponds to the fourth structure in the table using the method explained above and shows instead a gauche linkage between the central carbon atoms, this was determined to be the gauche3 structure. Conformer 2 and conformer 3 were determined as anti2 and gauche1 respectively. Using the two structures found initially one would assume that a low energy conformer would be one that contains anti periplanar interactions between the singly bonded carbons in the middle of the molecule as this is the one with the atoms as far apart as posible. A molecule was drawn in Gaussview interface that had an anti periplanar interaction with the terminal carbons in a different manner to those initially. However as one can see the energy that has returned was not as low as one would assume. The anti conformers generally had lower energies calculated than the gauche conformers an exception was the gauche3 conformer which when correlated with the table had the lowest energy of all the conformers. This result was slightly unexpected as one would expect the favourable arrangement would be one were the carbons are as far apart as possible to minimise electronic repulsion. The stabilisation of the gauche3 arrangement is due to the C-H σ* orbital and the overlap with the C=C π orbital. This constructive orbital orbital overlap gives extra stabilisation and therefore the lowest energy as it is only possible in this particular configuration.

The lowest anti energy conformer was then further investigated using the method above and a new more advanced method with the following constraints:

Method: DFT-B3LYP
Basis Set: 6-31G
Calculation (Job Type): Optimisation

The results from the two optimisations were collated into the table below to indicate the similarities and differences, if any, between the optimised structures.

A Comparison of Geometries for Anti 2 Conformer at different levels of Optimisations
	HF/3-21G	B3LYP/6-31G*
Energy (a.u.)	-231.69253	-234.61171
C1-C2-C3 angle	124.81	125.34
C2-C3-C4 angle	111.87	112.68
C-C bond length	1.55	1.55
C=C bond length	1.32	1.33
C2-C3/C4-C5 bond length	1.51	1.51

It appears that having modified the structure using the higher level of theory, some of the bond lengths have increased slightly in size. The angle between the middle carbons also increased indicating that the structure that was optimised using the higher level of theory has done so to minimise the energy by spatially increasing the area that the molecule covers. One should note however that it is quite difficult to compare between the different levels of theory as they took into consideration different basis sets.

Vibrational Modes

This is another manner of ensuring that the structure obtained is fully optimised as the frequencies are characterised and by ensuring that they are all real, one can be sure that the structure has a minimum energy. A frequency calculation was carried out on the twice optimised molecule to obtain the vibrational modes of the structure. The calculation was carried out as follows:

Method: DFT-B3LYP
Basis Set: 6-31G*
Calculation (Job Type): Frequency

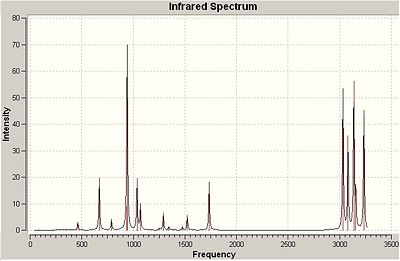
All additional keywords were removed so that the correct calculation was carried out. There were no imaginary vibrations and the IR spectrum is shown. From the frequency calculation the logfile (*.logfile) was observed in order to obtain information regarding the energy. This data allows this it to be compared to the actual experimental values and data. The Thermochemistry part of the file was considered and under the vibrational temperatures a list of energies were noted.

A Summary of Energies reported by the Frequency Calculation
Type of Energy at 298K	Energy (a.u.)
Sum of electronic and zero-point Energies	-234.46921
Sum of electronic and thermal Energies	-234.46186
Sum of electronic and thermal Enthalpies	-234.46091
Sum of electronic and thermal Free Energies	-234.50078

The energy values could be recalculated at 0K in order to compare the two different sets of energies and to see the overall affet the temperature has on the energies. This can be done in Gaussview using the Freq=ReadIsoptopes option. The energies provide both potential and kinetic energy components this allows a variety of calculations to be carried out if one wanted to investigated various aspects of the structure.

Optimising the 'Chair' and 'Boat' Transition Structures

Transition structure optimizations were set up by computing the force constants and this was combined with the use of the coordinate editor and QST2 in order to further investigate the Cope Rearrangement.

The Chair Transition State

TS(Berny) Method

A CH₂CHCH₂ allyl fragment was drawn and optimised using a simpler Hartree Fock method with a 3-21G basis set. The fragment was duplicated in Gaussview and then arranged roughly 2.20Å apart in order to try and create a chair transition state structure. An optimisation of the structure was then carried out with the same method and basis set as stated prior but with the optimisation set to TS(Berny) and the force constants were set to 'once'. There were additional keywords also put into the Gaussian calculation: Opt=NoEigen this was to ensure that if multiple negative frequencies were calculated the calculation would not abruptly stop. Time was taken to input the initial structure and arrange it in a particular way so that this particular method could provide an accurate potential energy energy surface graph/curve. If the initial structure used for this method is not in allegiance with the actual transition state inaccurate transition states can be found. The energy of the transition state was -231.61932237 a.u. and the terminal C-C bond length was 2.02Å. There was an imaginary, negative frequency observed showing that a transition state had been found and this was at -817.9 cm^-1 this again supports the idea of the structure being the transition state for the Cope rearrangement.

Frozen Coordinate Method

This time two sets of the coordinates for the terminal carbons, in the same initial di-allyl structure as above, were frozen. These terminal carbons represent the two points of the breaking and formation of the bonds in the rearrangement reaction. The Redundant Coord Editor was used in the Gaussview edit tab and the parameters for the freezing of the coordinates were Bond and Freeze coordinate. This structure was then optimised using the Hartree Fock method and the 3-21G basis set. This level is identical as the one used for the Berny method to allow for a good comparison to be made across the two methods as opposed to comparing the level of intricacy of the calculation. Because the optimisation parameters had been modified one could now view in the input line: Opt=ModRedundant This calculation was then improved by further optimising the structure obtained. The fixed bond lengths at 2.2Å were then themselves optimised by altering the calculation. Bond was selected instead of Unidentified and Derivative was selected instead of Add . An optimisation was carried out using the same level of calculation as that used in the TS(Berny) method before. The energy for the twice optimised transition state was -231.61932213 a.u. The terminal bond length for this method was still 2.02Å however if the values were left at the level produced by the calculation of 5 d.p then the Frozen Coordinate Method had slightly larger bond forming and breaking lengths. The imaginary frequency, again proving the presence of the transition state was at: -818.1cm^-1 this value is similar to that obtained using the previous method showing that the transition states for the reaction were correctly obtained. The similarity of results between both methods shows that the initial method may suffice on its own if one was investigating a series of small easily located transition states.

The Boat Transition State

The QST2 method was used in order to optimised the boat transition state. In this method one can specify the reactants and the products and the calculation can then interpolate between these two, in doing so the calculation makes an educated estimate between the two structures using a certain level of theory. The reaction was written out and the carbons in the molecules were numbered to make sure that the correct transition state was identified by the calculation as the reaction involves the rearrangement of the initial structure.

This method although more intricate does not require the initial reasonable 'guess' structure that was required for the chair transition state methods. The molecule with the C_i symmetry which was the 1,5-hexadiene with the anti-periplanar linkage (anti2) was then used as the initial structure. Then in Gaussview the molecule was copied twice in Gaussview in a way that allowed the viewing of multiple geometries. The structures were orientated so that they were viewed as below in a mirror image fashion. The carbon atoms in the structures were then numbered using the "Atom List" function in Gaussview:

The QST2 calculation was then carried out using the following constraints and level of theory:

Method: Hartree- Fock
Basis Set: 3-21G
Calculation (Job Type): Opt + Freq (Optimisation and Frequency calculation)

The calculation was then asked to 'Optimise' to a TS (QST2) which is a specific transition state that one is trying to obtain. It was observed that the job submitted failed and the molecule produced was not expected. The failure of the calculation is due to the translation of the allyl group, the calculation does not attempt a rotation of the group and this results in a more dissociated structure than initially expected. In order to aid the location of the transition state the geometries of both the product and the reactant were modified. The central dihedral angle between the middle four carbon atom was set to 0^o. The inside angle between the three carbon atom was then reduced to 100^o . The altered molecules looked like the ones below:

The calculation was repeated with the new molecules and on completion of the calculation when the checkpoint file was opened it was noted to be empty. The only lines in the file read:

No title  Bad Data: No atoms
line number:1

The anti2 molecule was loaded again and the whole process was repeated however at the initial optimisation the titles of the checkpoint files were altered ad saved along he way individually. The calculation may have been initially attempting to run the calculation on the initial single anti2 structure's checkpoint file. The final calculation that was carried out eventually located the desired boat transition state. The checkpoint file was analysed in order to confirm that the transition state had been found. A single imaginary frequency, with a negative force constant was observed the value reported was -839.73 cm^-1 . The terminal bond lengths for the optimised structure was 2.15Å and the overall energy for the molecule was -231.60280251 a.u.If one wanted to further the accuracy of the acquired transition state one could use the QST3 method with the same procedure one assumes that the interpolation between the product and reactants is done in a manner that allows a more accurate transition state to be found. The geometry of the molecule would have to be altered initially as well and the molecules would have to be numbered correctly too.

Intrinisic Reaction Coordinate

It is extremely difficult to observe the transition structures formed and predict the relative 1,5 hexadiene structures that they correspond to and hence their specific reaction paths. The IRC method, however, uses a function in Gaussian which enables the lowest energy path to be traced from the transition state to the corresponding minimum location on the potential energy surface. When considering the potential energy surface one must not forget that it is multidimensional meaning that this process is extremely useful in obtaining that said pathway. The method works by taking a series of points and then taking small steps where the gradient of the energy surface function is steepest. A checkpoint file for one of the optimised chair transition structures was opened, duplicated and saved. Under the Job Type option in Gaussian IRC was selected and a single direction was chosen due to the symmetrical nature of the reaction coordinate. The force constants were also computed at the start of the reaction the number of points was also set to 50, which is fairly good value. The IRC was stopped and having observed the procedure one could see that the reaction has not yet reached a minimum yet. However the final point had a very low RMS gradient value, there are several methods to attempt to reach the correct minima. Due to the low RMS gradient value for the final point the IRC calculation was repeated but instead of 50 points, 120 points were used. The force constants were not computed at every iteration and the length of the calculation was reasonable and the minimum was successfully obtained. The graphs and the data are presented below:

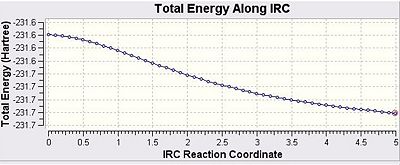
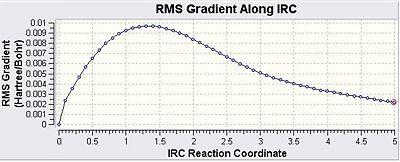
These initial graphs gave an energy of -231.68906702 a.u. and show that the minimum had not actually been correctly located the following graphs shown below have an increased number of steps:

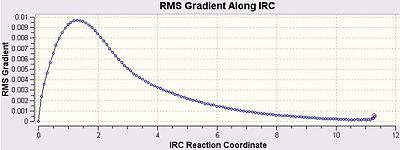
These curves appear to reach a minimum and gave an energy of -231.69175622 a.u. which is noticeably lower than the inittial energy. One can also see the differences between the final graphs in comparison to the initial graphs calculated at a fewer number of steps. The second number of steps was chosen as its just above double the initial number of iterations and hopeful the minimum should be obtained. Often however one must be wary of increasing the number of steps too much as this can lead to the calculation locating the minimum and then moving away from the located minimum due to the large and unnecessary number of steps. In some cases to prevent this the force constants would have to be computed at each step to prevent this from occurring as the force constants allow for a mathematical confirmation of a minimum.

Activation Energies

The chair and the boat transition states were re-optimised using the constraints and theory shown below in order to calculate the activation energies. However they were first optimised using the HF/3-21G level. Once these calculations were complete the calculations were repeated using the more sophisticated:

Method: DFT-B3LYP
Basis Set: 6-31G
Calculation (Job Type): Opt + Freq

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.61932	-231.46671	-231.46135	-234.55698	-234.41492	-234.40901
Boat TS	-231.60281	-231.45094	-231.44530	-234.54309	-234.40234	-234.39601
anti2	-231.69254	-231.53954	-231.53257	-234.61171	-234.46923	-234.46187

N.B The 0K values were taken from the table that was provided with reference data. ^[2]

Having looked at the summary of the data overall one can see that both levels of calculation provided similar results concerning the geometries of the optimised molecules. However the difference between he calculations is when one considers the varying energies. This difference shows the importance of not relying on one level of optimisation but ensuring the structures are optimised fully by using lower level calculations and theory and then advancing to quick but more complex levels such as the DFT "DFT-B3LYP" methods.

The activation energies for the transition states were also calculated and this was completed by noting the sum of the Thermal and the Electronic energies. For the chair the value calculated was 33.18 kcal mol^-1 and for the boat the value calculated was 41.33 kcal mol^-1

The Diels Alder Cycloaddition

Using a range of techniques discussed above the transition structures of various cycloadditions will be characterised and their molecular orbitals will be obtained and analysed. Diels Alder reactions are pericyclic reactions that can proceed in a manner of ways; from stereospecific routes which are generally allowed and non stereospecific routes which are generally forbidden. These routes are dependent on the "pi" electrons, the nodal planes allow one to predict the type of interactions that will occur between the HOMO/LUMO of the dienophile and the HOMO/LUMO of the diene.

Cis-Butadiene and Ethylene

The Cycloaddition between the diene and dienophile

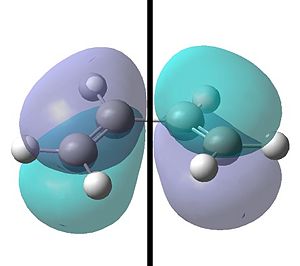
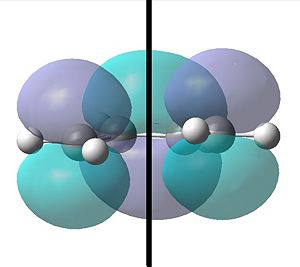
Using the semi empirical AM1 method initially and then a B3LYP/6-31G level an optimisation and a frequency was simultaneously run. The HOMO and LUMO for the cis-butadiene is shown below:

HOMO	LUMO

With respect to the plane shown the HOMO is anti-symmetric.	With respect to the plane shown the LUMO is however symmetric.

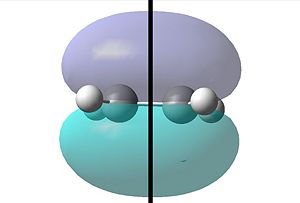
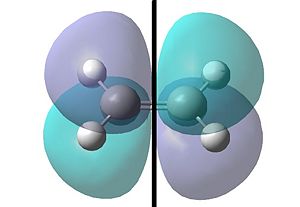
This same procedure was repeated for the ethylene reactant:

HOMO	LUMO

One can see with respect to the plane that the HOMO orbital is symmetric.	One can see that conversely with respect to the plane the LUMO orbital is anti-symmetric.

The energy for the optimised cis-butadiene structure was 0.00489 a.u. and the energy for the optimised ethylene structure was 0.02620 a.u.

The Transition State

Cyclohexa-1,3-diene 1 undergoes facile reaction with maleic anhydride 2 to give primarily the endo adduct. The reaction is supposed to be kinetically controlled so that the exo transition state should be higher in energy.

Suggested Discussion

Use this template as a guide. Screen images can be saved from the GaussView File menu.

For cis butadiene: Plot the HOMO and LUMO and determine the symmetry (symmetric or anti-symmetric) with respect to the plane.

For the ethylene+cis butadiene transition structure: Sketch HOMO and LUMO, labeling each as symmetric or anti symmetric.

Show the geometry of the transition structure, including the bond-lengths of the partly formed σ C-C bonds.

What are typical sp3 and sp2 C-C bondlengths? What is the van der Waals radius of the C atom? What can you conclude about the C-C bondlength of the partly formed σ C-C bonds in the TS.

Illustrate the vibration that corresponds to the reaction path at the transition state. Is the formation of the two bonds synchronous or asynchronous? How does this compare with the lowest positive frequency?

Is the HOMO at the transition structure s or a?

Which MOs of butadiene and ethylene have been used to form this MO? Explain why the reaction is allowed.

For the cyclohexa-1,3-diene reaction with maleic anhydride: Give the relative energies of the exo and endo transition structures. Comment on the structural difference between the endo and exo form. Why do you think that the exo form could be more strained? Examine carefully the nodal properties of the HOMO between the -(C=O)-O-(C=O)- fragment and the remainder of the system. What can you conclude about the so called “secondary orbital overlap effect”? (There is some discussion of this in Ian Fleming's book 'Frontier Orbitals and Organic Chemical Reactions').

Further discussion: What effects have been neglected in these calculations of Diels Alder transition states?

[1] ttp://www.ch.imperial.ac.uk/wiki/index.php/Mod:phys3#Appendix_1

[2] ttps://www.ch.imperial.ac.uk/wiki/index.php/Mod:phys3#Appendix_2

[1]

[2]