Rep:Mod:HZ4315
Introduction
Chemical reactions are rarely as simple as they appear and often have various potential mechanisms leading to one or more products. Therefore, in order to determine the major product of a reaction and the path taken to reach it, one must consider the properties of the reactants and the nature of the interactions between molecular orbitals (MOs). In this lab, a variety of pericyclic reactions were explored to determine the key MO interactions involved and their associated energies. This was achieved by utilising computer based optimisation strategies and subsequently investigating MO and transition state (TS) energies. In certain cases, the reaction coordinate was also considered.
Quantum Background

The Schrodinger equation is a fundamental equation which describes the quantum mechanical behaviour of a system. The time-dependant example (see Figure 1) specifically describes the evolution of a physical system over a period of time. The wavefunction component of the equation describes the position of electrons with respect to the nuclei and predicts the probability of a certain event occurring. Consequently, it can be used to determine properties of molecules and the potential reactions that they can undergo. However, within any one system, the wavefunction varies depending on which point of the potential energy surface is being considered. Therefore, in order to make use of the wavefunction, we apply the Linear Combination of Atomic Orbitals (LCAO) theory.
LCAO theory involves the combination of atomic basis functions, which are known as basis sets, in order to depict MOs. This is achieved with reasonable accuracy and can then be used to solve the Hamiltonian operator. This provides an alternative to using a complete basis set which would be far too complicated to be utilised in calculations. The use of Gaussian functions further simplifies this complex set of calculations. Used as an alternative to Slater functions, which are notoriously difficult to integrate, singular Primitive Gaussian functions can be linearly combined to give 'Contracted Gaussian' functions (see Figure 2). Primitive functions give a poor description of a wavefunction and hence are generally contracted instead. Variation of the intrinsic exponents during a Hartree-Fock calculation (see Computational Techniques for further information) then allows a potential energy minimum to be achieved which helps build an approximated 'Slater-type' orbital. This can be further improved by increasing the number of atomic basis functions per atomic orbital.[2]

Nf710 (talk) 18:55, 16 April 2018 (BST) Well done for learning the the proper definitions of the Gaussian functions used in the quantum chemical calculations.
Potential Energy Surfaces
Potential energy surfaces (PES) describe the change in energy of a system as a function of one or more other variables. For a simple system with two degrees of freedom, a minimum point corresponds to a stationary point with a first derivative of zero and a positive (greater than zero) second derivative. However, for a complex system with additional degrees of freedom, the harmonic oscillator model cannot be applied and therefore results in a more complex set of minima. Whilst there is only one true minimum (global minimum), several local minima exist with similar energies, making the global minimum difficult to find. To put it into context, a system with N atoms has 3N-6 degrees of freedom and hence, the complexity increases very quickly. As mentioned above, the fact that this system cannot be modelled as a harmonic oscillator means that the associated force constant is difficult to calculate using the second derivative. Instead, a Hessian matrix is used. The matrix consists of second-order partial derivatives of the energy of the molecule in question and diagonalisation of this matrix gives rise to the force constants. The constants are eigenvectors and arrise from the linear combination of the degrees of freedom. Since all force constants are positive at a minimum, the corresponding frequencies must also be positive. Therefore, conducting frequency calculations and ensuring all the values are positive allows us to correctly determine the minimum.
In contrast, the transition state (TS) corresponds to a maximum on the minimum energy pathway. For a simple system with two degrees of freedom, derivatives are again used to determine the TS. Similarly to the minimum, the TS will have a first derivative of zero. However, unlike the minimum, the second derivative will be positive for all degrees of freedom except one. The particular one will therefore have a negative force constant and frequency. Whilst the systems explored in this lab were more complex (and therefore the second derivative alone is not conclusive), a similar trend is witnessed during the use of a Hessian Matrix and therefore, the position of the TS was confirmed when a negative frequency was seen.
Nf710 (talk) 19:31, 16 April 2018 (BST) Great understanding of the PES. Importantly when you diagonalise the Hessian Matrix the eigenvectors you get are the normal modes which are linear combinations of the degreees of freedom. This is why they look like vintrations when you move back and forth on then vector.
Computational Techniques
Hartree-Fock Method
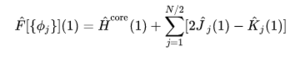
The Hartree-Fock method is generally used to solve the time-independant Schrodinger equation for a many-electron system. This is achieved using LCAO to obtain a one-electron wavefunction which describes optimised MOs. Since the electron-electron repulsion term in the molecular Hamiltonian requires the coordinates of two separate electrons, all terms the Hamiltonian except the nuclear-nuclear repulsion term are re-expressed as a sum of one-electron operators in the Hartree-Fock operator (see Figure 3). Amongst other simplifications, it utilises the Born-Oppenheimer approximation and the mean-field approximation. The later implies that the electrons within the system experience an averaged field stemming from all the electrons within the system. Whilst this simplifies the calculation, it also means that that instantaneous interactions between electrons are disallowed and the repulsive field experienced by a particular electron is greater than it should be since the electron itself has not been neglected. Various methods which combine to form the 'post-Hartree-Fock' have been explored to improve this.
The semi-empirical PM6 optimisation method used during this lab is based on the Hartree-Fock method. The use of approximations and empirical data improves the efficiency of calculations and therefore allows more complex molecules to be investigated.
B3LYP Optimisation
B3LYP optimisation is a hybrid optimisation technique involving density functional theory (DFT) and the previously mentioned Hartree-Fock method. The former allows the properties of many-electron systems to be determined by using 'functionals'. Functionals are in essence, functions of functions (specifically the function of spatially dependant electron density). Used in conjunction with the Hartree-Fock method, a relatively inexpensive and efficient method of optimisation which incorporates both the exchange and electron correlation functionals is achieved.
Nf710 (talk) 19:35, 16 April 2018 (BST) You have clearly read beyond the script here well done. You could have gone into more detail by talking about when the J and K are. Excellent section.
Exercise 1: Reaction of Butadiene with Ethylene

In this exercise, the Diels-Alder pericyclic reaction between cis-butadiene and ethylene (see Scheme 1) was investigated. This involved the following:
1. Optimisation of cis-butadiene and ethylene to their minimum energy ground states.
2. Optimisation of the transition state (TS) to its minimum energy ground state followed by a TS (Berny) optimisation.
3. IRC analysis of the reaction.
4. Optimisation of the cyclohexene product.
All optimisations were conducted using a semi-empirical PM6 basis set and in accordance with Method 1 and 2. During the ground state optimisations, the distance between the terminal carbons on cis-butadiene and ethylene was set at 2.2Å (via the Redundant Coordinates tab).
Key Molecular Orbitals
Reactants
| Ethylene | Butadiene | |||||
|---|---|---|---|---|---|---|
| HOMO | ||||||
| LUMO |
Transition State
| HOMO (-1) | HOMO | LUMO | LUMO (+1) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Transition State |
Molecular Orbital Diagram
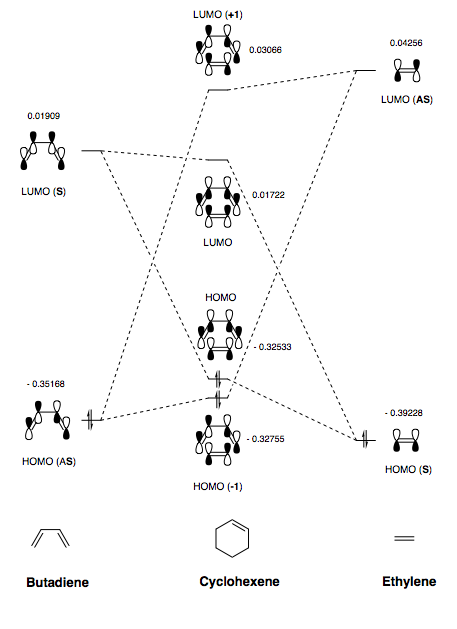
(Fv611 (talk) You are missing the symmetry labels on this MO diagram.)
Once the TS was optimised, the relevant molecular orbitals and energies could be seen in Gaussview. These were used to produce the MO diagram for the reaction between cis-butadiene and ethylene (see Figure 4). It is useful in determining the bonding and non-bonding orbital interactions. Typically, for a reaction to 'allowed', the frontier molecular orbitals that are interacting must be similar in energy and share the same symmetry. This ensures that the overlap integral is zero since there is no net constructive or deconstructive interference experienced. Therefore, the allowed interactions are as follows:
| Allowed | Forbidden | Orbital Overlap Integral | |
|---|---|---|---|
| Symmetric-Symmetric | X | Non-zero | |
| Asymmetric-Asymmetric | X | Non-zero | |
| Symmetric-Asymmetric | X | Zero |
(Fv611 (talk) Be carful: your state in your discussion that the orbital overlap is zero for same symmetry orbitals, while you say the opposite in the table above.)
With this in mind, the relevant orbital interactions can be found in Table 3 below:
| Ethylene/Butadiene Pair | Bonding Interaction | Anti-bonding Interaction |
|---|---|---|
| HOMO (AS)/LUMO (AS) | HOMO (-1) | LUMO (+1) |
| LUMO (S)/HOMO (S) | HOMO | LUMO |
The first point of interest regarding the MO diagram in Figure 4 is the relative displacement of the TS MOs in relation to the reactant MOs. Since TSs occur at a maximum on the PES, the energy of the MOs is expected to be higher than those of the reactants which is indeed the case. This difference in energy is defined as the activation energy. Furthermore, as indicated above, a Butadiene/Ethylene (HOMO/LUMO) interaction yields the TS Bonding (HOMO (-1)) and Anti-bonding (LUMO (+1)) interactions whilst a Butadiene/Ethylene (LUMO/HOMO) interaction yields the TS Bonding (HOMO) and Anti-bonding (LUMO) interactions. The splitting observed for the former is greater than the latter which stems from the frontier orbitals being more similar in energy and therefore interacting more strongly. The resulting HOMO (-1) and LUMO (+1) energies indicate that the reaction proceeds via a normal electron demand Diels-Alder mechanism. The fact that the HOMO (-1) interaction has a higher energy w/r to the butadiene HOMO and the LUMO (+1) has a lower energy w/r to the ethylene LUMO shows that the diene is electron rich compared to the dienophile.
Bond Lengths
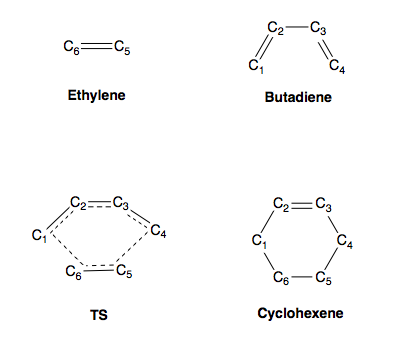
The relevant bond lengths (in Å) for the molecules shown in Figure 5 can be found in Table 4 below:
| Ethylene | Butadiene | TS | Cyclohexene | |
|---|---|---|---|---|
| C1-C2 | - | 1.33358 | 1.37983 | 1.50033 |
| C2-C3 | - | 1.47083 | 1.41116 | 1.33758 |
| C3-C4 | - | 1.33357 | 1.37971 | 1.50033 |
| C4-C5 | - | - | 2.11553 | 1.54002 |
| C5-C6 | 1.32731 | - | 1.38178 | 1.54063 |
| C6-C1 | - | - | 2.11393 | 1.54002 |
Before discussing the changes in bond lengths witnessed in the reaction, it is worth noting some typical bond lengths and radii for varying carbon hybridisations:
- Bond length (sp3-sp3) = 1.54Å
- Bond length (sp3-sp2) = 1.50Å
- Bond length (sp2-sp2) = 1.34Å
- Carbon VdW radius = 1.7Å
Analysis of the relative bond lengths raise some key points. Firstly, the ethylene double bond (corresponding to C5-C6 in ethylene and the TS) is seen to become longer during the progression towards the product. This is expected as the bond undergoes conversion from a π bond to a sigma bond whereby it ultimately converges at the expected value of 1.54Å. Likewise, the butadiene double bonds (C1-C2 and C3-C4) also elongate for the same reason. They do however converge at a slightly shorter length (1.50Å) which is due to the double bond forming between them (C2-C3). This results in a sp3-sp2 type bond. The shortening of the C2-C3 bond confirms the conversion from a sigma bond to a π bond with the bond ultimately converging close to the expected value of 1.34Å.
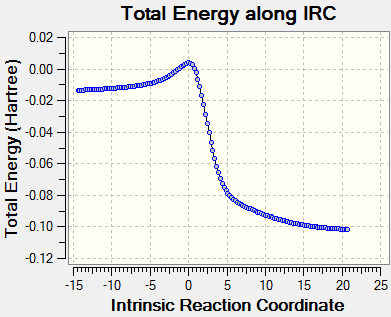
The changes witnessed in the bond lengths do coincide with transition state theory as the TS structure lies between the structures of the reactants and product. This can be confirmed by considering the lengths of C4-C5 and C6-C1. The observed length of 2.1Å is shorter than the typical distance maintained between atoms (i.e. 2 x vdW radius = 1.7 x 2 = 3.4Å) which indicates an interaction between orbitals. However, analysis of the IRC (see Figure 6) shows the TS to be closer in energy to the reactants than products.

With the TS being closer in energy to the reactants, an early TS is witnessed with the structure resembling that of the reactants. This can be confirmed by considering the bond length values in the TS. C1-C2 and C3-C4 have lengths of ~1.38Å which is closer to the value of ~1.33Å in butadiene than ~1.50Å in cyclohexene. Overall, the reaction proceeds like so:
Transition State Vibrations
In order to identify the correct TS, TS (berny) optimisations were conducted until a structure exhibiting a single negative vibrational frequency was witnessed. The animation shown in Figure 8 corresponds to a negative frequency of -948.37 cm-1. Since the terminal carbons on both molecules approach each other in a concerted fashion, the reaction must be synchronous.
Exercise 2: Reaction of Cyclohexadiene with 1,3-Dioxole
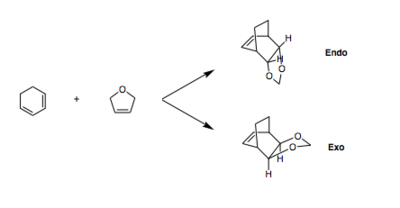
In this exercise, the pericyclic reaction between 1,3-dioxole and cyclohexadiene was investigated. Both the endo and exo products of the reaction were considered. The investigation involved:
1. Optimisation of the reactants to their minimum energy ground states (PM6 and B3LYP).
2. Optimisation of the TS to its minimum energy ground state followed by a TS (Berny) optimisation (PM6 and B3LYP).
3. IRC analysis of the reaction (PM6 only).
4. A single point energy (SPE) calculation on the IRC product.
5. Optimisation of the product (PM6 and B3LYP).
Method 2 was primarily used throughout. During ground state optimisations, the distance between the terminal carbons was again set at 2.2Å.
Key Molecular Orbitals
Reactants
| Cyclohexadiene | 1,3-Dioxole | |||||
|---|---|---|---|---|---|---|
| HOMO | ||||||
| LUMO |
Transition State
Endo
| HOMO (-1) | HOMO | LUMO | LUMO (+1) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TS (Endo) |
Exo
| HOMO (-1) | HOMO | LUMO | LUMO (+1) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TS (Exo) |
Comparison
| Energy (Endo) | Energy (Exo) | Energy Difference (Endo - Exo) | |
|---|---|---|---|
| LUMO(+1) | 0.01543 | 0.01019 | 0.00524 |
| LUMO | -0.00462 | -0.00699 | 0.00237 |
| HOMO | -0.19051 | -0.18560 | -0.00491 |
| HOMO(-1) | -0.19648 | -0.19801 | 0.00153 |
From Table 7 we can see a difference of -0.00491 Hartrees between the endo and exo HOMO energy levels. This indicates that the endo TS is more stable (since it has a lower energy HOMO level). This stems from secondary orbital interactions experienced between the oxygen lone pair within the dioxole ring and the pi bonds within the cyclohexadiene. These are not possible in the exo TS.
Molecular Orbital Diagrams
Once the relevant MOs and their associated energies were obtained in Gaussview, the MO diagrams below (Figure 9 and Figure 10) were constructed.

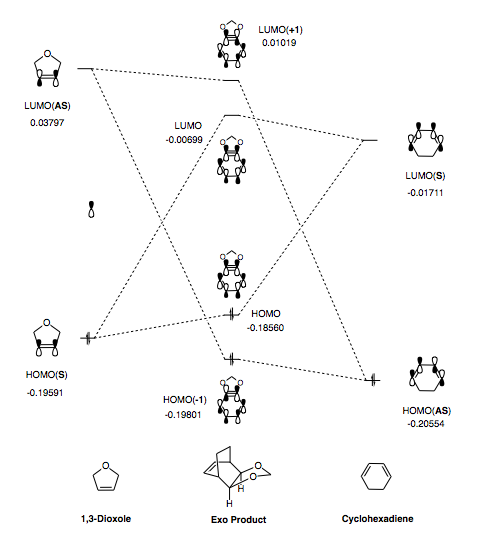
The MO diagrams above shed light on the possible mechanism of this Diels-Alder reaction (i.e. normal vs inverse electron demand). In terms of the splitting witnessed, the interaction between the HOMO of cyclohexadiene (diene) and the LUMO of 1,3-dioxole (dienophile) appears to be the strongest. This is characteristic of 'inverse electron demand'. However, in order to confirm this, quantitative analysis is required. Since the MOs seen in Table 5 and Table 6 arise from different potential energy surfaces, their associated Hamiltonian potentials and relative energies will also vary. Therefore, in order to carry out the necessary analysis, a single point energy (SPE) calculation is required.
Single Point Energy (SPE) Calculation
Endo
| HOMO (-1) | HOMO | LUMO | LUMO (+1) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TS (Endo) |
Exo
| HOMO (-1) | HOMO | LUMO | LUMO (+1) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TS (Exo) |
Discussion
| Energy (Endo) | Energy (Exo) | |
|---|---|---|
| LUMO(+1) | 0.03219 | 0.02979 |
| LUMO | 0.02288 | 0.02110 |
| HOMO | -0.31696 | -0.32207 |
| HOMO(-1) | -0.32135 | -0.32215 |
The SPE calculation was performed on the last frame of the associated IRC for each transition state. The resulting MOs share a common potential energy surface and can therefore be compared quantitatively. Analysis of the MO energies confirms the 'inverse electron demand' nature of this reaction with the 1,3-dioxole (dienophile) having a higher energy HOMO in both TSs. This stems from the electron rich nature of 1,3-dioxole which acts as an electron donating group. Typically, electron donating dienophiles experience an increase in energy for both their HOMO and LUMO MOs. This is indeed the case here with the dienophile's oxygen atom donating electrons into the diene's π* and consequently raising its own HOMO and LUMO (π and π* respectively).
Energy Analysis/Reaction Coordinate
In order to determine the reaction coordinate, the following energies were determined:
1. Reactants - This was achieved by individually optimising cyclohexadiene and 1,3-dioxole (B3LYP level) then adding the energies together.
2. Transition states - Obtained using a TS (Berny) calculation (B3LYP level).
3. Products - Obtained by optimising the product frame from the IRC (B3LYP level)
The results of these calculations are shown in Table 11 below:
| Endo Energy (KJ/mol) | Exo Energy (KJ/mol) | |
|---|---|---|
| Reactants | -1313781.98 | -1313781.98 |
| Transition State | -1313622.16 | -1313614.31 |
| Product | -1313849.37 | -1313845.78 |
| Ea | 159.82 | 165.46 |
| ΔHr⊖ | -67.39 | -63.80 |
These energies give rise to the following reaction coordinate:
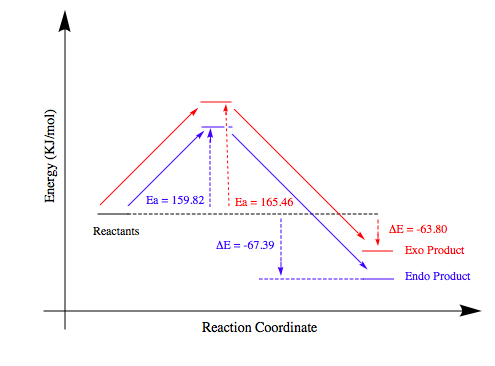
From this reaction coordinate we can infer that the endo reaction/product will dominate over its exo counterpart. The activation energy (Ea) for the exo reaction is 5.64 KJ/mol higher than the endo reaction and the exo product is also 3.59 KJ/mol higher in energy. Consequently, the endo reaction is both thermodynamically and kinetically favoured. In terms of the thermodynamics, the exo product experiences steric clash between the protons contained within the dioxole and the carbon based bridge. This is avoided by the endo conformer. Kinetically, the endo reaction has a lower Ea which stems from the secondary orbital interactions discussed previously.
Product Energy Log Files:
Endo: File:HZ4315 EX2 ENDOPROD(6-31G).LOG
Exo: File:HZ4315 EX2 EXOPROD(6-31G).LOG
Nf710 (talk) 19:41, 16 April 2018 (BST) Excellent section. Your single point energy analysis was done extremely well. and you have got the correct energies and therefore the correct conclusions. Well done.
Exercise 3: Diels-Alder vs Cheletropic
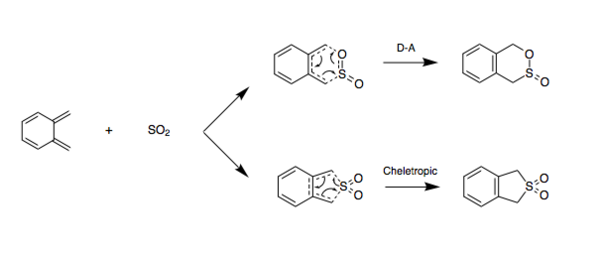
In this exercise, the endocyclic and exocyclic Diels-Alder reactions between o-xylylene and sulfur dioxide were investigated alongside the cheletropic alternative reaction. in contrast to the previous exercises, Method 3 was used. The investigation of each pathway involved:
1. Optimisation of the products to their minimum ground state energy.
2. Breaking of the C-S and C-O bonds to obtain a guess TS.
3. Optimisation of the TS to its minimum ground state energy followed by a TS (Berny) optimisation.
4. IRC analysis.
5. Establishment of the reaction coordinates using reaction energies.
All optimisations were carried at the PM6 level. For ground state optimisations, the C-S and C-O bond lengths were frozen at 2.4Å and 2.0Å respectively.
IRC Analysis
Diels-Alder: Endo
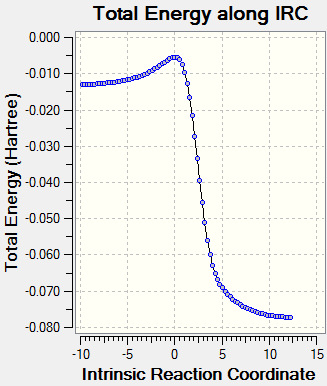

Diels-Alder: Exo
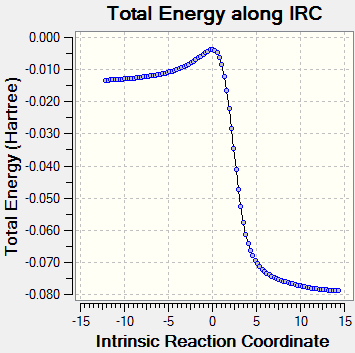
Cheletropic
(These diagrams can be grouped in a table for clarity Tam10 (talk) 14:12, 4 April 2018 (BST))
Energy Analysis/Reaction Coordinate
Similarly to Exercise 2, in order to determine the reaction coordinate, a series of optimisations (PM6 level) were conducted and the resulting energies can be found in Table 12 below:
| Endo Energy (KJ/mol) | Exo Energy (KJ/mol) | Cheletropic Energy (KJ/mol) | |
|---|---|---|---|
| Reactants | 158.25 | 158.25 | 158.25 |
| Transition State | 237.76 | 241.75 | 260.08 |
| Product | 56.98 | 56.32 | 0.0026 |
| Ea | 79.51 | 83.5 | 101.83 |
| ΔHr⊖ | -101.27 | -101.98 | -158.25 |
There energies gave rise to the following coordinate:
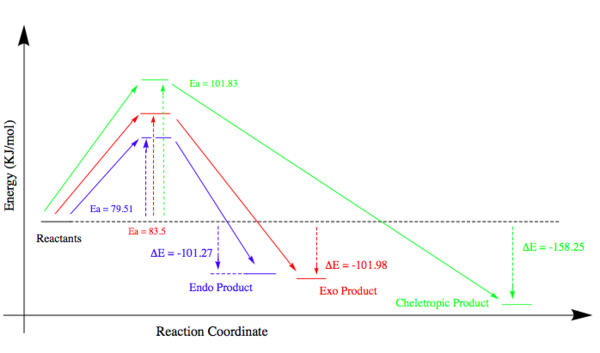
Consideration of the energies and reaction coordinates of the three pathways gives rise to some important points. In terms of the activation energies and the relative TS energies, the endo pathways has the smallest (Ea = 79.51 KJ/mol), making it kinetically favourable. As mentioned in Exercise 2, secondary orbital interactions involving the donation of electrons from heteroatoms within a dienophile to the diene can help stabilise a TS. Therefore, it is possible that the oxygen atom within the SO2 molecule is donating its lone pair into the π* orbital of o-xylylene. However, in this case, the most stable product is actually reached via the cheletropic pathway. A product energy of 0.0026 KJ/mol is 56.955 KJ/mol and 56.317 KJ/mol lower than the endo and exo products respectively. Since aromaticity is restored in all three products, the reason for the stability of the cheletropic product lies with the nature of the bonds and rings. Firstly, by forming a five membered ring with only the sulfur atom contained within it, an additional strong S=O bond is preserved. The formation of an addition C-O bond does not compensate for breaking this bond in the Diels-Alder reactions. Furthermore, the five membered ring also relieves the strain experienced in the six membered ring which stems from the larger size of sulfur atoms compared to carbon atoms.
Alternative Reaction
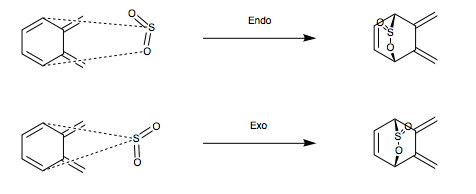
As shown in Scheme 4, an alternative, endocyclic reaction between o-Xylylene and Sulfur Dioxide is possible. Therefore, to check its thermodynamic viability, optimisations were conducted on the products, TS and reactants (PM6 level) using Method 3 and IRC and energy analysis was subsequently carried out.
IRC Analysis
Endo
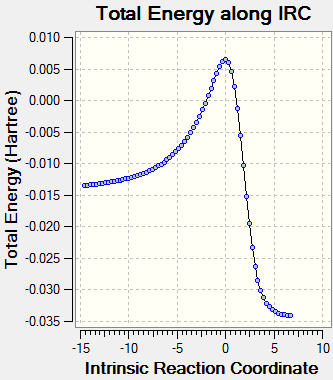
Exo

Energy Analysis
| Endo Energy (KJ/mol) | Exo Energy (KJ/mol) | |
|---|---|---|
| Reactants | 158.25 | 158.25 |
| Transition State | 267.98 | 275.82 |
| Product | 172.25 | 177.49 |
| Ea | 109.73 | 117.57 |
| ΔHr⊖ | 14.00 | 19.24 |
The first point to note from these energies is the increase in energy of both the endo and exo TSs compared to those witnessed in the typical exocyclic Diels-Alder and cheletropic reactions. This may be due to the disruption to aromaticity experienced when the product forms. In the exocyclic examples. the products are re-aromatised however, this is not the case here. Consequently, we would expect the TSs to be comparitively destablised. Furthermore, the enthalpy of reaction is positive which indicates that the reaction is endothermic. Consequently, the reaction would not be thermodynamically favourable.
Log Files
Reactants:
SO2: File:HZ4315 SO2.LOG o-Xylylene: File:HZ4315-XYLYLENE.LOG
Exocyclic Reaction (Endo):
TS: File:HZ4315-MAIN-ENDO(TS).LOG Product: File:HZ4315-MAIN-EXO-PROD.LOG
Exocyclic Reaction (Exo):
TS: File:HZ4315-MAIN-EXO(TS).LOG Product: File:HZ4315-MAIN-EXO-PROD2.LOG
Exocyclic Reaction (Cheletropic):
TS: File:HZ4315-MAIN-CHEL-TS.LOG Product: File:HZ4315-MAIN-CHEL-PROD.LOG
Endocyclic Reaction (Endo):
TS: File:HZ4315-ALT-ENDO-TS.LOG Product: File:HZ4315-ALT-ENDO-PROD.LOG
Endocyclic Reaction (Exo):
TS: File:HZ4315-ALT-EXO-TS.LOG Product: File:HZ4315-ALT-EXO-PROD.LOG
Further Work: Electrocyclic Ring Closure of [1,1']bicyclohexyl-1,1'-diene
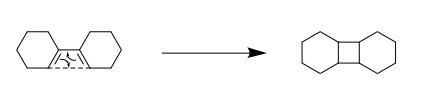
As an extension, the mode of the electrocyclic ring closure of [1,1']bicyclohexyl-1,1'-diene (Diene X) (see Scheme 5) was explored. Typically, under photochemical conditions, the closure occurs via a disrotatory mechanism whereby the new C-C bond forms as a result of suprafacial approach (see Figure 21). This stems from the photochemical excitation of an electron from the original HOMO of one of the diene's double bonds into the LUMO. This essentially makes this the new HOMO and since it is now similar in energy to the corresponding LUMO on the other double bond, orbital interactions can occur, leading to the formation of a new bond. However, in this computational lab, reactions were modelled using PM6 optimised reactants, TSs and products. Since PM6 optimisations are under thermal conditions, the mode of ring closure for systems with 4n π-electrons is expected to be conrotatory. To confirm this, optimisations of the reactants, TS and product were carried out after which IRC and energy analysis was conducted.
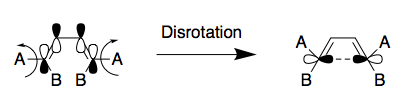
(Why are you showing disrotation when this mechanism is conrotation on ground state?)
Transition State Vibration
As was the case throughout the lab, the TS was confirmed by the presence of a single, negative frequency. In this case, it occurred at -494.99 cm-1 and can be seen in Figure 23 below.

IRC Analysis

From the IRC movie shown above it is clear that both hydrogen atoms situated at each double bond within Diene X rotate in a clockwise fashion, making the ring closure conrotatory. This is expected for systems with 4n π-electrons under thermal conditions. Since Diene X has 4 π-electrons, a value of zero for 'n' satisfies the equation and hence, the computational analysis matches the theory. The schematic representation for this can be seen in Figure 25 below.

Energy Analysis
| Reactant (kJ/mol) | Transition State (kJ/mol) | Product (kJ/mol) | Ea (kJ/mol) | ΔHr⊖ (kJ/mol) |
|---|---|---|---|---|
| 740.07 | 802.09 | 603.42 | 62.02 | -136.65 |
The negative ΔHr⊖ value witnessed indicates that the reaction is exothermic, making it thermodynamically viable.
Conclusion
Using both the PM6 (semi-empirical) and B3LYP, a variety of pericylic reactions were modelled and explored to determine the necessary properties for the reaction to occur and the likely path it progresses through. In Exercise 1, the Diels-Alder reaction between cis-butadiene and ethylene was investigated. Considering that the overlap integral for two orbitals was required to be zero, it was found that both interacting orbitals must share the same symmetry. Subsequent analysis of the relevant MOs and their energies showed the diene's MO energy to increase in the TS whilst the dienophile's MO energies fell, indicating that the reaction proceeds via normal electron demand. Analysis of the IRC and bond lengths also suggested that the TS more closely resembled the reactants, making it an early TS.
In contrast, the Diels-Alder reaction between 1,3-dioxole and cyclohexadiene explored in Exercise 2 proceeded via an inverse electron demand mechanism. This was again inferred by comparing the energies of the MOs in the reactants and in the TS. It was found that the dienophile's frontier MOs were raised in energy, making the interaction between its HOMO and the diene's LUMO stronger. To confirm this, a single point energy calculation was performed. In terms of the thermodynamic and kinetic products, the endo product satisfied both. Thermodynamically, the endo product had the lowest energy, whilst kinetically, the endo route had the lowest activation energy.
Exercise 3 explored the reaction between o-xylylene and sulfur dioxide. The possible reaction pathways were Diels-Alder and cheletropic reactions. Within the Diels-Alder reaction, depending on the approach of SO2, both exocyclic and endocyclic reactions were possible. Comparison of the three reactions showed the endo product from the exocyclic pathway to have the lowest activation energy, making the product kinetically favourable. This may have stemmed from secondary orbital interactions between the oxygen lone pair and the alkene π*. Thermodynamically, the cheletropic product was favoured as it had the lowest energy. This was attributed to the retention of an additional strong S=O bond as well as reduced strain within the five-membered heterocyclic ring compared to its six-membered counterpart.
As an extension, the electrocyclic ring closure of Diene X (see Further Work for its chemical name) was explored. The reaction was expected to be conrotatory under thermal conditions since the diene has 4π electrons (and thus satisfies the 4n equation where n =0). Analysis of the IRC confirmed this with the hydrogen atoms on the diene moving in a clockwise manner. Analysis of the reaction energies also showed the reaction to be exothermic.
References
1. Https://en.wikipedia.org/wiki/Schr%C3%B6dinger_equation
2. http://www.helsinki.fi/kemia/fysikaalinen/opetus/jlk/luennot/Lecture1.pdf
3. https://en.wikipedia.org/wiki/Gaussian_orbital
4. https://en.wikipedia.org/wiki/Hartree%E2%80%93Fock_method
