NH₃ Optimisation

NH₃

Information

Ammonia

More Info

Calculation Method

RB3LYP

Basis Set

6-31G(d,p)

Final Energy E(RB3LYP)

-56.55776873 a.u.

RMS Gradient Norm

0.00000486 a.u.

Point Group

C3V

N-H Bond Distance

1.02 Å

H-N-H Bond Angle

106°

         Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000072     0.001800     YES
 RMS     Displacement     0.000035     0.001200     YES

Vibration Modes

Vibration Modes of NH₃ molecule
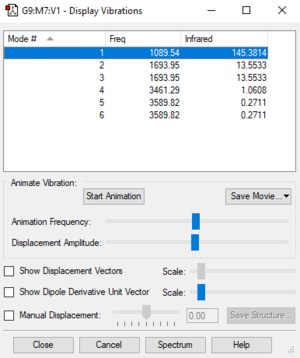
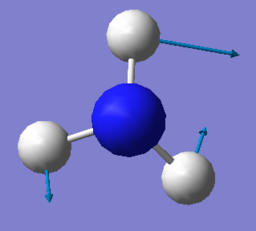
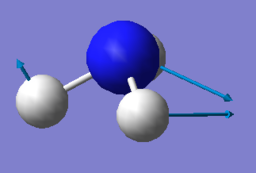
Mode	1	2	3
Wavenumber cm^-1	1090	1694	1694
Symmetry	A1	E	E
Intensity	145	14	14
Image
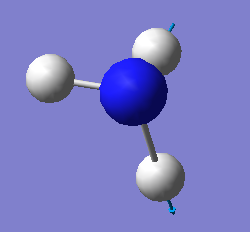
Mode	4	5	6
Wavenumber cm^-1	3461	3590	3590
A1	E	E
Intensity	1	0	0
Image

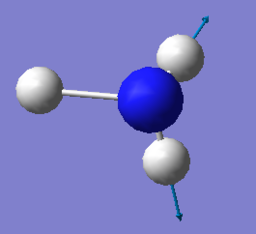
From the 3N-6 rule, 3 modes are expected to be seen.

6 modes are seen in the vibration display, with mode 2 and mode 3 are degenerate and mode 5 and mode 6 are degenerate.

Mode 1, 2 amd 3 are bending vibrations and mode 4, 5 and 6 are bending vibrations.

Mode 1 and mode 4 are highly symmetric.

Mode 1 is the "umbrella" mode.

3 bands are expected to be seen in an experimental spectrum gaseous ammonia, but since the last band has extremely low intensity, it might not be noticeable in the spectrum.

Atomic Charges

Charge on N atom: -1.125e

Charge on H atoms: 0.375e

H₂ Optimisation

H₂

Information

Hydrogen

More Info

Calculation Method

RB3LYP

Basis Set

6-31G(d,p)

Final Energy E(RB3LYP)

-1.17853935 a.u.

RMS Gradient Norm

0.00003809 a.u.

Point Group

DinfH

H-H Bond Distance

0.74 Å

H-N-H Bond Angle

180°


         Item               Value     Threshold  Converged?
 Maximum Force            0.000066     0.000450     YES
 RMS     Force            0.000066     0.000300     YES
 Maximum Displacement     0.000087     0.001800     YES
 RMS     Displacement     0.000123     0.001200     YES

N₂ Optimisation

N₂

Information

Nitrogen

More Info

Calculation Method

RB3LYP

Basis Set

6-31G(d,p)

Final Energy E(RB3LYP)

-109.52412868 a.u.

RMS Gradient Norm

0.00000365 a.u.

Point Group

DinfH

N-N Bond Distance

1.11 Å

N-N Bond Angle

180°


         Item               Value     Threshold  Converged?
 Maximum Force            0.000006     0.000450     YES
 RMS     Force            0.000006     0.000300     YES
 Maximum Displacement     0.000002     0.001800     YES
 RMS     Displacement     0.000003     0.001200     YES

Structure and Reactivity

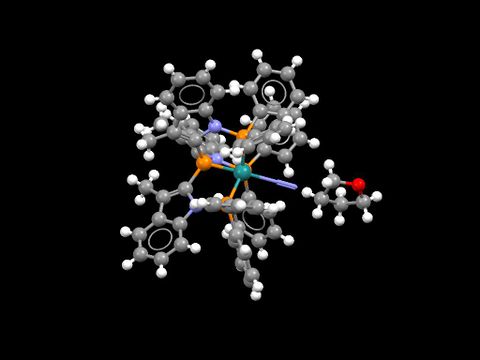
Molecular formula: C₆₃H₅₁N₅P₄Ru, C₄H₈O

Unique Identifier: [| DEKFUX]

N-N bond length: 1.086(6)Å

The N-N bond length is shorter than that recorded fot the N₂ molecule, 1.11 Å.

The crystal structure is shorter than the computational distances, since in the metal complex, the N₂ molecule is attached to a transition metal, Ruthenium, and the molecule is solvated by tetrahydrofuran. The N₂ molecule is partially negative since N has high electronegativity, therefore it repels the Oxygen atom in the solvate. In a crystalline (solid) structure, the space between molecules is compressed, hence the N-N bond length is shortened, while N₂ is in gas state, hence N₂ molecule has longer bond length.

N₂ has a literature of 1.0976 ± 0.0002 r_e, hence the computational value is not very accurate as well.

Reference:[| Tables of Interatomic Distances and Configuration in Molecules and Ions, L.E. Sutton, ed., London: The Chemical Society, 1958.], page 70.

Haber-Bosch Process

N₂ + 3H₂ -> 2NH₃

Energy Calculation

E(NH₃)= -56.5577687 au

2*E(NH₃)= 2*(-56.5577687)= -113.1155374 au

E(N₂)= -109.5241287 au

E(H₂)= -1.1785394 au

3*E(H₂)= 3*(-1.1785394)= - 3.5356182

ΔE=2*E(NH₃)-[E(N₂)+3*E(H₂)]= (-113.1155374)-[(-109.5241287)+(- 3.5356182)]= -0.0557905 au

ΔE= (-0.0557905)au * 2625.5 kJmol^-1/au= -146.4779578 kJmol^-1= -146.5 kJmol^-1

Since ΔE is negative, the process is exothermic, hence the product is in lower energy state than the reactants. As a result, the ammonia product is more stable.

Chosen Molecule: SH₂

SH₂

Information

Hydrogen sulfide

More Info

Calculation Method

RB3LYP

Basis Set

6-31G(d,p)

Final Energy E(RB3LYP)

-399.39162414 a.u.

RMS Gradient Norm

0.00012068 a.u.

Point Group

C2V

S-H Bond Distance

1.34737 Å

H-S-H Bond Angle

92.681


         Item               Value     Threshold  Converged?
 Maximum Force            0.000175     0.000450     YES
 RMS     Force            0.000145     0.000300     YES
 Maximum Displacement     0.000472     0.001800     YES
 RMS     Displacement     0.000386     0.001200     YES

Vibration Modes

Vibration Modes of SH₂ molecule
Mode	1	2	3
Wavenumber cm^-1	1224	2692	2712
Symmetry	A1	A1	B2
Intensity	5	7	9
Image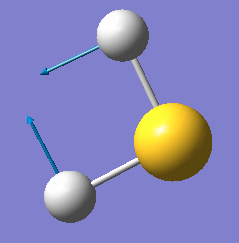

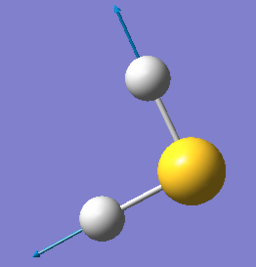
Atomic Charges

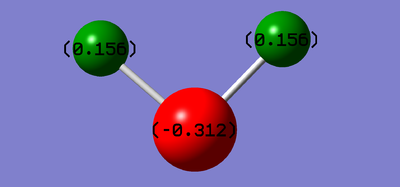
Charge on S atom: -0.312e

Charge on H atoms: 0.156e

Energy Calculation

S + H₂ -> SH₂

E(SH₂)= -399.3916241 au

E(S)= -398.0425733 au (result obtained from optimising a single S atom)

E(H₂)= -1.1785394 au

ΔE=E(SH₂)-[E(S)+E(H₂)]= (-399.3916241)-[(-398.0425733)+(-1.1785394)]= -0.1705114 au

ΔE= (0.1705114)au * 2625.5 kJmol^-1/au= -447.6776807 kJmol^-1= -477.7 kJmol^-1

Molecular Orbitals

Molecular Orbitals of SH₂ molecule
Summary of MOs	No. of MOs	Image of MOs
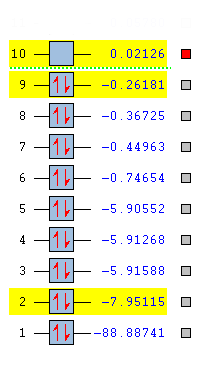
	10
	9
	8
	7
	6
	5
	4
	3
	2
	1

The highest occupied molecular orbital (HOMO) in this molecule is MO no. 9, and the lowest unoccupied molecular orbital (LUMO) in this molecule is 10

From MO=6 and onwards, the ovelap occurs between the valence AOs of the atoms, hence the overlap is more significant.

Valence AOs from S atom: 3s, 3p_x, 3p_y, 3p_z

Two 1s orbitals from the two H atoms overlap in-phase and out-of-phase respectively, creating two Ligand Group Orbitals.

3s orbital in S overlap in phase with the in-phase LGO to from MO=6, a bonding orbital.

MO=7 is contributed by the 3p_y orbital from S atom and the out-of-phase LGO orbital from the two H atoms overlapping constructively.

MO=8 is contributed by 3s and 3p_z from the S atom and the in-phase LGO overlapping constructively.

For MO=9, the orbital is simply a non-bonding 3p_x orbital from the S atom. This is the HOMO of the SH₂ molecule.

For MO=10, it is resulted from the 3p_y orbital in S overlapping with the out-of-phase LGO destructively, forming an anti-bonding orbital. This is the LUMO of the SH₂ molecule.

Marking

Note: All grades and comments are provisional and subject to change until your grades are officially returned via blackboard. Please do not contact anyone about anything to do with the marking of this lab until you have recieved your grade from blackboard.

Wiki structure and presentation 1/1

Is your wiki page clear and easy to follow, with consistent formatting?

YES

Do you effectively use tables, figures and subheadings to communicate your work?

YES - good use of tables.

NH3 0/1

Have you completed the calculation and given a link to the file?

No link to the log file.

Have you included summary and item tables in your wiki?

YES

Have you included a 3d jmol file or an image of the finished structure?

YES

Have you included the bond lengths and angles asked for?

YES

Have you included the “display vibrations” table?

YES

Have you added a table to your wiki listing the wavenumber and intensity of each vibration?

YES

Did you do the optional extra of adding images of the vibrations?

YES

Have you included answers to the questions about vibrations and charges in the lab script?

Good answers to the vibrations questions - there are two peaks visible as vibrations 4, 5, and 6 have too low an intensity to be seen. You didn't explain why the charges on the atoms are there - nitrogen is more electronegative than hydrogen.

N2 and H2 0/0.5

Have you completed the calculations and included all relevant information? (summary, item table, structural information, jmol image, vibrations and charges)

YES

However you have given a bond angle of 180 for N2 and H2, there are no bond angles in diatomic molecules. Bond angles involve exactly 3 atoms.

Crystal structure comparison 0.5/0.5

Have you included a link to a structure from the CCDC that includes a coordinated N2 or H2 molecule?

YES

Have you compared your optimised bond distance to the crystal structure bond distance?

YES

Haber-Bosch reaction energy calculation 1/1

Have you correctly calculated the energies asked for? ΔE=2*E(NH3)-[E(N2)+3*E(H2)]

YES

Have you reported your answers to the correct number of decimal places?

YES

Do your energies have the correct +/- sign?

YES

Have you answered the question, Identify which is more stable the gaseous reactants or the ammonia product?

YES

Your choice of small molecule 2.5/5

Have you completed the calculation and included all relevant information?

YES but you forgot to link to the log file again.

Have you added information about MOs and charges on atoms?

YES - the explanation of how the different AOs contribute to each MO was very good. You could have explained the charges in terms of electronegativity. You explained the bonding vs antibonding characters of the MOs well but not how the contribute to the bonds between atoms. For example the LUMO has an antibonding character but it doesn't contribute to the bonding in the molecule as it is unoccupied.

Independence 1/1

If you have finished everything else and have spare time in the lab you could: Check one of your results against the literature, or Do an extra calculation on another small molecule, or Do some deeper analysis on your results so far

you did an extra energy calculation and an extra calculation on S well done!

NH3 Optimisation

Vibration Modes

Atomic Charges

H2 Optimisation

N2 Optimisation

Structure and Reactivity

Haber-Bosch Process

Energy Calculation

Chosen Molecule: SH2

Vibration Modes

Atomic Charges

Energy Calculation

Molecular Orbitals

Marking

Wiki structure and presentation 1/1

NH3 0/1

N2 and H2 0/0.5

Crystal structure comparison 0.5/0.5

Haber-Bosch reaction energy calculation 1/1

Your choice of small molecule 2.5/5

Independence 1/1

NH₃ Optimisation

H₂ Optimisation

N₂ Optimisation

Chosen Molecule: SH₂