NH₃ Molecule

Molecule	NH₃
Calculation Method	RB3LYP
Basis Set	6-31G(d.p)
Final E(RB3LYP) Energy (AU)	-56.55777
RMS Gradient Norm (AU)	4.85 x 10^-6
Point Group	C3v

The table above represents the optimisation settings and values extracted from optimisation for the NH₃ molecule.

NH₃ Molecule Data

NH₃ Bond Length: 1.02Å

NH₃ Bond Angle: 106°

NH₃ Forces and Displacements

Item                      Value     Threshold  Converged? 
Maximum Force            0.000004     0.000450     YES
RMS     Force            0.000004     0.000300     YES 
Maximum Displacement     0.000072     0.001800     YES 
RMS     Displacement     0.000035     0.001200     YES 
Predicted change in Energy=-5.986263D-10 
Optimization completed.   
 -- Stationary point found.

The table above displays values for Maximum and RMS Forces and displacements for NH₃. There is also a threshold column in which the values are compared to the threshold and if the value extracted is lower then the threshold value then the molecule is optimised; the converged column displays a yes.

NH₃ Interactive Image

NH JMol

Link to NH₃ log file

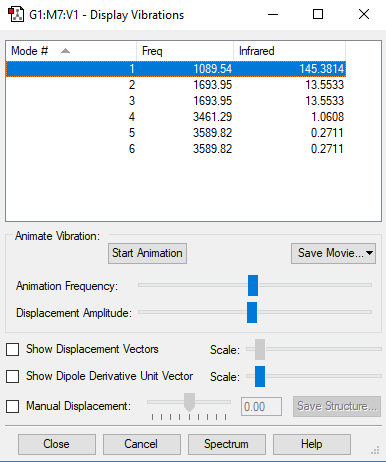
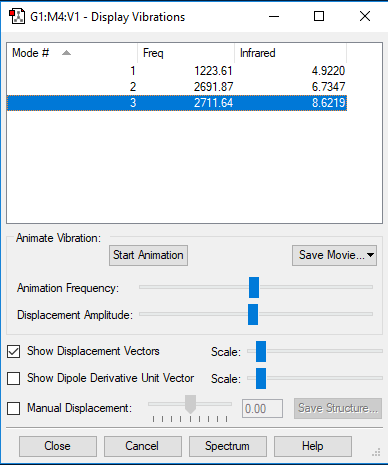
NH₃ Vibration Analysis

The image above displays the different vibrational modes of an NH₃ molecule.

Vibration	1	2	3	4	5	6
Wavenumber (cm^-1)	1090	1694	1694	3461	3590	3590
Infrared Intensity (AU)	145	14	14	1	0	0
Symmetry	A1	E	E	A1	E	E
Snapshot

The table above shows the frequency, infrared intensity, symmetry and a snapshot associated with each vibration of NH₃ where each value is to the nearest integer.

Using the 3N-6 rule you would expect 6 vibration modes to be present in a molecule of NH3. This is because there are 4 atoms in NH3 so N = 4 therefore 3N-6 = 6. There are two sets of two degenerate vibrations, one of these sets are the 1694cm^-1 stretches and the other set are the 3590cm^-1 stretches.
The vibrations at frequencies 1090cm^-1 and 1694cm^-1 are the bending stretches and the vibrations are frequencies 3461cm^-1and 3590cm^-1 are bond stretches.
The vibration at frequency 3461cm^-1 is the most symmetric stretch of them all.
The vibration at frequency 1090cm^-1 (furthest left in the above table) is known as the 'umbrella' vibration.
You would expect to see 2 bands in the spectrum of gaseous Ammonia. These bands would be at frequencies 1090cm^-1 and at 1694cm^-1.

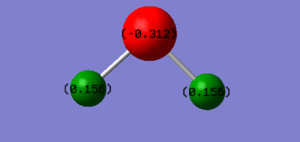
NH₃ Charge Analysis

The charge on the Nitrogen atom is -1.125 and each of the Hydrogen +0.375. This is similar to what you would expect as relatively you expect the Nitrogen to be more negatively charged as it has a higher electronegativity than the 3 Hydrogen's. So the Nitrogen atom pulls electron density towards itself and hence becomes more negatively charged.

N₂ Molecule

Molecule	N₂
Calculation Method	RB3LYP
Basis Set	6-31G(d.p)
Final E(RB3LYP) Energy (AU)	-109.52412
RMS Gradient Norm (AU)	0.00220
Point Group	D*H

The table above represents the optimisation settings and values extracted from optimisation for the N₂molecule.

N₂ Molecule Data

N₂ Bond Length: 1.12Å

N₂ Forces and Displacements

 
 Item                      Value     Threshold  Converged?
 Maximum Force            0.000001     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000000     0.001200     YES
 Predicted change in Energy=-3.401031D-13
 Optimization completed.
    -- Stationary point found.

The table above displays values for Maximum and RMS Forces and displacements for N₂. There is also a threshold column in which the values are compared to the threshold and if the value extracted is lower then the threshold value then the molecule is optimised; the converged column displays a yes.

N₂ Interactive Image

N JMol

Link to N₂ log file

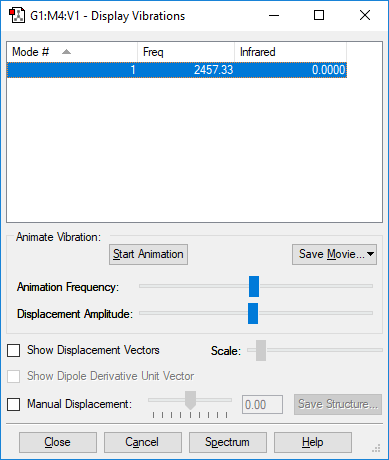
N₂ Vibration Analysis

The image above displays the different vibrational modes of an N₂ molecule.

Vibration	1
Wavenumber (cm_-1)	2457
Intensity (au)	0
Snapshot

The table above shows the frequency, infrared intensity, symmetry and a snapshot associated with each vibration of NH3 where each value is to the nearest integer.

Using the 3N-5 rule you would expect 1 vibration mode to be present in a molecule of N₂. As N = 2 due to 2 atoms in the molecule and hence 3N-5 = 1.
The only vibration at frequency 2457 cm-1 represents a bond stretching frequency.

N₂ Charge Analysis

The charge on both Nitrogen atoms is 0. This is expected as the electronegativity of each atom is equal so they both have an equal and opposite pull on the electron density which means no overall charge.

H₂ Molecule

Molecule	H2
Calculation Method	RB3LYP
Basis Set	6-31G(d.p)
Final E(RB3LYP) Energy (AU)	-1.17854
RMS Gradient Norm (AU)	1.1 x 10-7
Point Group	D*H

The table above represents the optimisation settings and values extracted from optimisation for the H₂molecule.

H₂ Molecule Data

H₂ Bond Length: 0.74Å

H₂ Forces and Displacements

 Item                      Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000001     0.001200     YES
 Predicted change in Energy=-1.164080D-13
 Optimization completed.
    -- Stationary point found.

The table above displays values for Maximum and RMS Forces and displacements for H₂. There is also a threshold column in which the values are compared to the threshold and if the value extracted is lower then the threshold value then the molecule is optimised; the converged column displays a yes.

H₂ Interactive Image

H JMol

Link to H₂ log file

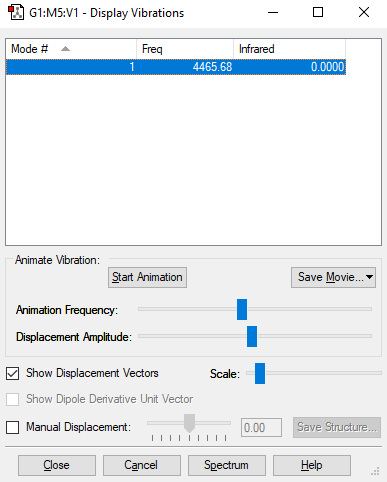
H₂ Vibrational Analysis

The image above displays the different vibrational modes of an H₂ molecule.

Vibration	1
Wavenumber (cm-1)	4466
Intensity (AU)	0
Snapshot

The table above shows the frequency, infrared intensity, symmetry and a snapshot associated with each vibration of H₂ where each value is to the nearest integer.

Using the 3N-5 rule you would expect 1 vibration mode to be present in a molecule of H₂. As N = 2 due to 2 atoms in the molecule and hence 3N-5 = 1.
The only vibration at frequency 4466cm^-1 represents a bond stretching frequency.

H₂ Charge Analysis

The charge on both Hydrogen atoms is 0. This is expected as the electronegativity of each atom is equal so they both have an equal and opposite pull on the electron density which means no overall charge.

H₂ Transition Metal Complex

Unique identifier code: BIDQUB

Link to Transition Metal Complex:[[1]]

H₂ Bond length in Complex= 0.912Å ^[1]

H₂ Bond Length in Diatomic: 0.74Å

Why is there a difference in bond lengths?

There is a difference in bond lengths as in diatomic Hydrogen the electron density of both atoms is shared between only the Hydrogen atoms. When a Ruthenium atom bonds with the Hydrogen it pulls the electron density towards itself and thus reduces the bond density. This effect is even larger since the Ruthenium atom bonds to both Hydrogen atoms.

Why is there a difference between experimental and computational distances.

There is a difference as a RB3LYP calculation method was used and this only uses a few parameters so a calculation method with more parameters that can be changed and set would provide distances to a higher degree of accuracy. On the other hand if the best equipment known is not used then it produces less accurate distances.

Haber Bosch Process

	Energy (au)
E(NH₃)	-56.55777
2*E(NH₃)	-113.11554
E(N₂)	-109.52412
E(H₂)	-1.17854
3*E(H₂)	-3.53562
ΔE=2E(NH₃)-[E(N₂)+3E(₂)]	-0.05579

ΔE = -146.5kJmol-1.

The above table displays values computed through optimisation in Gaussian software. The values are used to predict the energy of the Haber-Bosch process. The ammonia product is more stable as it is lower in energy compared to the gaseous reactants.

Carbon Monoxide

Molecule	Carbon Monoxide
Calculation Type	RB3LYP
Basis Set	-6-31G(d.p)
Final E(RB3LYP) Energy (au)	-113.30945
RMS Gradient Norm	2.02 x 10-6
Point Group	C*V

The table above represents the optimisation settings and values extracted from optimisation for the CO molecule.

CO Molecule Data

CO Bond Length: 1.14Å

CO Forces and Displacements

 
Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000001     0.001800     YES
 RMS     Displacement     0.000002     0.001200     YES
 Predicted change in Energy=-4.844651D-12
 Optimization completed.
    -- Stationary point found.

The table above displays values for Maximum and RMS Forces and displacements for CO. There is also a threshold column in which the values are compared to the threshold and if the value extracted is lower then the threshold value then the molecule is optimised; the converged column displays a yes.

CO Interactive Image

N JMol

Link to CO log file

CO Vibration Analysis

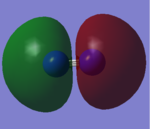
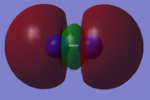
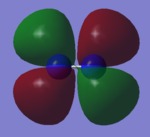
The image above displays the different vibrational modes of a CO molecule.

Vibration	1
Wavenumber (cm-1)	2209
Intensity (AU)	68
Snapshot

The table above shows the frequency, infrared intensity, symmetry and a snapshot associated with each vibration of CO where each value is to the nearest integer.

Using the 3N-5 rule you would expect 1 vibration mode to be present in a molecule of H₂. As N = 2 due to 2 atoms in the molecule and hence 3N-5 = 1.
The only vibration at frequency 2209cm-1 represents a bond stretching frequency.

CO Vibration Analysis

The charge on Oxygen is -0.506 and the charge on Carbon is +0.506 . This is expected as the electronegativity of Oxygen is much greater than Carbon so the has have a much stronger pull on the electron density hence, Oxygen is more negative.

CO Molecular Orbitals

Molecular Orbitals	1	2	3	4	5
Type of Molecular Orbital	σ_1s	σ*_2s	π_2p	σ_2p	π*_2p
Energy (au)	-14.44676(Very deep in energy)	-0.55342 (high in energy and higher in energy than 1s)	-0.46240(high in energy and higher in energy than 2s)	-0.42688(high in energy and higher in energy than 2s and previous 2p)	-0.02412(High in energy relative to the other orbitals)
Atomic Orbitals Contributing to Molecular Orbital	Two 1s Orbitals	Two 2s Orbitals	Two 2p Orbitals	Two 2p Orbitals	Two 2p Orbitals
Occupancy of Molecular Orbital	Occupied	Occupied	Occupied	Occupied	Unoccupied
Snapshot
Description of Molecular Orbitals	This molecular orbital is made from 1s atomic orbitals so is very deep in energy as the MO has very little effect on the bonding.	This molecular orbital is relatively high in energy and has little effect on the bonding but more of an effect than the 1s σ MO.	This moleucular orbital is high in energy and has more of an effect on the bonding as the AO's are large so a stronger overlap is present.	This molecular orbital is high in energy and is the HOMO. Has a very significant effect on the bonding as the AO's are very large so a very strong overlap is present.	This MO is the LUMO. Does not have a significant effect on bonding as it is unoccupied.

H₂S- Independence Mark

Molecule	H₂S
Calculation Method	RB3LYP
Basis Set	6-31G(d.p)
Final E(RB3LYP) Energy (au)	--399.39162
RMS Gradient Norm (au)	1.2068 x 10^-4
Point Group	C2V

The table above represents the optimisation settings and values extracted from optimisation for the H₂S molecule.

H₂S Molecule Data

H₂S Bond Length: 1.35Å

H₂S Bond Angle: 93°

H₂S Forces and Displacements

 Item                      Value     Threshold  Converged?
 Maximum Force            0.000175     0.000450     YES
 RMS     Force            0.000145     0.000300     YES
 Maximum Displacement     0.000472     0.001800     YES
 RMS     Displacement     0.000386     0.001200     YES
 Predicted change in Energy=-1.208488D-07
 Optimization completed.
    -- Stationary point found.

The table above displays values for Maximum and RMS Forces and displacements for H₂S. There is also a threshold column in which the values are compared to the threshold and if the value extracted is lower then the threshold value then the molecule is optimised; the converged column displays a yes.

H₂S Interactive Image

N JMol

Link to H₂S log file

H₂S Vibration Analysis

The image above displays the different vibrational modes of an H₂S molecule.

Vibration	1	2	3
Wavenumber (cm^-1)	1224	2692	2712
Infrared Intensity (au)	5	7	9
Symmetry	A1	A1	B2
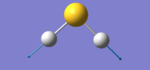
Snapshot

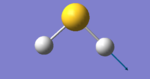
The table above shows the frequency, infrared intensity, symmetry and a snapshot associated with each vibration of H₂S where each value is to the nearest integer.

Using the 3N-6 rule you would expect 3 vibration modes to be present in a molecule of H₂S. This is because there are 4 atoms in H₂S so N = 3 therefore 3N-6 = 3.
The vibration at frequency 1224cm^-1 is a bending stretch and the vibrations at frequencies 2692cm^-1and 2712cm^-1 are bond stretches.

H₂S Charge Analysis

The charge on the Sulfur atom is -0.312 and each of the Hydrogen +0.156. This is as expected as the Sulfur is more electronegative than the hydrogen atoms and so pulls the electron density towards itself making Sulfur more negative.

References

↑ (1)D.Sellmann, A.Hille, F.W.Heinemann, M.Moll, M.Reiher, B.A.Hess, W.Bauer CCDC 229678: Experimental Crystal Structure Determination, 2005, DOI: 10.5517/cc7pzzv

Marking

Note: All grades and comments are provisional and subject to change until your grades are officially returned via blackboard. Please do not contact anyone about anything to do with the marking of this lab until you have received your grade from blackboard.

Comment: You wiki shows you have a good level of understanding but you analysed the wrong MOs in the section worth most of the marks.

Wiki structure and presentation 0.5/1

Is your wiki page clear and easy to follow, with consistent formatting?

YES

Do you effectively use tables, figures and subheadings to communicate your work?

YES - however, all your mols are just labelled 'mol' which is not informative at all.

NH3 1/1

Have you completed the calculation and given a link to the file?

YES

Have you included summary and item tables in your wiki?

YES

Have you included a 3d jmol file or an image of the finished structure?

YES

Have you included the bond lengths and angles asked for?

YES

Have you included the “display vibrations” table?

YES

Have you added a table to your wiki listing the wavenumber and intensity of each vibration?

YES

Did you do the optional extra of adding images of the vibrations?

YES

Have you included answers to the questions about vibrations and charges in the lab script?

YES

N2 and H2 0.5/0.5

Have you completed the calculations and included all relevant information? (summary, item table, structural information, jmol image, vibrations and charges)

YES

Crystal structure comparison 0.5/0.5

Have you included a link to a structure from the CCDC that includes a coordinated N2 or H2 molecule?

YES

Have you compared your optimised bond distance to the crystal structure bond distance?

YES

Haber-Bosch reaction energy calculation 1/1

Have you correctly calculated the energies asked for? ΔE=2*E(NH3)-[E(N2)+3*E(H2)]

YES

Have you reported your answers to the correct number of decimal places?

YES

Do your energies have the correct +/- sign?

YES

Have you answered the question, Identify which is more stable the gaseous reactants or the ammonia product?

YES

Your choice of small molecule 1/5

Have you completed the calculation and included all relevant information?

YES

Have you added information about MOs and charges on atoms?

Most of the marks are rewarded for the MO analysis. In this section you claimed to analyse CO but the displayed MOs are the ones of N2!

Independence 1/1

If you have finished everything else and have spare time in the lab you could:

Check one of your results against the literature, or

Do an extra calculation on another small molecule, or

YES

Do some deeper analysis on your results so far

[distance-1] (1)D.Sellmann, A.Hille, F.W.Heinemann, M.Moll, M.Reiher, B.A.Hess, W.Bauer CCDC 229678: Experimental Crystal Structure Determination, 2005, DOI: 10.5517/cc7pzzv

[1]

NH3 Molecule

NH3 Molecule Data

NH3 Forces and Displacements

NH3 Interactive Image

NH3 Vibration Analysis

NH3 Charge Analysis

N2 Molecule

N2 Molecule Data

N2 Forces and Displacements

N2 Interactive Image

N2 Vibration Analysis

N2 Charge Analysis

H2 Molecule

H2 Molecule Data

H2 Forces and Displacements

H2 Interactive Image

H2 Vibrational Analysis

H2 Charge Analysis

H2 Transition Metal Complex

Haber Bosch Process

Carbon Monoxide

CO Molecule Data

CO Forces and Displacements

CO Interactive Image

CO Vibration Analysis

CO Vibration Analysis

CO Molecular Orbitals

H2S- Independence Mark

H2S Molecule Data

H2S Forces and Displacements

H2S Interactive Image

H2S Vibration Analysis

H2S Charge Analysis

References

Marking

Wiki structure and presentation 0.5/1

NH3 1/1

N2 and H2 0.5/0.5

Crystal structure comparison 0.5/0.5

Haber-Bosch reaction energy calculation 1/1

Your choice of small molecule 1/5

Independence 1/1

NH₃ Molecule

NH₃ Molecule Data

NH₃ Forces and Displacements

NH₃ Interactive Image

NH₃ Vibration Analysis

NH₃ Charge Analysis

N₂ Molecule

N₂ Molecule Data

N₂ Forces and Displacements

N₂ Interactive Image

N₂ Vibration Analysis

N₂ Charge Analysis

H₂ Molecule

H₂ Molecule Data

H₂ Forces and Displacements

H₂ Interactive Image

H₂ Vibrational Analysis

H₂ Charge Analysis

H₂ Transition Metal Complex

H₂S- Independence Mark

H₂S Molecule Data

H₂S Forces and Displacements

H₂S Interactive Image

H₂S Vibration Analysis

H₂S Charge Analysis