Rep:Mod:HF300

The Cope Rearrangement

The Cope rearrangement involves the [3,3]-sigmatropic rearrangement of 1,5-dienes and its mechanism has been studied extensively over the years, where the reaction can be considered to proceed via either a'chair' or a 'boat' transition state structures. In this part of the physical computational study, the Cope rearrangement of 1,5-hexadiene was investigated by researching into the energy differences between the different transition states. Gaussian was utilised to calculate the optimised energy minimum on the potential energy surface (PES) in order to calculate the activation energy as well as explore the reaction pathway by following the minimum energy pathway from a particular transition state down to a local minimum.

The Cope Rearrangement

Optimising the Reactants and Products

Preliminary Optimisation of 1,5-hexadiene using Hartree-Fock/3-21G

Gaussian was used to optimise four different conformers of 1,5-hexadiene at the Hartree-Fock/3-21G (HF/3-21G) level of theory. The first is an anti-periplanar (app) conformer of 1,5-hexadiene. The optimised structure can be seen to have a minimised energy value of -231.69260 a.u. and C₂ point group assignment. After comparison with the table of conformers given in Appendix 1, this app conformer was determined to be anti1.

In the second optimisation procedure, a conformer with a 'gauche' linkage for the central four carbons was drawn by changing the dihedral angle of the last app structure from 180^o to 60^o. This conformer was expected to have higher energy as the gauche conformation generally introduces more steric hinderance and thus an increase in energy might also be expected. After optimisation, the energy of the gauche conformer was determined to be -231.69153 a.u. and its point group was shown to be C₂, which was resolved to be gauche4.

As expected the energy of the app conformer is slightly lower compared to gauche 1,5-Hexadiene. A few more conformers are potential candidates for having the lowest energy and therefore, further calculations were performed in order to determined the one with the lowest energy. Another app conformer, the anti2 conformer, was successfully reproduced energy values of -231.69254 a.u. with a C_i point group.

However, this was not the conformer with the lowest energy. A gauche conformer with methylene groups on the end pointing directly away from each other and thus likely to have the lowest energy values, was calculated to have a minimised energy value of -231.69266 a.u. and a point group of C₁. After comparing with the conformers provided, it was confirmed to be the conformer with the lowest energy.

It is surprising that a gauche conformer, rather than an anti-periplanar conformer, had the lowest energy. It is perhaps due to the particular structural geometry giving access to enhanced orbital overlap offering additional stabilisation.

The four HF/3-21G optimised conformers and their respective energies as well as their point group are listed in their respective summary tables below.

Conformer	Anti1	Anti2	Gauche3	Gauche4
Image
File Name	CR_anti1_opt_3-21g	CR_anti2_opt_3-21g	CR_Gauche3_opt_3-21g	CR_Gauche4_opt_3-21g
File Type	.log	.log	.log	.log
Calculation Type	FOPT	FOPT	FOPT	FOPT
Calculation Method	RHF	RHF	RHF	RHF
Basis Set	3-21G	3-21G	3-21G	3-21G
Charge	0	0	0	0
Spin	Singlet	Singlet	Singlet	Singlet
Energy (a.u.)	-231.69260	-231.69253	-231.69266	-231.69153
RMS Gradient Norm	0.00002114	0.00001823	0.00000995	0.00000165
Dipole Moment	0.2023 D	0.0000 D	0.3404 D	0.1281 D
Point Group	C2	Ci	C1	C2
Computational Time	1 min 40.6 sec	59.7 sec	1 min 25.8 sec	1 min 21.5 sec
Log File	[Anti1]	[Anti2]	[Gauche3]	[Gauche4]

It is important to ascertain whether the optimisation are successful. Examination of the RMS Gradient Norm suggests that minimum points has been found as the values for all the forms are extremely low. In addition, from the item tables for the conformers below, it can be seen that the calculation have all converged. Moreover, frequency calculations were also preformed on the conformers in order to make certain the optimised structures are indeed minimum energy structures and not a transition state. The fact that the low frequencies are all relatively small (within the limits of ±15 cm^-1) and that no imaginary frequencies were founds indicates that the optimisations performed have found the minimum energy structure.

Conformer	Item Table	Low Frequencies
Anti1	Item Value Threshold Converged? Maximum Force 0.000041 0.000450 YES RMS Force 0.000016 0.000300 YES Maximum Displacement 0.001575 0.001800 YES RMS Displacement 0.000648 0.001200 YES Predicted change in Energy=-6.980175D-08 Optimization completed. -- Stationary point found.	Low frequencies --- -7.1742 -2.0832 0.0003 0.0003 0.0018 1.7470 Low frequencies --- 76.2750 97.9343 109.1552
Anti2	Item Value Threshold Converged? Maximum Force 0.000041 0.000450 YES RMS Force 0.000016 0.000300 YES Maximum Displacement 0.000403 0.001800 YES RMS Displacement 0.000145 0.001200 YES Predicted change in Energy=-5.594855D-08 Optimization completed. -- Stationary point found.	Low frequencies --- -3.5230 -0.0003 0.0004 0.0009 0.7973 6.9134 Low frequencies --- 71.8124 85.7668 116.5178
Gauche3	Item Value Threshold Converged? Maximum Force 0.000041 0.000450 YES RMS Force 0.000008 0.000300 YES Maximum Displacement 0.001603 0.001800 YES RMS Displacement 0.000395 0.001200 YES Predicted change in Energy=-2.297596D-08 Optimization completed. -- Stationary point found.	Low frequencies --- -2.0567 -0.0004 -0.0004 0.0004 1.4423 2.8682 Low frequencies --- 74.5873 105.0382 130.5675
Gauche4	Item Value Threshold Converged? Maximum Force 0.000012 0.000450 YES RMS Force 0.000003 0.000300 YES Maximum Displacement 0.000190 0.001800 YES RMS Displacement 0.000056 0.001200 YES Predicted change in Energy=-1.078330D-09 Optimization completed. -- Stationary point found.	Low frequencies --- -2.0660 -0.7638 -0.0154 0.0023 0.0035 0.2523 Low frequencies --- 65.5198 68.6388 147.3235

Optimisation and Frequency Analysis of Anti2 Conformer using B3LYP/6-31G*

The anti2 conformer was reoptimised at the B3LYP/6-31G* level. The obtained minimised energy was -234.61171046 a.u. and the point group remained as C_i. From the results it can be concluded that the optimisation was again successful as the RSM Gradient Norm is very low and the calculations have all converged. The summary table of results and the item table can be seen below.

Summary Table

Property	Value
File Name	CR_anti2_optfreq_621g_d
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d)
Charge	0
Spin	Singlet
Energy	-234.61171046 a.u.
RMS Gradient Norm	0.00001225 a.u.
Dipole Moment	0.00 D
Point Group	CS
Computational Time	3 min 13.7 sec
Log File	[Anti2 (DFT optimised)]

Item Table
Item Value Threshold Converged? Maximum Force 0.000014 0.000450 YES RMS Force 0.000006 0.000300 YES Maximum Displacement 0.000231 0.001800 YES RMS Displacement 0.000079 0.001200 YES Predicted change in Energy=-1.386780D-08 Optimization completed. -- Stationary point found.

Upon comparing the optimised structures between using the lower HF/3-21G level of theory and the higher B3LYP/6-31G*, it can be seen that not much has changed with regards to the geometry of the molecule. However, there are subtle changes with regards to bond distances and bond angles. The result can be seen below.

Bond Length	Hartree-Fock	DFT	Bond Angle	Hartree-Fock	DFT
C(1)=C(2)	1.32Å	1.33Å	C(1)-C(2)-C(3)	124.8o	125.3o
C(2)-C(3)	1.51Å	1.50Å	C(2)-C(3)-C(4)	111.3o	112.7o
C(3)-C(4)	1.55Å	1.55Å	C(3)-C(4)-C(5)	111.3o	112.7o
C(4)-C(5)	1.51Å	1.50Å	C(4)-C(5)-C(6)	124.8o	125.3o
C(5)=C(6)	1.32Å	1.33Å

It is apparent that for molecules of this complexity, the two different levels of calculation theory produces roughly the same molecule. It is worth mentioning that there are significant differences between the energies of these optimised molecules. This is due to the fact that different theories have different assumptions, which leads to energy values in different 'regions'. In other words, the energies produces from two different methods can't be compared and energy comparisons should only be done for optimised molecules using the same theory.

A frequency analysis calculation using the B3LYP/6-31G* level of theory was also carried out. The results can be seen below.

 Low frequencies ---  -10.8537   -0.0009   -0.0008   -0.0005    5.2386   16.1208
 Low frequencies ---   72.4888   80.3727  121.7046

The first line represents the 'external vibrations', i.e. the translational and rotational modes of the molecule. The better the method employed, the closer to zero these values will be. The second line represents the lowest 'real' vibrational frequencies. None of these are negative, which indicates that the optimisation has indeed reached a minimum.

In addition, a list of four important energies can be seen under the Thermochemistry section. The first is the sum of electronic and zero-point energies, which correspond to the potential energy at 0K and the zero-point energy (E = E_elec+ZPE). The second is the energy contribution from the translational, rotational and vibratiinal energy modoes at 298.15K and 1 atm (E = E + E_trans + E_rot + E_vib). The third of which, includes correction for room temperature (H = E + RT ) and the last includes contribution from entropy (G = H - TS). The results for these energies can be seen in the table below.

List of Energies at 298.15K

Energies	Value (a.u.)
Sum of electronic and zero-point Energies	-234.469226
Sum of electronic and thermal Energies	-234.461871
Sum of electronic and thermal Enthalpies	-234.460926
Sum of electronic and thermal Free Energies	-234.500830

The same frequency analysis calculation was re-performed with the temperature set to near 0K (calculations could not be set to 0K as gaussian appears to ignore this setting and performs the calculation at 298.15K). The keyword temperature=0.001K was used to set the conditions of the frequency analysis to near 0K. The results for the different energies are listed below.

List of Energies at 0.001K

Energies	Value (a.u.)
Sum of electronic and zero-point Energies	-234.469226
Sum of electronic and thermal Energies	-234.469226
Sum of electronic and thermal Enthalpies	-234.469226
Sum of electronic and thermal Free Energies	-234.469226

As expected, at near 0K, no further energy contributions exists on top of the intrinsic electronic energy at 0K and zero point energy. This is indicated by all the energies being the same as the 'sum of electronic and zero-point energies'.

Optimising the "Chair" and "Boat" Transition States

Two possible transition states exist for the Cope rearrangement of 1,5-hexadiene: the chair form and boat form. The transition states was computed using three different methods. The first of which is the 'Hessian method', where the force constants were computed at the beginning of the calculation. The second method entails two separate steps and using the 'redundant coordinate editor'. The last method involves the use of QST2 function.

Ally fragement

An ally fragments (CH₂CHCH₂), was optimised using the HF/3-21G method and basis set. After optimisation, the structure achieved an expected geometry, where all the bonds were equal distances (1.39Å) and a C-C-C bond angle of (124.3°). The results including the summary table can be seen below. This structure, which correspond to half the transition state, was used as the building block for locating the chair transition state.

Summary Table

Property	Value
File Name	TC_CH2CHCH2_opt_321g
File Type	.log
Calculation Type	FOPT
Calculation Method	UHF
Basis Set	3-21G
Charge	0
Spin	Doublet
Energy	-115.82303991 a.u.
RMS Gradient Norm	0.00009674 a.u.
Dipole Moment	0.0293 D
Point Group	C1
Computational Time	24.1 sec
Log File	[Ally Fragment]

Item table	Item Value Threshold Converged? Maximum Force 0.000160 0.000450 YES RMS Force 0.000056 0.000300 YES Maximum Displacement 0.000711 0.001800 YES RMS Displacement 0.000290 0.001200 YES Predicted change in Energy=-1.860750D-07 Optimization completed. -- Stationary point found.
Low Frequencies	Low frequencies --- -7.2874 0.0008 0.0010 0.0011 2.4592 15.2102 Low frequencies --- 474.7648 555.7906 579.7916

Chair Transition State

'Guess structure' for the chair transitions state

In order to obtain the chair transition state structure, a guess structure was constructed using two copies of the pre-optimised ally fragment and manually rotating and arranging the groups until a chair-like structure was obtained. The terminal allyl groups were placed approximately 2.20Å apart. The 'Hessian' method and the 'Freeze Coordinate' method were both used in attempt to locate the chair transition state. It was found that both methods arrived at the same transition state, with one imaginary frequency corresponding to the Cope rearrangement.

Animation of the imaginary frequency corresponding to the Cope rearrangement

Hessian Method

The 'Hessian method' was first used in attempt to obtain the chair transition state. A gaussian calculation was setup for a Opt+Freq job and optimised to a TS(berny) with force constants calculated once using HF/3-21G. In addition, the keyword opt=noeigen was added to prevent the calculation from ending in the case of imaginary frequencies. The results can be seen below.

Summary Table

Property	Value	Image
File Name	chair_optfreq_berny_part_b	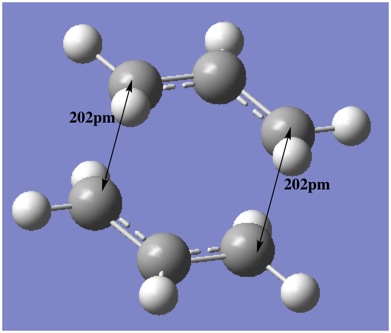The Chair transition state as located using the 'Hessian' method
File Type	.log
Calculation Type	FREQ
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	Singlet
Energy	-231.61932225 a.u.
RMS Gradient Norm	0.00004441 a.u.
Imaginary Freq	1 (818 cm-1)
Dipole Moment	0.0007 D
Point Group	C1
Computational Time	20.9 sec
Log File	[Chair TS using Hessian Method]
Item Table	Item Value Threshold Converged? Maximum Force 0.000079 0.000450 YES RMS Force 0.000020 0.000300 YES Maximum Displacement 0.001767 0.001800 YES RMS Displacement 0.000490 0.001200 YES Predicted change in Energy=-2.251574D-07 Optimization completed. -- Stationary point found.

The opt+freq operation afforded the optimised structure with terminal groups being a distance of 2.02Å apart. The transition state can be seen and by animating the vibrational mode with the imaginary frequency of -818cm^-1, it can be seen that the motion does resemble the Cope rearrangement, where the asymmetrical motion indicates a chain of six carbons forming and breaking.

Frozen Coordinate Method

A different method involving two steps was used to locate the chair transition state. The optimised allyl fragments was again used in a guess structure for the transition state. The end pairs of carbon atoms that were destined for forming and breaking bonds were then edited using the 'Redundant Coordinate Editor', where they were 'frozen' by editing the option and selecting 'Bond' and 'Freeze Coordinate'. The structure was then set for optimisation. This step allows parts of the structure that are not frozen to be optimised.

The second step in this method for locating the transition state involves performing an opt + freq operation for optimising to a transition state on the previously frozen bonds by first selecting the options for 'bond' and 'Derivative' in the 'Reduction Coordinate Editor' and running the calculation.

Summary Table

Property	Value	Image
File Name	chair_optfreq_berny_part_d	The Chair transition state as located using the 'Freeze Coordinate' method
File Type	.log
Calculation Type	FREQ
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	Singlet
Energy	-231.61932197 a.u.
RMS Gradient Norm	0.00012842 a.u.
Imaginary Freq	1 (-818 cm-1)
Dipole Moment	0.0004 D
Point Group	C1
Computational Time	21.2 sec
Log File	[Chair TS using Freeze Coordinate Method]
Item Table	Item Value Threshold Converged? Maximum Force 0.000081 0.000450 YES RMS Force 0.000021 0.000300 YES Maximum Displacement 0.001358 0.001800 YES RMS Displacement 0.000424 0.001200 YES Predicted change in Energy=-1.436256D-07 Optimization completed. -- Stationary point found.

The output produced the correct transition state, as confirmed by examining the geometry (separation: 2.02Å and C-C-C bond angle of 120.5°) and the imaginary vibrational mode (818 cm^-1.)

It can be seen that the two methods resulted in very similar transition state structures. This should be expected, as although the methods takes different routes, both are trying to locate the same transition state. Therefore, it is convenient, both as a check for whether the transition state located is indeed the correct structure and as alternatively for if one method fails to calculate for any reason.

Boat Transition State

The optimisation to transition state(QST2) method was used to locate the boat-like transition state, where gaussian attempts to obtain the 'mixed middle' structure from the input of the reactants and the product. The B3LYP/6-31G optimised 1,5-hexadiene was added to two different 'frames' in a molecule window. The molecules were numbered and arranged as to present mirror images. The calculation was set up for optimisation to a transition state (QST2).

setup for locating the boat transition state (reactant on the left and product on the right)

The calculation however crashed and that a modification to the geometry of the structures were needed. The central C-C-C-C dihedral angle was set to 0° and the C-C-C angles on both sides were set to 100°. The same calculation was successfully ran.

angle altered setup for locating the boat transition state (reactant on the left and product on the right)

The results showed a boat-like transition state with separation of 2.14Å, slightly larger than its chair-like counterpart. This is likely due to the increased steric effects intrinsic to the boat conformation. The imaginary frequency, -840°, indicates the correct transition structure when the animation of the vibration was examined. In other words, the vibration mode corresponds to the Cope rearrangement.

Boat transition state located using the TS(QST2) method

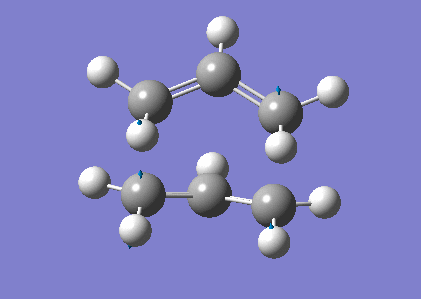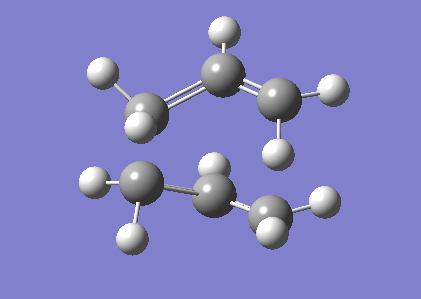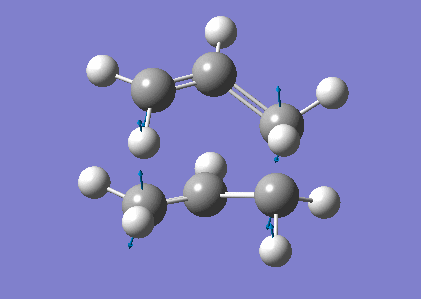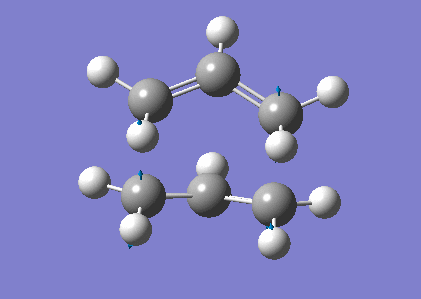
The results of the TS optimisation process is listed in the summary table below.

Summary Table

Property	Value	Image
File Name	chair_optfreq_qst2_part_e_angle_change	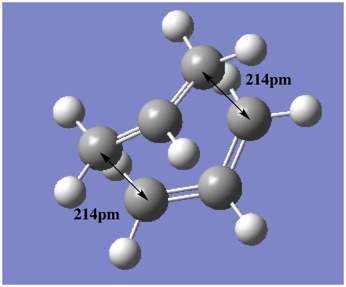The boat transition state as located using the 'TS(QST2)' optimisation method
File Type	.log
Calculation Type	FREQ
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	Singlet
Energy	-231.60280198 a.u.
RMS Gradient Norm	0.00007373 a.u.
Imaginary Freq	1 (-840 cm-1)
Dipole Moment	0.1579 D
Point Group	CS
Computational Time	16.4 sec
Log File	[Boat TS]
Item Table	Item Value Threshold Converged? Maximum Force 0.000091 0.000450 YES RMS Force 0.000031 0.000300 YES Maximum Displacement 0.001645 0.001800 YES RMS Displacement 0.000411 0.001200 YES Predicted change in Energy=-3.457451D-07 Optimization completed. -- Stationary point found.

IRC

The Intrinsic Reaction Coordinate(IRC) method offers another dimension to the investigation of transition states. The IRC performs calculations that results in the display of the minimum energy path from the transition state down to its local minimum on the potential energy surface. This affords the possibility to ascertain which conformers of the 1,5-hexadiene the transition states connects.

The previously HF/3-21G optimised chair transition state was used for the IRC calculation. The calculation direction was set for forwards only (i.e. towards the product), the force constant was set to calculate always. Last but not least, the maximum number of points along the IRC was set to 50.

The IRC path produced can be seen below. The energy profile indicates clearly that the conformation reached a minimum and took 44 steps.

1,5-hexadiene Cope rearrangement via Chair TS

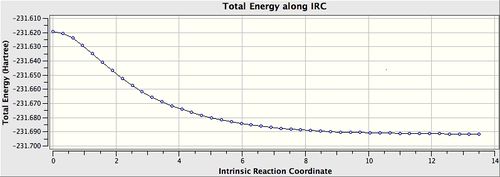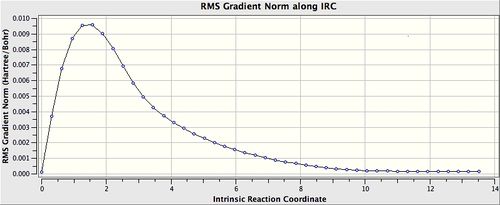
The final structure had an energy value of -231.691577 a.u. Examination of the final structure indicates that it bares close resemblance to the gauche2 conformer. However, the energy value is not that of the said conformer. Therefore, it can be concluded that the structure has not yet reached the minimum geometry. Three different methods had been suggested in attempts to optimise the structure. The first is to perform an optimisation of the final structure. This was done using the HF/3-21G method. The second suggestion was to include more points in the IRC calculation in order for gaussian to compute more points. This method is unlikely to give the properly optimised structure as the initial calculation has already stopped at step 44 even though a total of 50 steps was set. Nevetheless, as a check a second attempt on the IRC calculation with 100 points with force constant calculated once in order to same calculation time. The last suggestion was to perform the IRC with calculation always. This was done again with 100 points. The final results can be seen in the IRC calculation correction results table below.

IRC calculation correction results

Method	1) Optimisation of final structure	2) Increase number of steps	3) Set Force constant to calculate always
Final Structure
Final Energy (a.u.)	-231.691667	-231.6888800	-231.69158

Correction to the initial IRC calculation was done properly only with the first method, which was optimisation of the final structure from the IRC. The second and third method did not offer the proper optimised structure. This is expected as the second method fail at having a high enough correction criteria for optimisation. The third gave the same result as the initial IRC calculation as the problem was not lack of calculation points. Therefore, the only method that gave the proper optimised structure was optimising the final structure from the IRC calculation, The IRC afforded the optimised structure as the gauche 2 conformer when the minimised energy value was examined.

Activation Energies

In order to compare the activation energies (energy between the reactants and the transition state) for the reaction paths leading to the chair and boat transition states, a further optimisation of the two transition states to the B3LYP/6-31G level was performed.

Summary Table

Transition State	Chair	Boat
Image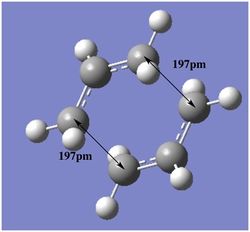
File Name	boat_optfreq_631g_d_part_g	boat_optfreq_631g_d_part_g
File Type	.log	.log
Calculation Type	FREQ	FREQ
Calculation Method	RB3LYP	RB3LYP
Basis Set	6-31G(d)	6-31G(d)
Charge	0	0
Spin	Singlet	Singlet
Energy	-234.55698303 a.u.	-234.55698303 a.u.
RMS Gradient Norm	0.00001198 a.u.	0.00001198 a.u.
Imaginary Freq	1 (-567 cm-1)	1 (-530 cm-1)
Dipole Moment	0.0000 D	0.0613 D
Point Group	C1	CS
Computational Time	6 min 32.9 sec	3 min 49.2 sec
Log File	[Chair TS (DFT opt)]	[Boat TS (DFT opt)]
Item Table	Item Value Threshold Converged? Maximum Force 0.000023 0.000450 YES RMS Force 0.000006 0.000300 YES Maximum Displacement 0.000076 0.001800 YES RMS Displacement 0.000025 0.001200 YES Predicted change in Energy=-3.479941D-09 Optimization completed. -- Stationary point found.	Item Value Threshold Converged? Maximum Force 0.000007 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000054 0.001800 YES RMS Displacement 0.000013 0.001200 YES Predicted change in Energy=-3.631283D-10 Optimization completed. -- Stationary point found.

The re-optimised structures had alterations to the separations between the terminal carbons. For instances, the chair transition state had its terminal carbon of the allyl fragments shortened from 2.02Å to 1.97Å, whereas the boat transition sate had its separation lengthened from 2.14Å to 2.21Å.

In terms of purely electronic energy comparisons, at the HF/3-21G level, the anti2 conformer had an energy value of -231.692535 a.u. chair and boat transition state structures had an energy value of -231.602802 a.u. and -231.619322 a.u. respectively, which correspond to activation energy values of 56.31 kcal/mol and 45.94kcal/mol. On the other hand, at the higher B3LYP/6-31G* level, the energy values altered a significant amount. The anti2 conformer reactant shifted to an energy value of -234.611710 a.u. and the chair and boat conformer energy values also raised to -234.556983 a.u. and -234.543093 a.u. Correspondingly, the activation energies for going to the chair and boat transition state structures are 34.34 kcal/mol and 43.06 kcal/mol respectively. The latter calculation method can be seen to be a better approximation for the Cope rearrangement, as the activation energies calculation is closer to the experimental values provided (chair: 33.5±0.5 kcal/mol and boat: 44.7±2.0 kcal/mol). Full results can be seen in the tabulated data below.

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.619322	-231.466717	-231.461355	-234.556983	-234.414929	-234.409009
Boat TS	-231.602802	-231.450928	-231.445299	-234.543093	-234.402343	-234.396008
Reactant (anti2)	-231.692535	-231.539540	-231.532568	-234.611710	-234.469226	-234.461871

These results agree fairly well with the data given. Below are values for the activation energies.

	HF/3-21G		B3LYP/6-31G*		Expt.**
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.70	44.69	34.07	33.17	33.5 ± 0.5
ΔE (Boat)	55.60	54.76	41.97	41.33	44.7 ± 2.0
** experimental values listed are the values provided on the script.

The tabulated activation energy data for 0K suggests clearly that the B3LYP/6-31G method correlates better with the experiment values, this is expected as this method utilises electron correlations and larger basis set, thereby, producing better results at the expanse of longer calculation time.

The Diels Alder Cycloaddition

The Diels Alder cycloaddition typically entails the reaction between a diene and a dienophile, resulting in the formation of a cyclohexene. The first part investigates a simple reaction between cis-butadiene and ethylene. Thereafter, a more complexed system involving an electron deficient dienophile, maleic anhydride, and the diene, cyclohexa-1,3-diene is researched.

Reaction between cis-butadiene and ethylene

The initial part of this investigation into the Diels Alder cycloaddition shall look into the factors that allow the simple system of cis-Butadiene and ethene to react, including the HOMO and LUMO of the reactants as well as that of the transition state.

Reaction scheme for the Diels Alder cycloaddition between cis-Butadiene and ethene

cis-Butadiene

cis-Butadiene was optimised using the AM1 semi-empirical method which afforded the output structure with reasonable geometry, with C=C bond lengths of 1.33Å, C-C bond length of 1.45Å and a C-C-C bond angle of 125.7°. The results are included in the summary table below.

Summary Table

Property	Value	Image
File Name	TC_cisbutadiene_opt_am1
File Type	.log
Calculation Type	FREQ
Calculation Method	RAM1
Basis Set	ZDO
Charge	0
Spin	Singlet
Energy	0.04879719 a.u.
RMS Gradient Norm	0.00001745 a.u.
Imaginary Freq	1 (818 cm-1)
Dipole Moment	0.0414 D
Point Group	C1
Computational Time	16.1 sec
Log File	[cis-Butadiene]
Item Table	Item Value Threshold Converged? Maximum Force 0.000030 0.000450 YES RMS Force 0.000011 0.000300 YES Maximum Displacement 0.000395 0.001800 YES RMS Displacement 0.000162 0.001200 YES Predicted change in Energy=-9.691186D-09 Optimization completed. -- Stationary point found.

The HOMO and LUMO MOs responsible for the reactivity was also investigated. The MOs can be visualised in the diagram below.

MO	HOMO		LUMO
Visualisation
Symmetry (with respect to the plane)	Asymmetric		Symmetric

The diagrams indicates clearly that the HOMO has one node and is asymmetric about the plane of symmetry. Whereas, the LUMO has two nodes and is symmetric about the plane of symmetry.

Ethene

The second reactant was also optimised using the AM1 semi-empirical method. The optimised structure had the expected geometry of a simple alkene, with a C=C bond length: 1.33Å. The results are listed below.

Summary Table

Property	Value	Image
File Name	TC_ethene_opt_am1
File Type	.log
Calculation Type	FREQ
Calculation Method	RAM1
Basis Set	ZDO
Charge	0
Spin	Singlet
Energy	0.02619024 a.u.
RMS Gradient Norm	0.00000945 a.u.
Dipole Moment	0.0000 D
Point Group	C1
Computational Time	3.4 sec
Log File	[Ethene]
Item Table	Item Value Threshold Converged? Maximum Force 0.000031 0.000450 YES RMS Force 0.000012 0.000300 YES Maximum Displacement 0.000057 0.001800 YES RMS Displacement 0.000037 0.001200 YES Predicted change in Energy=-2.644693D-09 Optimization completed. -- Stationary point found.

The HOMO and LUMO were investigated and the results can be seen below.

MO	HOMO	LUMO
Visualisation
Symmetry (with respect to the plane)	Symmetric	asymmetric

Unlike the cis-butadiene, ethylene's HOMO and LUMO are symmetric and asymmetric about the plane of symmetry respectively. This is an early sign that that reaction is possible duo to the matching of the HOMO and LUMO symmetry between the two reactants. Further examination, particularly of the the transition state, is required in order to ascertain the reactivity of the reaction.

Transition State

The transition state for the reaction between cis-butadiene and ethene was located by first drawing the bicycle[2.2.2]octane, thereafter removing two of the bridging -CH₂ fragments and changing the geometry of one end of the six-member ring, thereby constructing the starting materials. The 'ethylene' end was placed at an approximate guess distance of 2.2 Å away from the 'butadiene end'. After several attempts, the structure was optimised to a TS(Berny), with the frequency also calculated, using the B3LYP/6-31G*, i.e. the transition state was calculated using the 'Hessian method' as outlined above. The calculation converged with the structural geometry below.

Summary Table

Property	Value	Image
File Name	TC_DA_optfreq_berny_b3lyp_631g	The transition state for the Diels Alder reaction between cis-butadiene and ethene
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d)
Charge	0
Spin	Singlet
Energy	-234.54389654 a.u.
RMS Gradient Norm	0.00001719 a.u.
Imaginary Freq	1 (-525 cm-1)
Dipole Moment	0.3950 D
Point Group	C1
Computational Time	9 min 1.5 sec
Log File	[TS for reaction between cis-Butadiene and ethene]
Item Table	Item Value Threshold Converged? Maximum Force 0.000040 0.000450 YES RMS Force 0.000008 0.000300 YES Maximum Displacement 0.000808 0.001800 YES RMS Displacement 0.000223 0.001200 YES Predicted change in Energy=-1.367621D-08 Optimization completed. -- Stationary point found..

The result indicated that the transition state structure has a separation of 2.27 Å between the terminal carbons, which correlates perfectly with the literature value. However, typically, sp³ and sp² C-C bonds have lengths of 1.54 Å and 1.34 Å respectively. Therefore, the 'partially' formed C-C bonds in the transition structure cannot be formally classed as proper bonds. Nevertheless, the normal covalent radius of carbon atoms is 1.70 Å. As the separation between the terminal carbons of the reactants is significantly shorter than the twice the length of the covalent radii (3.40 Å), there is a strong sign of interaction between the components. It is also interesting to observe that the C-C bond that would become the C=C carbon double bond in the cyclohexene product has a bond length of 1.47 Å, which is between the length for a formal C-C single bond and that of a C=C double bond.

From the frequency analysis, it can be seen that a single negative vibrational frequency (-525 cm^-1) has been calculated. Animation of this frequency (below) shows the symmetric, synchronous formation of the two C-C bonds.

Imaginary frequency correlating to the Diels Alder reaction, suggesting the synchronous formation of C-C bonds

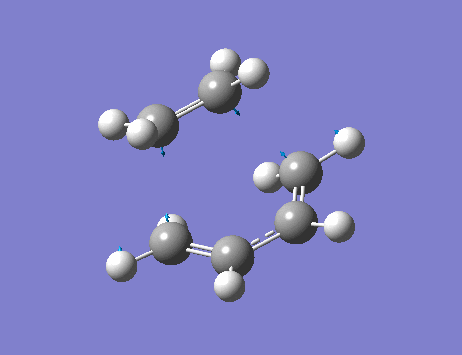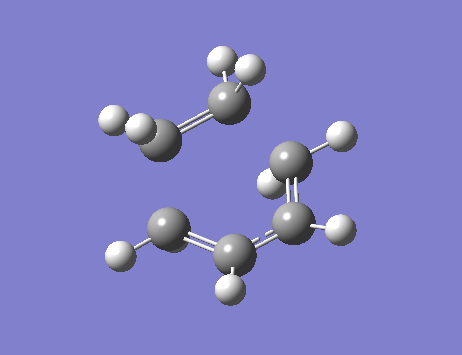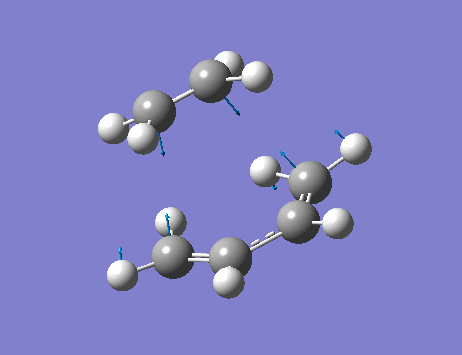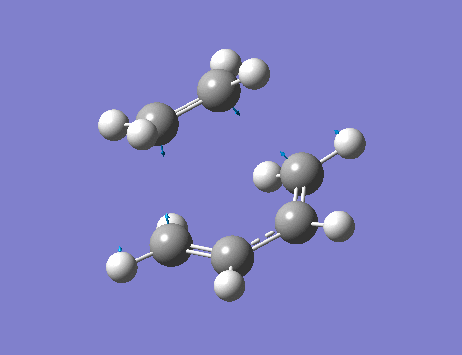
The lowest positive frequency, 136 cm^-1, shows asynchronous vibration of the reactant molecules.

Lowest positive frequency of the transition state structure

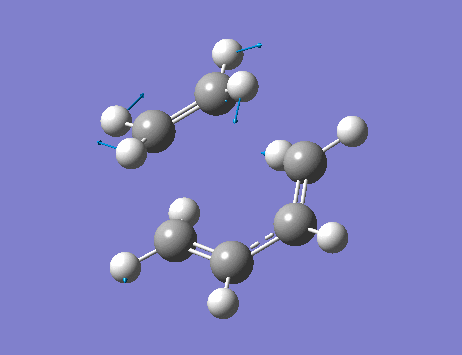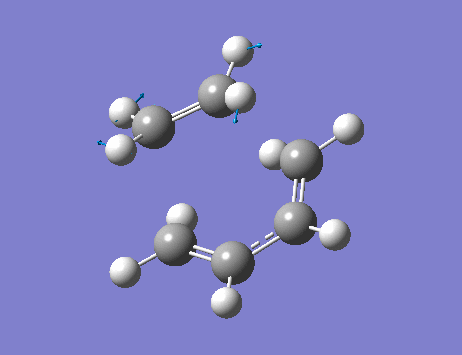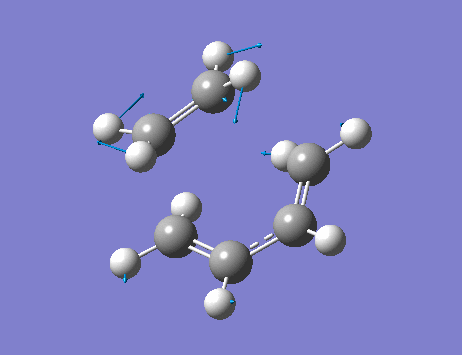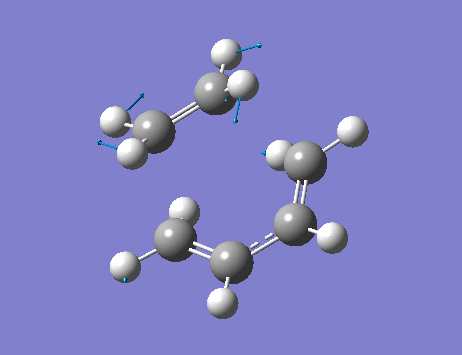
The major difference between the real and imaginary frequency is perhaps the negative sign for the latter. This arises from the fact that the frequency calculation is the second derivative for of the energy found from the optimisation process. The first derivative give the direction in which gaussian should continue to perform its calculation until it reaches a first derivative of close to zero. The second derivative give whether the zero derivative is for a maximum or a minimum. Therefore, it is an indication of whether the optimisation reached is a transition state or a minimised structure for a reactant or product. The former would give a negative frequency (the imaginary frequency) and the latter would give a positive frequency (the real frequency). Further to the idea and understanding of the meaning of the positive and negative sign, one can imagine that for a real and positive frequency, energy is put in in order to excite the molecule to vibrate. Therefore, for an imaginary and negative frequency one can foresee that energy is released for the vibration to reach a minimum on the potential energy surface.

MOs are an important parameter in the investigation of any reaction. The B3LYP method produced the following HOMO and LUMO MOs for the transition state.

MO	HOMO		LUMO
Visualisation
Symmetry (with respect to the plane)	Symmetric		Asymmetric

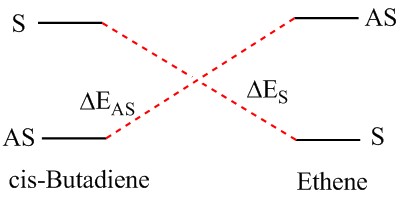
It can be seen that the HOMO of the transition state is clearly symmetric (s) and therefore would be formed by the HOMO of the ethene and the LUMO of the butadiene, which are both symmetric. Furthermore, the symmetry agreement facilitates the symmetry constrain and thereby makes the reaction feasible.

However, because the energy difference between the different levels is very small, there is the possibility of re-ordering of the modes and hence if another method is used for the calculation of MO energies, the case of the HOMO for transision state might be seen as asymmetric (i.e. ΔE_AS is similar to ΔE_S).

HOMO and LUMO of cis-butadiene and ethene

IRC

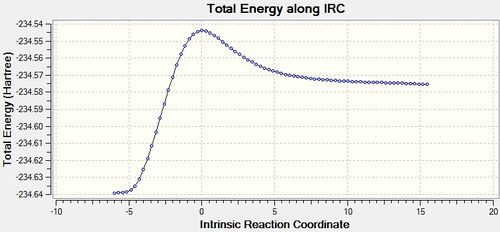
The IRC was also ran for the Diels Alder reaction between cis-butadiene and ethene. The IRC confirms that the transition state obtained is correct.

Please note: gaussian has calculated the reaction in the opposite direction from the norm (i.e. the animation shows what would normally be considered as product to reactants and the graph should be read from right to left, as opposed to the left to right) As gaussian does not 'know' which direction is forwards, they are considered equivalent, whether it is forwards or reverse in the normally chemical sense)

Diels Alder cycloaddition between cis-Butadiene and ethene

Reaction between Maleic Anhydride and Cyclohexa-1,3-diene

The second system studied involves the Diels Alder cycloaddition between the electron deficient dienophile, maleic anhydride and the electron rich diene, cyclohexa-1,3-diene. The reactants were first optimised, thereafter, the transition states were located in order to compare the relative energies and investigate the reaction paths. In this reaction, two possible combinations of the reactants exist, depending on the orientation of them during the formation of the transition state. The combination with the oxygens of the maleic anhydride directly above or below the diene fragment of the cyclohexadiene is known as the endo form, whereas the orientation with the oxygen atoms pointing in opposite directions to the diene is known as the exo form.

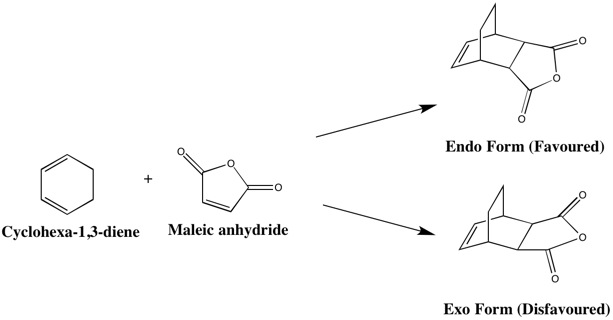
Maleic Anhydride

The dienophile in this reaction is said to be 'electron deficient' due to the electron withdrawing tendency of the oxygens via inductive effects. The structure was optimised along with a frequency calculation performed, using the standard B3LYP/6-31G* theory. The summary from the optimisation can be seen below.

Summary Table

Property	Value	Image
File Name	TC_maleic_anhydride_opt_b3lyp_631g_d
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d)
Charge	0
Spin	Singlet
Energy	-379.28953546 a.u.
RMS Gradient Norm	0.00000056 a.u.
Dipole Moment	4.0712D
Point Group	C1
Computational Time	29 min 45.4 sec
Log File	[maleic anhydride]
Item Table	Item Value Threshold Converged? Maximum Force 0.000001 0.000015 YES RMS Force 0.000000 0.000010 YES Maximum Displacement 0.000004 0.000060 YES RMS Displacement 0.000001 0.000040 YES Predicted change in Energy=-7.112511D-12 Optimization completed. -- Stationary point found.

The MOs are important quantities for investigating the reactivity. The HF/6-31G* method was used to generate the MOs as due to intrinsic assumptions of different method that gaussian uses, certain methods such as DFT would create incorrect results. Upon investigating MOs of the maleic anhydride, it can be seen that the HOMO is symmetric, whereas the LUMO is asymmetric. These orbitals are important for the Diels Alder reaction and visualisation of these MOs can be seen below.

Maleic anhydride MOs
HOMO	LUMO
Symmetric	Asymmetric

Cyclohexa-1,3-diene

THe electron rich diene, cyclohexa-1,3-diene undergone the opt+freq calculation using the B3LYP/6-31G* method and basis set successfully, with the following summary table results

Summary Table

Property	Value	Image
File Name	TC_cyclohexadiene_opt_b3lyp_631g_d
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d)
Charge	0
Spin	Singlet
Energy	-233.41891187 a.u.
RMS Gradient Norm	0.00000092 a.u.
Dipole Moment	0.3776D
Point Group	C1
Computational Time	29 min 45.4 sec
Log File	[cyclohexa-1,3-diene]
Item Table	Item Value Threshold Converged? Maximum Force 0.000001 0.000015 YES RMS Force 0.000000 0.000010 YES Maximum Displacement 0.000006 0.000060 YES RMS Displacement 0.000002 0.000040 YES Predicted change in Energy=-7.015449D-12 Optimization completed. -- Stationary point found..

The MOs were calculated using the HF/6-31G* due to better assumptions with regards to MO generation. The visualisation below indicates that the relatively speaking,HOMO is asymmetric and the LUMO is symmetric.

Cyclohexa-1,3-diene MOs
HOMO	LUMO
Asymmetric	Symmetric

Exo & Endo Transition States

Both the exo and the endo transition state structures were located using the B3LYP/6-31G* method and basis set. The 'Hessian method' was again chosen, where the optimisation was set to TS(Berny) and force constants calculated once, along with the keywords opt=tight opt=noeigen int=ultrafine scf=conver=9 inputted in order to obtain the best possible strucutres. In the guess structure, the nearest distance between the two reactants was set to approx. 2.15 Å and the reactants had their appropriate orientation setup (i.e. the endo and exo had the oxygen groups of the dienophile pointing towards and away from the C=C double bonds of the diene respectively). The results can be seen below.

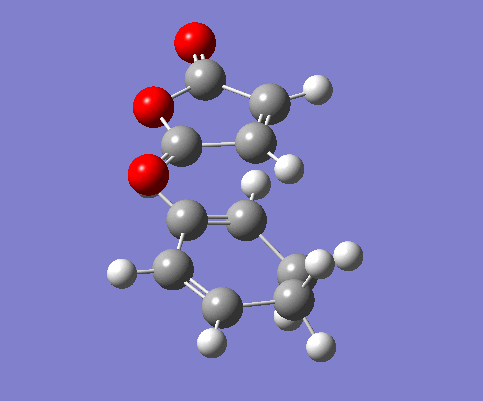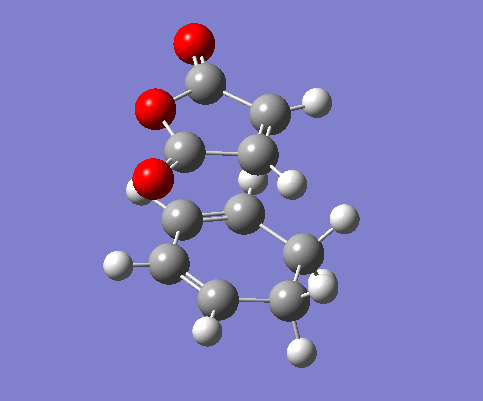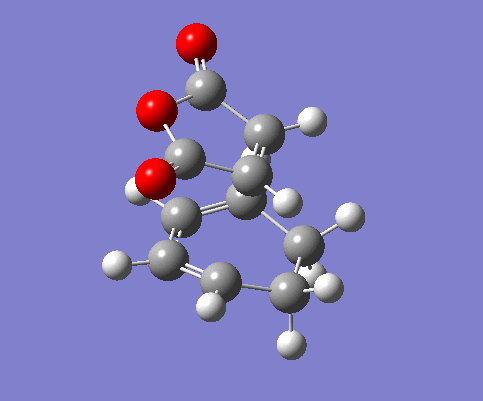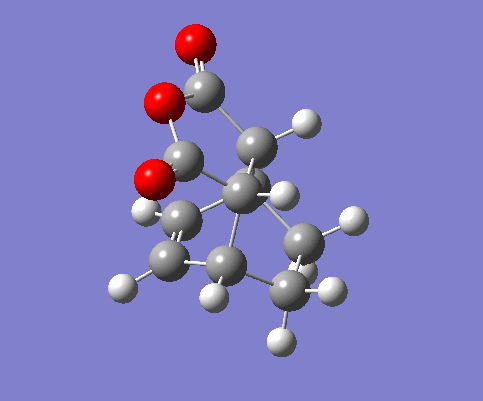
Endo Structure	Exo Structure

Important Results

TS	Endo	Exo
Energy (Ha)	-612.6833957	-612.6793354
Partially formed C-C bond distance (Å)	2.27	2.29
Carbonyl carbon of dienophile and the nearest carbon on the diene distance (Å)	2.99	3.03

Summary Table

Transition State	Endo	Exo
File Name	TC_DA_2_endo_optfreq_b3lyp_631g_d_keywords	TC_DA_2_exo_optfreq_b3lyp_631g_d_keywords
File Type	.log	.log
Calculation Type	FREQ	FREQ
Calculation Method	RB3LYP	RB3LYP
Basis Set	6-31G(d)	6-31G(d)
Charge	0	0
Spin	Singlet	Singlet
Energy	-612.68339577 a.u.	-612.67933543 a.u.
RMS Gradient Norm	0.00000093 a.u.	0.00000028 a.u.
Imaginary Freq	1 (-447 cm-1)	1 (-448 cm-1)
Dipole Moment	6.1143 D	5.5504 D
Point Group	C1	C1
Computational Time	1 hr 7 min 15.7 sec	57 min 34.5 sec
Log File	[Endo TS (DFT opt)]	[Exo TS (DFT opt)]
Item Table	Item Value Threshold Converged? Maximum Force 0.000001 0.000015 YES RMS Force 0.000000 0.000010 YES Maximum Displacement 0.000035 0.000060 YES RMS Displacement 0.000008 0.000040 YES Predicted change in Energy=-1.291769D-11 Optimization completed. -- Stationary point found..	Item Value Threshold Converged? Maximum Force 0.000001 0.000015 YES RMS Force 0.000000 0.000010 YES Maximum Displacement 0.000045 0.000060 YES RMS Displacement 0.000009 0.000040 YES Predicted change in Energy=-8.710799D-11 Optimization completed. -- Stationary point found..

The relative energies of the endo and exo transition states are -612.6833957 a.u. and -612.6793354 a.u. respectively. As the reaction is kinetically controlled, it can be deduced that the reaction would prefer to proceed via the endo transition state due to it being lower in energy compared to its counterpart, the exo transition state. In addition, although the structures are similar, the distances between the reactants are different. For instance, the partially formed C-C bond was calculated to be 2.27 Å and 2.29 Å for the endo and exo form, respectively. The separation can be seen in greater effect when comparing the distance between the carbonyl carbons of the dienophile and the nearest carbon on the diene, which was determined to be 2.99 Å for the endo form and 3.03 Å for the exo form. This is indication that the exo transition state suffers from steric strain due to the bulkier sections of both reactants pointing in the same direction. Moreover, in the exo transition state, the -(C=O)-O-(C=O)- fragment of maleic anhydride points in the direction of the two -CH₂ groups in cyclohexa-1,3-diene, whereas tin the endo form, the -(C=O)-O-(C=O)- fragment points towards the diene end with the -CH groups. The extra hydrogen on the carbon causes extra sterics and therefore lack of space, leading to a more strained structure for the exo form. This is likely to be one of the reasons for the preference for the reaction to proceed via the endo transition state.

The MOs, in particular the HOMO and LUMO, of the two different transition states were again examined in order to investigate further into possible orbital interactions in the reaction. The visualisations can be seen below.

endo HOMO MO	exo HOMO MO

In the case of the Diels Alder reaction between maleic anhydride and cyclohea-1,3-diene, the electron withdrawing nature of the dienophile causes the lowering of energy levels of its HOMO and LUMO. This causes the HOMO of the transition state to be selectively asymmetric (as) in nature, as the energy difference between the asymmetric and symmetric pairing is majorly different (i.e. ΔE_AS < ΔE_S) and the reaction would favour the pairing of the orbitals of similar energy.

The HOMO and LUMO of maleic anhydride and cyclohexa-1,3-diene

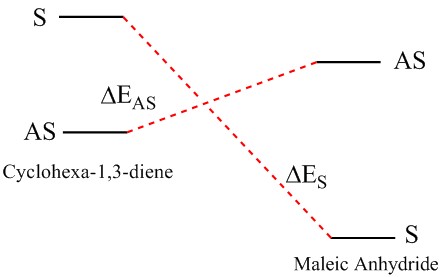
On top of the steric and strain effects, examination of the orbitals involved highlights another explanation for the preference for the endo transition state for the reaction, and that is the 'Secondary Orbital Effects', as first proposed by Woodward and Hoffman . The origin of the effect comes from the oxygen of in the maleic anhysride offering π orbital interaction, resulting in the stabilisation of the transition structure and lowering of activation energy.

The Secondary Orbital Effect requires alignment of the available π orbitals, in this case the π orbitals of the oxygens in the malelic anhydride, with the diene fragment involved in the Diels Alder cycloaddition. This is only available for the endo transition state, as the oxygen components are properly aligned above the diene of the cyclohexadiene. In the exo form, the -(C=O)-O-(C=O)- fragment are orientated in the opposite direction to the diene involved in the reaction and therefore does not experience the stabilising effect.

The frequency analysis of the exo and endo form were also ran during the optimisation. The imaginary frequency (animated below) describes this transition state.

Imaginary Frequency

Endo	Exo
Frequency = -447 cm-1	Frequency = -448 cm-1

The concerted motion corresponds to the Diels Alder reaction. In addition, the animations suggests synchronous formation of the new C-C bonds.

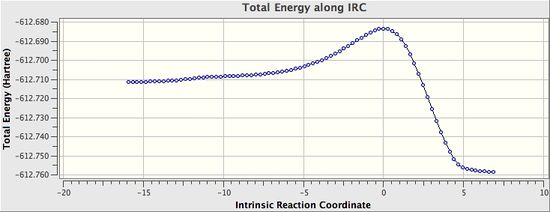
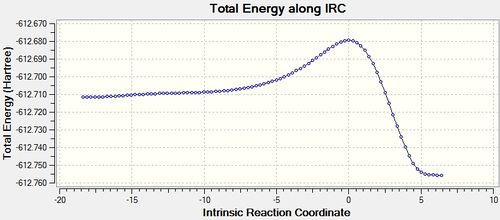
The IRC was also calculated in order to both ascertain the transition state as well as obtain more information about the reaction. The outcome can be seen below.

Endo IRC

Exo IRC

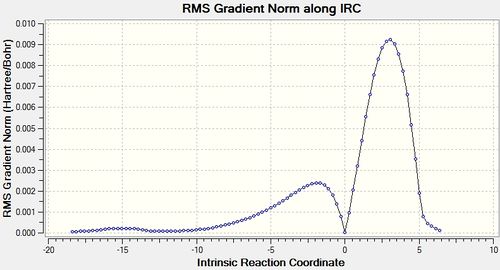
From the IRC results, it can be seen that, the transition states obtained both reasonably connect the reactants and the product. Although the final structures from the IRC are not the perfectly optimised structure with minimised energy (from the RSM gradient norm values), it is sensible to conclude that they are fairly close to the final optimised structure, thereby suggesting the reactions, with the located transition states, are feasible.

Solvation Effects

The solvation effects was also studied using gaussian. This was performed using the solvation tab by selecting the default under models and selecting the appropriate solvent to be studied. The chosen solvents, based on differences in the dielectric constant, were heptane, methanol and water. It is worth mentioning that the solventation mechanism in gaussian 'paints' a background of dielectric charge around the molecule being studied, the cavitation is changed based on the chosen model. It is expected that the polar solvents would stabilise the transition state for both the exo and endo. The optimisation of the endo and exo transition states were performed separately in the default solvation model with water, methanol and heptane. The energies of the different optimisations with different solvents, along with the previous optimisation with no solvation (treated as reaction in the gas phase), were compared in order to investigate the effect in which the solvent has on the transition state. The results are plotted in the graph below along with the table of results.

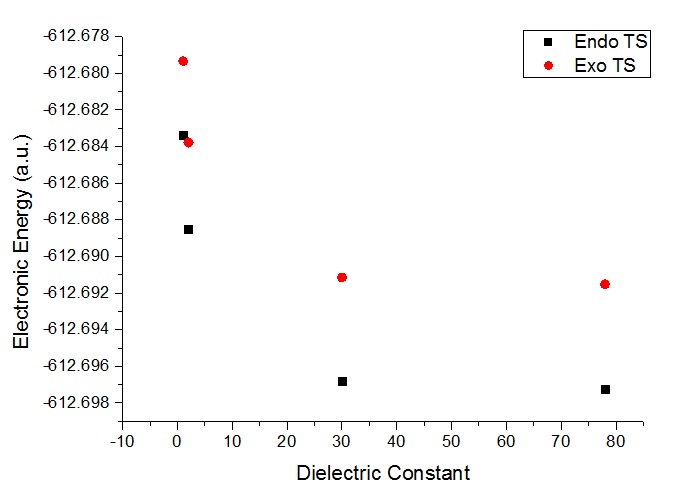
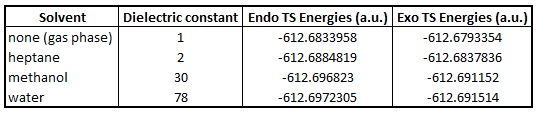
As expected, the more polar the solvent, the more stabilised the transition states become. The effect is observed for both the endo and exo forms. This is likely due to the fact that the background of dielectric charge help to stabilise the charge of the transition states, i.e. the charge is spreads out over more atoms. However, it can be seen that the solvent stabilisation effect plateaus as the dielectric constant increases and that the shape of the curve follows a exponential decay. This suggests that the 'spreading' of the charge reaches a maximum value as the dielectric constant increases.

Conclusion and Further Discussion

The computational study of the transition states above for the Cope rearrangement and the Diels Alder cycloaddition has resulted in some interesting findings. For example, it was observed that the Cope rearrangement of the 1,5-hexadiene preferred to go proceed via the Chair transition state. The Diels Alder reaction between maleic anhydride and cyclohexa-1,5-diene favours the endo transition state rather than the exo due to both the steric and strain interactions as well as the important secondary orbital interactions.

For the Diels Alder reaction between maleic anhydride and cyclohexa-1,3-diene, although satisfactory results have been obtained, there are a few factors which have been neglected. The investigation of solvent effects had suggested that stabilisation occurs as you increase the polarity of the solvent. A fuller picture can be obtained if more solvent was investigated. In addition, although the built in solvation capability in gaussian alters the dielectric constant of the environment the optimsiation is performed in, it does not model specific interactions, such as hydrogen bonding. In order to investigate the point interactions, extra molecules such as water molecules have to be drawn and optimisated. Investigation into important specific interactions could offer addition useful information into the reactivity of the reaction. Although, not a neglected effect, but the comparison of the relative magnitudes of the steric effects and the secondary orbital effects could improve the investigation into the Diels Alder cycloaddition.

Furthermore, the gaussian calculation for the transition state only considers the minimum energy path and it considers only a single molecule of reactants going into one single transition state, whereas in reality, the molecules would collide and proceed via many different routes. This has a consequence on the energy values which are produced in the results. The collisions of many molecules and reaction paths of higher energy are not calculated and these could be investigated in order to understand more about the reaction.

In addition, the Diels Alder reaction is a movement of six electrons in a concerted motion. Therefore, one might expect the transition state of the cycloaddition to be aromatic. The aromaticity of the transition state can be investigated using the NICS (nucleus independent chemical shift) method. The method is performed by placing a ghost atom in the middle of an aromatic structure and computationally calculating the NMR in order to examine the shielding that may arise in the ghost atom. The negative value of the result is taken, therefore, if the result is negative than the structure can be said to be aromatic. The result would offer additional information on the electrons involved in the reaction, the arrangement of the system as well as the stability of the transition state. These are all factors that have thus been neglected in the calculations of Diels Alder transition state.

Nevertheless, in all computational studies, it is important to understand the limitations and the theory as well as the assumption that are used in these calculations. For instance, the B3LYP/6-31G* are better suited for investigating energies, whereas the AM1 Semi-empirical or Hartree Fock method is preferred for examining molecular orbitals.