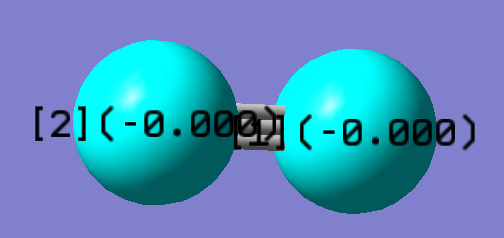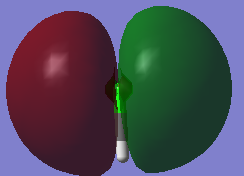Rep:Mod:HEL1987
NH3
test molecule |
About the molecule
Name of molecule : Ammonia
Calculation Method : RB3LYP
Basis Set : 6-31G(d,p)
E(RB3LYP) : -56.55776873a.u.
RMS Gradient Norm : 0.00000485a.u.
Point Group : C3V
Geometric Information of Meolecule
N-H bond length : 1.01798 Å
H-N-H bond angle (optimised) : 37.129°
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000070 0.001800 YES
RMS Displacement 0.000033 0.001200 YES
Predicted change in Energy=-5.785199D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
For more information on the optimised molecule, go to here
The following contains information on vibration frequencies and their IR values.
Questions
Answering questions on vibrational modes of ammonia: 1) From the 3N-6 rule, 6 number of modes are expected to be seen. 2) Modes 5 and 6 are degenerate. Both have the same frequency of 3589.82 Hz which means they also have the same energy. Modes 2 and 3 are also degenerate. Both have the same frequency of 1693.95 Hz which means they also have the same energy. 3) Modes 1,2 and 3 are "bond stretch" vibrations. Modes 4,5, and 6 are "bending" vibrations. 4) Mode 4 is highly symmetric. 5) Mode 1 is known as "umbrella" mode. 6) 2 bands are expected to be seen in an experimental spectrum of gaseous ammonia. These bands are from modes 1 and 2 and 3. Mode 2 and 3 share the exact same frequency and will appear in the same band. Intensity of mode 5 and 6 are too low to be observed. In addition, mode 5 and 6 only cause very minimal change in dipole so it remains IR inactive. Mode 4 does not cause a change in dipole so it is infrared inactive.
Charges on atoms
The expected charge for the N atom is negative.
The expected charge for each of the H atoms are positive.
This expectation is based on the fact that N is much more electronegative than H.
Electronegativity of N is 3.041. Electronegativity of H is 2.21.
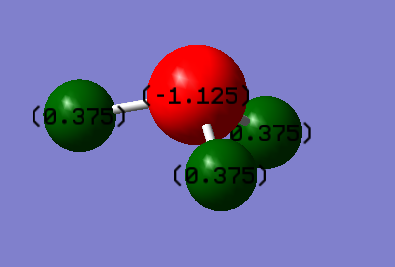
The following is the calculated charges using Schrodinger equation on Gaussview:
The charge on the N atom is -1.1.125.
The charge on each of the H atoms is 0.375.
N2
test molecule |
About the molecule
Name of molecule : Nitrogen
Calculation Method : RB3LYP
Basis Set : 6-31G(d,p)
E(RB3LYP) : -109.52412868a.u.
RMS Gradient Norm : 0.00000060a.u.
Point Group : Dinfh
Geometric Information of Molecule
N-N bond length : 1.10550 Å
N-N bond angle : 180°
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.383672D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
For more information on the optimised molecule, go to here
The following contains information on vibration frequency and its IR value.
Summary of the vibrational mode of nitrogen molecule: 1) Diatomic molecules such as nitrogen only has one normal mode of vibration. 2) No bands will appear in the experimental spectrum of nitrogen. This is due to the fact that its "bond stretch" vibrations do not cause a change in dipole so it remains IR inactive.
Charges on atoms
Each of the N atom is not expected to be charged. Their electronegativities are exactly the same (3.04). So their difference in electronegativity is 0.
The following is the calculated charges using Schrodinger equation on Gaussview:
H2
test molecule |
About the molecule
Name of molecule : Hydrogen
Calculation Method : RB3LYP
Basis Set : 6-31G(d,p)
E(RB3LYP) : -1.17853936a.u.
RMS Gradient Norm : 0.00000017a.u.
Point Group : Dinfh
Geometric Information of Molecule
H-H bond length : 0.74279 Å
H-H bond angle : 180°
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
For more information on the optimised molecule, go to here
The following contains information on vibration frequency and its IR value.
Summary of the vibrational mode of hydrogen molecule: 1) Diatomic molecules such as hydrogen only has one normal mode of vibration. 2) No bands will appear in the experimental spectrum of hydrogen molecule. This is due to the fact that its "bond stretch" vibrations do not cause a change in dipole so it remains IR inactive.
Charges on atoms
Each of the H atom is not expected to be charged. Their electronegativities are exactly the same (2.2). So their difference in electronegativity is 0.
Haber-Bosch calculation
Reaction energy calculation of Haber process: 1) E(NH3) = -56.55776873 a.u 2) 2*E(NH3) = -113.1155375 3) E(N2) = -109.52412868 a.u 4) E(H2) = -1.17853936 a.u 5) 3*E(H2) = -3.53561808 a.u 6) ΔE =2*E(NH3)-[E(N2)+3*E(H2)] = -0.05579074 a. u = -146.48 kJ/mol
HCl
test molecule |
About the molecule
Name of molecule : Hydrogen Chloride
Calculation Method : RB3LYP
Basis Set : 6-31G(d,p)
E(RB3LYP) : -460.80077875 a.u.
RMS Gradient Norm :0.00005211 a.u.
Point Group :Cinfv
Geometric Information
H-Cl bond length : 1.28599 Å H-Cl bond angle : 180°
Item Value Threshold Converged?
Maximum Force 0.000090 0.000450 YES
RMS Force 0.000090 0.000300 YES
Maximum Displacement 0.000139 0.001800 YES
RMS Displacement 0.000197 0.001200 YES
Predicted change in Energy=-1.256951D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.286 -DE/DX = 0.0001 !
--------------------------------------------------------------------------------
For more information on the optimised molecule, go to here
The following contains information on vibration frequency and its IR value.
Summary of the vibrational mode of HCl molecule: There is only one vibrational mode because HCl is a linear molecule. The H atom vibrates much more than the Cl atom because it is lighter and smaller in size. The mode causes a change in dipole making HCl IR active.
Expected charges on atoms
1) Cl is expected to have a negative charge.
2) H is expected to have a positive charge.
3) This is because Cl is much more electronegative than H.
4) Electronegativity of Cl = 3.161. Electronegativity of H = 2.201</>.
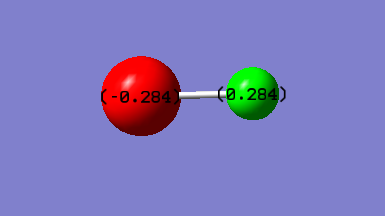
The following is the calculated charges using Schrodinger equation on Gaussview:
MOs of HCl
The MO of non-bonding 3s orbital of Cl. This molecular orbital is very deep in energy and is not involved in bonding. This MO is occupied by 2 electrons from the 3s orbital of Cl. The shape of this MO is distorted. This might be because its energy of -0.84773 is quite close to the bonding MO energy of -0.47433.
The MO of a bonding orbital σ3pz. This orbital is occupied by one electron from the 3pz atomic orbital of HCl and one elctron from the 1s atomic orbital of H.
The MO orbital of 3px atomic orbital of Cl. This is a non-bonding orbital and it is also the HOMO. It is occupied by two electrons from the 3px atomic orbital of Cl.
The MO orbital of 3py atomic orbital of Cl. This is a non-bonding orbital and it is also the HOMO. It is occupied by two electrons from the 3py atomic orbital of Cl. This MO is degenerate with the 3px MO.
The MO orbital of 3pz atomic orbital of Cl. This is an anti-bonding orbital and it is also the LUMO.
Cl2
test molecule |
About the molecule
Name of molecule : Chlorine
Calculation Method : RB3LYP
Basis Set : 6-31G(d,p)
E(RB3LYP) : -920.34987886 a.u
RMS Gradient Norm : 0.00002510 a.u
Point Group : Dinfh
Calculation of reaction energy of HCl
Reaction energy of formation of HCl: 1) E(H2) = -1.17853936 a.u 2) E(Cl2) = -920.34987886 a.u 3) E(HCl) = -460.80077875 a.u 4) 2*E(HCl) = -921.6015575 a.u 5) ΔE =2*E(HCl)-[E(H2)+E(Cl2)] = -1840.772897 a.u = -4832949.24 kJ/mol
References
1. https://www.angelo.edu/faculty/kboudrea/periodic/trends_electronegativity.htm