Rep:Mod:HD1311

The Cope Rearrangement of 1,5-hexadiene

The Cope Rearrangement of 1,5-hexadiene is a [3,3]-sigmatropic reaction, the reaction mechanism has been the subject of many researches. It is commonly agreed that the reaction proceeds via either chair or boat transition state in a concerted synchronous fashion with boat transition state slightly disfavored. The aims of this exercise is to locate low-energy minima and transition structures on the potential energy surface of 1,5-hexadiene so that the preferred reaction mechanism can be determined.

Scheme 1. Reaction scheme of Cope-rearrangement of 1,5-hexadiene

Optimizing the Reactants and Products

Four conformers of 1,5-hexadiene are shown in Table 1. along with their energies and point groups. (from left to right in turn (a), (b) (c), (d)).

A conformer (a) of 1,5-hexadiene with an "anti" linkage for the central four carbon atoms was optimized at the HF/3-21G level of theory. The energy and point group associated with this structure are -231.69097 Ha and C1 respectively. The energy of another conformer (b) of the same molecule with a "gauche" linkage for the central four carbon atoms optimized at the same level of theory was calculated to be -231.69167 Ha. By comparing the energies of (a) and (b), one can postulate that the lowest energy conformer lies within gauche conformations. Thereby, gauche conformer (c) of 1,5-hexadiene with lowest energy postulation was drawn and tested. Indeed, by comparing final results with Appendix 1, (c) corresponds to gauche 3, which is the lowest energy conformation. (a) and (b) correspond to anti4 and gauche2 respectively. However, this does not agree with conventional rules of organic chemistry which indicates that anti conformation is lowest in energy. This is due to the basis set 3-21G used here is relatively simple and it does not include electronic correction. Literature calculation with larger basis set which includes electronic correction agrees with the conventional chemistry.

(a)anti4	(b) gauche2	(c) gauche3	(d) anti2
HDanti4final.mol	react_gaucheb.mol	REACT-C true lowest.mol	REACT_F_HF.mol
-231.69097 Ha (C1)	-231.69167 Ha (C2)	-231.69266 Ha (C1)	-231.69254 Ha (Ci)

Table 1. Four conformers of 1,5-hexadiene

Anti2 conformation with C_i symmetry was optimized at the HF/3-21G level of theory ((d) in Table 1), followed by re-optimization at the B3LYP/6-31G* level of theory. 6-31G* adds polarisation functions to atoms therefore it produces better description of orbitals than 3-21G does. Table 2 illustrates key differences in terms of geometry before and after re-optimization.

Before re-optimization	After re-optimization
REACT_F_HF_anti2.mol	HD1311anti2B3LYP.mol
anti2 optimized at HF/3-21G	anti2 re-optimized at B3LYP/6-31G*

Table 2. Optimization of anti2 conformer at HF/3-21G and B3LYP/6-31G*(File:REACT F HF.LOG)

After re-optimization, the energy of anti2 conformer shows to be -234.61170 Ha. The dihedral angle (180^o) and point group (C_i) remain constant. However, bond angles have increased by an average of about 1^o. Therefore, one can conclude that geometry change associated with the re-optimization at the B3LYP/6-31G* level of theory is negligible.

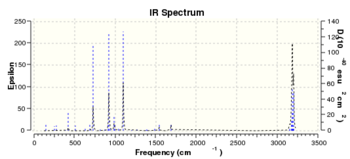
Following re-optimization of anti2 conformer, a frequency calculation was performed and the results are illustrated in Table 3, in which different types of energies are demonstrated: i) the sum of electronic and zero-point energies (potential energy at 0K and zero-point vibrational energy) ii) the sum of electronic and thermal energies (energy at 298.15K and 1 atmospheric pressure including translational, rotational and vibrational modes) iii) the sum of electronic and thermal enthalpies (including correction for RT) iv) the sum of electronic and thermal free energies (including entropic contribution to the free energy). A simulated Infra-red spectrum was generated based upon the frequency calculation is shown in Figure 1.

Types of energies	Notation	Energy Hartree
Sum of electronic and zero-point energies	E = Eelec + ZPE	-234.46921
Sum of electronic and thermal energies	E = E + Evib + Erot + Etrans	-234.46186
Sum of electronic and thermal enthalpies	H = E + RT	-234.46091
Sum of electronic and thermal free energies	G = H - TS	-234.50082

Table 3. Frequency calculation of anti2 conformer (B3LYP/6-31G*)(File:REACT G B3LYP FREQUENCY.LOG)

Figure 1. Simulated IR spectrum of anti2 conformer (B3LYP/6-31G*)

Types of energies	anti4	gauche2	gauche3
Sum of electronic and zero-point energies	-231.53785	-231.53871	-231.53949
Sum of electronic and thermal energies	-231.53096	-231.53179	-231.53265
Sum of electronic and thermal enthalpies	-231.53002	-231.53085	-231.53170
Sum of electronic and thermal free energies	-231.56891	-231.56948	-231.57064

Table 4. Frequency calculations of conformer (a), (b) and (c) at HF/3-21G

(File:ANTI4FREQUENCY.LOG;File:GAUCHE2FREQUENCY.LOG;File:GAUCHE3FREQUENCY.LOG)

Optimizing the "Chair" and "Boat" Transition Structures

The transition state of the Cope rearrangement was studied using various computational approaches in Gaussian.

Figure 2. Chair and boat transition structure of the Cope Rearrangement

Chair transition state

In this section, chair transition structures was investigated using two different methods: 1. by computing force constant matrix (known as Hessian) into optimization. 2. the use of frozen reaction coordinate method: the reaction coordinate is frozen at first and the rest of the transition structure is optimized to a minimum. Once the structure is completely relaxed, the coordinate can be unfrozen and the transition structure is optimized again.

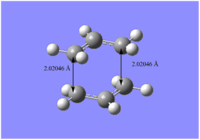
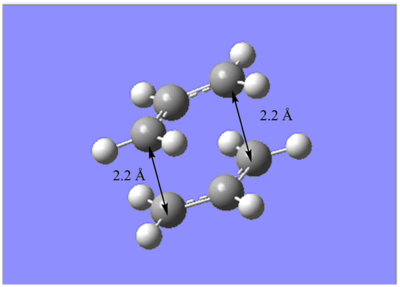
An allyl fragment (CH₂CHCH₂) was drawn and optimized at the HF/3-21G level of theory. This optimized fragment was then used to generate a guessed chair transition structure via duplication and rotation. (Figure 3). The distance between the terminal ends of the allyl fragments is about 2.2 Å.

Figure 3. Guessed chair transition structure composed of two allyl fragments

The guessed chair transition structure was then optimized with frequency calculation at the HF/3-21G level of theory incorporating method 1, in which the force constant was set to calculate once and optimization to a TS (Berny). The results show an imaginary frequency at -818 cm^-1 with animation confirmed corresponding to Cope rearrangement Figure 4. The electronic energy and point group associated with this transition structure were calculated to be -231.619322 Ha and C_2h respectively.

Figure 4. Animation of Cope Rearrangement via chair transition state

Previously, the guessed transition structure was optimized using method 1 at the HF/3-21G level of theory. In order to study the difference in outcome between using different methods. the guessed transition structure was optimized again using method 2 at the same level of theory.

'	Method 1 outcome	Method 2 outcome
Electronic energy/Ha	-231.61932	-231.61932
Picture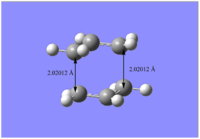
	File:HDCHAIR TS B.LOG	File:HDCHAIR TS D.LOG

Table 5. Comparison of results for the guessed chair transition structure optimized using method 1 and 2 at the HF/3-21G level of theory

From Table 5, one can see that the differences in terms of geometry and energy are trivial and both methods worked well. This is due to good matching between guessed transition structure and the actual transition structure. However, in the case of larger and more complicated molecule where proposed transition structure is far from the exact structure, method 2 (frozen reaction coordinate) is more favored.

Following optimization of the guessed transition structure at the HF/3-21G level of theory. It was re-optimized at the B3LYP/6-31G* level of theory. Due to the consistency in results between using method 1 and 2, either of the results can be used to continue with the re-optimization. In this case, method 1 result was chosen. There is insignificant change in geometry but considerable differences in energies before and after re-optimization as summarized in Table 6.

Energy Type	Energy/Hartree (HF/3-21G)	Energy/Hartree (B3LYP/6-31G*)
Electronic energy	-231.61932	-234.55698
Sum of electronic and zero-point energies	-231.46670	-234.41493
Sum of electronic and thermal energies	-231.46134	-234.40901
Sum of electronic and thermal enthalpies	-231.46040	-234.40807
Sum of electronic and thermal free energies	-231.49520	-234.44381
Imaginary Frequency / cm-1	-818	-566
Simulated IR spectrum

Table 6. Frequency calculations of chair transition structure at HF/3-21G and B3LYP/6-31G* (File:HDCHAIR TS B3LYP(G).LOG)

Boat transition state

The boat transition state was optimized using QST2 method. In this method, the transition structure is determined via interpolation between the specified reactant and product of a reaction.

An input file with i and ii structures (Table 7) was generated (the numbering of the product molecule was changed with respect to the reactant molecule so that it corresponds to the numbering obtained if the reactant had rearranged) followed by optimization with frequency calculation at HF/3-21G level of theory incorporating QST2 method in order to locate the boat transition structure. The optimization failed and gave a twisted structure because the reactant and product were not close in terms of geometry to the boat transition structure. Therefore, reactant and product were modified to give iii and iv structures. The same calculation was run again and this time, the boat transition structure was successfully located. The electronic energy of this transition state is -231.60280 Ha with C_2v point of symmetry. The frequency calculation showed an imaginary frequency with magnitude of 840 cm^-1.(Figure 5)

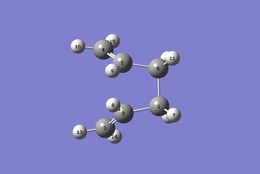
i (reactant)	ii (product)	iii (reactant)	iv (product)

Table 7. Geometries of reactant and product before modification (i, ii) and after modification (iii, iv)

Figure 5. Animation of Cope Rearrangement via boat transition state

The optimized boat transition structure was re-optimized at B3LYP/6-31G* level of theory. (Table 8)

Energy Type	Energy/Hartree (HF/3-21G)	Energy/Hartree (B3LYP/6-31G*)
Electronic energy	-231.60280	-234.54309
Sum of electronic and zero-point energies	-231.45093	-234.40234
Sum of electronic and thermal energies	-231.44530	-234.39601
Sum of electronic and thermal enthalpies	-231.44436	-234.39506
Sum of electronic and thermal free energies	-231.47977	-234.43175
Imaginary Frequency / cm-1	-840	-530
Simulated IR spectrum

Table 8. Frequency calculations of boat transition structure at HF/3-21G and B3LYP/6-31G*(File:HDTS E MODIFIED.LOG; File:HDTS E MODIFIED(BOAT)B3LYP(G).LOG)

Intrinsic Reaction Coordinate (IRC)

Intrinsic reaction coordinate allows us to locate the structure of product by following the transition structure down to its local minimum on a potential energy surface.

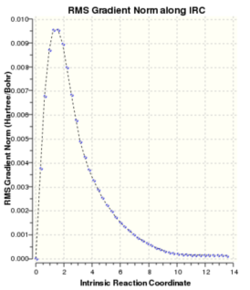
Hessian optimized chair transition structure was chosen to do the IRC analysis. The results are illustrated in Table 9(50 points on IRC)

HDchairtransititionstructure
S1	G1	G2

Table 9. IRC analysis of Hessian optimized chair transition structure File:HDCHAIR TS F.LOG

S1 corresponds to the last point generated along IRC with electronic energy -231.69158 Ha. By comparing the structure and its corresponding energy with Appendix 1. It does not match any of the structures listed in the table. Therefore, one can conclude the minimum energy geometry has not been reached. There are three approaches can be considered in order to reach the lowest energy geometry. First method: Taking the last point and run a minimization. Second method: Restart the IRC with larger number of points until the minimum structure is located. Third method: Redo the IRC with force constants computed at every step. Third method is the most reliable but may not be possible for large systems.

For the case here, method one was picked up because S1 is very close to the local minimum and the analyzing result (Figure 6)corresponds to gauche2 conformer.

HF_FCHairmehod1.mol2

Figure 6. IRC Re-calculation using method one

Activation Energy

The activation energies of Cope Rearrangement were calculated via both chair and boat transition structures. (Table 10)

'	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)/ (kcal/mol)	45.71	44.70	34.06	33.16	33.5 ± 0.5
ΔE (boat)/ (kal/mol)	55.60	54.76	41.96	41.32	44.7 ± 2.0

Table 10. Calculation of activation energies of Cope rearrangement via both chair and boat transition structures (File:HDTS E MODIFIED(BOAT)B3LYP(G)(0K).LOG; File:HDTS E MODIFIED(0K).LOG; File:HDCHAIR TS B3LYP(G)(0K).LOG; File:HDCHAIR TS B(0K).LOG)

The activation energies were calculated by measuring the difference in energy between reactant (anti2) and transition structures. By comparing the activation energies for two transition states, one can see that overall chair transition state has lower activation energy thus it is more favored. For both transition structures, B3LYP/6-31G* gives better estimation of transition states because the activation energies calculated at 0 K are closer to experimental values at B3LYP/6-31G* level of theory than HF/3-21G.

The Diels Alder Cycloaddition

Cis-butadiene

Cis-butadiene was optimized using AM1 semi-empirical molecular orbital method. The corresponding HOMO (Figure 7) and LUMO (Figure 8) after optimization were plotted with HUMO being anti-symmetric and LUMO being symmetric with respect to the plane. (File:I)CISBUTADIENEOPTIMIZATION.LOG)

Figure 7. HOMO of Cis-butadiene

Figure 8. LUMO of Cis-butadiene

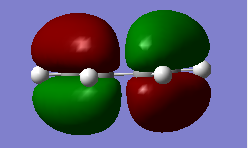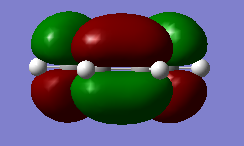Study of transition state of cycloaddition between ethylene and cis-butadiene

The guessed transition structure (a) was obtained by drawing molecule (b) followed by removing the -CH₂-CH₂ fragment. (Figure 9). The interfragment distance (dashed lines) were set to be about 2.2 Å.

Figure 9. Guessed transition structure for cycloaddition of ethylene and cis -butadiene

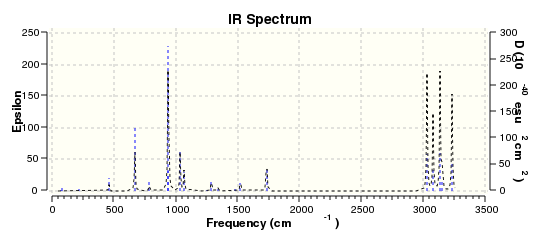
(a) was then optimized with frequency calculation using Hessian method at AM1 semi-empirical level of theory. The interfragment distance (dashed lines) were set to be about 2.2 Å. The resulting optimized transition structure has one imaginary frequency with magnitude of 956 cm^-1. The corresponding animation is shown in Figure 10, from which one can see that two fragments approaching and leaving each other synchronously, indicating concerted bond formation. The simulated IR spectrum is given in Figure 11. The lowest positive vibration frequency is 147 cm^-1 and it corresponds to the vibration of reactant molecules.

Figure 10. Animation of cycloaddition between ethylene and cis-butadiene File:II)TRANSITIONSTATE.LOG

Figure 11. Simulated IR spectrum of transition state of reaction between ethylene and cis-butadiene

After optimization, the bond lengths of partly formed σ C-C bonds are 2.12 Å. Typical sp3 and sp2 C-C bond lengths are 1.54 Å and 1.47 Å respectively and the van der Waals radius of C atom is 1.70 Å. Although the partly formed σ C-C bonds are longer than the typical bond lengths, they are still within the van der Waals radius, indicating bond forming interactions between the C atoms.

Figure 12. HOMO (anti-symmetric) of transition state

Figure 13. LUMO (symmetric) of transition state

The HOMO (Figure 12) of the transition structure is a (anti-symmetric),since orbitals can only overlap with correct symmetry, this MO is formed using the HOMO of cis-butadiene (a) and the LUMO of ethylene (a).

Cyclohexa-1,3-diene reaction with maleic anhydride

The guessed endo- and exo- transition structures for the reaction between cyclohexa-1,3-diene and maleic anhydride were drawn Figure 14. These two transition structures were then optimized with frequency calculation using Hessian method at AM1 semi-empirical level of theory with interfragment distances (dashed lines) set to be approx 2.2 Å.

Figure 14. Guessed endo- and exo- transition structures for reaction between cyclohexa-1,3-diene and maleic anhydride

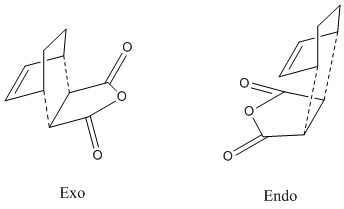
After optimization, the transition structures were successfully located with results summarized in Table 11.

'	Endo-transition state	Exo-transition state
Electronic energy / Ha	-0.05150	-0.05042
Sum of electronic and zero-point energies / Ha	0.13350	0.13488
Sum of electronic and thermal energies / Ha	0.14368	0.14488
Sum of electronic and thermal enthalpies / Ha	0.14463	0.14583
Sum of electronic and thermal free energies / Ha	0.09735	0.09912
Animation	Figure 15.	Figure 16.
Imaginary frequency / cm-1	-806	-812
HOMO	Figure 17.	Figure 18.
Bond length	Figure 19.	Figure 20.
Secondary orbital overlap effect	Figure 21.	Figure 22.
	File:ENDOTS.LOG	File:EXOTS.LOG

Table 11. Summary of properties of optimized exo- and endo- transition state

The electronic energy of endo-transition structure ( -0.05150 Ha) is lower than that of exo-transition state (-0.05042 Ha), since the reaction is supposed to be kinetically controlled, the endo-transition state is more favored. In addition, secondary orbital overlap effect introduces stabilization to the endo-transition state by possible overlap interactions between p orbitals of carbonyl groups and p orbitals of ethylene group.

Both transition structures have one imaginary frequency with magnitude of 806 cm^-1 (endo) and 812 cm^-1 (exo). The corresponding animations are shown in Figure 15 and Figure 16.

The partly formed σ C-C bond lengths are 2.16 Å (endo) and 2.17 А (exo). Other C-C through space distances are shown in Figure 19 and Figure 20: For endo-transition state: C₁-C₁₅ and C₄-C₁₈ are 2.89 Å; For exo-transition state: C₁₂-C₁₈ and C₉-C₁₅ are 2.95 Å. Exo-transition state generally has longer through space bond distance than endo due to greater steric repulsion, which is generated by extra H attached to the sp³ hybridized carbon (C₁₂, C₉, Figure 20) than sp² hybridized carbon (C₁, C₄ Figure 19).

Further Work

'	Endo	Exo
Transition state	ENDOTSREOP6-31G.mol	EXOTSREOPT6-31G.mol
Partly formed C-C bond length / Å	2.27	2.29
Electronic Energy / Ha	-612.68340	-612.67931
Log file	File:ENDOTSREOP6-31G.LOG	File:EXOTSREOPT6-31G.LOG‎

Table 12. Summary of properties of re-optimized exo- and endo- transition state at B3LYP/6-31G* level of theory

The AM1 semi-empirical method optimized transition structures were re-optimized at B3LYP/6-31G* level of theory according to and modified from published work written by Kamyar Afarinkia. The results are summarized in Table 12, the reason to do this re-optimization is because when using the AM1 semi-empirical method, all two electron integrals involving two-center charge distributions are neglected.

From results in Table 12, one can see that the electronic energies of the re-optimized transition structures are significantly lower than that optimized at AM1/semi-empirical level of theory. The partly formed σ C-C bonds are slightly longer as well.