Rep:Mod:HChauhan2616
Ammonia (NH3)
Summary
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy E(RB3LYP) | -56.55776873 a.u. |
| Point Group | C3V |
| RMS Gradient | 0.00000485 a.u. |
| NH Bond Length | 1.01798 Å |
| H-N-H Bond Angle | 105.741o |
| Item | Value | Threshold | Converged? | |
|---|---|---|---|---|
| Maximum | Force | 0.000004 | 0.000450 | YES |
| RMS | Force | 0.000004 | 0.000300 | YES |
| Maximum | Displacement | 0.000072 | 0.001800 | YES |
| RMS | Displacement | 0.000035 | 0.001200 | YES |
.LOG File: Media:HC2616_NH3_OPTF_POP.LOG
Ammonia |
Vibrational Data
Questions
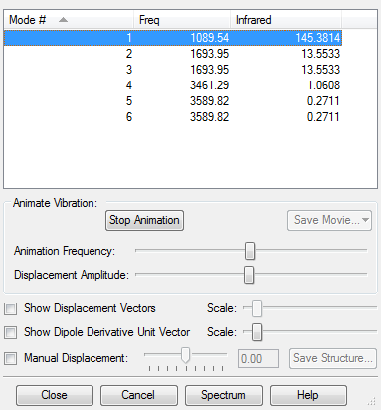
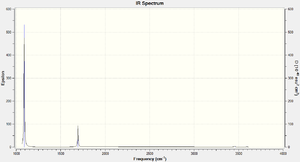
Using the 3N-6 vibrational modes rule, where N = 4, 6 vibrational modes are expected. Modes 2 and 3 are degenerate as well as 5 and 6. Modes 1, 2 and 3 are bending modes and 4,5 and 6 are streching modes. Mode 4 is a highly symmetric bending mode. Mode 1 is known as the "umbrella" mode. 4 bands would be expected to be seen in an experimental spectrum of ammonia gas due to 2 sets of 2 degenerate vibrational modes. The predicted IR spectrum from Gaussview is shown below.
2 bands can be clearly distinguished 1090 and 1694 cm-1 and two bands, with much lower intensities at 3461 and 3590 cm-1
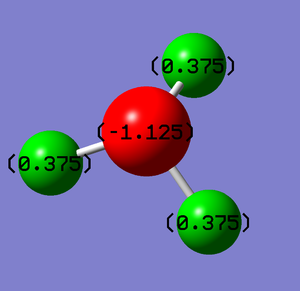
Charge Data
The nitrogen atom has a charge of -1.125 and each hydrogen atom has a charge of 0.375. This is expected as nitrogen has a higher electronegativity than hydrogen, thus it draws electron density away from the hydrogen atoms, giving it an overall negative charge. The hydrogen atoms have a positive charge to make the molecule neutral overall.
Nitrogen (N2)
Summary

| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy E(RB3LYP) | -109.52412868 a.u |
| RMS Gradient | 0.00000060 a.u. |
| Point Group | D∞h |
| Item | Value | Threshold | Converged? | |
|---|---|---|---|---|
| Maximum | Force | 0.000001 | 0.000450 | YES |
| RMS | Force | 0.000001 | 0.000300 | YES |
| Maximum | Displacement | 0.000000 | 0.001800 | YES |
| RMS | Displacement | 0.000000 | 0.001200 | YES |
.LOG File: Media:HC2616_N2_OPTF_POP.LOG
Nitrogen (N2) |
Vibrations and IR
Because N2 is linear, it uses thE 3N-5 rule, implying there is one vibrational mode. However, because this is a symmetric stretch, it does not produce a change in dipole, so is not detected by IR spectroscopy.
Hydrogen (H2)
Summary

| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy E(RB3LYP) | -1.17853936 a.u |
| RMS Gradient | 0.00000017 a.u |
| Point Group | D∞h |
| Item | Value | Threshold | Converged? | |
|---|---|---|---|---|
| Maximum | Force | 0.000000 | 0.000450 | YES |
| RMS | Force | 0.000000 | 0.000300 | YES |
| Maximum | Displacement | 0.000000 | 0.001800 | YES |
| RMS | Displacement | 0.000001 | 0.001200 | YES |
.LOG File: Media:HCHAUHAN H2 OPTF POP.LOG
Hydrogen (H2) |
Vibrations and IR
Because H2 is linear, it uses thE 3N-5 rule, implying there is one vibrational mode. However, because this is a symmetric stretch, it does not produce a change in dipole, so is not detected by IR spectroscopy.
Energy of the Haber-Bosch Process
N2 + 3H2 -> 2NH3
___________________________________________________
E(NH3)= -56.55776873 Ha
2*E(NH3)= -113.1155375 Ha
E(N2)= -109.52412868 Ha
E(H2)= -1.17853936 Ha
3*E(H2)= -3.53561808 Ha
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -146.48 kJmol-1
____________________________________________________
The energy released when converting 3 moles of hydrogen gas and 1 mole of nitrogen to gas is calculated to be -146.48 kJmol-1 based on the values calculated by Gaussview.
This implies that 1 mole of ammonia is more stable than 3 moles of hydrogen and 1 mole of nitrogen.
However, this only takes into account the electronic energies and ignores molecular vibrations. In reality, this reaction will be less exothermic than 146.48kJmol-1 due to molecular vibrations.
Silanone (H2SiO)
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy E(RB3LYP) | -365.90001403 a.u. |
| RMS Gradient | 0.00000941 a.u. |
| Point Group | C2v |
| Item | Value | Threshold | Converged? | |
|---|---|---|---|---|
| Maximum | Force | 0.000023 | 0.000450 | YES |
| RMS | Force | 0.000009 | 0.000300 | YES |
| Maximum | Displacement | 0.000023 | 0.001800 | YES |
| RMS | Displacement | 0.0000017 | 0.001200 | YES |
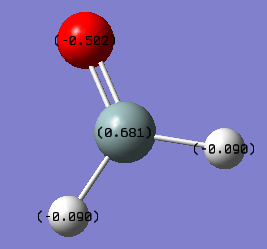
Due, to silicon's having alower electronegativity than both oxygen and hydrogen, it has a positive charge of 0.681. Oxygen draws most of the electron density, giving it a charge of -0.502 and the two hydrogen atoms each have a charge of -0.90.
Silanone(H2SiO) |
.LOG File: Media:HCHAUHAN_H2SIO_OPTF_POP.LOG
Molecular Orbitals


The 3rd MO is formed from only the 2s atomic orbital on the central silicon atom. It is too low in energy to interact with other atomic orbitals on other atoms.
The 9th MO is a bonding orbital formed from in the in-phase overlap of p-orbitals on the oxygen and silicon atom and the H2 LGO. The hydrogen atoms have a large contribution to this MO due to their contributing atomic orbitals being closer in energy to this MO than the p-orbitals on the silicon and oxygen.
The 11th MO is a π bonding orbital formed from the in-phase overlap of the px orbitals on the silicon and oxygen. The hydrogen atomic orbitals have no contribution to this MO as they do not have the correct symmetry.
The 12th MO is the HOMO and is formed from a d-orbital on the silicon atom, interacting in-phase with the H2 LGO. The px also has some contribution to this MO.
The 13th MO is the LUMO and is the anti-bonding orbital of the 11th MO. It is formed from the out-of-phase overlap between the p-orbitals on the silicon and oxygen atoms. Again the hydrogen atoms have no contribution because they are no of the correct symmetry.
Vibrations and IR Spectrum
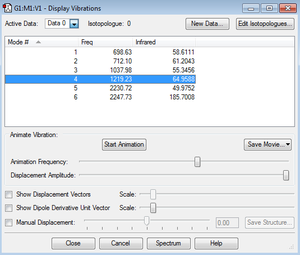
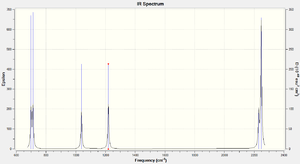
Based on the predicted absorption frequencies by Gaussview, 6 peaks should appear in the IR spectrum of H2SiO, at frequencies of 699, 712, 1038, 1219, 2230 and 2247 cm-1. This is in agreement with the 3N-6 rule for the number of vibrational modes. Furthermore, all vibrations produce a relatively large change in dipole thus, have relatively high absorbance.