Rep:Mod:HB2515Transitionstates
Introduction:
A potential energy surface (PES) is a representation of the variation of the potential energy in all dimensions. The PES possesses 3N-6 dimensions, where multiple local minima (stable intermediates) and local maxima (which define transition states) can be found. These extremum points are located by taking the first and second derivatives in all dimensions. The minimum with the lowest energy can be found, corresponding to the most stable form of the molecule, also called the thermodynamic product. In these calculations, many different conformations giving energy minima will be studied. Most of the time they are found from the same transition state (endo and exo products for example) of a reaction.
As a reaction occurs, the energy oscillates around the minimum energy pathway in the PES plot. At any minimum, the first derivative is 0, and the second derivative is positive (positive curvature, with positive force constants). This mathematical description symbolises a point at with, if deviated from in any direction, the energy will increase. At the transition state, the energy is is at the maximum of the lowest energy pathway, with a first derivatives of 0 and negative second derivatives (negative curvature, all positive force constant but one, a negative force constant, which represents the reaction pathway). Therefore the transition state can be thought of as the maximum of the minimum energy pathway.
Nf710 (talk) 16:41, 9 February 2018 (UTC) you need to be careful and make sure you are talking in 3N-6 dimensions. You can also get the Force constants by finding the eigenvalues of the hessian matrix.
In this experiment, the energies are calculated using optimised structures (where the energy of the structures are minimised). These optimised structures which also resemble the transition state are then used to locate the exact transition states and their energies. Two different calculation methods are used:
-the semi-empirical method PM6, where the the program makes guesses with pre-programmed data to accelerate the process of calculating the terms of the Hamiltonian, making more approximations resulting in less accurate results.
Nf710 (talk) 16:41, 9 February 2018 (UTC) Its is based on the HF hamiltonian.
-the B3LYP method used which uses the Density functional theory (DFT) to calculate all the terms of the Hamiltonian, resulting in slower, but more accurate technique.
Nf710 (talk) 16:41, 9 February 2018 (UTC) It is a DFT method which accounts for the electron correlation with a Hartree fOCK CALCULATION.
It is possible to obtain these results using 3 different approaches:
-The first calculation method, which requires good knowledge of the transition state. The fragments are drawn in the Gaussview software, with lots of care for the inter-nuclear distances. This structure must be extremely close to the transition state or else the optimisation might lead to another minimum, or simply not converge. The Gaussian program is then run to optimise the structure to the transition state. This method is extremely fast, and it is very practical for simple calculations.
-The second method requires more knowledge about the transition state. The fragments are placed as closely to the transition state as possible, before freezing the bonds involved in the reaction. The rest of the structure is then separately optimised to an energy minimum. The output file is then used to optimise to the transition structure. The method is slightly longer than the previous one, but the advantage is that it is more reliable and less knowledge is required about the transition state.
-Finally the last method used starts from the known product structure, which has been optimised to an energy minimum, and the transition state is found by breaking the bonds involved in the reaction and playing around with the distance between these atoms. once the structure is close enough (which should not be too challenging as the product often resemble the transition state), the structure is optimised to a transition state. This technique is longer, but it is the most reliable of all 3 and transition states of reaction where not much is know about the way the molecules come together or separate can be found.
Exercise 1: Cycloaddition of butadiene and ethene
(Fv611 (talk) Well done in this section overall but be careful when labelling your Jmols - you have marked your TS as "Product" in the table)
Molecular orbitals of the transition state
In this exercise, a [4+2] cycloaddition between ethene and butadiene is studied (see Fig. 1)

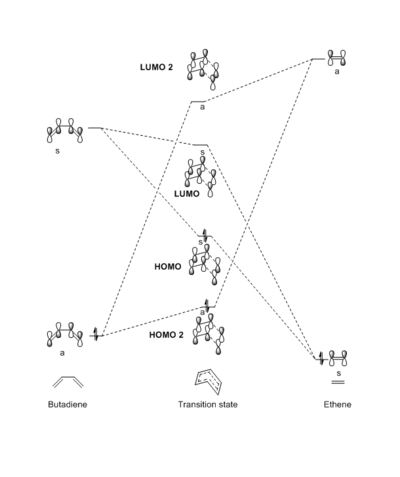
By observing the orbitals in Gaussview, it is clear which orbitals interact with each other in the transition state. These orbitals are displayed in the table below (Table 1). From this it is possible to identify the molecular orbital diagram (Fig. 2).
The HOMO and LUMO of the transition state are formed from the interaction between the LUMO of butadiene and the HOMO of ethene. They are both symmetric (s) fragment orbitals and give a symmetric molecular orbitals. There is also an interaction between the HOMO of butadiene and the LUMO of ethene (both anti-symmetric, a) giving 2 anti-symmetric molecular orbitals (2nd HOMO; HOMO 2 and 2nd LUMO; LUMO 2). This observation gives rise to a rule, only orbitals of the same symmetry can interact, resulting in identical symmetry molecular orbitals. Therefore the reaction will only proceed (reaction allowed) if there is a possible interaction of identical symmetry fragment orbitals. The overlap integral of the orbitals is 0 for symmetric/anti-symmetric combinations, and non-zero for symmetric-symmetric or anti-symmetric/anti-symmetric interactions.
The differences in energy of these orbitals arises from the the activation energy (barrier energy) required to reach the transition state, resulting in a higher energy molecular orbitals of the transition state. The amount of contribution to each molecular orbital is explained by how close the it is in energy to the fragment orbitals or the reactants. Following this logic, the HOMO 2 has a greater contribution from the HOMO of butadiene and the LUMO 2 has a greater contribution from the LUMO of ethene. Naturally the HOMO of the transition state has a higher contribution from the HOMO of ethene, and the LUMO of the transition state has a higher contribution of the LUMO of butadiene.
|
|
|
| ||||||||||||
|
|
|
|
Table 1: Illustration of the molecular orbitals of ethene, butadiene and the cyclohexene product
Bond length analysis
| Ethene | Butadiene | Transition state | Hexene | Change in bond length | |
|---|---|---|---|---|---|
| C1-C2 | 1.327 | - | 1.382 | 1.535 | Lengthens |
| C2-C3 | - | - | 2.114 | 1.537 | - |
| C3-C4 | - | 1.333 | 1.380 | 1.501 | Lengthens |
| C4-C5 | - | 1.471 | 1.411 | 1.337 | Shortens |
| C5-C6 | - | 1.333 | 1.380 | 1.501 | Lengthens |
| C6-C1 | - | - | 2.116 | 1.537 | - |
Table 2: Lengths of the Carbon-Carbon bonds throughout the reaction (In Angstroms)
| Carbon atom | Change in hybridisation |
|---|---|
| 1 | sp2 → sp3 |
| 2 | sp2 → sp3 |
| 3 | sp2 → sp3 |
| 4 | no change |
| 5 | no change |
| 6 | sp2 → sp3 |
Table 3: Change in hybridisation of the carbon atoms
As it can be observed in Tables 2 and 3, as the bond gains sp3 character (only one sp3 carbons either side of the bond to two), the bond lengthens.
In this case, the C4-C5 remains with two sp2 carbons either side, but the bond becomes shorter. This is due to the fact that the electron density was previously delocalised over multiples double bonds. Now that it is localised to that one bond, the bond is more electron rich and therefore becomes shorter (and stronger).
In the reaction state, the C2-C3 and C6-C1 have lengths inferior to two times the Van der Waal radius of the carbon atom (1.7 A). This proves that the carbon atoms are starting to interact in the transition state, before forming a single covalent bond in the product.
A typical C-C bond length is 1.54 A(1). A typical C=C bond length is 1.333 A(2). This is consistent with the lengths of the bonds in cyclohexene, but the single bond adjacent to the C=C bond are shortened from the electron density being slightly shortened due to higher electron density (again giving stronger bonds).
Transition state vibrations
The vibration illustrated above corresponds to the negative vibration of the transition state. It is negative due to the negative force constant in the transition state as mentioned earlier. The 2 bonds are formed in a concerted manor, as seen in this vibration. This is what defines a pericyclic reaction, such as this cycloaddition. This observation is confirmed in the IRC analysis.
The log file of the optimised (pm6) cyclohexene transition state here
The log file of the IRC here
The log file of the optimised (pm6) cyclohexene product here
Exercise 2: Cycloaddition of Cyclohexadiene with 1,3-Dioxole
In this part, a [4+2] cycloaddition between ethene and butadiene is studied. Below is a reaction scheme:
Molecular orbital analysis
The rule or identical symmetry as in exercise 1 is maintained in this reaction. In this molecular orbital diagram (Fig 4., see below) the LUMO of the cyclohexadiene and the HOMO of the 1,3-dioxole are the closest in energy to the transition state LUMO/HOMO. This is an inverse electron demand Diels-Alder reaction. The difference in energy of these fragment orbitals is due to the electron donating groups (lone pair on each oxygen atom) donating into the double bond on the dienophile (which should normally be electron poor). This effect results in higher energy HOMO and LUMO, making it closer in energy to the LUMO of the cyclohexadiene. There is a large energy difference between the HOMO of cyclohexadiene and the LUMO of the dienophile, making the interaction between these orbitals relatively small.
Nf710 (talk) 16:52, 9 February 2018 (UTC) How have you have managed to come to this conclusion?
Molecular orbital diagram of the reaction:
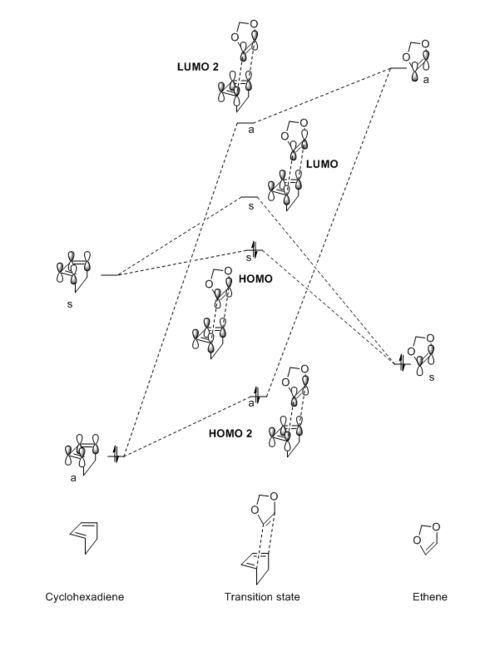
|
|
|
| ||||||||||||
|
|
|
|
Table 4: Illustration of the molecular orbitals of cyclohexadiene, 1,3-dioxole and the endo and exo products
Thermochemistry
| Product | Reaction barrier/kJmol-1 | Reaction energy/kJmol-1 |
|---|---|---|
| Endo | 159.81 | -67.40 |
| Exo | 167.64 | -63.80 |
Table 5: Reaction barrier ernergy and Free energy of the endo and exo pathways
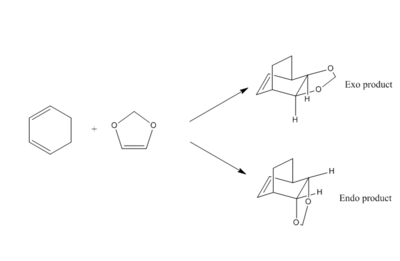
The data from the output of the log file in Gaussian was used to calculate the energies of the different intermediates. It was observed that the endo TS has a small activation barrier (see table 5 above). The endo product would be formed faster, being the kinetic product. This can be qualitatively explained by orbital overlap, stabilising the transition state; the p orbital on the oxygen atom overlaps with the conjugated pi system on the diene. The exo product does not benefit from any orbital interaction lowering its energy in the transition state, which explains the higher activation barrier.
When accounting for the energies of the products, the endo product has a lower energy than the exo conformer. The endo product is therefore considered the thermodynamic product. The reasons for this have not been completely proven, but it can be hypothesised that the same explanation for the more stable transition state can be used in the product, with the oxygen orbitals still overlapping with the pi orbitals. Furthermore, this product is a bridgehead, and the carbon chain could be repelling with the oxygen's in the exo product, however in the endo product, they are further apart. So this could be rationally explained using a steric argument as well.
The log file of the optimised (b3lyp) dioxole reactant here
The log file of the optimised (b3lyp) diene reactant here
The log file of the optimised (b3lyp) endo transition state here
The log file of the optimised (b3lyp) exo transition state here
The log file of the optimised (b3lyp) endo product here
The log file of the optimised (b3lyp) exo product here
Exercise 3: Reaction of o-Xylylene with SO2
Molecular orbitals of the transition state
In this exercise, the reaction between o-xylylene and SO2. This reaction reveals to be more complex than anticipated, as there are 5 different outcomes possible: 2 different Diels-Alder reactions and a Chelotropic reaction. Using the previous techniques, it is possible to calculate the likelihood of each pathway, and give an idea of how the reaction conditions may be used to aim for a more thermodynamic or more kinetic product.
(Well, there is actually another cheletropic pathway Tam10 (talk) 14:38, 4 February 2018 (UTC))
First we will study the reaction between the SO2 and the non-cyclic diene part of o-xylylene. The possible outcomes are illustrated in the scheme below (Fig. 5).
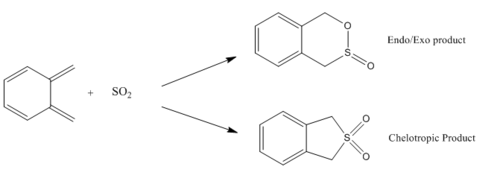
It is evident looking at the reaction scheme to the left that a large driving force will be the rearomatisation of the benzene ring, which will result in a very stable product, despite the entropy cost of the reaction.
IRC analysis
 |
 |
 |
Figure 6: IRC analysis of the transition states of the first 3 possible outcomes
These IRC calculations are useful to visualise the reaction as they proceed, with the different initial orientations of the SO2 explaining the endo and exo Diels-Alder reaction variation. When forming the 6-membered rings in the transition states, it is observed that the the oxygen bonds before the sulfur in the endo and exo reactions, but that in the 5-membered ring formation for the chelotropic product, this is simultaneous, which is expected as the 2 new bonds are formed to the same atom in the sulfur substrate.
Thermochemistry
| Product | Reaction barrier/kJmol-1 | Reaction energy/kJmol-1 |
|---|---|---|
| Endo | 81.53 | -99.26 |
| Exo | 85.50 | -99.92 |
| Chelotrpic | 103.85 | -156.24 |
Table 6: Reaction barrier energy and Free energy of the endo, exo and chelotropic reactions
As previous, these calculations were performed using the LOG output file from the Gaussian program.
The kinetic product is found to be the endo product, which is consistent with the previous observations made about the endo transition state being more stable due to the orbital overlap with the p orbital on the oxygen and the pi system on the diene. This interaction affects the more sensitive transition state of the endo product, whilst still stabilising the product. But in this case the product stabilisation is not very strong, and the endo product is the last stable of all 3. The exo product could be slightly more stable due to a less strained arrangement (flat molecule with all the atoms as far apart as possible).
(What do you mean by "sensitive transition state"? Tam10 (talk) 14:38, 4 February 2018 (UTC))
The chelotropic product is the slowest forming product, as it has the highest energy barrier (see table 6.). This is due to the formation of a strained 5-membered ring in the transition state, compared to the formation of strain free 6-memebered rings in the other reaction pathways. It is the lowest energy product, therefore the most stable, also called the thermodynamic product. this is due to the formation of strong S=O and S-C bonds, compared to just S-O and C-O bonds for the endo/exo products.
The log file of the optimised (pm6) o-xylylene reactant here
The log file of the optimised (pm6) SO2 here
The log file of the optimised (pm6) endo product here
The log file of the optimised (pm6) endo transition state here
The log file of the optimised (pm6) exo product here
The log file of the optimised (pm6) exo transition state here
The log file of the optimised (pm6) chelotropic product here
The log file of the optimised (pm6) chelotropic transition state here
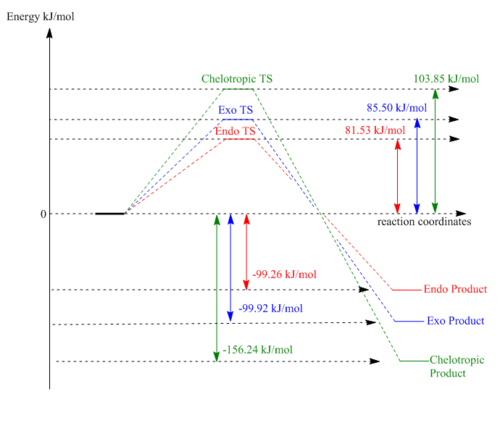
(A clear reaction profile, but you don't need to specify the units twice Tam10 (talk) 14:38, 4 February 2018 (UTC))
Alternative reaction
o-Xylylene can undergo a Diels-Alder cycloaddition to in diene in the cyclic ring as well. This is an additional pathway, which is illustrated in the IRC calculations below (Fig. 8). When calculating the energy barrier and the reaction energy, it is observed that these pathways are not very favorable. The reaction required lots of energy be performed, and,the products that are formed are not very stable compared to the starting material. This reaction does not form a highly stable aromatic ring, so as it is a competing reaction, this pathway would no be very probable at all.
| Product | Reaction barrier/kJmol-1 | Reaction energy/kJmol-1 |
|---|---|---|
| Endo | 111.74 | -16.02 |
| Exo | 119.58 | -20.47 |
Table 7: Reaction barrier energy and Free energy of the endo and exo pathways of the alternative pathways
 |
 |
Figure 8: IRC analysis of the alternative pathway reactions
The log file of the optimised (pm6) endo transition state here
The log file of the optimised (pm6) endo product here
The log file of the optimised (pm6) exo transition state here
The log file of the optimised (pm6) exo product here
Extra work:
4n Electrocyclic reaction:
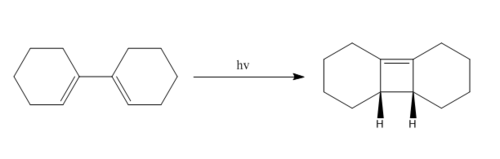
(You're not using light in this reaction. All reactions we've done are on the ground state, not on the electronically excited state. However, the barrier is likely to be smaller on the excited state. Even though you mention this later on, it's a bit confusing to see this diagram with the thermal IRC below Tam10 (talk) 14:44, 4 February 2018 (UTC))
| reactant | TS | product | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LUMO |
|
|
| |||||||||
| HOMO |
|
|
|
Using the Woodward-Hoffmann rules would predict a thermal 4 pi conrotatory stereochemical outcome. This reaction proceeds photochemically, therefore an electron is promoted to the LUMO before the reaction takes place. When looking at the LUMO of the reactant in the table above, it is clear that a disrotatory reaction would lead to the product. The product would have a new pi system which would resemble the HOMO of the product in the table above. These orbitals therefore illustrate and confirm the disrotatory mechanism that needs to take place for this photochemical reaction to proceed.
(This reaction is actually a bit tricky, as orbitals will be swapping throughout the reaction, as well as the electronic states. This makes the analysis more difficult compared to previous sections. These systems also suffer hugely when calculated with single-reference calculations such as DFT and HF Tam10 (talk) 14:44, 4 February 2018 (UTC))
(+6%)
Conclusion:
Computational chemistry has become an important tool to model synthetic chemistry. It provides good approximations, which can then be verified in the lab. A very high degree of accuracy can be obtained using the B3LYP method, but more time to perform the calculations is required, and more processing power. No doubt that this will become readily available in the near future, proving computational chemistry to be potentially an even more important part of chemical research. In this experiment, an introduction to these methods is provided using simple cycloaddtion reaction to model the possible outcomes of each possibility, and to give valuable information on the transition state. This is particularly interesting due to the fact that these transition states can not be isolated and studied in the physical world. These calculation also explain the differences in the orbital interactions in an inverse electron demand Diels-Alder reaction and provide thermochemistry data to differentiate between the endo and exo products. Finally these techniques can be used on other pericyclic reactions, as seen in the extension, when using Gaussian to explain the observation of a photochemical electrocyclic reaction.
References:
(1) Brown, LeMay & Bursten. Chemistry The Central Science. Upper Saddle River, NJ: Simon & Schuster, 1997: 227, 412-413
(2) L. S. Bartell and R. A. Bonham, J. Chem. Phys., 1959, 31, 400–404.
