Rep:Mod:H4jera
In this lab, Gaussian was used to optimise molecules and analyse their bond lengths, vibrations, charges and final energies when the molecule is in equilibrium. The parameters used to confirm the molecule was in equilibrium are shown in the "Item" table. For each molecule, an interactive Jmol file has been uploaded to display the molecule in the calculated lowest energy state.
NH3 Molecule
An NH3 molecule was constructed and optimised. The final energy obtained is later used in a calculation of the enthalpy change of the Haber process.
Details
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy, E(RB3LYP): -56.55776873 a.u.
RMS gradient: 0.00000485 a.u.
Point group: C3V
Bond length: 1.01798 Å
Bond angle: 105.741 degrees
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
NH3 molecule |
The optimisation file is linked to here
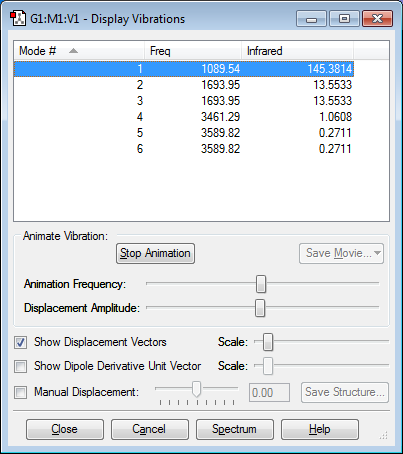
Vibrations
Expected number of modes: 3x4-6 = 6
Degenerate modes: 2 and 3 ; 5 and 6
Bending vibrations: 1, 2 and 3
Bond stretch vibrations: 4, 5 and 6
Mode number 4 is highly symmetric.
The "umbrella" mode is mode number 1.
In an experimental spectrum of gaseous ammonia I would expect 2 absorption peaks; mode one gives an intense peak of 145, and the degenerate modes 2 and 3 combine to give a smaller peak of 27. Compared to these absorptions, modes 4, 5 and 6 will not appear to absorb significantly. This is because the change of dipole moment in these modes is very small.
Charge Analysis
Charge on N: -1.125e
Charge on H: +0.375e
I would expect the N atom to have the negative charge as it is more electronegative than H. The charge on the H is expected to be positive and overall cancel out the charge on N.
N2 and H2
The individual properties of N2 and H2 were analysed. Then, the enthalpy change of the reaction when the two collide, as in the Haber process, was calculated using the final energies of the N2, H2 and NH3 molecules.
N2
Details
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy, E(RB3LYP): -109.52412868 a.u.
RMS gradient: 0.00000060 a.u.
Point group: D∞h
Bond length: 1.10550 Å
Bond angle: Linear diatomic molecule
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
N2 molecule |
The optimisation file is linked to here
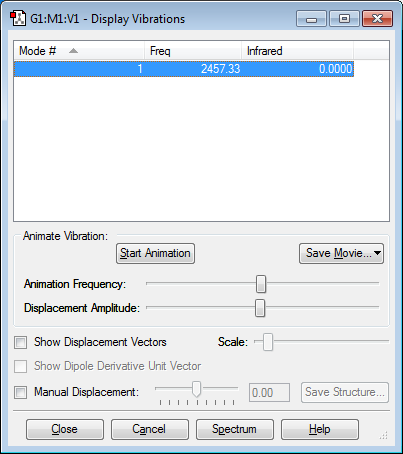
Vibrations
Only one mode is expected as diatomic molecules can only stretch symmetrically. There is no absorption as the molecule has no dipole moment.
Charge Analysis
As this is a symmetrical diatomic molecule both atoms will have a charge of zero.
H2
Details
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy, E(RB3LYP): -1.17853936 a.u.
RMS gradient: 0.00000017 a.u.
Point group: D∞h
Bond length: 0.74279 Å
Bond angle: Linear diatomic molecule
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
H2 molecule |
The optimisation file is linked to here
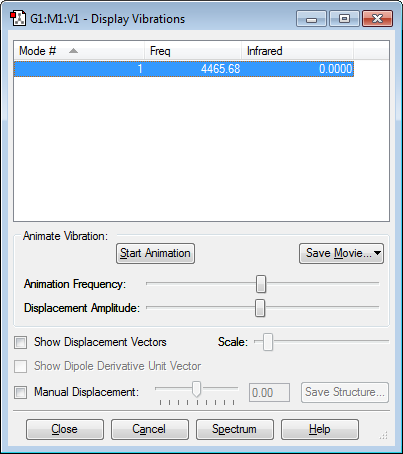
Vibrations
Again, only one mode is expected as diatomic molecules can only stretch symmetrically. There is no absorption as the molecule has no dipole moment.
Charge Analysis
As this is a symmetrical diatomic molecule both atoms will have a charge of zero.
Reaction Energy
For the reaction N2 + 3H2 -> 2NH3
E(NH3)= -56.55776873 a.u.
2*E(NH3)= -113.1155375 a.u.
E(N2)= -109.52412868 a.u.
E(H2)= -1.17853936 a.u.
3*E(H2)= -3.53561928 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.0557895 a.u.
ΔE = -0.0557895 a.u. * 2625.5 = -146.48 kJmol-1
The enthalpy change of the forwards reaction is negative therefore the ammonia product is more stable than the gaseous reactants as the products have less energy than the reactants.
[Extension] Compared to a literature value found by JM Modak (Resonance, September 2002, Volume 7, Issue 9, pp 69-77) of -91.4kJmol-1, this is quite different. This could be due to the bonds broken being stronger than calculated by Gaussian, or the bonds formed are weaker than predicted. Another factor is that there is a great decrease in entropy in this reaction; 4 moles of gas create 2 moles of gas. Therefore some energy is lost as a result of this, which Gaussian has not accounted for.
Small molecule: P2
The molecule which was chosen was P2 (diphosphorus) which is a diatomic molecule. It is analogous to N2 and H2 in terms of having only one vibration mode and no charge. Five of the molecular orbitals have been chosen and displayed below.
Details
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy, E(RB3LYP): -682.68894541 a.u.
RMS gradient: 0.00000180 a.u.
Point group: D∞h
Bond length: 1.90444 Å
Bond angle: Linear diatomic molecule
Item Value Threshold Converged? Maximum Force 0.000003 0.000450 YES RMS Force 0.000003 0.000300 YES Maximum Displacement 0.000004 0.001800 YES RMS Displacement 0.000006 0.001200 YES
P2 molecule |
The optimisation file is linked to here
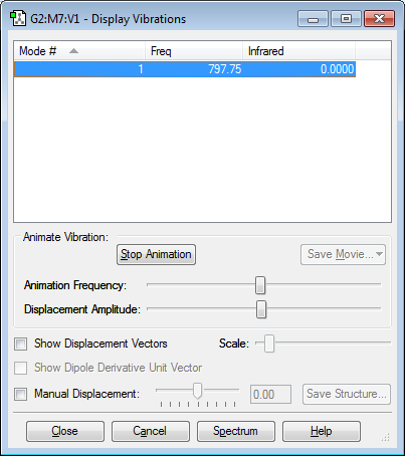
Vibrations
Only one stretching mode is expected as this is a diatomic molecule so it can only stretch symmetrically.
Charge analysis

Both phosphorus atoms have a charge of 0. This is because each atom draws the electron density equally due to being the same atom.
Molecular Orbitals
 Defined in this image to the left are the co-ordinate axes referred to below.
Defined in this image to the left are the co-ordinate axes referred to below.
Figure 1 shows the electron density of the 2s orbitals are localised on the atoms and don't interact with the other atom because they are very low in energy. These is a filled non bonding molecular orbital.
Figure 2 shows the 2px and 2py orbitals on each atom do not overlap with the other atom and do not contribute to the bonding of the molecule because they are deep in energy. It is clear that there is no contribution to the bonding of the molecule as the filled bonding and anti-bonding molecular orbitals (shown by MO numbers 5-8 on the right side panel) are all degenerate.
The 2pz orbitals shown in figure 3 have a slight overlap however there is little bonding character to this, as the energy of -4.73908 a.u. is very similar to the wholly non-bonding molecular orbitals 5-8 which have an energy of -4.74123 a.u. This is a filled MO.
Figure 4 displays the 3π bonding molecular orbitals formed from the overlap of 3px and 3py orbitals. These degenerate MO's are the highest energy filled MO's, evident from the right-side panel, which makes this the HOMO of the molecule.
Figure 5 indicates the 3π* anti-bonding molecular orbitals which accompany the 3π bonding orbitals and so are also formed from the 3px and 3py orbitals. They are not filled with electrons, and are the LUMO.