Rep:Mod:Ginger3
In this module I will be characterise transition structures on potential energy surfaces for the Cope rearrangement and Diels Alder cycloaddition reactions. This will be carried out by using molecular orbital based methods, numerically solving the Schrodinger equation and locating transition structures based on the local shape of a potential energy surface to show what transition structures look like and then calculating reaction paths and barrier heights.
The Cope Rearrangement Tutorial
In this section I will be investigating the Cope rearrangment of 1,5-hexadiene which is a [3,3]-sigmatropic shift rearrangment. It is generally accepted that the mechanism occurs in a concerted fashion via the "chair" or "boat" transition structure with the "boat" being higher in energy. I will therefore locate the low-energy minima and transition structure on the C6H10 potential energy surface to determine the reaction mechanism that is preferred.
Optimising the Reactants and Products
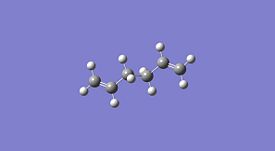
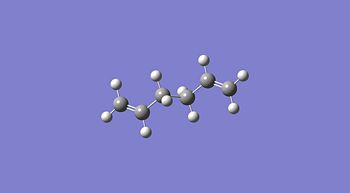
1,5-hexadiene was drawn on ChemBio3D in the anti conformer, this was then imported into GaussView and the structure was cleaned. This was then optimised using the HF method and 3-21G basis set. This was then repeated in the gauche conformer and the results obtained are shown below. This method and basis set used is reasonably accurate and achieves results in a reasonably quick time unlike more complex methods and basis sets.
| Property | Anti Conformer[1] | Gauche Conformer[2] | Lowest Energy Conformer[3] |
| Jmol |  |
 |
 |
| Calculation Type | FOPT | FOPT | FOPT |
| Calculation Method | RHF | RHF | RHF |
| Basis Set | 3-21G | 3-21G | 3-21G |
| Charge | 0 | 0 | 0 |
| Spin | Singlet | Singlet | Singlet |
| E(RHF) | -231.69254 a.u. | -231.69167 a.u. | -231.69266 a.u. |
| E | -608308.7514 kJ/mol | -608306.5000 kJ/mol | -608309.0800 kJ/mol |
| RMS Gradient Norm | 0.00001933 a.u. | 0.00003890 a.u. | 0.00004715 a.u. |
| Dihedral Angle | 180o | 64.2o | 67.7o |
| Dipole Moment | 0.00 Debye | 0.38 Debye | 0.34 Debye |
| Point Group | Ci | C2 | C1 |
| Specific conformer | anti 2 | gauche 2 | gauche 3 |
| Time | 1 minute 8.0 seconds | 1 minute 39.0 seconds | 47 seconds |
From the data above it can be seen that the anti conformer is lower than the gauche conformer but only by ≈2.3 kJ/mol. Upon inspection of the energies and point groups of the two conformers it can be seen from appendix 1 that the specific conformers optimised are anti 1 which has a Ci point group and gauche 2 which has a C2 point group. These energies agree with the energies in appendix 1[4].
The lowest energy conformation of a reactant molecule is used as a reference and therefore this reference is used in all calculations as the standard (enthalpy and activation energy calculations). The results above would indicate that the anti conformer will be the lowest energy conformation of 1,5-hexadiene as it will minimise the steric stain in the molecule. However with a chain molecule a degree of guache stabilises the molecule and having completely anti causes the molecule to be less favoured by entropy as it is too structured. It is therefore a mixture of the two and when the optimisation is carried it can be seen that it is at a lower energy and therefore my theory and prediction was correct.
The Ci anti conformer that I calculated above which agreed with the data in appendix 1[5], was then reoptimised using DFT and a higher level of B3LYP and the 6-31G(d) basis set. The data from the optimisation before and the reoptimisation can be seen below.
| Property | Anti 2 Conformer[6] | Anti 2 Reoptimised Conformer[7] |
| Jmol | |
 |
| Bond Angles |  |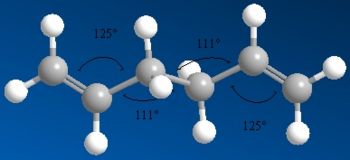
|
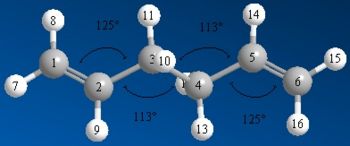
| Calculation Type | FOPT | FOPT |
| Calculation Method | RHF | RB3LYP |
| Basis Set | 3-21G | 6-31G(d) |
| Charge | 0 | 0 |
| Spin | Singlet | Singlet |
| E(RHF) | -231.69254 a.u. | -234.61170 a.u. |
| E | -608308.7514 kJ/mol | -615973.0300 kJ/mol |
| RMS Gradient Norm | 0.00001933 a.u. | 0.00001336 a.u. |
| Dihedral Angle | 180o | 180o |
| Dipole Moment | 0.00 Debye | 0.00 Debye |
| Point Group | Ci | Ci |
| Specific conformer | anti 2 | anti 2 |
| Time | 1 minute 8.0 seconds | 5 minute 36.0 seconds |
As seen above the energy for the reoptimised anti 2 the molecule is at a much lower energy with a difference of ≈7660 kJ/mol (≈2.9 a.u.) and whilst the images and jmols look identical there are some subtle differences. The double bonds in the reoptimised conformer is longer than in the originally optimised version (1.334Å compared to 1.316Å), the bonds between C2-C3 and C5-C6 are shorter in the reoptimised conformer (1.504Å compared to 1.509Å) and the central bond between C3-C4 is shorter in the optimised conformer (1.548Å to 1.553Å). The angles also have slight differences between the two optimised conformers. Overall this shows that the overall geometry does not change and that the higher optimisation just alters the structure very slightly to get a slightly more optimised structure.
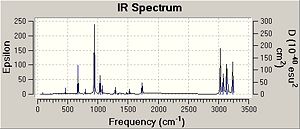
Frequency analysis was then carried out on the B3LYP/6-31G(d) optimised structure at the same level of theory. This was carried out to check that the molecule was in the lowest conformation (global minima) and was not in a local minima as in a global minima all the frequencies should be positive which they were indicating that this indeed is the lowest energy conformation of the molecule. This analysis was also carried out in order to calculate the thermodynamic data shown below:
Sum of electronic and zero-point energies = -234.469212 a.u.
Sum of electronic and thermal energies = -234.461856 a.u.
Sum of electronic and thermal enthalpies = -234.460912 a.u.
Sum of electronic and thermal free energies = -234.500821 a.u.
The sum of electronic and zero-point energies is the potential energy at 0 K including the zero-point vibrational energy. The sum of electronic and thermal energies is the energy at 298.15 K and 1 atm of pressure including the translational, rotational and vibrational energy modes. The sum of electronic and thermal enthalpies includes a correction for RT. The sum of electronic and thermal free energies includes entropic contribution to the free energy.
Optimising the "Chair" and "Boat" Transition Structures
In this section I will be setting up a transition structure optimisation using 3 different methods: by computing the force constants at the beginning of the calculation, by using the redundant coordinate editor and using QST2. Then the reaction coordinate will be visuliased, a IRC run and the activation energies for the Cope rearrangement calulated for the "chair" and "boat" transition structures. Initially a CH2CHCH2 fragment was optimised using the Hartree-Fock method and the 3-21G basis set, this was then used for further calculations.
Optimising the "Chair" Transition Structure
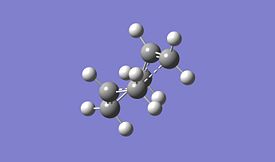
Two different methods were used for the optimisation of the "chair" transition structure, by computing the force constants at the beginning of the calculation and using the redundant coordinate editor. The computing the force constants at the beginning of the calculation involved optimising to a TS (Berny) and choosing to calculate the force constants. The redundant coordinate editor involved optimising the molecule to a minimum while keeping the two sets of two terminal carbons from the allyl fragments frozen to 2.2 Å and then setting the bonds to derivative and optimising to a transition state (Berny) therefore not using force constants. The Hartree Fock method and 3-21G basis set was used for these calculations.
| Property | Force Constants Method[8] | Redundant Coord Editor Method[9][10] |
| Jmol |  |
 |
| Calculation Type | FREQ | FREQ |
| Calculation Method | RHF | RHF |
| Basis Set | 3-21G | 3-21G |
| Charge | 0 | 0 |
| Spin | Singlet | Singlet |
| E(RHF) | -231.619322 a.u. | -231.619322 a.u. |
| E | -608116.529911 kJ/mol | -608116.529911 kJ/mol |
| RMS Gradient Norm | 0.00001294 a.u. | 0.00000634 a.u. |
| Dipole Moment | 0.00 Debye | 0.00 Debye |
| Point Group | C2h | C2h |
| Imaginary Frequency | 1 (-818 cm-1) | 1 (-818 cm-1) |
| Imaginary Frequency |  |
 |
| Bond Forming/Breaking Length | 2.02 Å | 2.02 Å |
| Time | 32.0 seconds | 32.0 seconds |
As seen in the table above the energies of the two different methods are the same, they have the same imaginary frequency, the same point group and upon visual inspection the two methods give the same structure. From the visualisation of the frequency it can be seen that this is indeed the frequency for the Cope rearrangement where one bond is breaking and one forming. It can then be induced that the two methods give the same optimised structure with the same bond forming/breaking distance and therefore the force constants method is suitable for this calculation and the redundant coordinate editor method although useful for more complex molecules is not required for this calculation.
Optimising the "Boat" Transition Structure
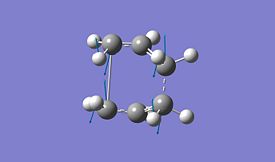
The boat transition structure was optimised using the QST2 method. This requires the reactant and product to be specified so that the program can interpolate between the two structures to find the transition state. The numbering system must then be altered for the reactant and product so that the two molecules have different numbers as shown below. The opt-freq calculation was then carried out using the TS(QST2) method at HF method and 3-21G basis set.
 |
 |
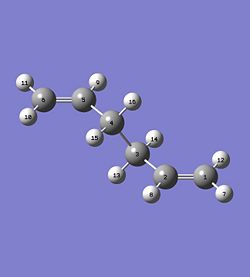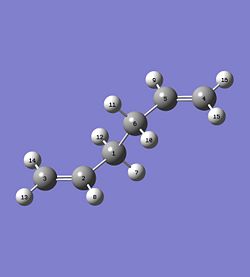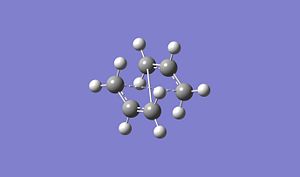
A Opt-Freq calculation was then carried out using the TS(QST2) method with the correct atom numbering[11]. This however failed and looks more like a chair structure, this is because the calculation translates the top fragment and does not rotate around the central bond. The product and reactant structures therefore must be changed for QST2 to give a reasonable transition state. The central C-C-C-C dihedral angle was changed to 0o and the inside C-C-C bond was changed to 100o, this leads to the structures below.
 |
 |
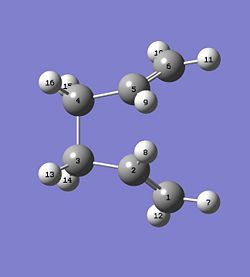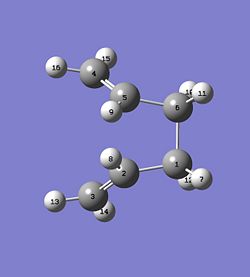The results after this geometry are shown below using HF method and 3-21G basis set[12].
| Property | Boat Transition Structure |
| Jmol |  |
| Calculation Type | FREQ |
| Calculation Method | RHF |
| Basis Set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| E(RHF) | -231.602802 a.u. |
| E | -608073.156651 kJ/mol |
| RMS Gradient Norm | 0.00002433 a.u. |
| Dipole Moment | 0.16 Debye |
| Point Group | C2v |
| Imaginary Frequency | 1 (-840 cm-1) |
| Imaginary Frequency |  |
| Bond Forming/Breaking Length | 2.14 Å |
| Time | 18.0 seconds |
As can be seen the bond length for the boat conformer is 2.14 Å which is longer than the bond length for the chair of 2.02Å. The energy of the boat transition state is also slightly lower than the energy of the chair transition state. This is because of the extra steric hinderance that is present in the boat compared to chair. There is also an imainary frequency present again which is observed to be for the Cope rearrangment as there is one bond making and one bond breaking.
Intrinsic Reaction Coordinate (IRC)
When the optimised chair and boat transition structures are modelled it is very difficult to determine what conformer of 1,5-hexadiene that will be formed, however using the IRC method it can be determined. This method allows us to follow the minimum energy path from a transition structure to its local minimum on the potential energy surface, it takes small geometry steps in the direction of the steepest gradient and creates a series of points. The chk file from the transition state optimised chair structure was opened and the IRC job type selected under the Gaussian menu, the forward recation coordinate was selected, the force constants were set as being calculated once at the start of the calculation and the number of steps chosen was 50. This however failed[13] with an error message of maximum number of corrector steps exceded, the recorrect steps was then set to always and the calculations ran to completion. The results are shown below.[14]
 |
 |
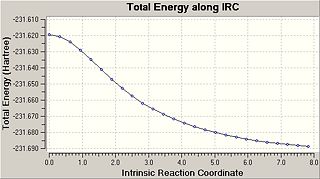As can be seen from the graph a minimum has not yet been reached and that one of three things must be carried out to reach a minimum; run a normal optimisation on the last IRC point, restart the IRC with a larger number of points or redo the IRC specifying the force constants to be recalculated at each step. Each of these types of calculations was then carried out.
A normal optimisation was carried out on the last step of the 50 step IRC using HF/3-21G method and basis set.[15] The results have an energy of -231.69167 a.u. and a point group of C2, when this is compared to the appendix 1[16] it corresponds to a gauche 2 conformer.
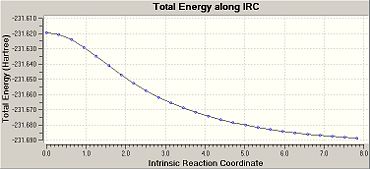
The IRC was restarted as before but this time with 150 steps instead of 50.[17] As can be seen it has an energy of -231.68863 a.u. and a point group of C2, however the IRC plot indicates that it has not achieved a complete minimum and has only achieved a local minimum.
 |
 |
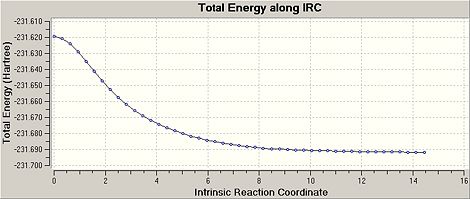
The IRC was then carried out again with 150 steps as before but with force constants recalulate at each step.[18] This has an energy of -231.69166 a.u., a point group of C2 and this is therefore a the gauche 2 conformer. The IRC plot indicates that this is a minimum as it achieves a plateau.
 |
 |
It can therefore be assumed from these calculations that the reaction creates a gauche 2 conformer and a lower energy conformer. It can also be seen that whilst caluclating force constants can be useful it it quicker to use a small number of steps caluclating the force constants once and then optimising the final IRC step and still gives similar results.
Comparison of Optimisation Levels
The activation energies were then calculated for both transition structures. This required optimisation and frequency calculations at the B3LYP method and 6-31G* basis set and at the HF method and 3-21G basis set, the results are shown below.[19][20][21][22]
 |
 |
 |
 |
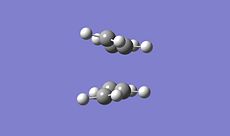As can be seen the geometries are the same however as seen below the energies do differ.
| HF/3-21G | B3LYP/6-31G* | |
|---|---|---|
| Reactant (anti2) | ||
| Sum of electronic and zero point energies at 0K (a.u.) | -231.539539 | -234.469212 |
| Sum of electronic and zero point energies at 298.18K (a.u.) | -231.532565 | -234.461856 |
| Chair Transition Structure | ||
| Sum of electronic and zero point energies at 0K (a.u.) | -231.466700 | -234.414928 |
| Sum of electronic and zero point energies at 298.18K (a.u.) | -231.461340 | -234.409009 |
| Boat Transition Structure | ||
| Sum of electronic and zero point energies at 0K (a.u.) | -231.450928 | -234.402344 |
| Sum of electronic and zero point energies at 298.18K (a.u.) | -231.445299 | -234.396008 |
The activation energy was then calculated by taking the energy of the transition structure by the energy of the reactant.
| HF/3-21G | B3LYP/6-31G* | Experimental | |
|---|---|---|---|
| Chair Transition Structure | |||
| ΔE at 0K (kcal/mol) | 45.71 | 34.06 | 33.5 ± 0.5 |
| ΔE at 298.15K (kcal/mol) | 44.69 | 33.16 | |
| Boat Transition Structure | |||
| ΔE at 0K (kcal/mol) | 55.60 | 41.96 | 44.7 ± 2.0 |
| ΔE at 298.15K (kcal/mol) | 54.76 | 41.32 |
The results above when compared with the data in appendix 2[23] agree reasonably well. The activation energies when compared with the experimental values do not agree though indicating that neither the boat or the chair transition states are modelled correctly. When the activation energies are viewed it can be seen that the chair transition state is lower than the boat transition state, this indicates that under kinetic control the reaction will proceed via the chair transition state and not the boat transition state.
The Diels Alder Cycloaddition
In this section I will characterise the transition structure of the diels alder cycloaddition of ethylene and cis butadiene and then study the regioselectivity of the diels alder reaction of cyclohexa-1,3-diene with maleic anhydride. The MOs of the cis butandiene, the transition state and the reaction of cyclohexa-1,3-diene with maleic anyhdride will also be modelled.
 |
 |
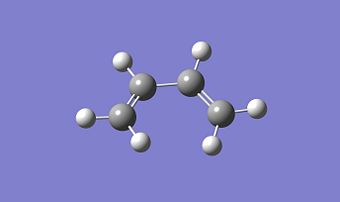
Cis Butadiene
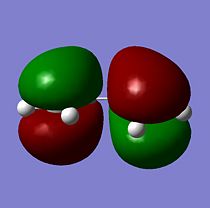
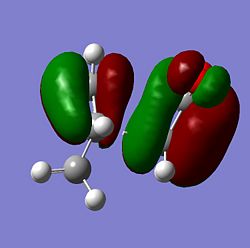
Cis Butadiene was optimised in Gaussview using HF method and 3-21G basis set[24] and then was optimised with the AM1 semi-empirical molecular orbital method[25] and the MOs of the HOMO and LUMO were visualised. These optimisations formed a planar molecule as shown below and the MOs are also shown below.
 |
 |
 |
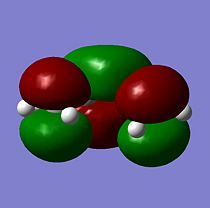The HOMO is formed from 2 p in phase orbitals on one side combining with 2 p out of phase orbitals on the other side of the molecule, this leads to a nodal plane being present with an energy of -0.34456 a.u.. Therefore the HOMO is anti-symmetrical (a) with respect to the plane. The LUMO is formed from 2 p in phase orbitals on the central carbons combining with 2 p out of phase orbitals on the outer carbons, this leads to 2 nodal planes being present with an eenergy of 0.01797 a.u.. Therefore the LUMO is symmetrical (s) with respect to the plane.
Diels Alder Transition State
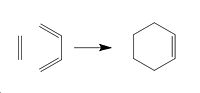
The transition state geometry of a Diels Alder cycloaddition reaction was now calculated and the nature of the reaction path examined. The optimised cis butadiene molecule from the earlier section was loaded and a ethylene group added to the molecule group, the ethylene was then orientated above the cis butadiene double bonds with a bond length of 2.1 Å set between the terminal carbons from the ethylene and the cis butadiene. This stucture was then cleaned in GaussView and the force constants method was used as it was seen earlier that it produces good results in a quick time. 2.1 Å was chosen as it is longer than a standard C-C bond but there is still significant interactions. A opt-freq calculation was then carried out using the TS (Berny) method with force contants calculated once, the additional keywords set as opt=noeigen and the semi-emperical AM1 method used. This gave the following data as seen below[26].
| Property | Transition State |
| Jmol |  |
| Calculation Type | FREQ |
| Calculation Method | RAM1 |
| Basis Set | ZDO |
| Charge | 0 |
| Spin | Singlet |
| E(RHF) | 0.111655 a.u. |
| RMS Gradient Norm | 0.00003361 a.u. |
| Dipole Moment | 0.56 Debye |
| Bond Forming/Breaking Length | 2.12 Å |
| Time | 1.0 seconds |
An IRC calculation was then carried out using the semi-emerpical AM1 method calculating in both directions, force constants set as always, recorrect steps always and 150 steps. The results can be seen below[27].
| Reactants | Transition State | Product |
 |
|
 |
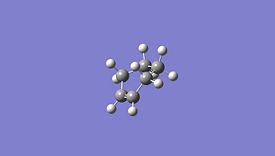| IRC Energy Plot | IRC RMS Gradient Plot | |
 |
 |
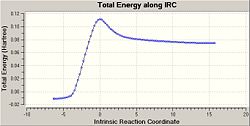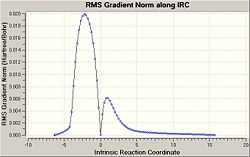As can be seen above the transition state forms the correct product and comes from the correct reactants, when the energy plot is observed it is seen that it is the highest energy and therefore a transition state has been formed especially as the bond forming/breaking length from above is 2.12 Å which is longer than a C-C bond but is still short enough for significant interactions to occur.
The cis butadiene optimisation from earlier was used and the ethylene MOs were calculated using optimisation and the semi-emperical AM1 method.[28]
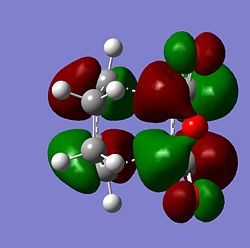
| Molecule | HOMO | LUMO |
| Cis Butadiene |  |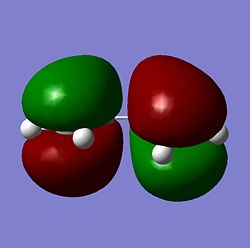
 |
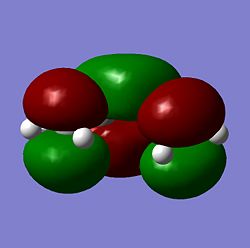| Ethylene |  |
 |
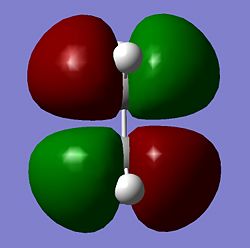| Transition State |  |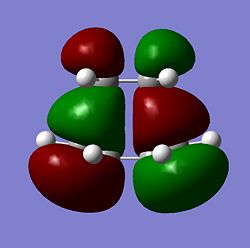
 |
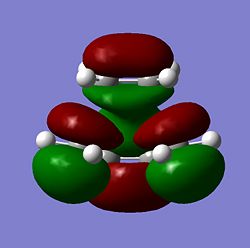As seen above the HOMO for the transition state it is anti-symmetric and the LUMO for the transition state is symmetric, the ethylene has a symmetric HOMO and an anti-symmetric LUMO, the cis butadiene has a anti-symmetic HOMO and a symmetric LUMO. It can be seen from these HOMO and LUMO that the transition state HOMO has formed from the cis butadiene HOMO and the ethylene LUMO and the transition state LUMO has formed from the cis butadiene LUMO and the ethylene HOMO. This reaction is therefore allowed as the HOMO-LUMO pairs that interact and of the same symmetry and therefore allowed forming a transition state HOMO which is anti-symmetric and a LUMO that is symmetic agreeing with how the MOs of the cis butadiene and ethelyne interact. Therefore the reaction is energetically favourble and occurs.
The van der Waals radius is 1.7 Å[29], the sp2 carbon length is 1.54 Å and the sp3 carbon length is 1.34 Å[30]. The forming carbon bond is 2.12 Å, this is longer than a normal carbon σ-bond length but is within the two carbon van der Waals radius, this indicates that whilst a carbon σ-bond has not formed there is significant interactions due to van der Waals interaction. The other carbon carbon bonds are also indicative of a transition state as C1-C2, C1-C4 and C11-C14 are all 1.38 Å whilst the C3-C4 bond is 1.40 Å; these bond lengths are between sp2 and sp3 bond lengths and therefore are in a transition state in between a double and single bond state.
The frequencies can now be analysed as shown below.
| Frequency | Image | Wavlength / cm-1 |
| Imaginary Frequency |  |
-955.91 |
| Lowest +ve Frequency |  |
147.23 |
The imarginary frequency at -955.91 cm-1 corresponds to the reaction path and is seen to be synchronous with the two bonds forming at the same time as each other. This can then be compared to the next lowest frequency at 147.23 cm-1 which involves the ethylene twisting and would lead to a concerted two step process and not the one step process as shown by the vibration at -955.91 cm-1.
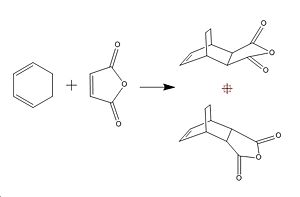
The Regioselectivity of a Diels Alder Reaction
Maleic anhydride and cyclohexan-1,3-diene undergo a diels alder reaction to form either the endo or exo product, the primary product is the endo form. This reaction should be kinetically controlled so therefore the exo transition state should be higher in energy, this will now be investigated.
Initially the endo and exo products were drawn in ChemBio3D and optimised using MM2 to give the optimised exo and endo form, this was then imported into Gaussview, the C-C bonds forming were lengthened to 2Å and the bonds were changed so that they were suitable for the transition state. A optimisation and frequency calculation was then carried out using the semi-emperical AM1 method, with Opt=NoEigen in the additional keywords, the TS (Berny) optimisation was used and force constants set to be calculated always. The results can be seen below[31][32].
| Property | Endo Transition State | Exo Transition State | |
| Jmol |  |
 | |
| Calculation Type | FREQ | FREQ | |
| Calculation Method | RAM1 | RAM1 | |
| Basis Set | ZDO | ZDO | |
| Charge | 0 | 0 | |
| Spin | Singlet | Singlet | |
| E(RHF) | -0.05150480 a.u. | -0.05041985 a.u. | |
| RMS Gradient Norm | 0.00000018 a.u. | 0.00000069 a.u. | |
| Dipole Moment | 6.17 Debye | 5.56 Debye | |
| Imaginary Frequency | -806.38 cm-1 | -812.19 cm-1 | |
| Imaginary Frequency |  |
 | |
| Bond Forming/Breaking Length | 2.16 Å | 2.17 Å | |
| Time | 4.0 seconds | 3.0 seconds |
As can be seen the imaginary frequencies present correspond with the bonding forming reaction and this is the only -ve frequency in each molecule. This therefore indicates that these molecules are the global minima for each structure and not local minima and that these are indeed transition structures.
From above it can be seen that the energy of endo transition state is lower than the exo product by a difference of 0.68 kcal/mol. This indicates that the endo form is the kinetic product as shown experimentally. The endo product has a bond forming length of 2.16 Å and the exo product forming bond is 2.17 Å, this is because of the extra steric clash between the maleic anhydride and cyclohexa-1,3-diene. This is because of the large bridge causing increased hinderance in the exo which is on the other side of the molecule on the endo and therefore there is less hinderance as for the endo there is a less bulky subsituent and therefore less hinderance.
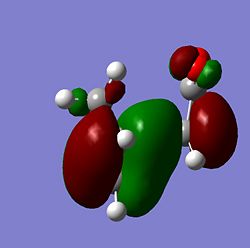
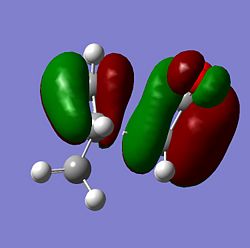
| Molecule | HOMO Side | HOMO Above | LUMO Side | LUMO Above |
| Endo |  |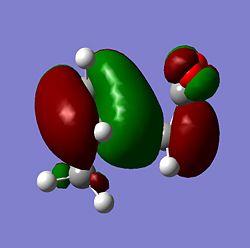
 |
 |
 |
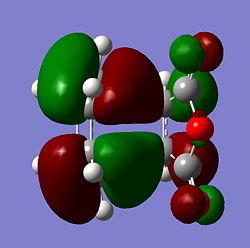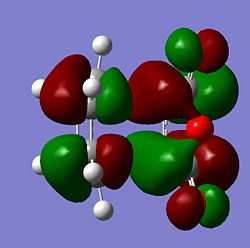| Exo |  |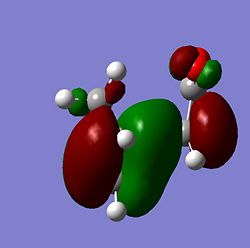
 |
 |
 |
From the MOs above it can be seen that the MOs for endo and exo have a nodal plane along the symmetry plane. Another reason for the lower energy of the endo is due to seconday orbital overlap which can be seen in the MOs. The distance between the carbons from the -(C=O)-O-(C=O)- fragment and the -CH=CH- (endo)/ -CH2-CH2- (exo) are 2.89 Å and 2.95 Å respectively. The reason for the endo being smaller is because the secondary orbital overlap effect is more prominent for the endo product and so stabilises the molecule more and so the bond is shorter. This is because there is greater aligment between the fragments and therefore there is more favourable interactions in the endo than the exo. There is also in the endo electron density on the oxygens which leads to greater secondary orbital interactions and therefore greater stability for the endo.
Therefore overall the endo product is the more kinetically stable product and the major product during experimental conditions.
References
- ↑ https://www.ch.ic.ac.uk/wiki/index.php/Image:CopeAntiConformer.LOG
- ↑ https://www.ch.ic.ac.uk/wiki/index.php/Image:CopeGaucheConformer.LOG
- ↑ https://www.ch.ic.ac.uk/wiki/index.php/Image:CopeLowestEnergyConformer.LOG
- ↑ http://www.ch.ic.ac.uk/wiki/index.php/Mod:phys3#Appendix_1
- ↑ http://www.ch.ic.ac.uk/wiki/index.php/Mod:phys3#Appendix_1
- ↑ https://www.ch.ic.ac.uk/wiki/index.php/Image:CopeAntiConformer.LOG
- ↑ https://www.ch.ic.ac.uk/wiki/index.php/Image:CopeAnti2HigherOptimisation.LOG
- ↑ https://www.ch.ic.ac.uk/wiki/index.php/Image:ChairTSForceConstantsMethod.LOG
- ↑ https://www.ch.ic.ac.uk/wiki/index.php/Image:ChairTSBondFrozen.LOG
- ↑ https://www.ch.ic.ac.uk/wiki/index.php/Image:ChairTSBondUnfrozenDerivative.LOG
- ↑ https://www.ch.ic.ac.uk/wiki/index.php/Image:BoatTSFailure.LOG
- ↑ https://www.ch.ic.ac.uk/wiki/index.php/Image:BoatTS_Successful.LOG
- ↑ https://www.ch.ic.ac.uk/wiki/index.php/Image:IRC_50Steps_Error.out
- ↑ https://www.ch.ic.ac.uk/wiki/index.php/Image:IRC_50Steps_Successful.out
- ↑ https://www.ch.ic.ac.uk/wiki/index.php/Image:ChairOptimisedAfter50StepsofIRC.LOG
- ↑ http://www.ch.ic.ac.uk/wiki/index.php/Mod:phys3#Appendix_1
- ↑ https://www.ch.ic.ac.uk/wiki/index.php/Image:IRC_150Steps.out
- ↑ https://www.ch.ic.ac.uk/wiki/index.php/Image:Chair_IRC150Steps_ForceConstantsCalulatedAlways.out
- ↑ https://www.ch.ic.ac.uk/wiki/index.php/Image:ChairTS_HF3-21G.LOG
- ↑ https://www.ch.ic.ac.uk/wiki/index.php/Image:ChairTS_B3LYP6-31Gd.out
- ↑ https://www.ch.ic.ac.uk/wiki/index.php/Image:BoatTS_HF3-21G.LOG
- ↑ https://www.ch.ic.ac.uk/wiki/index.php/Image:BoatTS_B3LYP6-31Gd.LOG
- ↑ http://www.ch.ic.ac.uk/wiki/index.php/Mod:phys3#Appendix_2
- ↑ https://www.ch.ic.ac.uk/wiki/index.php/Image:Butadiene321GOptimisation.LOG
- ↑ https://www.ch.ic.ac.uk/wiki/index.php/Image:ButadieneAM1Optimisation.chk
- ↑ https://www.ch.ic.ac.uk/wiki/index.php/Image:DielsAlderTransitionStateForceConstantsMethod.chk
- ↑ https://www.ch.ic.ac.uk/wiki/index.php/Image:JonPDielsAlderIRC150.fchk
- ↑ https://www.ch.ic.ac.uk/wiki/index.php/Image:EtheneOptimisation.chk
- ↑ http://www.ccdc.cam.ac.uk/products/csd/radii/
- ↑ http://www.science.uwaterloo.ca/~cchieh/cact/c120/hybridcarbon.html
- ↑ https://www.ch.ic.ac.uk/wiki/index.php/Image:GingerEndo_attempt_1.chk
- ↑ https://www.ch.ic.ac.uk/wiki/index.php/Image:GingerExo_attempt_1.chk