Rep:Mod:Gcf14ts
Introduction
This computational lab involves the location and characterisation of transition states of Diels-Alder reactions using Gaussian.
A minimum on a potential energy surface is a place where the curvature of the surface is equal to zero (ie where the total gradient is equal to zero). A transition state is a maximum on the potential energy surface (where the total gradient is also equal to zero).
To distinguish between a minimum and a transition state on the potential energy surface, the second derivative can be examined. In the case of a minimum, the second derivative will be positive; for a transition state, the second derivative will be negative.
Nf710 (talk) 19:37, 21 March 2017 (UTC) This a good explanation but in electronic structure methods we are working in higher dimensions you have only said one here.
Methods of calculating the Transition State
There are three main methods for calculating a transition state in Gaussian. The first method involves providing a guess transition state which is then optimised. This is the fastest method of calculating a transition state, but can only be used when you have a good knowledge of the transition state.
The second method, which was used for the first two exercises, also involves providing a guess transition state. However, in this method, the reacting atoms are frozen. The structure is then minimised, before being optimised to the transition state. This method is more reliable than the first method, because when the bonds are frozen, the remainder of the structure is minimised and so it is closer to the transition state before the transition state is calculated.
The third method, used in exercise 3, starts from the product. The product was optimised, and then suitable bonds and angles were changed to form the transition state. The reacting atoms were subsequently frozen, and the structure minimised again. Finally, the structure was optimised to the transition state. This method is the most reliable method.
Computational Methods [1]
Calculations were run at two different computational levels - PM6 and B3 LYP level. The PM6 level is semi-empirical in nature, and so uses less computational power, but the results are not as accurate. However, it is good to use when dealing with larger numbers of atoms.
B3 LYP uses a combination of density functional theory (DFT) and Hartree Fock theory for the electron configuration. It is traditionally used with the 6-31(G) basis set. The results are better than PM6, but it uses more computational power (scales at N3), where N is the number of atoms.
Exercise 1: The reaction of butadiene with ethylene
This reaction is a simple example of a 4+2 cycloaddition, commonly termed Diels-Alder reaction.
The molecular orbital diagram for the formation of the transition state is shown in figure 1.

(Fv611 (talk) 17:35, 15 March 2017 (UTC) Good MO diagram, but you have not drawn the relative energy levels in scale with the energy values you calculated.)
Both the reactants and the transition state were optimised at the PM6 level. The HOMO and LUMO of the reactants were visualised as well as the orbitals that the combinations of these produce in the transition state. These are depicted in the table below.
The butadiene HOMO combines with the ethylene LUMO to form the antisymmetric bonding and antibonding orbitals. The symmetric bonding and antibonding orbitals are formed from the combination of the butadiene LUMO and the ethylene HOMO.
For a reaction to occur, the orbitals which are overlapping must have the same symmetry (ie. must either both be symmetric of antisymmetric). If this is not the case, then the reaction is forbidden. For the case of symmetric-symmetric interactions and antisymmetric-antisymmetric interactions, the overlap integral is non-zero. In the case of a symmetric-antisymmetric interaction, the orbital overlap integral is equal to zero.
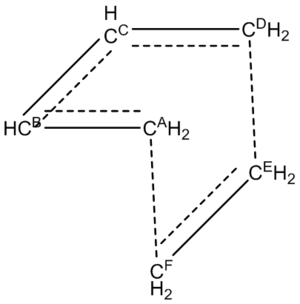
The bond lengths in both the reactants and the transition state are shown in the tables below.
| C-C Bond | Bond Length /Angstroms |
|---|---|
| CA-CB | 1.335 |
| CB-CC | 1.468 |
| CC-CD | 1.335 |
| CE-CF | 1.327 |
| C-C Bond | Bond Length /Angstroms |
|---|---|
| CA-CB | 1.380 |
| CB-CC | 1.411 |
| CC-CD | 1.380 |
| CE-CF | 1.382 |
| CA-CF | 2.114 |
| CD-CE | 2.114 |
As the reaction progresses, the CA-CB and CC-CD bond lengths increase in length (from 1.335 angstroms in the reactants to 1.380 angstroms in the transition state). The CE-CF bond length (from the ethylene molecule) also increases (from 1.327 angstroms in the reactants to 1.382 angstroms in the transition state). The increase in length of these bonds is expected, because in the reactants they are all double bonds, and in the transition state these double bonds are in the process of being broken to form the single bonds found in the product.
The CB-CC bond length decreases as the reaction progresses (from 1.468 angstroms in the reactants to 1.411 angstroms in the transition state). This is because in the transition state, this bond has partial double bond character, resulting in the shortening of the bond.
The typical C-C sp3 and sp2 bond lengths are 1.54 and 1.34 angstroms respectively. [2]. The distance between the 2 carbon atoms where the new bond forms is 2.11 angstroms in the transition state. The Van der Waals radius of a carbon atom is 1.7 angstroms[3]. This implies that these two carbon atoms are interacting with one another as they are within 2 Van der Waals radii of one another.
The vibrations that display the reaction path at the transition state are illustrated in Jmol 1. The formation of the bonds in this reaction is synchronous, as both of two new bonds between the reactants and the products are formed simultaneously. If the reaction were asynchronous, the bonds would be formed in two individual steps, and the mechanism would most likely be diradical in nature.
Exercise 2: the reaction of cyclohexadiene and 1,3-dioxole

This is another example of a Diels-Alder reaction. However, unlike the previous example, there are two possible products of this reaction: the exo and the endo product. They are formed depending on the orientation of the reacting fragments. The structures of these two products are shown in figure 3.
From the previous MO diagram (figure 1), the occupied and unoccupied MO's for both transition states have been found by symmetry and are shown on this page.
The MO diagram for the transition state of this reaction is shown below.

(Nice and clear diagram. It might be worth mentioning whether the example here is endo or exo Tam10 (talk) 10:35, 23 March 2017 (UTC))
The relative energies of the reactant fragment orbitals were found by doing a single point energy calculation on the IRC file of the transition state. From these relative energies, it is possible to infer whether the reaction is a normal Diels-Alder or and inverse electron demand Diels-Alder. This is an inverse electron dmenad Diels-Alder, as the LUMO is based on the diene, and the HOMO is based on the dienophile. This is the criteria for an inverse electron demand Diels-Alder.
Thermodynamics
The energies of the reactants, products and transition states were found from the .log files. These are tabulated below.
| Reactant energies /kJmol-1 | Exo Transition State energy /kJmol-1 | Endo Transition State energy /kJmol-1 | Exo Product energy /kJmol-1 | Endo Product energy /kJmol-1 |
|---|---|---|---|---|
| -1313781.985 | -1313614.32 | -1313622.165 | -1313845.779 | -1313849.376 |
| Exo Reaction Barrier /kJmol-1 | Exo Reaction Energy /kJmol-1 | Endo Reaction Barrier /kJmol-1 | Endo Reaction Energy /kJmol-1 | |
| 167.6644428 | -63.79440385 | 159.8194482 | -67.39133913 |
The kinetically favoured product is the endo product, as the reaction barrier is lower (159.8 kJmol-1 as opposed to 167.7 kJmol-1 for the exo reaction). The exo product is the thermodynamic product, as there are fewer unfavourable steric interactions in the exo product compared to the endo product. These steric interactions mean that the endo product is higher in energy, and therefore not the thermodynamic product.
Nf710 (talk) 19:48, 21 March 2017 (UTC) No! you have correctly calculated that the endo is both. -67 is a bigger difference than -63.
Secondary orbital effects
The reaction barrier energy can be affected by secondary orbital interactions, and is the reason why the endo reaction has a lower reaction barrier. Orbitals on the oxygen atoms (p orbitals) interact with orbitals on the dienophile, resulting in the transition state being stabilised and therefore lower in energy. [4]. These stabilising interactions can only occur in the endo transition state. These secondary orbital interactions can be seen in the Jmols here.
Nf710 (talk) 19:50, 21 March 2017 (UTC) A diagram would have been good here. You calculated the energies correctly but came to the wrong conclusion.
Exercise 3: Diels Alder vs Chelotropic reaction

The reaction between ortho-xylylene and SO2 can either progress as a Diels-Alder reaction, with the potential of forming exo or endo products, or it could progress as a chelotropic reaction. These reactions are shown in figure 5.
A chelotropic reaction differs from a Diels-Alder pericyclic reaction as for one of the reagants, both new bonds are formed to the same atom. In this example, both new bonds are formed to the sulfur atom.
The transition states for the exo, endo and chelotropic reactions were optimised at the PM6 level. The reaction coordinates for each of the reaction pathways were visualised by an IRC calculation. These are shown below.

|
| Visualisation of exo Diels-Alder reaction path |

|
| Visualisation of endoDiel-Alder reaction path |

|
| Visualisation of chelotropic reaction path |
From the IRC's, it can be seen that during the course of the reaction, the original 6 membered ring from the xylylene reactant fragment becomes similar to benzene (as it gains a double bond), and forms a planar ring. This formation of this aromatic ring is therefore the driving force for the reaction.
Thermodynamics
| Exo Reaction Barrier /kJmol-1 | Exo Reaction Energy /kJmol-1 | Endo Reaction Barrier /kJmol-1 | Endo Reaction Energy /kJmol-1 | Chelotropic Reaction Barrier /kJmol-1 | Chelotropic Reaction Energy /kJmol-1 |
|---|---|---|---|---|---|
| 85.61493602 | -99.8057646 | 81.63467772 | -99.18089556 | 103.9724334 | -156.1306204 |
(This table can be restructured to make it more readable by grouping exo, endo and chelotropic in one axis and barriers and reaction energies in another Tam10 (talk) 10:35, 23 March 2017 (UTC))
The thermodynamic data is also illustrated in a reaction profile in figure 6, shown below.

(Don't use smooth lines! The gradients are not zero at your reactants or products so the diagram looks incomplete. Simple straight lines between stationary points means you are not making assumptions about the gradient Tam10 (talk) 10:35, 23 March 2017 (UTC))
Of the two Diels-Alder reactions, the endo reaction has the lower activation energy, as a result of having secondary orbital interactions which lower the energy of the transition state. Therefore, this is the kinetic product, whilst the exo reaction is the thermodynamic product. The chelotropic reaction has a very high activation energy barrier, however is the most thermodynamically stable product.
Second Butadiene Fragment
There are two butadiene fragments in o-xylylene. Therefore, it is plausible that a Diels-Alder reaction can occur at the position of the second butadiene fragment (which is situated inside the ring). Both the exo and the endo reactions at this butadiene fragment are thermodynamically and kinetically unfavourable. This can be seen by examining the thermodynamic data shown below.
| Exo Reaction Barrier /kJmol-1 | Exo Reaction Energy /kJmol-1 | Endo Reaction Barrier /kJmol-1 | Endo Reaction Energy /kJmol-1 |
|---|---|---|---|
| 119.6913031 | 20.57341957 | 111.8515595 | 16.12582223 |
Both reactions have high reaction barriers, when compared to the Diels-Alder reaction at the other butadiene fragment, and the products of both are less stable than the reactants. Therefore, the reaction at the second butadiene fragment is unfavourable. Unlike the Diels-Alder reaction on the other butadiene fragment, there is no aromaticity in the final product to drive the reaction. Therefore, a Diels-Alder reaction is unlikely to occur at this second butadiene site.
Conclusion
Three different reactions were investigated in this experiment, with calculations being run at the PM6 and B3lyp/6-31G(d) level. Of the three potential methods that could have been used to find the transition state, method 2 was used for exercise 1 and 2, with method 3 being used for exercise three. The third method is the most comprehensive method, whilst the first method is the least useful as it relies on having a good knowledge of the transition state and its geometry.
Of the two calculation levels, B3lyp/6-31G(d) gave better results, as PM6 is semi-empirical in nature and so is less accurate due to the approximations used. However, it uses less computational power, and so is useful when only a qualitative analysis of transition state and reactant energies is required.
In exercises 2 and 3, the endo product was the kinetic product, as a result of a stabilised transition state (due to secondary orbital interactions), whilst the exo product was the thermodynamic product.
References
- ↑ The Handbook of Medicinal Chemistry: Principles and Practice, A. Davis, S.E. Ward, The Royal Society of Chemistry, 2015, pp71
- ↑ Chemistry Data Book, J.G Stark, H.G Wallace, John Murray Ltd, 1980, pp31
- ↑ A. Bondi, J. Phys. Chem, 1964, 68(3), pp 441-451
- ↑ Organic Chemistry, J. Clayden, N. Greeves, S. Warren, Oxford University Press, Oxford, 2nd Edn., pp885








