Cope Rearrangement

The aim of this section is to find stable conformations of 1,5-hexadiene and the transition state of the 1,5-hexadiene cope rearrangement shown below. The [3,3] sigmatropic shift likely proceeds with a concerted mechanism. As the transition state would be in effect a six membered ring two main conformations are envisaged, the chair and the boat form.

Reactants and Products

Different conformations of 1,5-hexadiene were optimised using Gaussian. Several different conformational minima were identified and they are reported in the table below along with their relative energies. All of the structures shown below were calculated at the HF/3-21G level of theory.

It was expected that the gauche conformer would be higher in energy as the larger groups should have been furthest away from each other minimising any unfavourable steric interactions. This hypothesis was in agreement with the first two calculations which showed the gauche conformer as slightly higher in energy.

**Different Conformers of 1,5-Hexadiene**
Energy\hartree	Relative Energy\kJmol^-1	Point Group	Identified As
-231.69097057	4.44	C1	Anti 4
-231.68961575	7.99	C1	Gauche 5
-231.69266114	0.00	C1	Gauche 3
-231.691667	2.59	C2	Gauche 2
-231.69260229	0.16	C2	Anti 1
-231.69253529	0.33	Ci	Anti 2

The lowest energy structure was therefore expected to be an anti conformer however a slightly more stable gauche conformer was found. An MO analysis of the gauche 3 conformer HOMO (below) shows that there is a small amount of overlap between the alkene pi orbitals. The resulting electronic stabilisation lowers the energy of the gauche conformer below that of the anti conformers.

Further analysis was carried out on the Anti 2 product obtained above. The molecule was re-optimised this time using DFT B3LYP method with the 6-31G(d) basis set. The resulting structure is shown below. As can be seen there is very little difference between the two geometries despite the large (~13kJmol^-1) energy difference.

**Anti 2 Conformer**
Molecule
Energy\hartree	-234.61171035
Symmetry	Ci
Alkene Stretch\cm^-1	1731
Alkene C-H Stretch\cm^-1	1134
IR Spectrum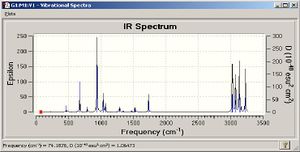

A frequency analysis was carried out on optimised molecule. No negative frequencies were reported indicating that the molecule had been optimised to a minimum. Two of the vibrational modes are reported above along with the IR spectrum generated. Thermochemistry data produced in the output file of the calculation is reported below. Using the ReadIsotopes keyword and by appending the following code to the bottom of the input file the vibrational analysis was carried out at 0K. There will almost certainly be a difference in these values if calculated at 298.15K as the isotopic mass entered was only to one decimal place.

  blank line
0.0 1.0
12.0 [six times for carbon atoms]
1.0 [ten times for hydrogen atoms]
  blank line

**Thermochemistry Data at 198.15K**
Parameter	B3lYP 6-31G\hartree
Sum of electronic & zero point energies	-234.469204
Sum of electronic & thermal energies	-234.461857
Sum of electronic & thermal free enthalpy	-234.460931
Sum of electronic & thermal free energy	-234.500779

**Thermochemistry Data at 0K**
Parameter	B3lYP 6-31G\hartree
Sum of electronic & zero point energies	-234.468767
Sum of electronic & thermal energies	-234.461430
Sum of electronic & thermal free enthalpy	-234.460486
Sum of electronic & thermal free energy	-234.500330

The first term is supposed to be calculated for 0K in both cases (as electronic temperature and zero-point energy are unaffected by temp) the change observed here suggests that changing the mass of the isotopes messed up this energy.

Chair Transition State

Two methods were used to locate and optimise the chair transition state shown below. The first involves computing force constants at the beginning of each calculation step to find the sign of the potential energy surface; the second method optimised all parts of the molecule other than the reaction coordinate (atoms with bonds forming/breaking) before the first approach is applied. All calculations were carried out at the HF/3-21G level of theory unless otherwise specified.

An allyl fragment was created and optimised (shown below). To produce a guess of the transition state two copies of the fragment were orientated so that:

The two fragments were parallel;
The terminal carbons were eclipsing each other when viewed perpendicular to the plane of the fragments;
The spacing between the fragments was 2.2 Å;
The fragments were pointing in the same direction

Method One

The guessed transition state described above was optimised to a transition state by selecting optimise to a TS(Berny) which produced opt=ts in the input file. The keywords Opt=NoEigen was used to ensure that the calculation would not crash if more than one negative frequency were encountered in the frequency analysis that was running concurrently. The option "calculate force constants once" was specified which added opt=(calcfc,ts) to the input file command line. The results of the calculation are shown below.

Transition State
Energy\hartree	-231.61932241
Imaginary Vibration Frequency\cm^-1	-818
Inter Fragment Distance\Å	2.02

It can be seen the the optimisation has reduced the distance between the terminal carbons to 2.01 Å and twisted the fragments away from each other. Only one negative vibration was observed confirming that the structure found was a transition state. The vibrational mode shown above clearly corresponds to the cope rearrangement with bonds that break stretching and bonds that form have atoms "colliding" in the right places.

Method Two

The same starting geometry was used for this method. Using the "redundant coordinate editor in gaussview 5 both pairs of terminal carbon atoms were set as a "bond" and and had their coordinates frozen this caused Opt=ModRedundant and a code telling Gaussian which atoms were frozen to be added to the input file. The fragments were optimised to a minimum. The geometry looked the same as the previous transition state except that the distance between the fragments was still set to 2.20 Å. In the redundant coordinate editor the atoms were set to "Bond" and "Derivative" this again added Opt=(modredundant) and a code to the input file. An optimisation was now run in the same way as method one but with force constants never being calculated. The transition state obtained is shown below.

Transition State
Energy\hartree	-231.61932240
Imaginary Vibration Frequency\cm^-1	-818
Inter Fragment Distance\Å	2.02

The transition state has a very similar geometry to the one obtained before.

Boat Transition State

The optimised structure of the Anti 2 conformer was duplicated to create a two molecule "group" in gaussview. The two molecules were then orientated in the same way and had their atom numbers changed so that one molecule was the result of the cope rearrangement on the other, as shown below. A transition sate optimisation and frequency analysis were carried out using the QST2 method which interpolates between the two molecules. The keyword Opt=NoEigen was also used.

Transition State
Energy\hartree	-231.60279912
Imaginary Vibration Frequency\cm^-1	-839
Inter Fragment Distance\Å	2.14

If run with the first geometries shown below the calculation ends in an error. With central C-C-C-C dihedral angle set to 0 degrees and the inside C-C-C angle at 100 degrees so that the molecules look like the second example below the transition state shown below is reached.

Intrinsic Reaction Coordinate

It's impossible to tell which conformer will be formed by the transition state from eye alone. Thus an Intrinsic Reaction Coordinate calculation was run on both transition state isomers to find which conformer was preferred. The calculation follows the reaction profile by letting the geometry fall down the steepest slopes of the potential energy surface. As the cope rearrangement is symmetrical the IRC is calculated in only one direction.

Boat

The IRC was run with up to 200 points and the force constant being calculated once. However the IRC path terminated after 20 points without the molecule reaching a minimum. The calculation was resubmitted with force constants now being calculated at every step. This calculation ran for 100 steps and took 35min (a much longer time than the simple optimisation method described below). The geometry produced, however is very similar to the lowest energy Gauche 3 conformer described above. The energies also suggest the conformers are the same.

**Geometry Resulting from IRC**
Geometry
Uploaded Log File	Media:BOAT_IRC_ALWAYS.LOG
Energy\hartree	-231.69265786
Energy Difference To Gauche 3\kJmol^-1	0.0086

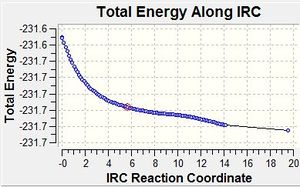
Chair

The IRC was calculated again with upto 200 points and force constants calculated once but again the calculation took only 22 points and did not fully optimise the molecule as shown below. An optimisation to a minimum was made and the following geometry which corresponds to the Anti 2 conformer above, which is not the lowest in energy.

**Optimised Structure**
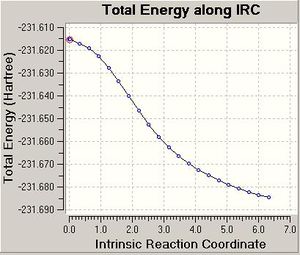Structure
Energy\hartree	-231.69253523
Symmetry	Ci

Activation Energies

The transition states obtained above were re-optimised using the DFT B2LYP/6-31G* level of theory and new frequency calculations were carried out. The results of which are shown below. The differences between the geometry of the molecules is unrecognisable but there is a significant difference in energy, which, as expected is lowered when a better basis set is used.

**Results of Higher Level Calculations**
Transition State	Geometry	Energy\hartree
Chair		-234.55698301
Boat		-234.5409307

**Thermochemistry**
Parameter	Chair 298.15K	Chair 0K	Boat 298.15K	Boat 0K
Electronic and Zero Point Energies	234.414927	234.414483	234.402342	234.401903
Electronic and Thermal Energies	234.409005	234.408573	234.398007	234.395580

The activation energies reported below are the difference between the thermodynamic quantity reported in the log file of the transition states (reported above) and the quantity from the Anti2 conformer. The activation energy at 0K is based on the difference between the "sum of the electronic and zero point energies" which is the energy of the molecule at 0K (where no translation, vibrations or rotations are possible) and the energy at 298.15K is based on the "sum of electronic and thermal energies" which includes all terms.

**Activation Energies\kcalmol^-1**
Geometry	@ 0K	@298.15K	Experimental (0K)
Chair	34.06	33.17	33.5
Boat	41.93	41.32	44.7

The results above show that the calculations predict the experimental results with a good degree of accuracy. The chair transition state is predicted to the most stable of the two with, if the error on the calculations is taken to be small and the results accurate enough, both chair and boat transition structures lowering in energy as the temperature increases.

Diels Alder Reactions

Ethylene & Butadiene Cycloaddition

This section investigates the Diels-Alder cylcloaddition of the the diene ethylene with the dienophile cis butadiene. The reaction is shown below.

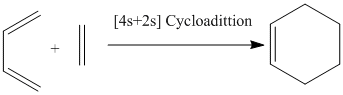
Butadiene

A molecule of cis butadiene was optimised using the semi-emprical method AM1 to give the geometry shown below. The keyword pop=full was used and the MOs of the molecule were visualised and the HOMO and LUMO are shown below.

The symmetry of the orbitals can be considered with respect to the plane of symmetry bisecting both molecules. The HOMO of butadiene is antisymmetric along with the LUMO of ethylene and the LUMO of butadiene is symmetric along with the HOMO of ethylene. This shows that all HOMOs can interact with all LUMOs.

Addition

The transition state of the addition was calculated using the first method used on the chair transition state above, where the geometry of the transition sate is guessed and then optimised. The transition state is shown below, it was estimated to be the geometry producing the biggest overlap of pi orbitals required for the reaction and the gap between molecules was chosen as it was likely to be similar to the transition states calculated above. An optimisation was carried out using the the semi-empirical AM1 approach, the transition state was confirmed with vibrational analysis.

**Transition State Facts**
Structure
Energy\hartree	0.11165
Imaginary Vibration\cm^-1	-956

It is clearly seen from the MO diagrams above the the LUMO is symmetric while the HOMO is antisymmetric. As the bonding interaction of orbitals will not change the symmetry this suggests that the HOMO is formed by the interaction of the HOMO on Butadiene with the LUMO on ethylene, this shows that the diene is acting as the nucleophile and thus we have normal (as opposed to inverse) electron demand. The LUMO has the symmetry to be formed by the bonding interaction of the other MOS and looks like them as well. These interactions are allowed as the MOs that are interacting have the same symmetry and thus a large overlap.

**Bond Lengths**
Bond	Length	Partially formed C-C bond between molecules	2.18Å
Typical C-C bond length	1.54Å
Typical C=C bond lengths	1.47Å
Carbon Vdw radius	1.70Å

This shows that the interacting atoms are well within each others sphere of influence but have not reached the equilibrium position bond lengths, which is pretty much in the definition of a transition sate.

Bond formation symmetrical with both bonds being formed at the same time. The lowest energy positive vibration was a bending of all many bonds in the structure.

Cyclohexa-1,3-diene & Maleic Anhydride Cycloaddition

The [4s+2s] cycloaddition of cyclohexa-1,3-diene & maleic anhydride can proceed with two transition states to give two regioisomers. The transition states shown below were first characterised using the semi-empirical AM1 method to optimise to a transition state from a guess, then reoptimised using the DFT B3LYP\ 6-31G(d) method. The HOMOs and LUMOs of the reactants are shown below:

Endo Transition State

**Endo Transition State**
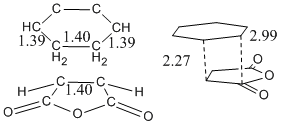Structure
Energy\Hartree	-612.68339678
Imaginary Vibration\cm^-1	-447

Exo Transition State

**Exo Transition State**
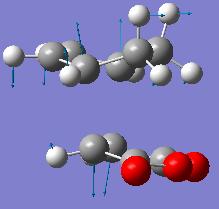Structure
Energy\Hartree	-612.67931096
Imaginary Vibration\cm^-1	-449

Its useless/ to compare the transition state activation energy as the energy of the reactants is affected by spacial relationship to each other. The relative energies of the transition states show that the Endo transition state is 2.56 jcalmol^-1 lower in energy than the exo.

The exo form is likely more strained as the two fragments are further apart and there is less chance for a small stabilising interaction, however this is not seen in the transition state MOs (due to the symmetry effects described below?) so it must be a steric repulsion which doesn't make sense if the gap is bigger.

The endo HOMO has its O=C-O-O-C=O fragment out of phase with the rest of the molecule both parts are anti-symmetric, the LUMO is also anti-symmetric along with the rest of the molecule. The exo HOMO is out of phase with the rest of the molecule and again both parts are anti-symmetric.

No secondary orbital overlap effects are observed