Rep:Mod:GD409 module3
Module 3: Modelling of Transition States
Introduction
In this computational module the Cope Rearrangement will be analysed by optimising the reactants, products and transition states to see what the most favourable mechanism is. The molecular orbitals are calculated and the frequencies. Thermodynamic data is also looked at along with structural parameters and IRC energy paths. The same kind of analysis is performed for the Diels Alder cycloaddition. At the very end using all the skills learned from different base sets the regioselectivity of the reaction between cyclohexa-1,3-diene and maleic anhydride is examined.
The Cope Rearrangement Introduction
During this rearrangement a sigma bond breaks and another sigma bond forms in a concerted pericyclic reaction. In this particular example 1,5-hexatriene undertakes a [3,3] sigmatropic reaction. The transition state is either in the chair or boat conformation. The aim of the experiment is to calculate the most stable optimised structure for the transition states, reactants and product in order to define the lowest energy mechanism for the reaction. The prediction is that the boat transition state has a higher energy than the chair according to Maluendes. Numbers are assigned to the migrating atoms which are labelled in both structures involved. [1]
Optimising reactants and products
There are four gauche/synclinical and six antiperiplanar conformations for 1,5-hexadiene formed by changing the double bond positioning in relation to the main middle carbon atoms. The structures were optimised with gaussview5.0 using the Hartree Fort me with the 3-21G base set.
In 1,5-hexadiene the central atoms are sp3 hybridised. The experimental data show that the gauche conformation is less stable than the anti-periplanar. This can be explained by σC-H/σ*C-H interactions of antiperiplanar orbitals, VDWs forces and bond-bond repulsions. The VDWs stabilise the gauche while the Pauli repulsions favour the anti-periplanar.
On the contrary to the discussed anti-periplanar favourable interactions and the experimental results the lowest energy confromation obtained is the 3rd gauche one that has an energy -231.6927au. A possible reason might be that the anti-periplanar stabilisation might not be as strong as the pi orbital overlap possible between the double bonds in the gauche. This may lower the energy for the gauche. Due to the insignificatnly small differences in energy between anti1, anti2 and gauche3 it cannot be conclusively confirmed which is more stable. The anti is only very slightly higher in energy.
Below is the HOMO of the gauche3 conformer which illustrates pi-pi interaction (shown by the red shading):
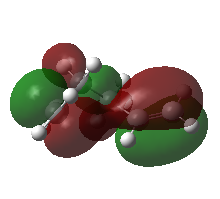
This pi-pi interaction contributes to making it the most stable (most negative). DOI:10042/to-12572
| Structure | 3D | Jmol | Point group | Energy/ kJmol-1 | DOI | Relative Energy kcalmol^-1 |
| Gauche1 |  |
C2 | -231.6877 | DOI:10042/to-12350 | 3.10 | |
| Gauche2 |  |
C2 | -231.6917 | DOI:10042/to-12351 | 0.62 | |
| Gauche3 |  |
C1 | -231.6927 | DOI:10042/to-12460 | 0.00 | |
| Gauche4 |  |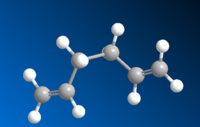
C2 | -231.6915 | DOI:10042/to-12352 | 0.71 | |
| Gauche5 |  |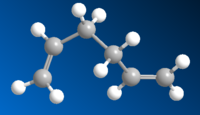
C1 | -231.6896 | DOI:10042/to-12353 | 1.91 | |
| Gauche6 |  |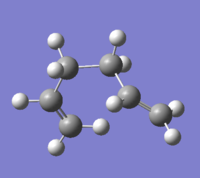
C1 | -231.6892 | DOI:10042/to-12571 | 2.20 | |
| Anti1 |  |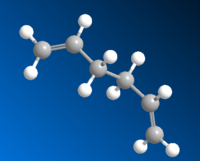
C2 | -231.6926 | DOI:10042/to-12354 | 0.04 | |
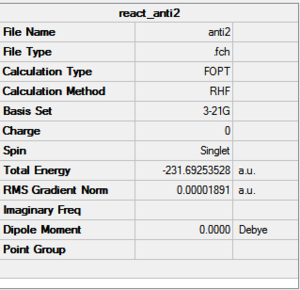
| Anti2 |  |
Ci | -231.6925 | DOI:10042/to-12355 | 0.08 | |
| Anti3 |  |
C2h | -231.6891 | DOI:10042/to-12356 | 2.25 | |
| Anti4 |  |
C1 | -231.6910 | DOI:10042/to-12357 | 1.06 |
The relative energies show that the gauche3 has the lowest (0) energy which agrees with the energy result. Realative to each other gauche1> anti3> gauche6> gauche5> anti4> gauche4> gauche 2> anti2 > anti1> gacuhe3. This is the order of least stable to the most stable.
Below are the images for the numbering and the pi interaction in gauche3:
| Aspect of structure | HF/3-21G | B3LYP/6-31G(d) | Lit value [2] |
| Energy/ Hartrees | -231.69253 | -234.61170 | - |
| C3-C4 (C-C bond)/ Å | 1.553 | 1.548 | 1.524 |
| C2-C3/ Å | 1.509 | 1.504 | 1.508 |
| C1=C2 (C=)/(Å) | 1.316 | 1.334 | 1.326 |
| C-H Average/Å | 1.087 | 1.095 | 1.099 |
| C2-C3-C4/ ° | 111.5 | 112.7 | 111.0 |
| C1=C2-C3 /° | 124.8 | 125.3 | 122.5 |
| C2=C1-H /° | 121.7 | 121.7 | 120.4 |
| C3-C2-H /° | 115.5 | 115.7 | 118.4 |
| H-C3-H/ ° | 107.7 | 106.7 | 107.1 |
| C2-C3-C4-C5/ ° | 180 | 1180 | -178.2 |
| C1=C2-C3-C4/ ° | 114.6 | 118.5 | 116 |
B3LYP result:
.PNG)
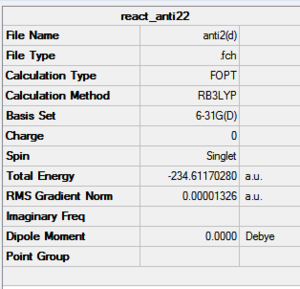
HF result:
Therefore a different basis set 6-31G(d) under DFT-B3LYP can be used to optimise the anti2 again as this includes all the electrons so although computationally more demanding, it is more accurate and should obtain a smaller energy. Obviously since the methods for calculation are different the energies cannot be compared.
The table shows that the energies are not the same as expected and as mentioned cannot be compared due to the different methods. The literature values are nearly mathcing with the calculated bond angles and lengths. As expected the more accurate B3LYP method gave values which were even more similar than the HF as the structure must be at a lower minium (most stable). Therefore better optimisation. To really test the lowest energy minimum, gain more data and improve the overall energies a 6-31G(d) base set needs to be used to calculate again the anti2 conformer. This allows energy comparison. Vibrational analysis provides proof via the second derivative that a minimum on a PES curve has actually been reached.
Sum of electronic and zero-point energies -234.46921 Sum of electronic and thermal energies -234.46186 Sum of electronic and thermal free energies G = H - TS -234.50082 Sum of thermal and electronic enthalpies H = E + RT -234.46091
The data gained here is more detailed than just a final optimised energy. It is possible to obtain the addition of the rotational, vibrational and translational energy at standard conditions. Also by using the RxT term the enthalpy can be calculated. The zero-point vibrational energy is also obtained at 0K. By taking into account entropy the free energy acquired.
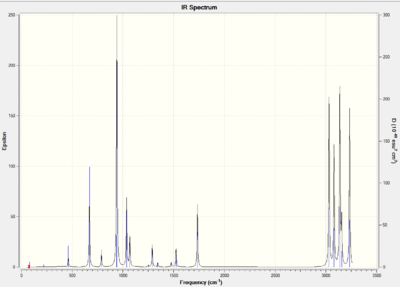
The confirmation of a minimum stationary point is shown by the positive vibrational stretches (42 in total). The C=C bond occurs at a frequency of 1731cm^-1 and bending C-H peaks at 1034,942 and 626cm^-1. The four high intensity peaks between 3031, 3080, 3137 and 3234cm^-1 occur because of the C-H stretches.
Vibrational analysis
Transition states optimisation
Chair
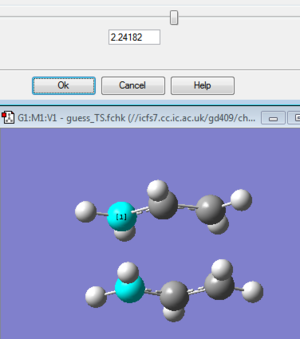
One possible method relies for the assumed structure of the TS to be nearly identical to the precise actual structure. The way this works is to calculate a force constant at the start and have gaussian optimise the TS. Two Ch2CHCH2 fragments make up the chair structure by laying them vertically above each other with a distance of 2.2Armstrong between the terminal carbon atoms. Afterwards using additional keywords for avoiding the failure of calculation due to imaginary frequencies occuring on more than one occasion throughout the optimisation, a force constant is calculated by an optimisation and frequency using HF/3-21G basis set. The results show a negative imaginary frerquency at 817.9cm^-1 which matches the simulatneous formation and breaking of sigma bonds discussed earlier. The other values obtained are for the terminal carbon atom distance of 2.02Armstrong (decreasing from 2.2 before) and the final optimised energy is -231.6193a.u.
Another method is to freeze the structure (between the terminal carbon bonds) by utilising the redundant coordinate editor. The structure was then relaxed allowing for optimisation. Here no force consntants are computed and after the bonds were altered to derivative, a TS Berny optimisation was run. The results were very similar as the terminal carbon bond distance again decreased to 2.02 Armstrong after the TS Berny optimisatipon, the energy was -231.693 a.u. and the imaginary vibrational stretch was the same as when the first method was used. DOI:10042/to-12470
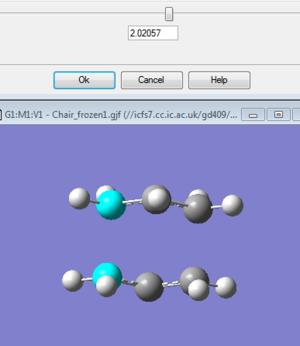
Below is the thermodynamic data for the Chair under HF optimisation+freq:
In fact the optimised structure geometries were identical for the two methods used in terms of energy, bond length and frequency. The advantage of the second method is that the force consant is not calculated so if it was more complex, the first method would suffer, whilst the second would be more useful as it relies upon differentiating the reaction coordinate. In the first method the Hessian is fully calculated whilst in the second that is unnecessary.
The imaginary frequency is when the force constants are taken for vibrations resulting from the 2nd PES derivative. The TS is the maximum along the coordinate on the PES which is from the negative 2nd derivative.
Boat
The transition state structure is resolved using the product and reactant structures and computationally implementing them. This is different to the chair as there it was drawn on gaussview by human. Two anti2 structures were placed side by side and the atoms were labelled using numbers so that the product atoms correspond to what the atoms of the reactant would be after they are reorganized. Using HF/3-21G a TS(QTS2) optimisation and frequency calculation is subsequently performed.
 |
 |
At the end a TS structure similar to a chair formed as there was little central bond free rotation which means the optimisation was unsuccessful. By using the most stable reactant and prodcut structures the TS for the boat was not obtained. Another optimisation can be performed if the C2-C3-C4-C5 dihedral angle is 0 degrees and the angles are 100 degrees for the internal C2-C3-C4 atoms.
 |
 |
 |
Below is the thermal data for the QST2 optimised boa structure:
As expected the optimisation was now correct and the optimised TS was obtained for the boat. To show that the optimisation converged a negative frequency was formed (imaginary frequency at -840.3cm^-1). In conclusion as long as the reactant and product structures to begin with are ideal the QST2 method works effectively as it is fully automated. DOI:10042/to-12490
IRC
Chair IRC
| Method | IRC originally | Optimisation with HF/3-21G basis set | 2nd Optimisation (Force constant calculated at every step) |
| Energy/Hartrees | -231.68514 | -231.69167 | -231.69166 |
| RMS Gradient/a.u. | 0.00134 | 0.000006 | 0.00001 |
| σ-bond broken/ Å | 3.23 | 4.39 | 4.36 |
| σ-bond formed/ Å | 1.58 | 1.56 | 1.55 |
| C-C-C/degrees | 123.9 | 125.1 | 125.1 |
| Strcture |  |
 |
Intrinsic Reaction Coordinate is a method which involves looking at the geometry structure steps as a reaction proceeds from its TS to the product. This follows a PES curve that has to reach a local minimum. This helps to distinguish which product the 1,5-hexadiene forms. The following are the results from the second method where the force constant is calculated at every step.
 |
 |
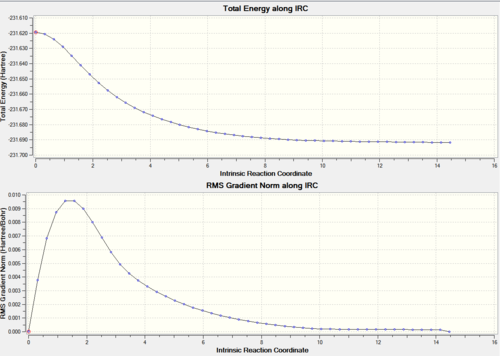Chair IRC: Number of points 50
Force constant only calculated once
Symmetrical so in forward direction
The PES graph illustrates a how the energy is minimised to -231.685a.u.. In order for this to be a minimum the RMS gradient should be zero, but this is not the case. There are 26 intermediate structures. The true lowest energy minimum can be obtained by calculating the force constant in all the steps individually. Other ways include using the end point that the IRC gave for minimisation (might not work if point is far from real min hence not giving the most stable structure) and increasing the number of points (might not work as only 26 should be produced). The use of the previously lowest energy and the introduction of force constants at every step resulted in an improvement in the energy. It was lower in energy by kJmol^-1 compared to the ITC method from before. The energy from the IRC matches the energy of the gauche2 (-231.6917a.u.) which links the chair TS. DOI:10042/to-12511 DOI:10042/to-12512
Boar IRC
The Boat TS can be analysed using the same methods. The same conditions are used for the IRC method to calculate a low energy with a gradient close to zero. An improvement I made in the same way as the chair. Firstly the force constant is calculated at every step and secondly (faster) the last lowest energy obtained from the IRC is taken and used for minimisation. The lowest energy minium is thus obtained. DOI:10042/to-12517
| Method | IRC originally | Optimisation with HF/3-21G basis set | 2nd Optimisation (Force constant calculated at every step) |
| Energy/Hartrees | -231.6719 | -231.6830 | -231.6830 |
| RMS Gradient/a.u. | 0.00091 | 0.000017 | 0.000006 |
| σ-bond broken/ Å | 3.17 | 4.36 | 4.34 |
| σ-bond formed/ Å | 1.61 | 1.58 | 1.58 |
| C-C-C/degrees | 124.1 | 124 | 124 |
| Strcture |  |
 |
 |
 |
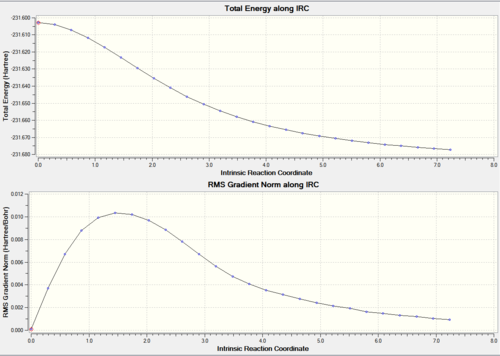Again the trend was the same with 27 intermediates. When convergence occurs a minimum is reached with energy of -231.683 a.u. that doesn’t seem to be like any of the other conformers. This is obtained by optimising the 2nd and 26th IRC structures . The structure is more stable by 0.011a.u. Thios doesn't match the appendix.
Activation energies
Using the TS energy and reactant energy the activation energy can be calculated. This requires a HF/3-21G (DOIs from before) and a DFT-B3LYP method (6-31G* basis set) DOI:10042/to-12518 DOI:10042/to-12519 to analyse the optimisation and frequency of the anti2 reactant species and transition states. The activation energy = transition state energy – anti2 reactant energy. This is done at 0K and 298.15K for the chair and boat respectively.
| HF/3-21G | B3LYP/6-31G(d) | |||||
|---|---|---|---|---|---|---|
| Electronic energy | Sum of zero-point and electronic energies | Sum of thermal and electronic energies | Electronic energy | Sum of zero-point and electronic energies | Sum of thermal and electronic energies | |
| 0 K | 298.15 K | 0 K | 298.15 K | |||
| Chair TS | -231.619 | -231.467 | -231.461 | -234.557 | -234.415 | -234.409 |
| Boat TS | -231.603 | -231.451 | -231.445 | -234.543 | -234.402 | -234.396 |
| Reactant (anti2) | -231.693 | -231.540 | -231.533 | -234.612 | -234.469 | -234.462 |
1 hartree = 627.509kcal/mol
| HF/3-21G | HF/3-21G | B3LYP/6-31G* | B3LYP/6-31G* | Expt. | |
| 0 K | 298.15 K | 0 K | 298.15 K | 0 K | |
| ΔE (Chair) | 45.70 | 44.69 | 34.06 | 33.17 | 33.5 ± 0.5 |
| ΔE (Boat) | 55.60 | 54.75 | 41.96 | 41.32 | 44.7 ± 2.0 |
The chair is more stable than the boat according to the activation energy of both methods so that means that the transition state is a chair for the Cope rearrangement. Although the optimised structures are very alike, the DFT/B3LYP method gave energy values that are lower by approximately 3a.u. The literature values [3] for the activation energy (OK) can be compared to the calculated values of the two methods. The 6-31G* base set using the more complex B3LYP gave energy values closer to the literature making it more accurate (takes into account all the electrons of the system). Further proof for the chair TS is that the reactants had a smaller energy difference with the chair than the boat transition states.
Diels Alder Cycloaddition
The Diels Alder Cycloaddition is a concerted pericyclic reaction where the HOMO and LUMO of two fragments overlap to produce two new molecular orbitals (one bonding and of lower energy and one antibonding). Sigma bonds form between carbon atoms when the dieonophile pi orbitals overlap with the diene pi orbitals. Cyclohexene can be formed by the diels alder reaction between ethylene (dienophile) and cis-butadiene (diene). The HOMO-LUMO overlap can only occur if the FMOs are not asymmetric with respect to each other. A molecular orbital diagram produced from calculating the TS electron density can identify the particular FMO involved in the reaction. There is a vertical sigma plane that goes down and across the single bond of butadiene and the double bond of ethylene and it is existent in both the product and TS. Therefore this is used to examine the symmetries of the orbitals in the C2v cis butadiene and D2h ethylene.
For cis-butadiene the HOMO and LUMO are produced from the overlap of pi orbitals of the two alkenes. In ethylene the HOMO is pi bonding and the LUMO is pi antibonding. This is represented in the diagram.
Reactant Optimisation
 |
 |
 |
 |
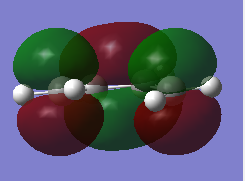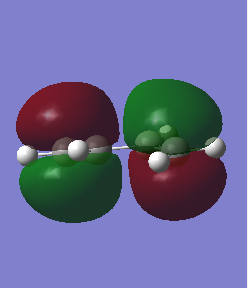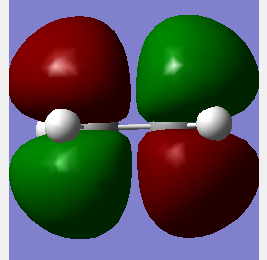The Molecular Orbitals can be solved computationally by solving the Schrodinger equation for electron density hence the symmetry is assigned around the plane previously discussed and the pictorial representation of the orbitals can be seen. The method used was AM1 for both dieonophile and diene discussed earlier. This is a semi-empirical method. The pictorial MOs can then be compared to the qualitative LCAOs and they show a very good agreement. The one difference is that the LCAO approach shows the double bond clouds as two evenly leaning p orbitals. This is incorrect and the computational approach shows them as singular clouds of electrons on both the bottom and top.DOI:10042/to-12520 DOI:10042/to-12521
Optimisation of Transition State
The transition state is investigated in order to show that the butadiene HOMO overlaps with the ethene LUMO and vice versa. The TS structure has to be assumed and drawn manually on gaussview by taking a –CH2-CH2 away from a bicyclic system and changing the single bond to a double along with the addition of 2.2Arsmtrong dashed line bonds ( instead of the full single bonds between the other left over fragments). All this structure changing is because the envelope structure is trying to be achieved for the TS. Then optimisation is performed by freezing the sigma bonds that form and performing a TS(Berny) optimisation (AM1 method) after having the fragment structures minimised. In order to prove that the TS has been reached the geometric structure energy and vibrational analysis calculation are performed.
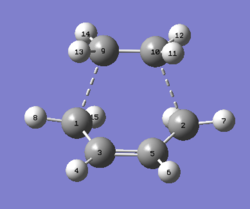
| Parameter | Value |
| Energy/a.u | 0.11165 |
| Gradient/a.u | 0.00003 |
| Fragment separation/Å | 2.17 |
| C1-C3/Å | 1.381 |
| C3=C5/Å | 1.40 |
| C5-C2/Å | 1.381 |
| C9-C10/Å | 1.382 |
| H8-C1-H15/degrees | 115 |
| H4-C3=C5/degrees | 118 |
The lowest energy reached is 0.1117a.u. and this is a minimum as the RMS gradient is converging towards 0. When analysing the structure the sigma bonds between the fragments have a length of 2.119A which is indeed inside the range of the 2 carbon Van der Waals 3.5A radius. This means there is terminal carbon electron density cloud overlap present but the length is a bit too high compared to what it should be (1.3A for C=C). The normal single C-C bonds are shorter than the ideal length and the double bonds is longer than ideal. This is due to the bond forming/breaking. The transition state proposes a sigma to pi transformation which can be shown to be true as the H-C-H angle is 115 which is between a sp2 and sp3 hybridisation model. This is because the bond is eaither formed or broken. Clearly a TS.
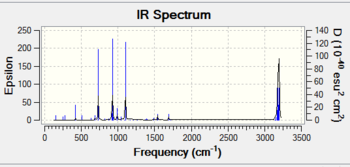
The negative vibration at -955.87cm^-1 is imaginary and due to the FMO overlap. The lowest positive frequency occurs at 147.1cm^-1 for the weakest C-C bond due to the wagging twisting motion of the intermediately forming bond with the cis-butadiene.
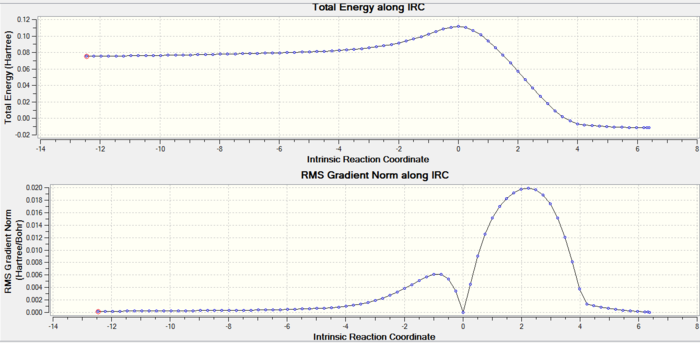
As previously illustrated IRC can model the reaction coordinate along its PES curve. In this case there 50 points and the force constant is calculated at every step, running in the forward and backward directions. Here there are 78 intermediates obtained. The lowest energy product minimum is at the end, the two starting reactants are at the beginning gradually going towards a TS with a RMS gradient decreasing to zero.
| HOMO TS | LUMO TS |
|---|---|
 |
|
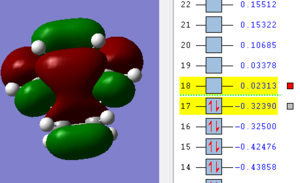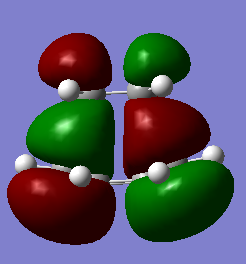
Considering the symmetry along the previously discussed vertical sigma plane the ethene LUMO overlaps with the cis-butadiene HOMO as they are both anti-symmetric. This is the bonding MO with the same symmetry (“a” anti-symmetric). In the anti-bonding MO (symmetric) the HOMO ethene and LUMO cis-butadiene are overlapping (they are both symmetric “s”).
Reaction of cyclohexa-1,3-diene with maleic anhydride
Intoduction
A fascinating regioselective reaction under kinetic conditions is the cycloaddition of maleic anhydride with cyclohexa-1,3-diene. This is a form of Diels Alder reaction. The transition state of the endo is stabilized by secondary orbital overlap (doesn’t exist in exo) so it forms kinetically faster as it has a lower activation energy even though the exo is more thermodynamically favored. The transition states will be investigated to prove this theory (endo rule).
The AM1 level using the TS(Berny) is used to optimise the frozen sigma bonds formed between the maleic anhydride and cyclohex-1,3-ene fragment terminal carbons. The exo and endo products are formed via rotation of the ring.
Molecular orbitals
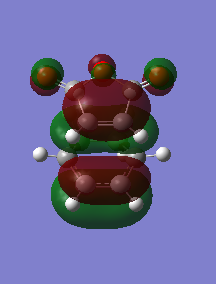
The HOMO and HOMO-1 were looked at closely. The HOMO-1 is formed by a reverse electron demand interaction between the LUMO dienophile and HOMO diene. This is perhaps the source of the secondary overlap shown by the lone pair of oxygen being in the same type of phase as the double bond pi orbital, althought this is not certain. This occurs in the endo TS and not the exo. That was shown by the energy results. On the other hand the normal electron demand interaction of the LUMO and HOMO of the dieonophile and diene forms the HOMO of the TS structure. An interesting result is that in the LUMO+1 from the side view the exo seems to have some type of overlap (maybe secondary) which is unexpected and maybe sterics play an important role as they prevent this overlap. Otherwise the exo would also have the overlap but energy values do not show this. This is a reason the LUMO+1 is not as reliable as the HOMO-1 for the secondary orbital overlap as although there seems to be overlap for the endo (LUMO+1) the exo has some too. DOI:10042/to-12559 DOI:10042/to-12558
| Molecular orbital | HOMO | HOMO-1 |
| Exo |  |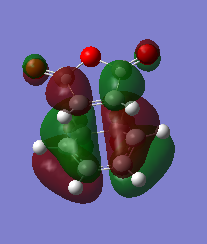
|
| Endo |  |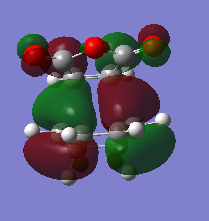
|
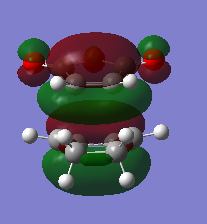
Structural analysis
| Parameter | Endo | Parameter | Exo |
| Energy/a.u | -0.051504 | Energy/a.u | -0.05044 |
| Gradient/a.u | 0.00006772 | Gradient/a.u | 0.000217 |
| Fragment separation/ | 2.15 | Fragment separation/ | 2.17 |
| C9-C17/C12-C15 | 2.73 | C7-C15/C17-C10 | 2.93 |
| C18=C19 | 1.409 | C18=C19 | 1.410 |
| C1=C4 | 1.397 | C1=C4 | 1.396 |
| C1-C2/C3-C4 | 1.383 | C1-C2/C4-C3 | 1.394 |
Exo TS
Endo TS
The energy of the exo is higher by 0.0014a.u. than the endo which confirms that the hypothesis of the endo being kinetically more stable is true. This is because of the secondary orbital overlap and decreased steric hinderance. The structural analysis proves this because the endo carbons for cyclohex-1,3-diene are sp2 which results in less steric repulsion as the through space dashed C-H bonds are longer. On the other hand due to electronic reasons the dashed C-C through space bonds are shorter. For the exo the carbon in the cyclohexa-1,3-diene are sp3 hybridised and have steric repulsions with the carbons on the maleic anhydride. The previously discussed through space dashed carbon-carbon and C-H bonds are shorter. This obviously creates more steric repulsions. This is the reason for the higher energy TS structure.
The electronic reasons discussed before about the exo C-C through space bonds can be analysed by MO. The HOMO of the dienophile can overlap with the diene LUMO as these have the lowest energy between them resulting in a more stable (lower energy) bonding interaction. The AM1 level is used to optimise the TS molecular orbitals for endo and exo. The reason the energy difference is low for that particular HOMO-LUMO interaction is that the dieonophile has an EWG group hence lowering its energy compared to the diene.
IRC
Exo
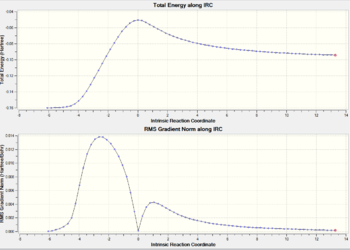
Endo
The IRC method is used on the transition states by using 100points with a force constant calculation at each and every step in both directions. The curves for the endo (76 intermediate geometries) and exo (74 intermediates) are very closely matching. The main difference is the exo isomer has a lower energy for its product yet a higher TS energy. This means the endo has a lower TS energy which proves the kinetic control mentioned. The lower ativation energy makes for a quicker reaction when not much energy is supplied to the system. Under thermodynamic conditions (higher temperature) the exo will dominate.
Conclusion
Transition states occur very quickly and are almost inconceivable to isolate and analyse with normal experiments. This is why computational chemistry is so valuable with its ability to minimise/optimise the different structures to allow energy and structural comparisons. As a result the transition state can be used to predict the most dominant product and explain the reaction mechanism for the Cope and Diels Alder reactions. The transition state in the Cope reaarrangement is the chair conformer (lower energy). The Diels Alder cycloaddition can be further shown by vibrational analysis giving a negative imaginary frequency which is due to FMO. Finally the maleic anhydride reaction is another cycloaddition which has a endo TS under kinetic conditions due to decreased steric repulsions (longer distance) and secondary orbital overlap interactions, although these were not conclusively shown.